利用稳健WTLS方法进行三维激光扫描标靶球定位
王乐洋 陈汉清 林永达 吴华玲
1 东华理工大学测绘工程学院,南昌市广兰大道418号,330013 2 流域生态与地理环境监测国家测绘地理信息局重点实验室,南昌市广兰大道418号,330013 3 江西省数字国土重点实验室,南昌市广兰大道418号,330013
利用稳健WTLS方法进行三维激光扫描标靶球定位
王乐洋1,2,3陈汉清1,2林永达1,2吴华玲1,2,3
1东华理工大学测绘工程学院,南昌市广兰大道418号,3300132流域生态与地理环境监测国家测绘地理信息局重点实验室,南昌市广兰大道418号,3300133江西省数字国土重点实验室,南昌市广兰大道418号,330013
摘要:针对标靶球定位缺少有效的确定协因数阵方法的问题,顾及点到平面的距离反映了点与平面的相关性及入射角对点云数据点位精度的影响,将两者推广到三维激光扫描标靶球定位中。以距离、先验入射角确定各点协因数值,并给出观测向量协因数阵及系数矩阵协因数阵,利用稳健加权总体最小二乘方法进行标靶球定位。实例表明,以距离确定协因数阵的稳健加权总体最小二乘方法解算标靶球参数估计比其他方法更精确。
关键词:标靶球定位; 稳健加权总体最小二乘; 距离; 协因数阵; 异常点
三维激光扫描可快速获取大量点的三维坐标(点云数据)[1]。一般情况下,获取完整的研究对象数据需要从不同视点对物体进行扫描。这其中存在两个问题:一是如何将不同视点的坐标系转换至同一坐标系,即配准问题;二是如何将坐标系转换到常用的地面测量坐标系,即地理参考问题[2]。解决这两个问题的方法之一就是标靶球法。文献[3]提出M-估计的稳健标靶球定位方法,通过剔除或减弱球体数据中异常点对参数估计的影响,获取稳健的标靶球球心坐标。文献[4]提出能同时顾及观测向量误差和系数矩阵误差的总体最小二乘法(TLS)[5]。文献[6]将稳健总体最小二乘法(RTLS)应用于标靶球定位。文献[7]考虑到获取的点云数据是不等精度的,采用加权总体最小二乘方法(WTLS)[8-9]求解标靶球定位问题。文献[10]从点云坐标(x,y,z)的数学表达式出发,在假设水平角和竖直角相等(并作小角度处理)、标靶球各点到仪器中心的距离相等、数据点间独立等精度基础上,得到系数矩阵协因数阵及观测向量协因数阵,利用一种稳健的加权总体最小二乘方法(RWTLS)进行标靶球定位解算。但是,得到的协因数阵仅仅是近似的。
针对上述标靶球定位中协因数阵确定的问题,本文根据点到球面的距离反映了点与球面之间相关性的情况和先验入射角对点云数据点位精度的影响,以这两种方法确定各点协因数值,利用稳健加权总体最小二乘方法进行标靶球定位,并与传统的方法进行比较。
1 RWTLS的标靶球定位方法
1.1RWTLS原理
空间球面方程为:
(1)
式中,r为标靶球半径,(a0,b0,c0)为标靶球球心,(x,y,z)为标靶球所有点观测坐标。式(1)可改写为:
L=Ah
(2)
式中,
(3)
顾及观测向量及系数矩阵均含误差的情况,建立变量含误差(errors-in-variables,EIV)模型:
(4)

(5)
1.2协因数阵的确定方法
1.2.1距离定权
点到球面的距离反映了点与球面之间的相关性[11]。距离越近,相关性就越强,在拟合过程中点的权重也越大。因此,可以把距离作为点的协因数值。点到球面的距离为:
(6)
将各点协因数值控制在[0,1],并将其作为各点协因数的初始值。具体转换公式为[11]:
(7)
式中,di为i点到拟合球面的距离,min(di)为点到拟合球面的距离最小值,max(di)为点到拟合球面的最大值,δ为预设的小值。
1.2.2入射角定权
入射角与点云数据的精度有关。入射角越小,其点位精度越高,即入射角越小,相对应的余弦值越大,因此可把该点的余弦值作为其权值[12-13]。根据空间球面方程的特点,每点协因数值的求解步骤如下。
1)改写空间球面方程式:
F(x,y,z)=(x-a0)2+(y-b0)2+(z-c0)2-r2
(8)
对其求偏导,得到第i点的法向量ni=(2(xi-a0),2(yi-b0),2(zi-c0))。
2)根据i点法向量与i点坐标之间的关系,i点余弦值表达式为:
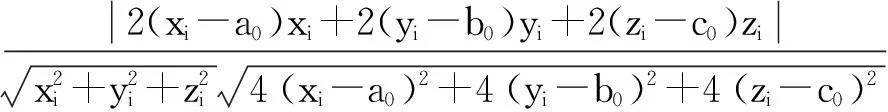
(9)
式中,(xi,yi,zi)为第i点坐标。
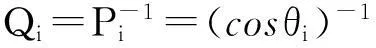
1.2.3观测向量及系数矩阵协因数阵的确定
由空间球面方程知,其系数矩阵A为固定形式。假设点云数据在3个方向为等精度观测,即Qx=Qy=Qz,则根据系数矩阵的特点,并结合文献[14]提出的5条原则,构造系数矩阵A的协因数阵:
(10)
式中,Qx、Qy和Qz分别表示x、y和z的协因数阵。
根据观测向量的特点,且考虑到各点精度不同,构造观测向量的协因数阵,具体步骤如下。

(11)
2)根据协方差传播率,求观测向量协因数阵:
(12)
1.3RWTLS迭代算法
利用文献[15]的WTLS方法,并结合以3倍标准差为阈值剔除异常点,组合成一种RWTLS方法,算法步骤如下。
1)将TLS解作为参数初始解,计算各点初始协因数值,并组合成系数矩阵协因数阵及观测向量协因数阵。
2)计算相关值:

(14)
式中,n为观测值个数。若di<3σ,则保留该点,反之删除。

(15)
(16)
式中,i=1,2,…,n,n为观测点个数。
2 算例分析
利用RIEGLVZ-400三维激光扫描仪同时对均质性良好、表面较为平滑的3个半径分别为5.3cm、7.1cm和10cm的地球仪模型进行扫描。通过抽稀剔除冗余数据,获得3组原始点云数据(如图1)。分别利用RWTLS、WTLS、TLS、LS方法对获得的点云数据进行标靶球拟合,计算单位权中误差、球面拟合精度,并作为评判平差方法优劣的标准。
从表1可以看出,RWTLS方法与WTLS、TLS和LS方法拟合的球半径与厂商设计半径较为接近。以标靶球1为例,RWLTS方法的单位权中误差比WTLS、TLS和LS改善较为明显;3种不同方式确定协因数阵的RWTLS方法中,以距离确定协因数阵的RWTLS方法拟合效果要好,且单位权中误差分别比WTLS、TLS和LS方法提高了100%、99.8%和100%。在球面拟合精度方面,RWTLS方法同样比WTLS、TLS和LS更优;3种RWTLS方法中,以距离确定协因数阵的RWTLS方法球面拟合精度比其他两种RWTLS方法皆减少了一个数量级,且比WTLS、TLS和LS减少了99.8%。TLS方法比WTLS方法的拟合效果好,原因是由于点云数据中存在异常点,以先验信息确定的协因数阵与实际的协因数阵存在偏差,导致WTLS方法解算的参数解可信度降低。而RWTLS自适应地调整协因数阵,使其更接近实际情况,从而获得较为可靠的参数解。

图1 原始标靶球点云数据Fig.1 Point clouds data of tellurion
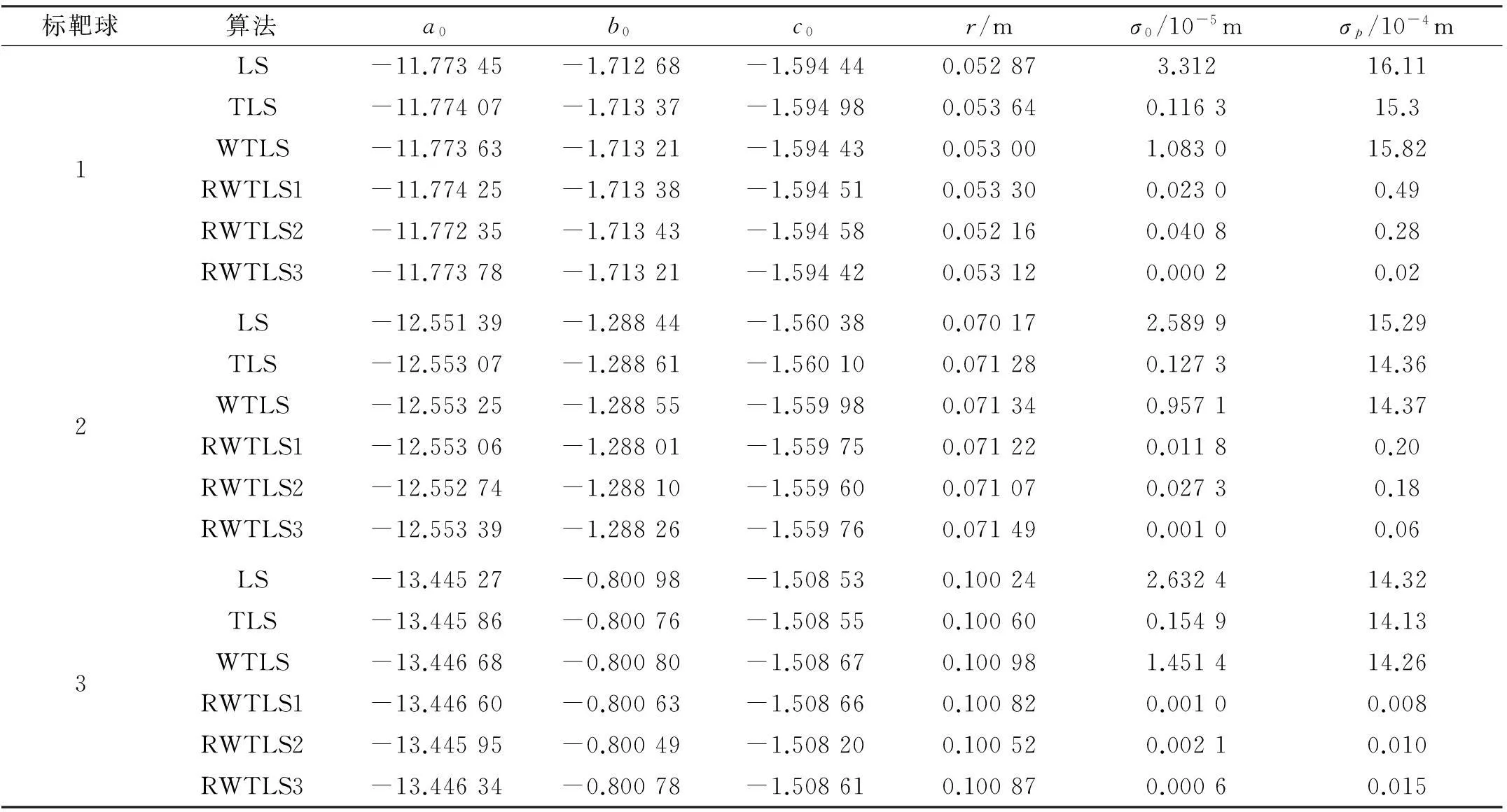
标靶球算法a0b0c0r/mσ0/10-5mσp/10-4m1LS-11.77345-1.71268-1.594440.052873.31216.11TLS-11.77407-1.71337-1.594980.053640.116315.3WTLS-11.77363-1.71321-1.594430.053001.083015.82RWTLS1-11.77425-1.71338-1.594510.053300.02300.49RWTLS2-11.77235-1.71343-1.594580.052160.04080.28RWTLS3-11.77378-1.71321-1.594420.053120.00020.022LS-12.55139-1.28844-1.560380.070172.589915.29TLS-12.55307-1.28861-1.560100.071280.127314.36WTLS-12.55325-1.28855-1.559980.071340.957114.37RWTLS1-12.55306-1.28801-1.559750.071220.01180.20RWTLS2-12.55274-1.28810-1.559600.071070.02730.18RWTLS3-12.55339-1.28826-1.559760.071490.00100.063LS-13.44527-0.80098-1.508530.100242.632414.32TLS-13.44586-0.80076-1.508550.100600.154914.13WTLS-13.44668-0.80080-1.508670.100981.451414.26RWTLS1-13.44660-0.80063-1.508660.100820.00100.008RWTLS2-13.44595-0.80049-1.508200.100520.00210.010RWTLS3-13.44634-0.80078-1.508610.100870.00060.015
注:RWTLS1表示文献[7]的稳健加权总体最小二乘方法;RWTLS2表示以入射角确定协因数阵的稳健加权总体最小二乘方法;RWTLS3表示以距离确定协因数阵的稳健加权总体最小二乘方法。
3 结 语
1)由于获取的点云数据是不等精度的,且带有随机误差和存在异常点,采用LS、TLS和WTLS方法得到的参数解并非最优解。RWTLS方法同时顾及点云数据的这3种情况,解算过程中自适应地调整协因数阵,使协因数阵更接近实际,获得了较为精确的标靶球参数解。
2)因为点到球面之间的距离反映了点与球面的相关性,以距离确定的协因数阵更接近实际,利用距离确定协因数阵的RWTLS方法比其他两种确定协因数阵的RWTLS方法在标靶球定位中能得到更好的效果。
3)针对点云数据存在异常点的问题,更为有效的剔除异常点的方法还需进一步研究。
参考文献
[1]陈汉清, 王乐洋. 点云数据平面拟合的加权总体最小二乘方法[J]. 工程勘察, 2015, 43(11): 59-63(Chen Hanqing, Wang Leyang. Plane Fitting of Poing Clouds Using Weighted Total Least Squares Method[J]. Geotechnical Investigation Surveying,2015, 43(11): 59-63)
[2]李清泉, 杨必胜, 史文中, 等. 三维空间数据的实时获取、建模与可视化[M]. 武汉: 武汉大学出版社, 2003(Li Qingquan, Yang Bisheng, Shi Wenzhong, et al. Real Time Acquisition, Modeling and Visualization of 3D Spatial Data[M]. Wuhan: Wuhan University Press, 2003)
[3]官云兰, 詹新武, 程效军, 等. 一种稳健的地面激光扫描标靶球定位方法[J]. 工程勘察,2008(10): 42-45(Guan Yunlan, Zhan Xinwu, Cheng Xiaojun, et al. Spherical Target Positioning of 3D Laser Scanning Based on a Robust Method[J]. Geotechnical Investigation Surveying, 2008(10): 42-45)
[4]Golub G H, Loan C F. An Analysis of Total Least Squares Problem[J].SIAM Journal on Numerical Analysis, 1980, 17(6): 883-893
[5]王乐洋, 鲁铁定. 总体最小二乘平差法的误差传播定律[J]. 大地测量与地球动力学, 2014, 34(2): 55-59(Wang Leyang, Lu Tieding. Propagation Law of Errors in Total Least Squares Adjustment[J]. Journal of Geodesy and Geodynamics, 2014, 34(2): 55-59)
[6]鲁铁定, 周世健, 张立亭, 等. 基于整体最小二乘的地面激光扫描标靶球定位方法[J]. 大地测量与地球动力学, 2009, 29(4): 102-105(Lu Tieding, Zhou Shijian, Zhang Liting, et al. Sphere Target Fixing of Point Cloud Data Based on TLS[J]. Journal of Geodesy and Geodynamics, 2009, 29(4): 102-105)
[7]陈玮娴, 陈义, 袁庆, 等. 加权总体最小二乘在三维激光标靶拟合中的应用[J]. 大地测量与地球动力学, 2010, 30(5): 90-96(Chen Weixian, Chen Yi, Yuan Qing, et al. Application of Weighted Total Least Squares to Target Fitting of Three-Dimensional Laser Scanning[J].Journal of Geodesy and Geodynamics, 2010, 30(5): 90-96)
[8]许光煜, 王乐洋. 加权总体最小二乘平差方法的比较与分析[J]. 工程勘察, 2014,42(6): 67-72(Xu Guangyu, Wang Leyang. The Comparison and Analysis of Three Weighted Total Least Squares Methods[J]. Geotechnical Investigation Surveying, 2014,42 (6): 67-72)
[9]王乐洋. 基于总体最小二乘的大地测量反演理论及应用研究[J]. 测绘学报, 2012, 41(4): 629(Wang Leyang. Research on Theory and Application of Total Least Squares in Geodetic Inversion[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 629)
[10] 袁豹, 岳东杰, 赵元忆, 等. 基于稳健加权总体最小二乘法的地面三维激光扫描球型标靶定位[J]. 勘察科学技术, 2013(1): 19-22(Yuan Bao, Yue Dongjie, Zhao Yuanyi, et al. Spherical Target Positioning of Terrestrial 3D Laser Scanning Based on Robust Weighted Total Least Squares Method[J]. Site Investigation Science and Technology, 2013(1): 19-22)
[11] 李明峰, 欧江霞, 檀丁, 等. 加权总体最小二乘点云平面拟合定权方法探讨[J]. 大地测量与地球动力学, 2015, 35(3): 428-432(Li Mingfeng, Ou Jiangxia, Tan Ding, et al. Study on Fixed Weighted Methods in Plane Fitting of Point Clouds Based on Weighted Total Least Squares[J]. Journal of Geodesy and Geodynamics, 2015, 35(3): 428-432)
[12] 苍桂华, 李明峰, 岳建平. 以入射角定权的点云数据加权总体最小二乘平面拟合研究[J]. 大地测量与地球动力学, 2014, 34(3): 95-99(Cang Guihua, Li Mingfeng, Yue Jianping. Study on Point Clouds Plane Fitting with Weighted Total Least Squares Based on Incidence Angle Weighting[J]. Journal of Geodesy and Geodynamics, 2014, 34(3): 95-99)
[13] Soudarissanane S, Lindenbergh R, Menmenti M, et al. Scanning Geometry: Influencing Factor on the Quality of Terrestrial Laser Scanning Points[J]. ISPRS Journal of Photogrammertry and Remote Sensing, 2011, 66(4): 389-399[14] Mahboub V. On Weighted Total Least-squares for Geodetic Transformations[J]. Journal of Geodesy, 2012, 86(5): 359-367
[15] Jazaeri S, Amiri-Simkooei A R, Sharifi M A. Iterative Algorithm for Weighted Total Least Squares Adjustment[J]. Survey Review, 2014, 46(334): 19-27
Foundation support:National Natural Science Foundation of China, No. 41204003; Public Benefit Research Foundation (Surveying,Mapping and Geoinformation), No.201512026; Science and Technology Project of the Education Department of Jiangxi Province, No. GJJ150595, KJLD12077, KJLD14049; Fund of Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASMG,No.WE2015005; Fund of Key Laboratory of Mapping from Space, NASMG, No.K201502; Scientific Research Foundation of ECIT, No.DHBK201113; Innovation Fund Designated for Graduate Students of Jiangxi Province, No. YC2015-S266,YC2015-S267; Innovation Fund Designated for Graduate Students of ECIT, No. DHYC-2015005.
About the first author:WANG Leyang, PhD, associate professor, majors in geodetic inversion and geodetic data processing, E-mail: wleyang@163.com.
收稿日期:2015-11-19
第一作者简介:王乐洋,博士,副教授,主要研究方向为大地测量反演及大地测量数据处理,E-mail: wleyang@163.com。
DOI:10.14075/j.jgg.2016.08.020
文章编号:1671-5942(2016)08-0745-05
中图分类号:P207
文献标识码:A
Spherical Target Positioning of 3D Laser Scanning by Using Robust WTLS Method
WANGLeyang1,2,3CHENHanqing1,2LINYongda1,2WUHualing1,2,3
1Faculty of Geomatics, East China University of Technology,418 Guanglan Road, Nanchang 330013,China2Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASMG,418 Guanglan Road, Nanchang 330013, China3Jiangxi Province Key Laboratory for Digital Land, 418 Guanglan Road, Nanchang 330013, China
Abstract:We are concerned with the issue of lacking an effective method to determine the covariance matrix of coefficient matrix and observation vector in spherical target positioning. The distance from point to plane reflects the correlation of point and plane, and the incidence angle makes a difference to point clouds. We expand both of them to spherical target positioning. The covariance matrix of coefficient matrix and observation vector are provided. The robust weighted total least squares method is applied to spherical target positioning, which is based on weighted total least squares and setting certain criteria. Point clouds with outliers are conquered in this method. The experimental results show that robust weighted total least squares, which determined covariance by distance, is better than other methods in spherical target positioning.
Key words:spherical target positioning; robust WTLS; distance; covariance matrix; outliers
项目来源:国家自然科学基金(41204003);测绘地理信息公益性行业科研专项(201512026);江西省教育厅科技项目(GJJ150595,KJLD12077,KJLD14049);流域生态与地理环境监测国家测绘地理信息局重点实验室基金(WE2015005);对地观测技术国家测绘地理信息局重点实验室基金(K201502);东华理工大学博士科研启动基金(DHBK201113);江西省研究生创新专项基金(YC2015-S266,YC2015-S267);东华理工大学研究生创新专项基金(DHYC-2015005) 。

