复数域与实数域最小二乘平差的等价性研究
刘志平 李思达
1 中国矿业大学国土环境与灾害监测国家测绘地理信息局重点实验室, 徐州市大学路1号, 221116
复数域与实数域最小二乘平差的等价性研究
刘志平1李思达1
1中国矿业大学国土环境与灾害监测国家测绘地理信息局重点实验室, 徐州市大学路1号, 221116
摘要:针对等精度独立观测条件下的同一平差问题,从理论上证明复数域与实数域最小二乘平差结果的等价性,并指出复平差方法在函数模型表达上的简便特点。基于常用的图像几何校正多项式模型构造复数域多项式模型,并设计一阶和二阶多项式图像校正算例。结果表明,两种方法的平差结果完全相同,但复数域平差方法的参数维数和法矩阵阶数仅为实数域平差方法的一半。
关键词:实最小二乘平差; 复矩阵求逆; 复最小二乘平差; 等价性; 图像几何校正
实数域最小二乘平差在函数模型及随机模型估计方面已形成较完善的理论体系[1-4],并向复数域测量数据处理理论与方法拓展。有学者[5-10]认为,复数域最小二乘平差精度要高于实数域;也有学者[11]认为,两种平差方法具有相同的参数估计精度。但两种方法的理论关系目前未见报道。本文从理论上研究复数域与实数域最小二乘平差方法的等价性,并将复数域最小二乘平差方法引入图像几何校正[12-14],进一步从应用角度探讨复数域与实数域最小二乘方法的等价性与差异性。
1 复数域最小二乘平差方法
1.1复矩阵求逆方法
将n阶复矩阵A*(本文约定带上标*的为复矩阵)表示为:
(1)
式中,ARe、AIm均为n阶实数矩阵,分别表示复矩阵的实部和虚部;下标Re、Im分别表示向量或矩阵的实部和虚部。设A*的逆为B*,则:
(2)

(3)
进一步,可得3种情况下的复矩阵求逆公式。
1)当ARe可逆、AIm不可逆:
(4)
2)当AIm可逆、ARe不可逆:
(5)
3)当ARe、AIm均可逆:
(6)
1.2复数域平差方法
设复平差模型为:
(7)
式中,B*为已知的复数列满秩矩阵,X*为待求的复参数,L*为观测值复向量,V*为残差复向量。误差方程个数为n,待估参数个数为u,自由度r=n-u。复数域最小二乘平差准则为[1]:
(8)
式中,上标H表示共轭转置。复数域最小二乘的参数估计[5,9]及其方差阵估计分别为:
(9)
(10)

根据式(4)对式(9)、(10)展开,可得复参数及其方差-协方差阵的另一种表达式:
(11)
(12)
式中,
(13)
1.3与实数域方法的理论关系
令式(7)两端实部、虚部分别相等,则可将复数域模型表示为实数域平差模型:
(14)
此时,实数域最小二乘平差准则可表示为:
(15)
基于式(15),可导出实数域参数及其方差-协方差阵的最小二乘估计分别为:
(16)
(17)
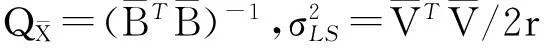
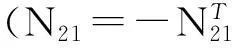
(18)
(19)
对比分析式(11)与式(18)发现,两种方法的参数估值之间的确存在如下的理论关系:
(20)

(21)
式中,Iu表示u阶单位矩阵。
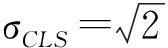
对于u维矩阵,其高斯消去法的计算复杂度[15]为O(u3)。不难发现,对于同一平差问题,复数域平差方法较实数域平差方法其待估模型参数维数、法矩阵阶数均降低了一半,提高了计算效率。
2 图像几何校正及结果分析
遥感图像相对地面目标存在几何畸变,通常利用参考图像或地面控制点进行校正[12]。通常采用实数域的m阶多项式模型:
(22)
式中,(X,Y)表示参考图像的像平面坐标或控制点坐标,(x,y)表示待校正图像的像平面坐标,m表示多项式模型最高阶数,ajk、bjk表示图像几何校正参数。
根据复数运算性质,式(22)可改写为:
(23)
式中,α*jk为复数域参数,且有α*jk=ajk+ibjk。
对比式(22)与式(23)可知,复数模型的方程个数比实数域少了一半,参数维数也少了一半。因此,复数域的模型表达比实数域更简便高效。
当m=1时,可将实数域6参数简化为复数域3参数的一阶多项式模型:
(24)
式中,α*00=a00+ib00,α*10=a10+ib10,α*01=a01+ib01为待求复参数。其中,α*00包含图像平移信息,α*10、α*01包含图像比例尺和旋转信息。
当m=2时,可将实数域12参数简化为复数域6参数的二阶多项式模型:
(25)
式中,α*00、α*10、α*01含义同上,α*11、α*20、α*02包含图像偏扭、弯曲等信息。
算例1采用经一阶多项式模型转换前后的两幅近景摄影图像,从中选取46对同名点坐标,分别进行实数域和复数域最小二乘平差(先验权阵取单位阵)计算。设计方案为:方案1-A,采用实数域最小二乘平差方法进行参数及中误差估计;方案1-B,采用复数域最小二乘平差方法进行参数及中误差计算,结果见表1。
算例2采用二阶多项式模型对某遥感影像进行几何校正(图像空间分辨率为5 m)。选取均匀分布的24个地面控制点(坐标误差可忽略),分别进行实数域和复数域多项式几何校正模型参数估计。设计方案为:方案2-A,对控制点二维坐标加入随机误差e~N(0,52),分别采用复、实数域平差方法进行二阶多项式模型参数及中误差计算;方案2-B,对控制点二维坐标加入随机误差e~N(0,0.52),分别采用复、实数域平差方法进行二阶多项式模型参数及中误差计算,结果见表2。

表1 算例1不同方案的平差结果

表2 算例2不同方案的平差结果
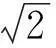
3 结 语
对于独立等精度观测条件下的同一个最小二乘平差问题,实数域方法与复数域方法是等价的。同时,复数域平差较实数域平差的参数维数减少一半、法矩阵阶数减少一半,从而提高了计算效率。实例表明,可将实数域平差问题转换到复数域处理,以简化平差模型并成倍缩短计算时间。但是,在实际测量中并不一定满足独立等精度观测条件。因此,为建立完善的复数域最小二乘参数估计和精度评定理论,需进一步探究相关观测值的复最小二乘平差方法。
参考文献
[1]崔希璋, 於宗俦, 陶本藻, 等. 广义测量平差[M]. 武汉: 武汉大学出版社, 2005 (Cui Xizhang, Yu Zongchou, Tao Benzao, et al. Generalized Surveying Adjustment[M]. Wuhan: Wuhan University Press, 2005)
[2]朱建军, 田玉淼, 陶肖静. 带准则参数的平差准则及其统一与解算[J]. 测绘学报, 2012, 41(1):8-13(Zhu Jianjun, Tian Yumiao, Tao Xiaojing. United Expression and Solution of Adjustment Criteria with Parameters[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1):8-13)
[3]刘志平. 等价条件闭合差的方差-协方差分量估计解析法[J]. 测绘学报, 2013, 42(5): 648-653(Liu Zhiping. Analytical Method for VCE Using Equivalent Condition Misclosure[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 648-653)
[4]刘志平, 张书毕. 方差-协方差分量估计的概括平差因子法[J]. 武汉大学学报:信息科学版, 2013, 38(8): 925-929(Liu Zhiping,Zhang Shubi. Variance-Covariance Component Estimation Method Based on Generalization Adjustment Factor[J]. Geomatics and Information Science of Wuhan University, 2013, 38(8): 925-929)
[5]谷湘潜, 康红文, 曹鸿兴. 复数域内的最小二乘法[J]. 自然科学进展, 2006, 16(1): 49-54(Gu Xiangqian, Kang Hongwen, Cao Hongxing. The Least-Square Method in Complex Number Domain[J]. Progress in Natural Science, 2006, 16(1): 49-54)
[6]谷湘潜, 康红文, 江剑民, 等.用复数自回归模式预报月平均气温[J].应用气象学报,2007,18(4):435-440(Gu Xiangqian,Kang Hongwen,Jiang Jianmin. Monthly Temperature Forecasts by Using a Complex Autoregressive Model[J]. Journal of Applied Meteorological Science, 2007, 18(4): 435-440)
[7]董勇, 李梦霞. 复数域内最小二乘法估计公式的证明[J]. 长江大学学报:自然科学版,2007,4(2): 129-130 (Dong Yong, Li Mengxia. The Prove to the Formula of Complex Least Squares[J]. Journal of Yangtze University:Natural Science Edition, 2007, 4(2): 129-130)
[8]李梦霞, 陈忠. 复数域内最小二乘法的一种改进[J]. 长江大学学报:自然科学版, 2008, 5(3): 7-8(Li Mengxia, Chen Zhong. The Modification of Least Square Method(LSM) in the Complex Field[J]. Journal of Yangtze University: Natural Science Edition, 2008, 5(3): 7-8)
[9]朱建军, 解清华, 左廷英, 等. 复数域最小二乘平差及其在POLInSAR植被高反演中的应用[J]. 测绘学报, 2014, 43(1): 45-51(Zhu Jianjun, Xie Qinghua, Zuo Tingying, et al. Complex Least Square Adjustment and Its Application in Tree Height Inversion with POLInSAR Data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 45-51)
[10] Fu H Q, Wang C C, Zhu J J, et al. Inversion of Vegetation Height from POLInSAR Using Complex Least Squares Adjustment Method[J]. Science China:Earth Sciences,2015, 58 (6): 1 018-1 031
[11] Zeng H E. Planar Coordinate Transformation and Its Parameter Estimation in the Complex Number Field[J]. Acta Geod Geophys, 2014, 49(1):79-94
[12] 张连蓬, 陶华学, 刘国林, 等. 遥感图像几何校正的非线性有理逼近模型[J]. 煤炭学报, 2003, 28(2): 140-144(Zhang Lianpeng, Tao Huaxue, Liu Guolin, et al. The Model of Nonlinear Rational Approximation for Geometric Correction of Remote-Sensing Image[J]. Journal of China Coal Society, 2003, 28(2): 140-144)
[13] 朱述龙, 史文中, 张艳, 等. 线阵推扫式影像近似几何校正算法的精度比较[J]. 遥感学报, 2004, 8(3): 220-226(Zhu Shulong, Shi Wenzhong, Zhang Yan, et al. Precision Comparison of Several Algorithms for Approximate Rectification of Linear Array Push-broom Imagery[J]. Journal of Remote Sensing, 2004, 8(3): 220-226)
[14] 张姣, 李俊山, 杨亚威. 结合仿射变换和多层B样条配准的湍流畸变图像校正[J]. 光学精密工程, 2015, 23(3): 846-854(Zhang Jiao, Li Junshan, Yang Yawei. Turbulence Distorted Image Correction Using Affine Transformation and Multilevel B-Spline Registration[J].Optics and Precision Engineering, 2015, 23(3): 846-854)
[15] 冉瑞生, 黄廷祝. 三对角矩阵的逆[J]. 哈尔滨工业大学学报, 2006, 38(5): 815-817(Ran Ruisheng, Huang Tingzhu. Inverse of Tridiagonal Matrices[J]. Journal of Harbin Institute of Technology, 2006, 38(5): 815-817)
Foundation support:National Natural Science Foundation of China, No. 41204011,41504032; Open Fund of State Key Laboratory of Geodesy and Earth’s Dynamics, No. SKLGED2014-3-2-E.
About the first author:LIU Zhiping, associate professor, majors in adjustment theory, navigation positioning and geospatial inversion, E-mail:zhpliu@cumt.edu.cn.
收稿日期:2015-10-08
第一作者简介:刘志平,副教授,主要从事误差理论、导航定位和反演分析研究,E-mail:zhpliu@cumt.edu.cn。
DOI:10.14075/j.jgg.2016.08.019
文章编号:1671-5942(2016)08-0741-04
中图分类号:P207
文献标识码:A
Research on Equivalence between Complex-Valued and Real-Valued Least Squares Adjustment Method
LIUZhiping1LISida1
1Key Laboratory of Land Environment and Disaster Monitoring of NASMG, China University of Mining and Technology,1 Daxue Road, Xuzhou 221116, China
Abstract:Firstly, the inverse formula of complex matrix is provided in this paper, on which the complex-valued least squares adjustment method (CLS) for complex-valued linear model is presented in detail. Then, based on the equivalent adjustment model with independent observations weighted equally, it is proven theoretically that the CLS method is equivalent to the real-valued least squares method (LS). However, the CLS method is greatly superior to the LS method in efficiency. Lastly, both real-valued and complex-valued polynomial models for image geometric correction are employed to verify the validity of the CLS method. Results show that CLS and LS method have no difference in parameter and in accuracy estimation, and the CLS method is very helpful in simplifying the adjustment model and in improving calculation efficiency, because the number of complex-valued parameters is only equal to the half of the number of real-valued parameters.
Key words:real-valued least squares method; complex matrix inversion; complex-valued least squares method; equivalence; image geometric correction
项目来源:国家自然科学基金(41204011, 41504032);大地测量与地球动力学国家重点实验室开放基金(SKLGED2014-3-2-E)。

