一种基于改进TurboEdit的GPS周跳探测与修复方法
党子越 夏凤雨
1 长安大学地质工程与测绘学院,西安市雁塔路126号,710064
一种基于改进TurboEdit的GPS周跳探测与修复方法
党子越1夏凤雨1
1长安大学地质工程与测绘学院,西安市雁塔路126号,710064
摘要:基于TurboEdit算法中的MW组合,利用卡尔曼滤波分离宽巷模糊度以提高模糊度精度。利用移动窗口的多项式拟合对原GF组合中的多项式拟合进行改进,并对周跳的浮点解进行计算。使用GPS数据检测方法的正确性,结果表明,该方法能探测并修复小周跳、大周跳以及多个周跳。
关键词:GPS;周跳;TurboEdit算法;移动窗口;卡尔曼滤波
GPS周跳探测与修复方法[1-5]存在缺陷:高阶差分法不能探测5周以下的小周跳;多项式拟合法在拟合阶数和拟合长度的选择上容易引入人为误差,并且无法探测小周跳;电离层残差法中,当L1和L2频率上发生的周跳为L1和L2的频率之比时,则无法探测出该周跳;TurboEdit法中,窄巷伪距易受多路径效应影响[6],且其中用到的P1码一般无法获取,只能用C/A码代替,但由于C/A码精度较低,会对周跳检测结果产生较大影响。本文对TurboEdit方法进行改进,在MW组合模型中,利用卡尔曼滤波法,在解算多路径误差的同时将宽巷模糊度与多路径误差进行实时分离,得到较为准确的宽巷模糊度;再采用固定弧段长度的移动窗口多项式拟合法对GF组合进行改进,从而实现双频GPS的周跳探测与修复。
1 TurboEdit法周跳探测原理
MW组合整周模糊度为[7]:
(1)
式(1)通过宽巷组合消除了电离层误差、接收机钟差以及卫星钟差,仅剩下模糊度项、多路径误差以及GPS测量噪声,因此该组合在消除多路径误差及测量噪声的前提下适用于周跳的探测与修复。根据文献[7],利用误差传播律计算出先验均方根中误差,然后采用递推公式递推出每一个历元的宽巷模糊度的均值及其均方根中误差。
通过(i+1)历元与i历元的宽巷模糊度之差来判断i历元观测值是否存在周跳:
(2)
根据载波相位、码伪距观测方程可导出无几何距离组合LGF[7-8]:
(3)
对LGF进行多项式拟合,拟合出的结果记为QGF,拟合的阶数为min[(N/100+1),6],N为历元个数。由以下不等式来判断发生周跳的历元:
(4)
若式(4)中两个不等式同时成立,则判断i历元发生周跳。
2 改进的TurboEdit算法
式(5)为含伪距多路径与噪声的宽巷相位减窄巷伪距组合。可以看出,含多路径误差的码观测值对确定宽巷模糊度具有非常大的影响:
(5)
运用宽巷相位减窄巷伪距组合模型求解宽巷模糊度时,需要L1相位上的P1码。但是大多数情况下,P1码不易获取,常常采用C/A码代替P1码。但是C/A码精度较低,不能满足正确求解模糊度的需求,且C/A码极易受伪距多路径误差的影响。因此,在解算模糊度浮点解时,得到的结果精度往往较低。要求解出正确的宽巷模糊度,需要将式(5)中的伪距多路径与宽巷模糊度进行实时分离。根据伪距与时间间隔有一定相关性的特质,对多路径采用一阶高斯-马尔科夫过程建立如下模型[9]:
(6)
不发生周跳时,整周模糊度为常数。因此,可以建立以宽巷模糊度和伪距多路径误差为参数的状态方程:
(7)
将式(7)作为离散系统的观测方程,结合式(5)可列出如下卡尔曼方程:
(8)
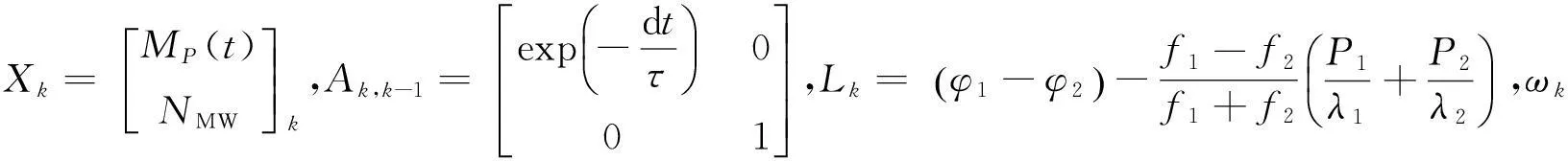
通过滤波公式便可逐历元计算出整周模糊度的浮点解及其对应的方差阵,继而推算出整周模糊度的准确值。
在用TurboEdit方法探测周跳时,GF组合模型中采用多项式拟合法对电离层组合进行拟合。而实际情况中,拟合阶数和拟合长度易受人为影响,若两者不符,则会产生较大的拟合误差,导致周跳探测过程出现问题。本文采用一种基于移动窗口的多项式拟合法[10],对LGF(i)进行拟合。取移动窗口大小为m、拟合阶数为n,则:
(9)
选取当前历元前m个LGF进行多项式拟合。根据式(6)判断当前历元是否发生周跳,若发生周跳,则先对该历元的载波相位观测值进行修复,将新的值赋予LGF(i),窗口向前移动,直到最后一个历元。本文实验数据采用大小为20的窗口,拟合阶数为3,拟合的情况最佳。
3 移动窗口多项式拟合法
探测出周跳后,采用移动窗口的多项式拟合法对L1和L2相位观测值分别进行拟合[11]:
(10)
若已探测出i历元发生周跳,则利用i历元前固定长度的窗口对i历元的L1和L2相位观测值分别进行拟合,通过式(11)计算L1和L2相位分别发生的周跳值:
(11)
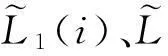
4 实例分析
采用2010年年积日为60d的AMC站观测数据amc20600.10°。该数据包含L1相位、L2相位、C/A码、P1码、P2码,数据采样率为30s。选取PRN32号卫星,截取第1h共240个历元作为观测数据。通过图1的MW组合图形和GF组合图形可看出,该数据不含周跳,图像的不规则波动是由噪声和伪距多路径效应引起的。
通过以下3种方案检验本文方法的正确性。
方案一:在第50个历元分别给(L1,L2)相位加入(9,7)周跳;在第100个历元分别给(L1,L2)相位加入(2,2)周跳;
方案二:在第100个历元分别给(L1,L2)相位加入(-60,-60)周跳,在第200个历元分别给(L1,L2)相位加入(77,60)周跳;
方案三:在第50个历元分别给(L1,L2)相位模拟加入(2,-1)周跳,在第100个历元分别给(L1,L2)相位加入(30,30)周跳;在第150个历元分别给(L1,L2)相位加入(77,60)周跳。
比较图1和图2可明显看出,相比P1码数据,C/A码数据噪声更大。从图3可看出,经过卡尔曼滤波分离后的宽巷模糊度消除了伪距多路径效应和噪声等误差,固定出了一个较为精确的宽巷模糊度。
从图4~6可看出,MW组合对形如(9,7)和(77,60)的特殊比例周跳和(2,-1)这样的小周跳具有探测能力,却对(2,2)、(30,30)和(-60,-60)的等周周跳不敏感;GF组合可探测出(2,2)、(30,30)和(-60,-60)的等周周跳,却对周跳(9,7)和(77,60)不敏感。且无论是MW组合还是GF组合,都对多个周跳具有探测能力。因此,将MW组合和GF组合联合起来探测周跳,可以得到准确的探测结果。
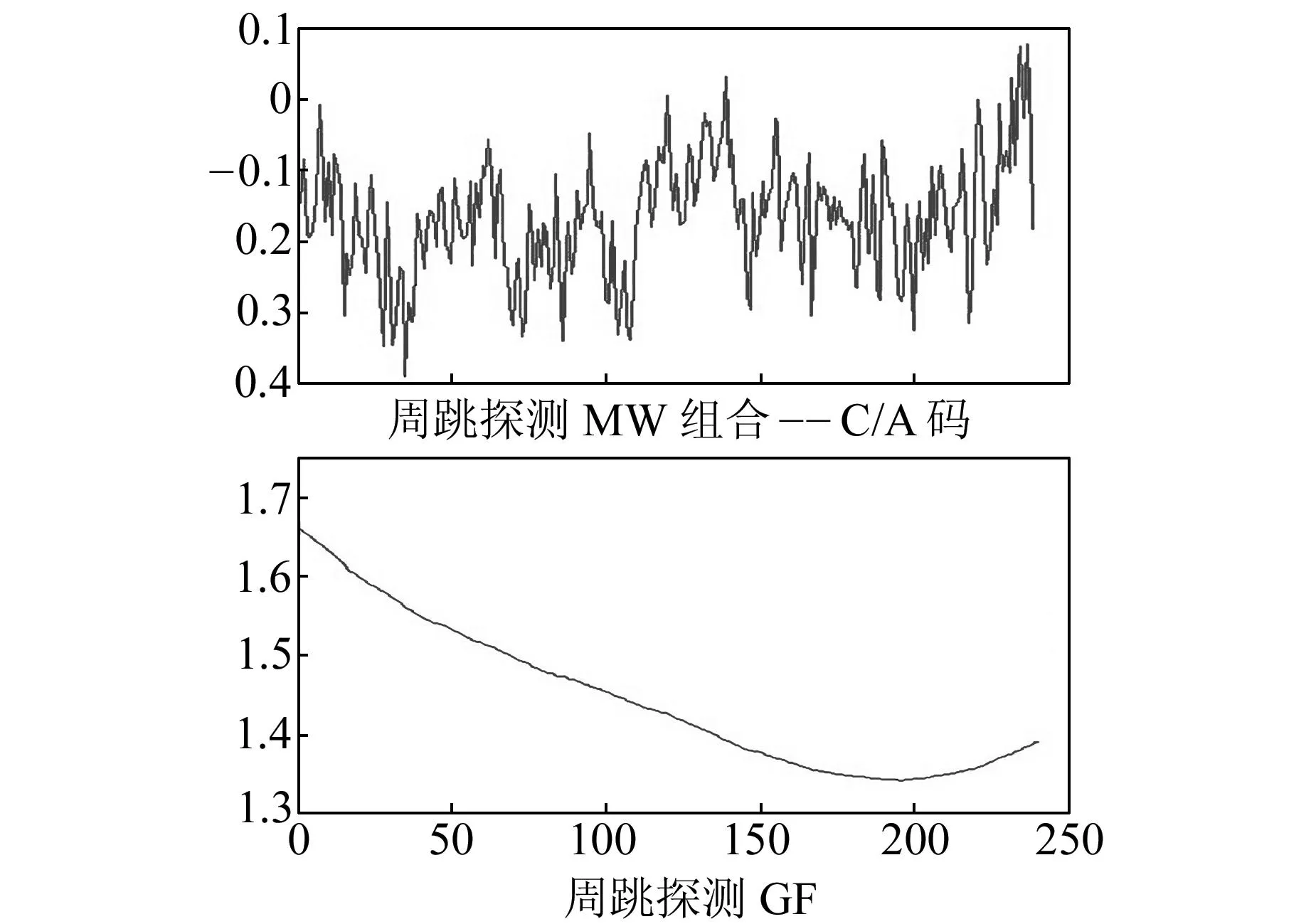
图1 无周跳的MW组合和GF组合Fig.1 MW combination and GF combination without cycle slips
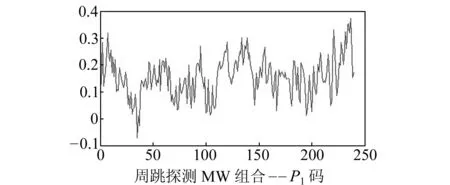
图2 无周跳P1码的模糊度Fig.2 Ambiguity without cycle slips (P1)
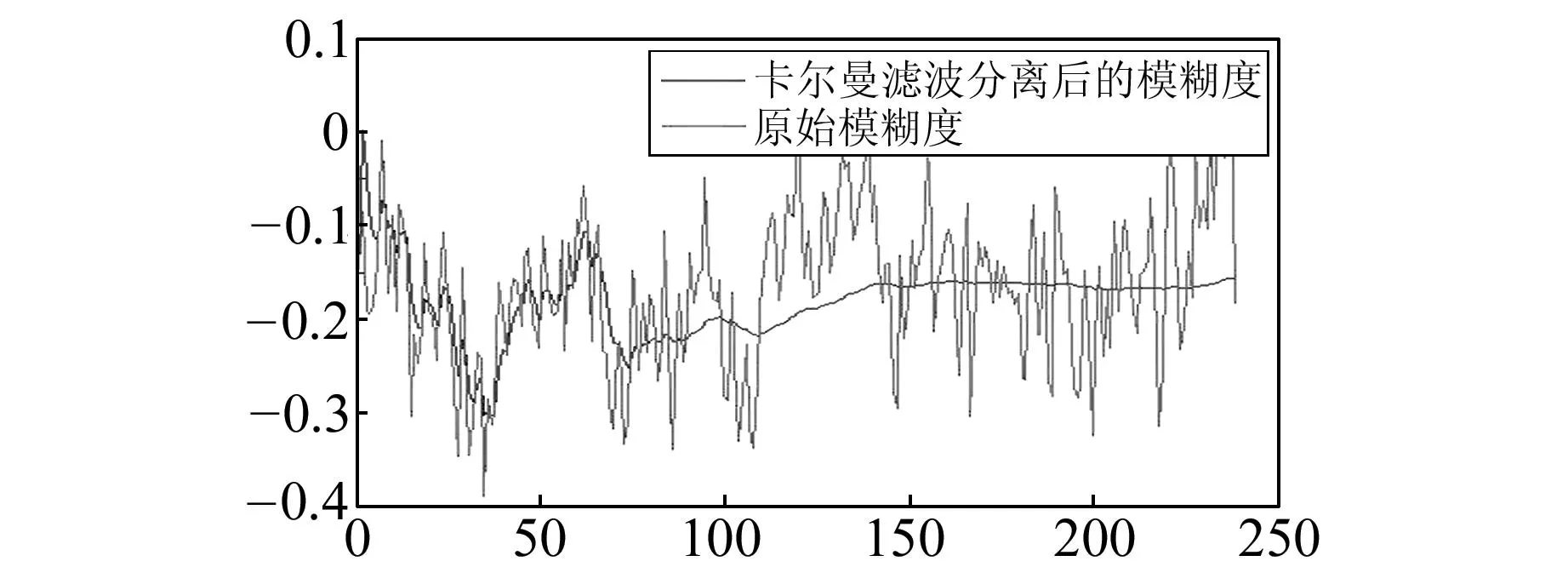
图3 无周跳滤波后与无滤波的模糊度(C/A码)Fig.3 Comparison of filtered and unfiltered ambiguity without cycle slips (C/A)
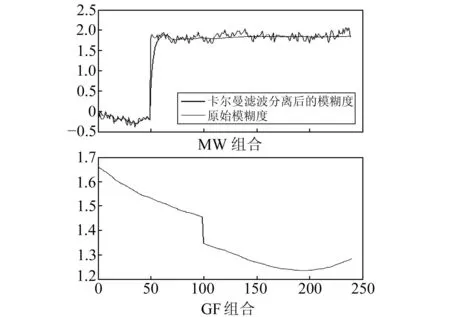
图4 方案一Fig.4 Solution 1
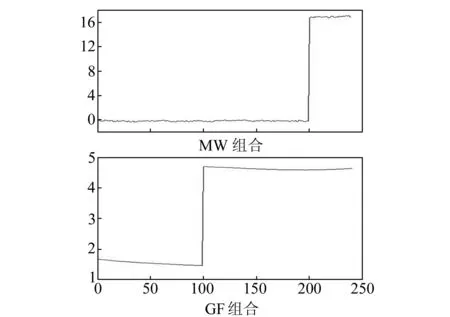
图5 方案二Fig.5 Solution 2
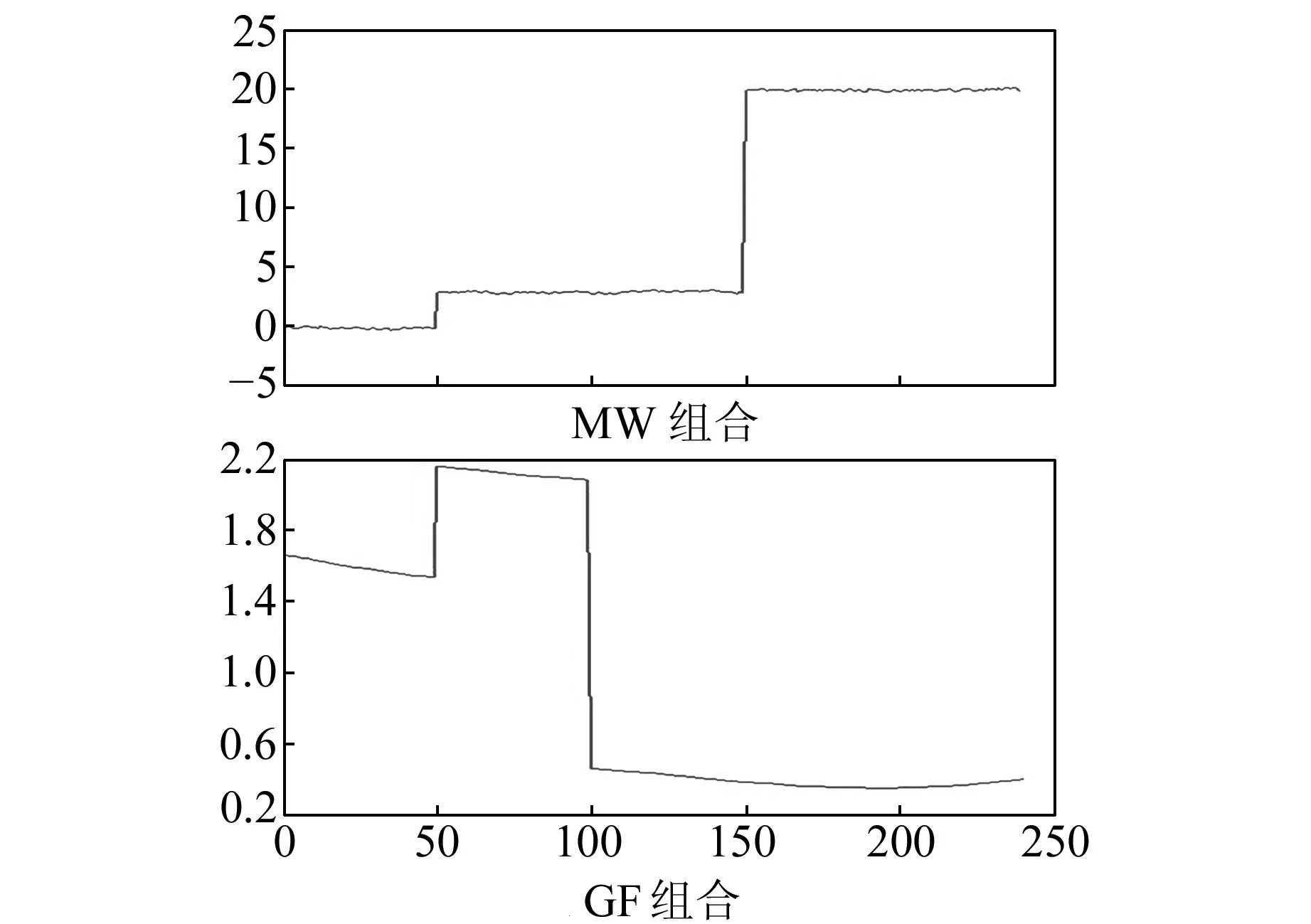
图6 方案三Fig.6 Solution 3
周跳修复时,采用移动窗口的多项式拟合法对上述方案加入的周跳值进行计算,计算结果见表1。
从表1可看出,用移动窗口的多项式拟合法计算周跳时,对于模拟加入的小周跳、大周跳、多个周跳、等值周跳和特殊比例周跳都能够计算出准确的周跳值,得到的周跳浮点解取整后与周跳值完全相等。因此,该方法可以用来计算可靠的周跳值。
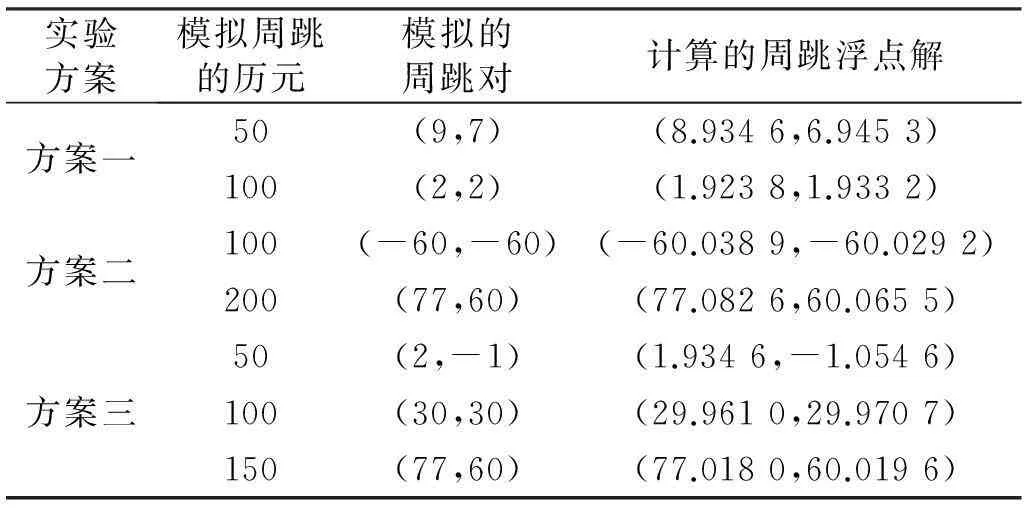
表1 实验模拟添加周跳的方案
5 结 语
本文在TurboEdit方法的基础上,提出一种改进的周跳探测与修复方法。实验证明,本文提出的针对MW组合的卡尔曼滤波法能够提高计算出的整周模糊度的精度,为后续周跳探测打下坚实基础;改进的GF组合中的移动窗口多项式拟合法有效减少了人为选取拟合阶数和拟合长度所产生的误差,较好地探测出周跳发生的位置;周跳修复所采用的移动窗口的多项式拟合法能够精确地计算出周跳的大小。本文所提出的改进方法对小周跳、大周跳以及多个周跳均能较好地探测并修复。
参考文献
[1]冯磊.GPS周跳探测与修复的方法研究[D].阜新:辽宁工程技术大学,2011(Feng Lei.Research on the Method of GPS Cycle Slip Detection and Restoration[D].Fuxin:Liaoning Technical University,2011)
[2]Lichtenegger H, Hofmann-Wellenhof B. GPS Data Preprocessing for Cycle-Slip Detection[C].Global Positioning System: An Overview, Edinburgh,1989
[3]Mader G L.Dynamic Positioning Using GPS Carrier Phase Measurements[J].Manuscripta Geodaetica,1986,17(4):272-277
[4]Goad C.Precise Positioning with the Global Positioning System[C]. The Third International Symposium on Inertial Technology for Surveying and Geodesy, Baff, 1985
[5]Blewitt G.An Automatic Editing Algorithm for GPS Data[J].Geophysical Research Letters,1990,17(3):199-202
[6]张孟阳,吕保维,宋文淼.GPS系统中的多径效应分析[J].电子学报,1998,26(3):10-14(Zhang Mengyang,Lü Baowei, Song Wenmiao. Analyses of Multipath Effects in the GPS System[J].Acta Electronica Sinica,1998,26(3):10-14)
[7]郑作亚,程宗颐,黄珹,等.对Blewitt周跳探测与修复方法的改进[J].天文学报,2005,46(2):216-224(Zheng Zuoya, Cheng Zongyi, Huang Cheng, et al. Improving of Cycle-slip Detection and Correction of Blewitt Method[J].Acta Astronomica Sinica,2005,46(2):216-224)
[8]王敬,赵军祥.Blewitt周跳探测方法的改进[J].飞行器测控学报,2011,30(2):80-83(Wang Jing, Zhao Junxiang.An Improvement of Blewitt Cycle Slip Detection[J].Journal of Spacecraft TT&C Technology,2011,30(2):80-83)
[9]范建军,雍少为,王飞雪.基于卡尔曼滤波的多径误差消除及双频模糊度快速估计方法研究[J].电子与信息学报,2008,30(5):1 075-1 079(Fan Jianjun, Yong Shaowei, Wang Feixue. Study on Multipath Mitigation and Dual-Frequency Fast Ambiguity Estimation Based on Kalman Filter[J].Journal of Electronics and Information Technology, 2008, 30(5): 1 075- 1 079)
[10]李明,高星伟,徐爱功.一种改进的周跳多项式拟合方法[J].测绘科学,2008,33(4):37-38(Li Ming,Gao Xingwei, Xu Aigong. A Modified Polynomial Fitting of Cycle-slip Processing[J].Science of Surveying and Mapping,2008,33(4):37-38)
[11]石双忠,冯尊德.利用多项式拟合预测残差修正法估算周跳值[J].测绘科学,2013,38(1):33-35(Shi Shuangzhong, Feng Zunde.Estimation of GPS Cycle Slips Value Corrected by Predicted Residual of Polynomial Fitting[J].Science of Surveying and Mapping,2013,38(1):33-35)
About the first author:DANG Ziyue,majors in surveying engineering, E-mail: caesarah1112@gmail.com.
收稿日期:2015-08-19
第一作者简介:党子越,主要从事测绘工程研究,E-mail: caesarah1112@gmail.com。
DOI:10.14075/j.jgg.2016.08.015
文章编号:1671-5942(2016)08-0723-04
中图分类号:P228
文献标识码:A
An Improved Detection and Repair Method for Cycle Slips Based on TurboEdit Algorithm
DANGZiyue1XIAFengyu1
1School of Geology Engineering and Geomatics, Chang’an University, 126 Yanta Road, Xi’an 710064,China
Abstract:This method is an improvement based on TurboEdit algorithm. Firstly, it uses the Kalman filter to separate the ambiguity resolution in order to improve the precision of the ambiguity, thus to set up the foundation for detecting the repairing the cycle slips properly; Secondly, this method uses a fixed length sliding window fitting model to improve the polynomial fitting of the original GF combination; Thirdly, it uses the fixed length sliding window fitting model to calculate the floating solution of the cycle slips while repairing the cycle slips. The validity of this method has been tested by the GPS data. The results show that this method is valid for the detection and repair for small, big and multiple cycle slips.
Key words:GPS; cycle slips; TurboEdit algorithm; sliding window; Kalman filter algorithm

