利用SLR检核GOCE卫星精密轨道

衷路萍　邹贤才　吴林冲　于　男

1　武汉大学测绘学院，武汉市珞喻路129号，430079



利用SLR检核GOCE卫星精密轨道

衷路萍1邹贤才1吴林冲1于男1

1武汉大学测绘学院，武汉市珞喻路129号，430079

摘要：采用2009-11-01～2010-01-31三个月的SLR观测数据，对GOCE卫星运动学轨道 PKI(precise kinematic orbit)进行检核。基于残差分析发现，SLR观测存在测站时距系统性偏差。消除测站时距偏差后，GOCE卫星PKI精密轨道的外符合精度达到1.5 cm。

关键词：精密轨道；卫星激光测距；外部检核；时距偏差

GOCE卫星[1]精密轨道产品包括简化动力学轨道PRD(precise reduced-dynamic orbit)和运动学轨道PKI，均是基于GPS卫星跟踪，其轨道内符合精度为2 cm[2]。GOCE卫星搭载了激光后向反射器，可实施人卫激光测距。目前SLR测距精度为亚cm级，对于一些观测条件好的测站甚至可以达到几mm，成为单次测距精度最高的空间大地测量技术之一[3]。由于SLR的距离观测独立于GPS卫星跟踪，故可利用SLR技术对GOCE卫星精密轨道作外部检核。利用SLR检核卫星轨道实际上就是比较SLR得到的星地距离观测值和通过卫星精密轨道获得的星地距离计算值之间的差异，两个距离较差的统计结果就是卫星轨道精度。

1　方法与模型

1.1SLR检核卫星轨道的方法

SLR技术的原理是观测激光脉冲信号在地面激光发射站与卫星反射器间的传播时间，然后乘以光速，从而转换为地面测站至卫星的距离。其单程距离为:

(1)

式中，ρ为星地距离，c为光速，Δt为激光脉冲信号的双程传播时间。

根据地面测站位置和卫星轨道信息，可以计算地面测站至卫星的距离:

(2)

式中，ρ为星地距离，(xs,ys,zs)为卫星(质心)位置矢量，(xi,yi,zi)为第i个测站(系统参考中心SRP)位置矢量。

利用SLR检核卫星轨道精度的原理就是比较上述星地距离的观测值和计算值之间的差。为区分两个距离，将星地距离观测值记为ρo，计算值记为ρc，两者之差表示为:

(3)

1.2改正模型

由于SLR观测在传播路径和卫星上有各种误差，因此需要对SLR原始距离观测值作数据预处理，包括对流层改正[4]、卫星质心改正[5-6]和广义相对论改正[4]:

(4)

式中，ρatm为对流层延迟改正，ρcom为卫星质心改正，ρrel为广义相对论改正。

卫星位置矢量(xs,ys,zs)根据卫星轨道信息内插得到，而测站位置矢量(xi,yi,zi)则由地面测站系统的ITRF坐标归算至系统参考点SRP(system reference point)，需作的改正包括地壳运动改正、潮汐位移改正[4]和测站偏心改正。各项改正模型如表1所示。

此外，地面测站由于系统设备物理性质、观测条件等各种因素，在观测过程中存在时间和距离上的系统误差[3]，分别为时间偏差Tb和距离偏差Rb。时间偏差指计时器在事件历元的记录时刻提前或延迟了时间Tb，距离偏差指测距误差Rb。在数据后处理分析时，采用时距偏差模型[7-9]估计Tb和Rb两个参数:

(5)

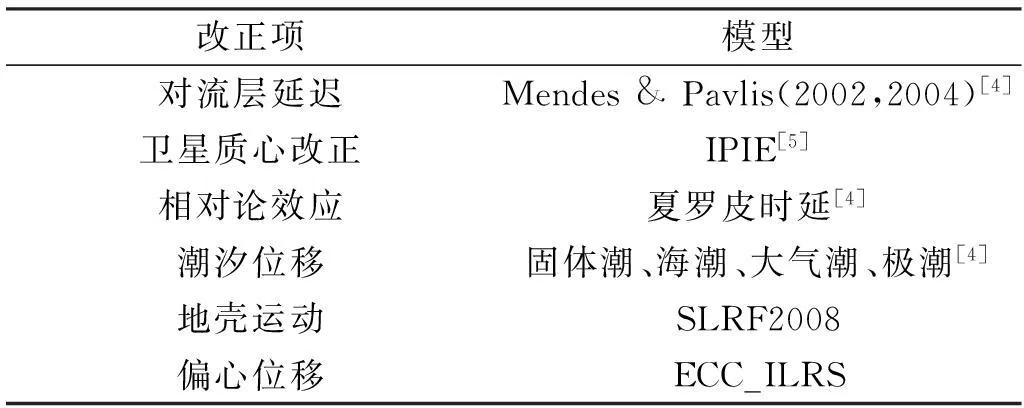
表1　SLR数据处理中各项改正模型

注：IPIE(The Institute of Precision Instruments Engineering)。

2　计算与分析

GOCE卫星轨道数据采用AIUB(Astronomical Institute of the University of Bern)基于GPS跟踪的PKI精密轨道。本文利用2009-11-01～2010-01-31三个月内所有GOCE卫星SLR跟踪的标准点数据，对其轨道作外部检核。由于GOCE卫星轨道较低、运行速度快，SLR跟踪较难实现，每次过境只有几分钟的观测，总观测数据少。在计算时间段内所有的SLR观测统计如图1，全球有20个测站观测，共5 897个标准点数据。由于南北半球测站分布不均匀，南半球只有4个观测站，几何结构较差。且各测站观测能力差异较大，其中南半球Yarragadee(ID: 7090)站观测标准点数近2 000个，占总观测量的1/3，少数几个测站观测标准点数近900个，而大部分测站观测标准点数不足300个。

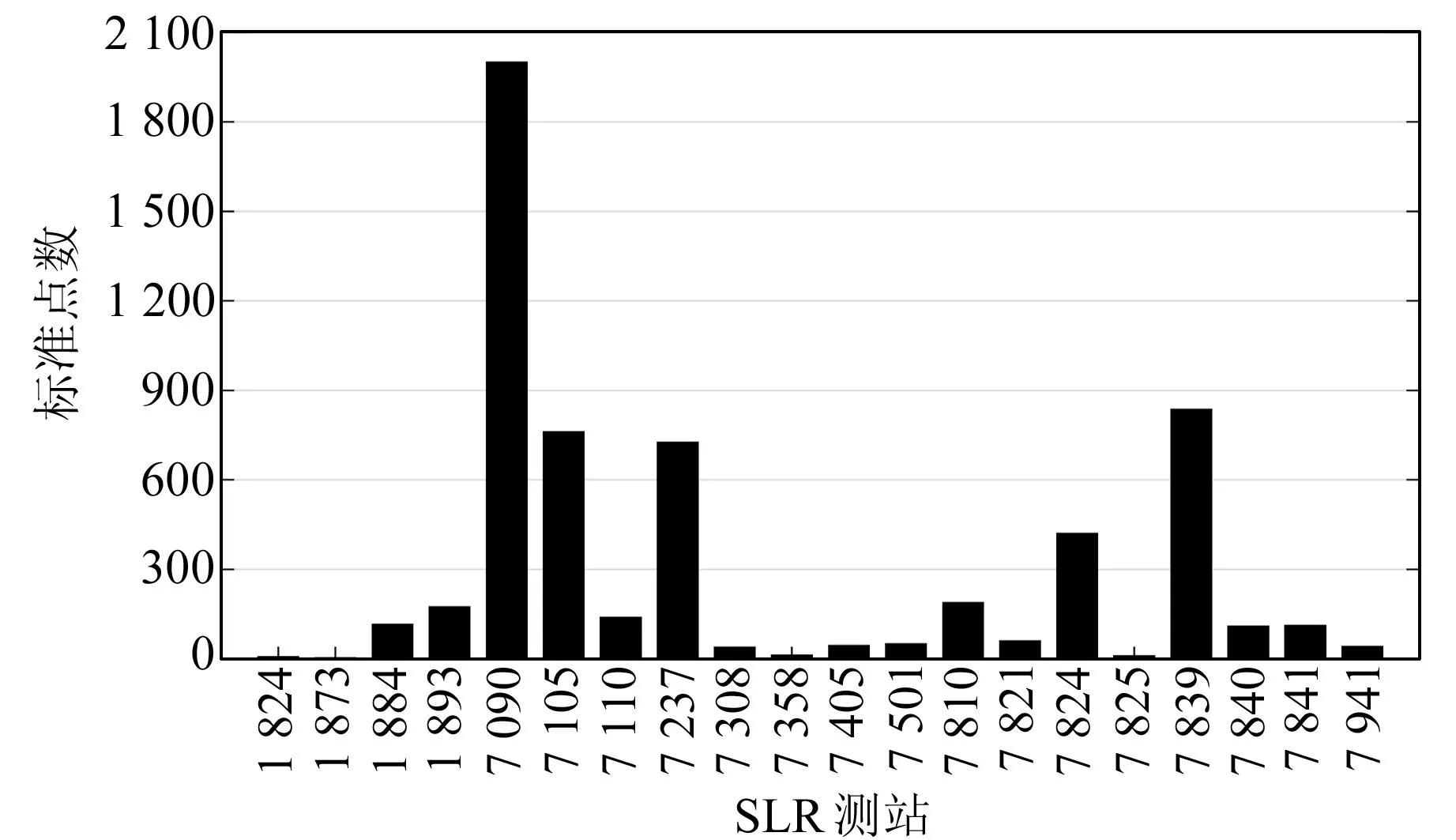
图1　2009-10-01～2010-01-31期间GOCE卫星SLR观测数据统计Fig.1　SLR observations of GOCE satellite from 2009-10-01 to 2010-01-31

选取具有代表性的两个测站——位于北半球的GRAZ站(7839)和位于南半球的Yarragadee站(7090)，各选择一段降弧和升弧，分析单个观测弧段的残差特征。基于上述数据预处理模型，取15°截止高度角，测站时距偏差消除前和消除后残差特性如图2所示。设置15°截止高度角是因为低高度角的观测有较大的对流层延迟，带来较大误差。可以看到：1)在大于15°高度角范围内，SLR观测存在明显的系统性误差，呈线性变化趋势。这与上述时距偏差模型(式(4))中残差在一个弧段内线性变化的理论吻合，因此可采用该时距偏差模型拟合残差，消除测站时距偏差的影响。

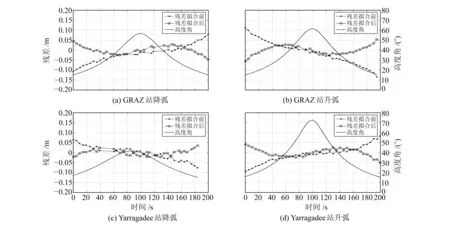
图2　单弧段残差序列Fig.2　Single pass residuals time series

2)利用式(4)拟合残差后，残差量级有明显减小，基本小于5 cm，线性项趋势消失，但还存在某些较小的系统性误差，这可能是由于采用的对流层延迟模型未考虑对流层水平梯度所致[4,10]。3)同测站的升弧和降弧的残差线性变化趋势相反(图2(a)和图2(b)，图2(c)和图2(d))，不同半球同降弧或同升弧的残差线性变化趋势相反(图2(a)和图2(c)，图2(b)和图2(d))，这样解出的时间偏差参数对于同一测站的升弧和降弧符号也相反。

采用上述数据处理模型，每站每弧段估计一组时距偏差参数。消除测站时距偏差影响后，轨道检核结果的残差序列如图3所示。图中残差均小于1 dm，且绝大部分小于5 cm，集中在理论值0上下分布。

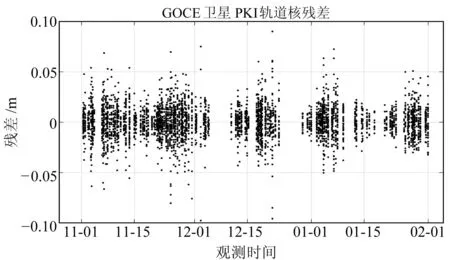
图3　轨道检核残差序列Fig.3　Time series of orbit validation residuals

轨道精度检核的统计结果如表2所示。截止高度角15°，剔除残差值较大的标准点和观测数过少的弧段后，总标准点数减少1/4。这主要是因为GOCE卫星轨道过低，较难跟踪。表2检核结果显示，GOCE卫星的PKI轨道无系统性偏差，外符合精度为1.53 cm。与Bock等[2]的检核结果(平均值0.88 cm，RMS为2.23 cm)相比，本文的结果进一步削弱了系统偏差，RMS提高约0.7 cm。这主要是因为本文相对文献[2]设置了15°截止高度角，采用了测站时距偏差模型消除测站系统偏差。

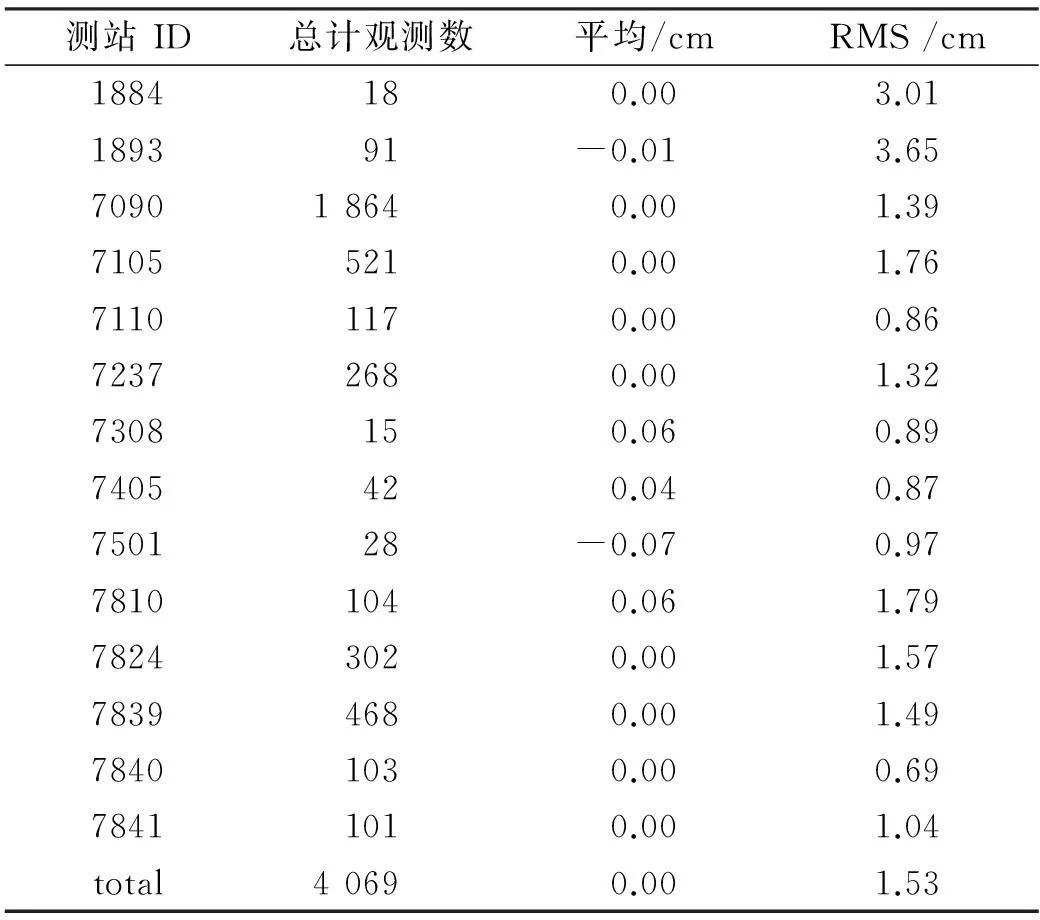
表2　GOCE卫星轨道检核统计结果

为进一步分析截止高度角和时距偏差模型对检核结果的影响，设计4种实验方案分别计算各方案中SLR检核结果，如表3所示。结果显示，设置一定的截止高度角，检核精度有小幅度提高；采用时距偏差模型能有效消除系统偏差，且检核精度有较大提高。表3定量分析了图2中采用时距偏差模型的影响，也揭示了本文相对于Bock等[2]的检核结果在系统偏差和精度上提高的主要原因。

表3　截止高度角和时距偏差模型的影响

时距偏差是测站系统性能的一个重要指标。图4展示了Yarragadee(7090)站时间偏差和距离偏差参数的解算结果，该结果剔除了时间偏差>40 μs的弧段。可以看到，时间偏差除个别外均稳定在±10 μs内，距离偏差稳定在±5 cm内，其绝对值的均值分别为7.60 μs和1.11 cm，该结果与文献[11]中的时距偏差结果类似。总体来说，测站时距偏差参数变化比较均匀，起伏不大，说明该测站系统性能较稳定。

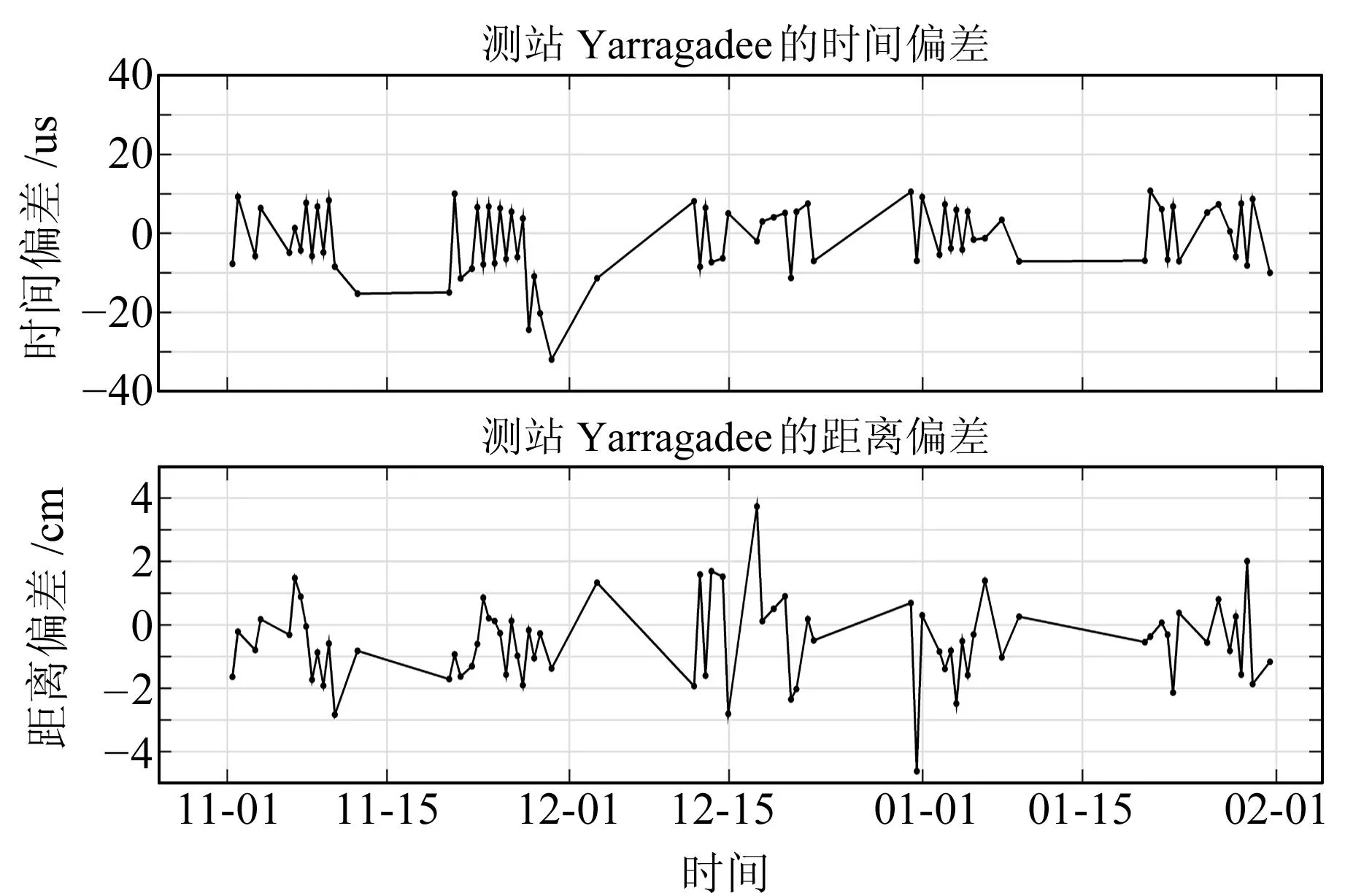
图4　Yarragadee站时距偏差变化Fig.4　Variation of station Yarragadee’s time bias and range bias

3　结　语

1)本文利用SLR对GOCE卫星的PKI精密轨道作外部检核，数据处理过程中发现，检核残差存在系统误差，原因是SLR测距系统存在测站时距偏差。引入时距偏差模型拟合后，残差的系统误差明显减弱。

2)检核结果表明，GOCE卫星PKI轨道外符合精度为1.53 cm，无系统性偏差。与Bock等[2]的检核结果相比，进一步削弱了系统性偏差，且精度提高约0.7 cm，主要原因是本文引入了时距偏差模型并消除了测站时距偏差。

3)估算的测站时距偏差参数可作为测站系统质量和性能的参考指标。图4显示，Yarragadee测站系统性能整体稳定。

致谢：感谢ILRS数据中心提供SLR观测数据！

参考文献

[1]Gruber T, Rummel R, Abrikosov O. GOCE L2 Product Data Handbook[Z]. EGG-C, 2009

[2]Bock H, Jäggi A. GPS-derived Orbits for the GOCE Satellite[J]. Journal of Geodesy, 2011, 85(11): 807-818

[3]Xu G C. Science of Geodesy-I: Advances and Future Directions[M]. Berlin: Springer, 2010

[4]Petit G, Luzum B. IERS Conventions(2010)[R]. Bureau International des Poids et Mesures Sevres, France, 2010

[5]Montenbruck O, Neubert R. Range Correction for the CryoSat and GOCE Laser Retroreflector Arrays[Z].DLR/GSOC, 2011

[6]Bigazzi A, Frommknecht B. Note on GOCE Instruments Positioning-Memo_3.1_[XGCE-GSEG-EOPG-TN-09-0007 v3.1][Z]. ESA, 2010

[7]冯初刚, 朱元兰. 1992年LAGEOS卫星全球SLR标准点资料的分析[J]. 中国科学院上海天文台年刊, 1995, 16: 107-112(Feng Chugang, Zhu Yuanlan. Analysis for LAGEOS SLR Global Normal Point Data of 1992[J]. Annals of Shanghai Observatory Academia Sinica, 1995, 16: 107-112)

[8]冯初刚, 朱元兰, 张飞鹏. LAGEOS卫星精密定轨及残差分析[J]. 天文学报, 2003, 44(1): 55-64(Feng Chugang, Zhu Yuanlan, Zhang Feipeng. Determination of LAGEOS Satellite’s Precise Orbits and Residual Analysis[J]. Acta Astronomica Sinica, 2003, 44(1): 55-64)

[9]祝芙英, 吴云, 杜瑞林, 等. 流动SLR乌鲁木齐站观测精度评估[J]. 大地测量与地球动力学, 2008, 28(2): 127-131(Zhu Fuying, Wu Yun, Du Ruilin, et al. Accuracy of Mobile SLR at Urumchi Station[J]. Journal of Geodesy and Geodynamics, 2008, 28(2): 127-131)

[10]Hulley G C, Pavlis E C. A Ray-tracing Technique for Improving Satellite Laser Ranging Atmospheric Delay Corrections, Including the Effects of Horizontal Refractivity Gradients[J].Journal of Geophysical Research: Solid Earth, 2007, 112(B6)

[11]赵春梅, 瞿锋, 程鹏飞, 等. 阿根廷圣胡安激光测距系统的SLR数据质量分析[J]. 测绘学报, 2008, 37(3): 338-341(Zhao Chunmei, Qu Feng, Cheng Pengfei, et al. Data Quality Analysis of Argentina San Juan Laser Ranging System[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 338-341)

Foundation support:National Key Basic Research Program of China, No. 2013CB733301; National Natural Science Foundation of China, No. 41004007, 41274033; Special Fund for Public Welfare Industry (Surveying,Mapping and Geoinformation), No. 201512001; Fundamental Research Funds for the Central Universities, No. 2015214020202.

About the first author:ZHONG Luping, postgraduate, majors in satellite laser ranging, E-mail: lpzhong@whu.edu.cn.

收稿日期：2015-08-14

第一作者简介：衷路萍，硕士生，主要研究方向为人卫激光测距，E-mail：lpzhong@whu.edu.cn。 通讯作者：邹贤才，博士，副教授，主要研究方向为卫星大地测量和物理大地测量，E-mail：xczou@whu.edu.cn。

DOI：10.14075/j.jgg.2016.08.014

文章编号：1671-5942(2016)08-0719-04

中图分类号：P228

文献标识码：A

Corresponding author:ZOU Xiancai, PhD, associate professor, majors in satellite geodesy and physical geodesy, Email: xczou@whu.edu.cn.

Evaluation of GOCE Precise Orbit Using SLR

ZHONGLuping1ZOUXiancai1WULinchong1YUNan1

1School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China

Abstract:In this paper we present the method of satellite orbit validation with SLR measurements, and use SLR data observed from 1 November 2009 until 31 January 2010 (3 months) to validate the GOCE PKI (precise kinematic) orbit. Based on residual analysis, we find that system error due to station time bias and range bias exits and has not been removed in the SLR observation. After modeling and fitting the station time bias and range bias, we achieve the GOCE PKI orbit precision at the level of 1.5 cm.

Key words:precise orbit; SLR; validation; station time bias and range bias

项目来源：国家973计划(2013CB733301)；国家自然科学基金(41004007, 41274033)；测绘地理信息公益性行业科研专项(201512001)；中央高校基本科研业务费(2015214020202)。