基于Levenberg-Marquarat算法的非线性三维直角坐标转换方法

闻洪峰　和　会

1　武汉大学测绘学院，武汉市珞喻路129号，430079　2　河北省第一测绘院，石家庄市中山东路495号，050032　3　河北省基础地理信息中心，石家庄市中山东路495号，050032



基于Levenberg-Marquarat算法的非线性三维直角坐标转换方法

闻洪峰1,2和会3

1武汉大学测绘学院，武汉市珞喻路129号，4300792河北省第一测绘院，石家庄市中山东路495号，0500323河北省基础地理信息中心，石家庄市中山东路495号，050032

摘要：提出一种基于Levenberg-Marquarat算法的非线性三维直角坐标转换方法,在法矩阵病态或者奇异时依然有效，并通过修正旋转角参数的方法，有效解决了平移量与旋转角量纲不同造成的迭代发散问题。设计出简洁有效的迭代求解模式,获得了稳定的参数解。最后通过模拟数据对比分析,证明该方法的有效性和正确性。

关键词：Levenberg-Marquarat算法;坐标转换;七参数;病态;奇异

传统的三维直角坐标转换通常采用线性化的七参数模型，该模型只适用于小旋转角，不适合于大旋转角的三维直角坐标转换问题[1-4]。许多学者对大旋转角的三维直角坐标转换问题进行研究。文献[1]分析局部区域三维七参数转换中平移参数与旋转参数的强相关性，提出通过正则化方法改善参数解的精度；文献[2]提出基于改进的高斯-牛顿法的非线性三维直角坐标转换方法；文献[3]在文献[2]的基础上通过对坐标进行中心化，省却了计算搜索步长的过程；文献[4]通过变更求解参数的方式解决了7参数量纲差异的问题，提高了收敛性和解的稳定性。文献[1]提出七参数转换中法方程病态的一种处理思路，但却是针对传统的七参数线性模型的。文献[2-4]都是针对七参数非线性模型的，但都要求法矩阵为良态，在法矩阵呈病态或奇异时计算结果将很不稳定。本文提出一种基于Levenberg-Marquarat算法的非线性三维直角坐标转换方法。该方法不仅适合小旋转角，也适用于大旋转角的三维坐标转换，在法矩阵病态或奇异时仍能正确解算，并通过旋转角修正保证解的收敛性及稳定性。

1　Levenberg-Marquarat算法

Levenberg-Marquardt算法[5]既具有最速下降法的收敛速度，又克服了Gauss-Newton法对初始值的苛刻要求，同时在法方程病态或奇异时也仍然有效。

设性能优化指数F(x)的牛顿方法是：

(1)

式中，A(X(k))=2F(X(k)),g(X(k))=F(X(k))，上标表示迭代次数，X为输入量(待求参数)向量矩阵，x为向量矩阵的元素。

如果设F(x)是残差平方函数之和，即

(2)

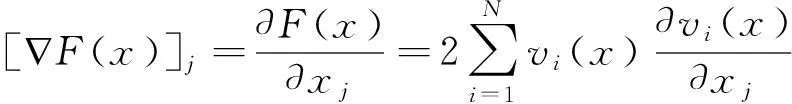
(3)

其中，

N为输出量个数，n为输入量个数。

赫森矩阵可表示为：

(4)

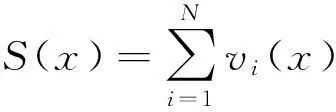
(5)

将式(3)和式(5)代入式(1)，可以得到高斯-牛顿算法的迭代算式：

(6)

问题是，H=JT(X(k))J(X(k))可能不可逆，这时可以采用改进的近似赫森矩阵：

(7)

设H的特征值和特征向量分别为{λ1,λ2,…,λn}和{z1,z2,…,zn}，则有：

(8)

因此，G与H的特征向量相同，且G的特征值为λi+μ,对所有的λi，增加μ以保证λi+μ>0，则G必定正定可逆。从而得到LM算法的迭代算式：

(9)

2　数学模型

三维直角坐标转换模型[2]可表示为：

(10)

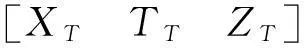
式中，

式(10)可表示为如下形式：

(11)

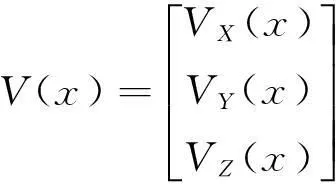
根据Levenberg-Marquardt算法，针对每个坐标转换用的公共点，可列出如下迭代公式：

(12)

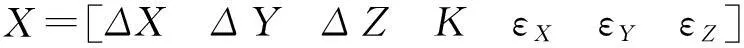
从参数初值X0出发，按照上式估计出近似值X(k),然后以该近似值作为下一次迭代的初值计算X(k+1)。反复迭代，逐次逼近真正的极小点。

通常，μ的初值μ0可取(0,1)之间的任意小数，然后根据V(k)和V(k+1)来调整μ(k+1)，即

(13)

一般情况下,μ会随着改正量的减小而逐步减小，有时会减小至非常趋近于0的小数，这时如果式(12)中方程系数阵JT(X(k))J(X(k))病态或奇异，则μ不能起到很好的修正作用。因此，在迭代过程中，如果μ小于某一阉值τ0(人为设定μ的最小值，本文取0.000 000 01)，应该将其固定在阈值处，这样既能保证系数矩阵可逆，同时由于μ值非常小，在系数矩阵非奇异的情况下也几乎不会对最优解产生影响。

另外，由于三角函数具有周期性，而平移参数的平移量又可能非常大，在局部区域，二者具有较强的相关性。在迭代过程中,3个旋转角有可能会跟随平移量逐渐增大，这时如果不加以处理，旋转参数有时会由于改正过于剧烈而无法正确收敛。因此，笔者在迭代过程中不断对旋转参数进行修正，即每次迭代改正后，将旋转参数加减360°的整数倍，将其调整至0°～360°之间。

基于Levenberg-Marquarat算法的非线性三维直角坐标转换方法步骤如下：

2)根据式(12)列出误差方程，若有n个基准点,可组成3n个误差方程，并计算参数X(k+1)；

3)根据式(11)计算VTV(k)和VTV(k+1)，如果VTV(k)和VTV(k+1)的差值绝对值小于给定的阈值ξ0(表征期望的收敛精度，本文取ξ0=0.000 000 001),则转至步骤8)；

4)对X(k+1)中旋转参数进行修正，如果εX<0，则εX=εX+(int(εX/360)+1)×360；如果εX≥0，则εX=εX-int(εX/360)×360，εY、εZ作相同处理；

5)根据式(13)计算μ(k+1)；

6) 判断μ(k+1)是否小于给定阈值τ0(本文取τ0=0.000 000 01)，若小于阈值τ0，则取μ(k+1)=τ0;

7)转至步骤2)；

8) 输出最终的转换参数Xk+1,迭代结束。

3　算例和分析

算例1模拟算例来自文献[2]和文献[3]，变换前后的坐标如表1。

根据本文推导的基于Levenberg-Marquarat算法的七参数严密解算公式和计算步骤,在VisualC++6.0中编程,计算结果如下:旋转角εX=29°59′59.999 941″,εY=44°59′59.999 996″,εZ=60°00′00.000 068″;尺度比例 K=1.000 000 000 1;平移参数ΔX=500.000 0m,ΔY=1 000.000 0m,ΔZ=2 000.000 0m。结果与实际采用的变换参数相一致[2-3]，表明本文的方法是有效可靠的。

算例2模拟算例来自文献[4]，变换前后的坐标如表2。

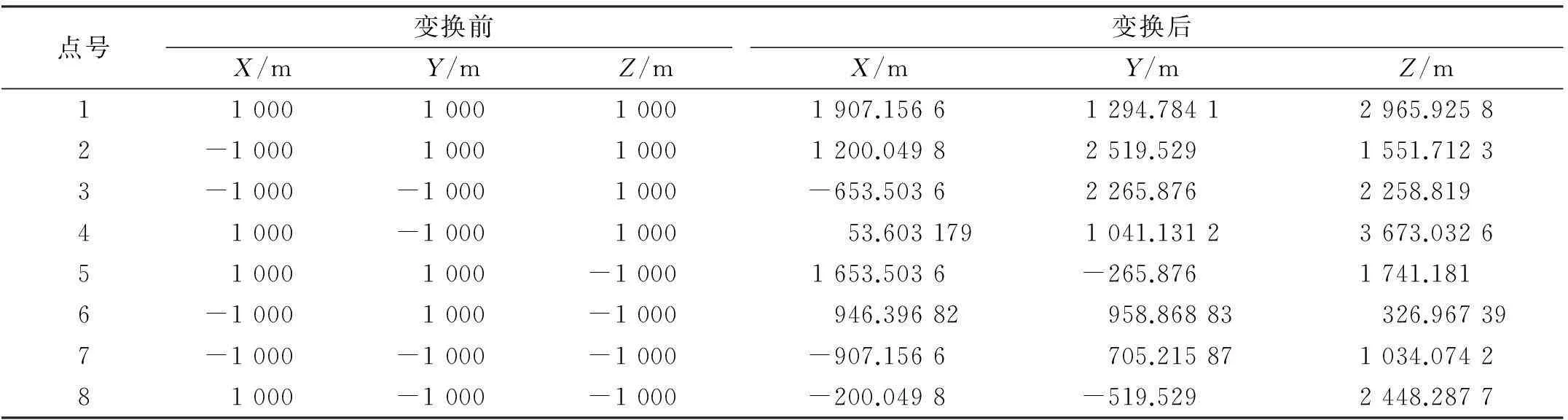
表1　算例1示例数据

表2　算例2示例数据

根据本文推导的基于Levenberg-Marquarat算法的七参数严密解算公式和计算步骤,取2、3、4、5号点为已知点，1号点为检查点，转换参数计算结果如下:旋转角εX=142°04′11.790 503″,εY=229°03′03.348 73″,εZ=12°54′30.581 561″;尺度比例K=0.999 923 072 0;平移参数ΔX=-2 831 698.766 1 m,ΔY=4 675 677.770 0 m,ΔZ=3 275 369.428 0 m。已知点转换残差及检核点残差如表3所示。

由表3的残差统计可见，转换精度在mm级，与文献[4]的转换精度相当。而对于算例2，如果采用高斯-牛顿方法，则迭代发散、无法收敛。

表3　算例2残差统计

4　结　语

本文提出的基于Levenberg-Marquarat算法的非线性三维直角坐标转换方法,不需要中心化、正则化、计算搜索步长及变更求解参数，相比文献[2-4]的算法更加简单、易行。由于Levenberg-Marquarat算法的特性，本文方法属于全局收敛，即便系数矩阵病态或奇异，仍能稳定收敛并得到可靠结果。由于旋转角与平移量量纲不同，二者在数值上相差很大时可能会造成不收敛现象，通过迭代过程中对旋转角的不断修正，可以有效保证收敛性及解的稳定性。

参考文献

[1]沈云中,胡雷鸣,李博峰. Bursa模型用于局部区域坐标变换的病态问题及其解法[J].测绘学报, 2006, 35 (2):95-98(Shen Yunzhong, Hu Leiming,Li Bofeng. Ill-Posed Problem in Determination of Coordinate Transformation Parameters with Small Area’s Data Based on Bursa Model [J].Acta Geodaetica et Cartographica Sinica,2006,35(2):95-98)

[2]罗长林,张正禄,邓勇，等.基于改进的高斯-牛顿法的非线性三维直角坐标转换方法研究[J].大地测量与地球动力学,2007,27(1): 50-53(Luo Changlin,Zhang Zhenglu,Deng Yong,et al.On Nonlinear 3D Rectangular Coordinate Transformation Method Based on Improved Guss-Newton Method [J]. Journal of Geodesy and Geodynamics,2007,27(1):50-53)

[3]刘仁钊,段文贵，张玉堂.Bursa转换模型七参数严密解算方法研究[J].资源环境与工程，2010,24(4)：416-423(Liu Renzhao,Duan Wengui,Zhang Yutang. Study on Close Computation of Parameters of Bursa Transformation Model[J].Resources Environment & Engineering, 2010,24(4)：416-423)

[4]李金岭,刘鹂,乔书波,等. 关于三维直角坐标七参数转换模型求解的讨论[J].测绘科学，2010,35(4)：76-78(Li Jinling,Liu Li,Qiao Shubo,et al. Discussion on the Determination of Transformation Parameters of 3D Cartesian Coordinates[J]. Science of Surveying and Mapping,2010,35(4)：76-78)

[5]王解先.七参数转换中参数之间的相关性[J].大地测量与地球动力学,2007,27(2):43-46(Wang Jiexian. Correlations Among Parameters in Seven-Parameter Transformation Model [J].Journal of Geodesy and Geodynamics, 2007,27(2):43-46)

[6]姚吉利.三维坐标转换参数直接计算的严密公式[J].测绘通报, 2006(5):7-10(Yao Jili.Rigorous Formula for Direct Calculating Parameter in 3D Transformation[J].Bulletin of Surveying and Mapping, 2006(5):7-10)

[7]Awange L J, Grafarend E W. Closed Form Solution of the Over Determined Nonlinear 7 Parameter Datum Transformation [J]. AVN, 2003(4): 130-148

[8]李潇,尹晖.基于最小二乘配置的三维空间坐标转换[J]. 测绘工程, 2008,17(2):16-18(Li Xiao,Yin Hui. Three-Dimensional Spatial Coordinate Transformation Based on Least Squares Collocation[J].Engineering of Surveying and Mapping, 2008,17(2):16-18)

[9]陈宇,白征东,罗腾.基于改进的布尔沙模型的坐标转换方法[J]. 大地测量与地球动力学,2010,30(3):71-73(Chen Yu,Bai Zhengdong,Luo Teng.An Improved Bursa Model for Coordinate Transformation[J]. Journal of Geodesy and Geodynamics, 2010,30(3):71-73)

[10]沈云中,卫刚.利用过渡坐标系改进3维坐标变换模型[J]. 测 绘 学 报,1998,27(2):161-165(Shen Yunzhong,Wei Gang.Improvement of Three Dimensional Coordinate Transformation Model by Use of Interim Coordinate System[J].Acta Geodaetica et Cartographica Sinica,1998,27(2):161-165)

[11]陈义, 沈云中, 刘大杰. 适用于大旋转角的三维基准转换的一种简便模型[J].武汉大学学报:信息科学版,2004,29(12):1 102-1 104(Chen Yi,Shen Yunzhong,Liu Dajie.A Simplified Model of Three Dimensional-Datum Transformation Adapted to Big Rotation Angle[J].Geomatics and Information Science of Wuhan University, 2004,29(12):1 102-1 104)

[12]胡亚江,杨晓梅,沙月进.大欧拉角的空间直角坐标转换方法探讨[J].现代测绘,2006,29(6):10-12(Hu Yajiang,Yang Xiaomei,Sha Yuejin. Discussion on the Way of Space Right-Angle Coordinate Transform of the Big Euler Angle[J].Modern Surveying and Mapping, 2006,29(6):10-12)

[13]Grafarend E W, Awange L J. Nonlinear Analysis of the Three-dimensional Datum Transformation[J]. Journal of Geodesy, 2003,77:66-76

[14]王建梅,覃文忠. 基于LM算法的BP神经网络分类器[J]. 武汉大学学报:信息科学版, 2005, 30(10):928-931(Wang Jianmei,Qin Wenzhong.BP Neural Network Classifier Based on Levenberg-Marquardt Algorithm[J]. Geomatics and Information Science of Wuhan University, 2005, 30(10):928-931)

[15]赵双明,郭秋燕,罗研,等. 基于四元数的三维空间相似变换解算[J].武汉大学学报：信息科学版, 2009,34(10):1 214-1 217(Zhao Shuangming,Guo Qiuyan,Luo Yan,et al.Quaternion-Based 3D Similarity Transformation Algorithm[J]. Geomatics and Information Science of Wuhan University, 2009,34(10):1 214-1 217)

About the first author:WEN Hongfeng, engineer, majors in GPS data process and regional surface subsidence monitoring by InSAR,E-mail：81350890@qq.com.

收稿日期：2015-08-30

第一作者简介：闻洪峰，工程师，主要研究方向为GPS数据处理及InSAR区域变形监测,E-mail：81350890@qq.com。

DOI：10.14075/j.jgg.2016.08.018

文章编号：1671-5942(2016)08-0737-04

中图分类号：P226

文献标识码：A

A Nonlinear 3D Rectangular Coordinate Transformation Method Based on Levenberg-Marquarat Algorithm

WENHongfeng1,2HEHui3

1School of Geodesy and Geomatics,Wuhan University，129 Luoyu Road,Wuhan 430079,China2The First Surveying and Mapping Institute of Hebei Province，495 East-Zhongshan Road,Shijiazhuang 050032，China3Basic Geographic Information Center of Hebei Province，495 East-Zhongshan Road, Shijiazhuang 050032，China

Abstract:A nonlinear 3D rectangular coordinate transformation method based on the Levenberg-Marquarat algorithm,which is effective when normal equation is ill-conditioned or singular,is proposed. The problem of divergencein the process of iteration,which arises due to different dimensions between translation amount and rotation angle,is effectively resolved.A neat and effective model of iterative solving is designed and a stable parametric solution is achieved.Finally, the effectiveness and correctness of the method is proven by comparative analysis of simulated data.

Key words:Levenberg-Marquarat algorithm；coordinate transformation;seven-parameter; ill-conditional; singular