华北地区GPS基准站坐标时间序列噪声特征研究
吴伟伟 孟国杰 伍吉仓
1 同济大学测绘与地理信息学院,上海市四平路1239号,200092 2 中国地震局地震预测研究所,北京市海淀区复兴路63号,100086
华北地区GPS基准站坐标时间序列噪声特征研究
吴伟伟1,2孟国杰2伍吉仓1
1同济大学测绘与地理信息学院,上海市四平路1239号,2000922中国地震局地震预测研究所,北京市海淀区复兴路63号,100086
摘要:利用华北地区GPS连续运行基准站网络2008-08~2013-04观测数据,分析36个基准站坐标时间序列的噪声特征。利用区域堆栈滤波方法对GPS单日解坐标时间序列进行共性误差剔除,使用极大似然估计准则定量估计坐标时间序列的噪声特性,并分析有色噪声对测站计算速度的影响。结果表明,华北地区GPS基准站坐标时间序列的共性误差在N、E和U方向分别约为1 mm、1 mm和3 mm,且共性误差具有类似闪烁噪声的特性;共性误差剔除前,坐标时间序列的噪声特性可以用可变白噪声加闪烁噪声模型或可变白噪声加幂律噪声模型来描述;共性误差剔除后降低了坐标时间序列噪声中闪烁噪声的成分,突出了本地效应部分噪声,坐标时间序列的噪声特性可以用可变白噪声加闪烁噪声和随机漫步噪声模型或可变白噪声加幂律噪声模型来描述;最优噪声模型计算的速度误差比仅考虑可变白噪声所计算的速度误差增大5~8倍;剔除共性误差,可使测站速度的精度获得40%左右的提高。
关键词:坐标时间序列;区域堆栈滤波法;极大似然估计;噪声模型;速度误差
分析GPS连续基准站观测数据获取的坐标时间序列的噪声特征,是获取GPS测站速度的重要组成部分[1-4]。不仅有助于获取准确的GPS测站速度,而且可以进一步揭示噪声的地球物理本源,对GPS测站建设以及数据处理策略等均有一定的指导意义[5-7]。本文详细分析了华北地区GPS连续基准站坐标时间序列的噪声特征,旨在获得该地区准确的区域地壳形变信息。
1 GPS观测资料与数据处理
选择36个华北地区GPS连续基准站2008-08~2013-04观测数据,其中5个陆态网络Ⅰ期站点数据时间跨度约4.5 a,24个陆态网络Ⅱ期站点数据时间跨度约2.5 a。另外,在中美国际合作项目(ICP)支持下,项目组还建立了7个GPS连续站,用于监测张渤带、郯庐带的活动特征,这些测站数据的时间跨度为2~4.5 a。图1为华北区域GPS站点的分布与类别,灰色线段为第四纪活动断层。
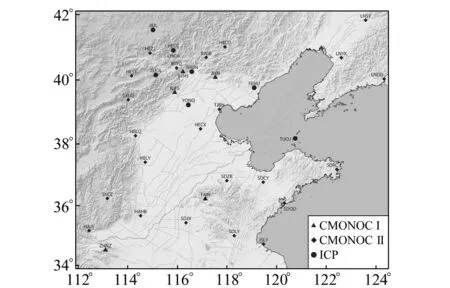
图1 华北地区GPS基准站分布Fig.1 Distribution of GPS fiducial stations in north China
采用Bern 5.0软件[8]处理GPS连续基准站观测数据,主要包括单点定位、基线处理和联网解算3个步骤:1)利用PPP单点定位BPE处理工具对测站GPS观测数据RINEX文件逐一进行单日解解算,获取测站的单日初始坐标;2)选用“共同观测数量最大”准则组成GPS相位双差基线,对流层模型选用GMF映射函数每2 h估计一次拟合参数,相位模糊度选用“伪自由电离层组合”策略对独立基线进行逐条解算,从而逐条获取独立基线解(为保证时间序列跨度内所有数据处理保持框架统一,选择中国及周边不受2011年日本东北地震影响的10个IGS站(SHAO、TWTF、WUHN、URUM、GUAO、KUNM、LHAZ、IRKJ、YSSK、BJFS)与华北地区测站组成GPS观测网进行基线解算);3)利用序贯平差工具,顾及基线之间的相关性,联合相位模糊度固定后的GPS双差相位观测值进行整体解算,选用ITRF2008框架下10个框架站坐标重心作为解算基准获取测站单日约束解,组成测站在ITRF2008框架下的三分量(N、E、U)坐标时间序列。
图2给出CMONOC Ⅰ、ICP及CMONOC Ⅱ三类GPS连续基准站的数据时段信息。共有9个测站的坐标序列长度大于3 a,余下测站的坐标序列长度平均为2~3 a;半数以上测站的坐标序列存在大于总长度10%的间隔,最大间隔率达到35.3%。

图2 华北地区GPS基准站时间序列数据分布Fig.2 Data availability for GPS fiducial stations in north China
2 测站坐标时间序列分析
2.1共性误差分析
华北地区GPS网测站观测时段存在很大差异,观测时长也存在很大的不连续性,不满足主成分分析[7]滤波对数据连续性的要求。因此,本文采用堆栈滤波法[9]进行共性误差分析。
利用最小二乘拟合坐标时间序列获取GPS坐标残差时间序列,常用的拟合函数模型包含线性项、周期项(年周期项及半年周期项)、跳变项以及残差项[6]。设有n个基准站,进行了m个历元观测,坐标残差时间序列(N、E、U三分量)可表示为Vi,k(i=1,2,3,…,m; k=1,2,3…n)。对区域网内所有站点残差进行加权平均,并作为整个区域GPS网的共性误差:
(1)
式中,Vi,k表示第i历元第k测站对应的坐标残差值,σi,k为相应的坐标单日解中误差。从原始GPS坐标时间序列中扣除共性误差成分,即获得剔除共性误差后的GPS坐标时间序列。
2.2噪声分析
对GPS坐标残差时间序列进行频谱分析发现,其功率谱曲线的低频部分具有明显的有色噪声特性,而高频部分主要是平稳白噪声成分[10-15]。对坐标时间序列进行最小二乘拟合时,模型参数解及参数协方差计算由模型拟合的函数模型A阵和随机模型C阵共同决定[13],其中随机模型C阵由坐标时间序列残差(噪声)特性确定。因此,拟合GPS坐标时间序列时需要考虑其准确的噪声特性:
(2)
式中,y表示原始坐标时间序列,x表示拟合模型参数解,Cx表示拟合参数协方差阵,A 表示拟合系数阵,C表示拟合协方差阵。
利用极大似然估计(MLE)方法确定坐标时间序列的噪声特性[12-15]。假定GPS坐标残差时间序列由有色噪声和白噪声的某种组合形式组成,计算联合概率密度的自然对数函数,确定各噪声分量的大小,使得极大似然函数值(MLE)最大:
C=a2I+b2J, ln[lik(v,C)]=
(3)
式中,N表示时间序列长度,C表示噪声组合组成的协方差阵,v表示协方差阵为C时的加权最小二乘残差,I 表示白噪声组成的协方差阵,J 表示有色噪声组成的单位协方差阵。

图3 噪声模型的定义Fig.3 Definition of noise model
分析两种白噪声模型与6 种有色噪声模型所组成的噪声模型组合。白噪声模型包括简单白噪声模型(WH)和可变白噪声模型(VW);有色噪声模型包括幂律噪声模型(PL)、闪烁噪声模型(FN)、随机漫步噪声模型(RW)、闪烁噪声与随机漫步噪声组合模型(FN+RW)、一阶高斯马尔科夫噪声模型(GM)、一般高斯马尔科夫噪声模型(GG)。各种噪声模型的单位协方差矩阵或功率谱见图3。图中,C 表示噪声协方差阵,Pf表示噪声功率谱,P0表示功率谱常量,f 表示频率,κ 表示功率谱系数,β/2π表示功率谱交叉频率。
将白噪声与有色噪声模型组合成14对噪声模型组合:WH、FN+WH、RW+WH、FN+RW+WH、PL+WH、GM+WH、GG+WH和VW、FN+VW、RW+VW、FN+RW+VW、PL+VW、GM+VW、GG+VW,结合最小二乘拟合函数模型以及式(2)、(3)对坐标时间序列进行噪声特性分析。
3 结果与分析
3.1共性误差
共性误差坐标时间序列水平分量幅值约为1 mm,垂直分量幅值约为3 mm。采用Lome Scargle周期图方法[2,11,13]计算共性误差功率谱图,共性误差具有明显的有色噪声特性。对共性误差坐标时间序列的功率谱进行线性拟合,N、E、U的拟合功率谱系数分别为-0.85、-0.91、-0.84,均接近于-1。因此,共性误差坐标时间序列具有明显的有色噪声特性,且近似于闪烁噪声:
(4)
3.2噪声特性
利用极大似然估计准则定量测试14种噪声组合模型。根据不同的极大似然估计函数拟合自由度,Langbein给出了以极大似然函数值为判断依据的经验标准[15]:当两种模型的拟合自由度相同时,MLE更大(MLE差值δMLE>0)的噪声模型更优;当两种模型的拟合自由度相差1时,δMLE=2.6作为模型显著区分的阈值;当两种模型的拟合自由度相差2时,δMLE=5.2作为模型显著区分的阈值。
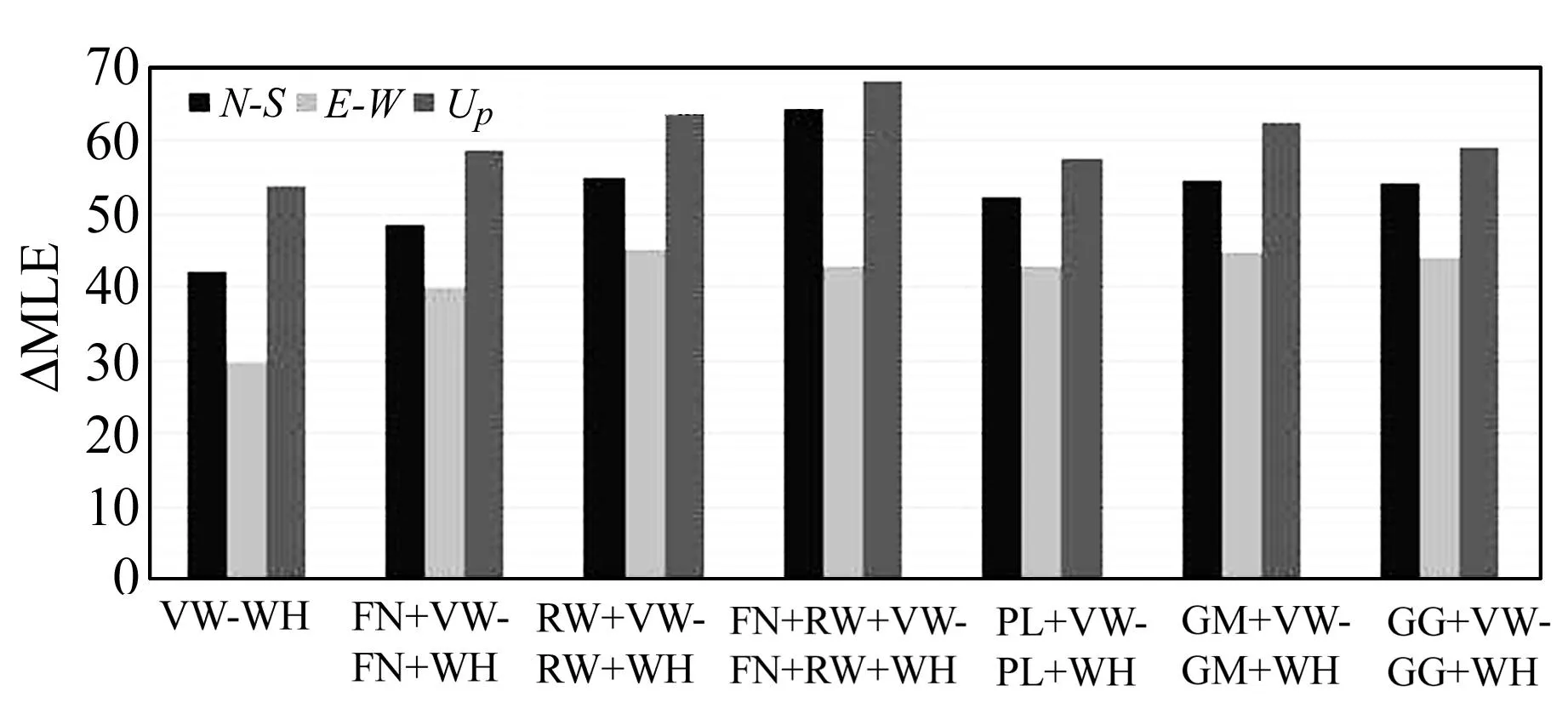
图4 VW组合模型与相应WH组合模型的平均δMLE差Fig.4 Average δMLE between VW group and WH group
3.2.1白噪声模型选择
如图4所示,对比WH组合与相应VW组合的MLE,绝大部分站点的VW组合优于WH组合;VW组合的平均δMLE远大于0。另外,WH组合模型假设下,极大似然估计经常出现无法估计白噪声幅值的情形,而VW组合模型中类似情形极少。因此,VW更接近于GPS坐标时间序列真实噪声中的白噪声特性,考虑单日解处理的中误差对确定拟合随机模型十分必要。
3.2.2有色噪声模型选择
1)VW与VW和有色噪声组合对比。
如图5所示,共性误差剔除前后的所有VW与有色噪声组合的MLE均值,均显著大于单纯VW下的MLE,表明VW与有色噪声组合模型优于VW模型。

图5 VW和有色噪声组合模型与VW模型的平均δMLE差Fig.5 Average δMLE between VW and combinations of VW and color noise
2)VW和有色噪声组合之间的对比。
如图5所示,共性误差剔除前,RW+VW组合的MLE最小,FN+RW+VW组合下大部分(88%)站点的RW分量无法成功估计,表明坐标时间序列中未发现明显的具有代表站点效应的RW分量[13],这可能是由于坐标时间序列长度过短导致RW成分被FN成分掩盖。PL+VW组合与FN+VW组合的MLE值相近,δMLE小于阈值2.6,且PL的三分量功率谱系数分别为-1.04±0.13、-1.07±0.10、-1.03±0.15,与FN的谱系数-1相近。GM+VW组合和GG+VW组合的均值δMLE均小于阈值5.2,对于部分大于阈值的站点,其功率谱交叉频率远大于1 cpy,较大的交叉频率表示时间序列表现为低频不相关特性[15],这一现象与实际噪声的功率谱(低频相关性大,高频不相关)不一致,表明FN+VW组合或PL+VW组合是共性误差剔除前坐标时间序列噪声特性的最优表示模型。
共性误差剔除后,FN+VW组合的MLE最小,FN+RW+VW组合中RW成分成功估计的比率(59%)明显提高,PL+VW组合的三分量功率谱系数分别降低为-1.38±0.36、-1.37±0.38、-1.28±0.32,说明剔除共性误差降低了噪声中的具有全局分布特性的FN成分,使具有站点效应的RW成分部分表现出来。对比FN+RW+VW、PL+VW、GM+VW、GG+VW与RW+VW之间的δMLE,均值均大于相应阈值,其中排除由于交叉频率过大的GM+VW、GG+VW组合。总之,FN+RW+VW或PL+VW组合是共性误差剔除后坐标时间序列噪声特性的最优表示模型。
3.2.3噪声分量大小
共性误差剔除前的最优噪声组合FN+VW与PL+VW的相应噪声分量见表1,两者可变白噪声分量及有色噪声分量近似相等。
共性误差剔除后最优噪声组合FN+RW+VW与PL+VW的相应噪声分量见表2,两种噪声模型估计的白噪声大小同样近似。
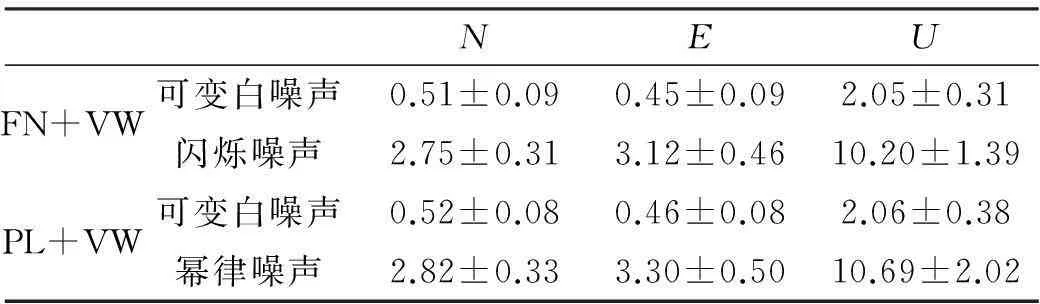
表1 共性误差剔除前最优噪声模型噪声分量均值
注:可变白噪声单位为mm,闪烁噪声单位为mm/,幂律噪声单位为mm/,为噪声幂指数。

表2 共性误差剔除后最优噪声模型噪声分量均值
对比共性误差剔除前后噪声分量的大小,为保证对比单位的统一性,选择共性误差剔除前的FN+VW组合与共性误差剔除后的FN+RW+VW组合进行对比。通过共性误差的剔除,坐标时间序列中的可变白噪声成分平均降低了22%、18%、17%,闪烁噪声成分平均降低了71%、72%、66%。顾及共性误差的功率谱特性,表明共性误差的剔除显著降低了坐标时间序列中的闪烁噪声,但对可变白噪声的降噪效果有限。
3.3测站速度及其精度
基于共性误差剔除前后最优噪声模型估计的ITRF2008框架下测站速度及其精度见表3。华北地区GPS连续基准站具有大体相等的水平速度,垂直速度差异较大,部分测站具有明显的沉降趋势(如YONQ、HECX及TJBH)。RW噪声的准确估计至少需要5 a以上的坐标时间序列[13],而本文中的坐标时间序列长度均不超过5 a,利用现有的坐标时间序列估计的噪声中RW成分是不准确的。因此,选择PL+VW噪声模型分析共性误差剔除后的坐标时间序列,计算速度及速度误差相对更准确。
表4给出了利用FN+VW噪声模型和PL+VW噪声模型计算共性误差剔除前后的测站平均速度误差与仅考虑VW噪声模型得到的测站平均速度误差对比。顾及有色噪声的影响,各测站水平向速度误差小于0.5 mm/a,垂向速度误差约为1.5 mm/a,测站速度误差比仅考虑随机噪声模型得到的误差大5~8倍,共性误差的剔除提高了速度精度,尤其是垂向速度精度提高至1 mm/a以下,为研究区域地壳形变提供了高精度的速度场信息。
4 结 语
1)利用区域堆栈滤波方法提取华北地区GPS基准站坐标时间序列中的共性误差,进行频谱分析发现,共性误差具有类似闪烁噪声的特性。从坐标时间序列中剔除共性误差,能够有效降低坐标时间序列的噪声水平,同时有效提高测站坐标序列拟合的速度精度,精度提高40%左右,说明对区域GPS坐标时间序列进行共性误差剔除是十分必要的。
2)利用极大似然估计方法分析坐标时间序列的噪声特性,发现共性误差剔除前的坐标时间序列噪声特性可以由FN+VW或PL+VW噪声组合模型描述,共性误差剔除后的坐标时间序列噪声特性可以由FN+RW+VW或PL+VW噪声组合模型描述。共性误差的剔除使得具有全局分布特征的FN噪声成分降低70%左右,可变白噪声降低20%左右,并使得具有站点效应的RW噪声成分部分显现出来。但是,由于坐标时间序列时长的限制,测站的RW噪声无法准确估计,有待后续更长的坐标时间序列进行分析。
3)考虑有色噪声计算的测站平均速度误差比仅考虑白噪声误差大5~8倍,说明单纯可变白噪声模型下的速度拟合高估了计算速度的精度,在分析微小地壳运动时,可能会导致误判。因此,对区域GPS坐标时间序列的共性误差进行滤波处理和噪声分析,对利用GPS基准站数据获取高精度的地壳形变特征很有必要。
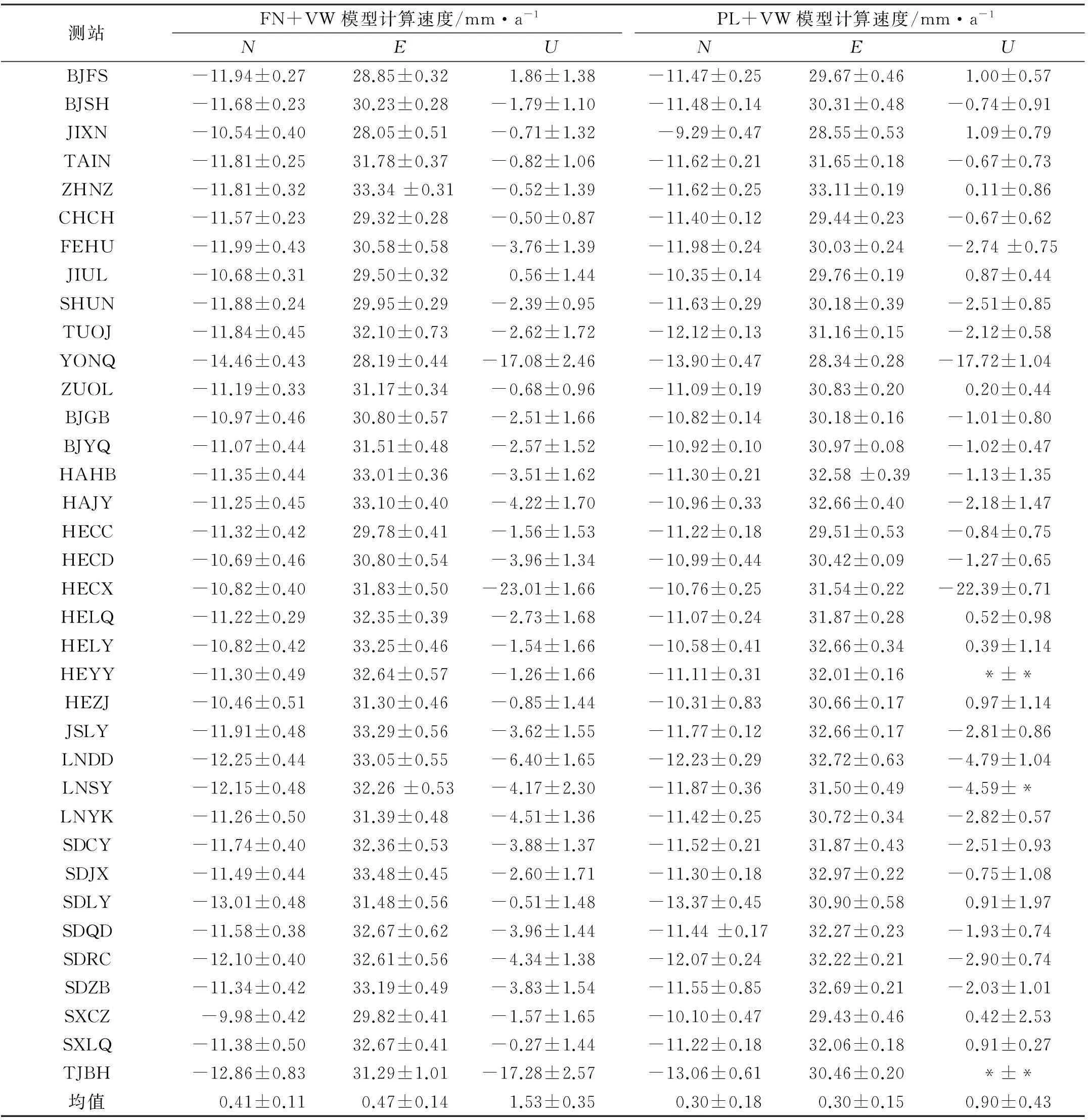
表3 共性误差剔除前后最优噪声模型计算的ITRF2008测站速度及其精度
注: *表示无法成功进行极大似然估计。

表4 平均速度误差对比
注: 速度误差单位为mm/a。
参考文献
[1]Wdowinski S, Bock Y, Zhang J, et al. Southern California Permanent GPS Geodetic Array: Spatial Filtering of Daily Positions for Estimating Coseismic and Postseismic Displacements Induced by the 1992 Landers Earthquake[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B8): 18 057-18 070
[2]Zhang J, Bock Y, Johnson H, et al. Southern California Permanent GPS Geodetic Array: Error Analysis of Daily Position Estimates and Site Velocities[J]. Journal of Geophysical Research, 1997, 102(B8): 18 035-18 055
[3]袁林果, 丁晓利, 陈武, 等. 香港GPS基准站坐标序列特征分析[J]. 地球物理学报, 2008, 51(5): 1 372-1 384(Yuan Linguo, Ding Xiaoli, Chen Wu, et al. Characteristics of Daily Position Time Series from the Hong Kong GPS Fiducial Network [J], Chinese Journal of Geophysics, 2008, 51(5): 1372-1384)
[4]Williams S D P, Bock Y, Fang P, et al. Error Analysis of Continuous GPS Position Time Series[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B3)
[5]牛之俊, 马宗晋, 陈鑫连, 等. 中国地壳运动观测网络[J]. 大地测量与地球动力学, 2002, 22(3): 88-93(Niu Zhijun, Ma Zongjin, Chen Xinlian, et al. Crustal Movement Observation Network of China[J].Journal of Geodesy and Geodynamics, 2002,22(3):88-93)
[6]Nikolaidis R. Observation of Geodetic and Seismic Deformation with the Global Positioning System[D]. San Diego: University of California, 2002
[7]Dong D, Fang P, Bock Y, et al. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen-Loeve Expansion Approaches for Regional GPS Network Analysis[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B3)
[8]Dach R, Brockmann E, Schaer S, et al. GNSS Processing at CODE: Status Report[J]. Journal of Geodesy, 2009, 83(3-4): 353-365
[9]伍吉仓, 孙亚峰, 刘朝功. 连续 GPS 站坐标序列共性误差的提取与形变分析[J]. 大地测量与地球动力学, 2008, 28(4): 97-101(Wu Jicang, Sun Yafeng, Liu Chaogong. Extraction of Common Mode Errors for Continuous GPS Networks and Deformation Analysis[J].Journal of Geodesy and Geodynamics, 2008, 28(4):97-101)
[10]Agnew D C. The Time-Domain Behavior of Power-Law Noises[J]. Geophysical Research Letters, 1992, 19(4): 333-336
[11]Mao A, Harrison C G A, Dixon T H. Noise in GPS Coordinate Time Series[J]. Journal of Geophysical Research: Solid Earth, 1999, 104(B2): 2 797-2 816
[12]黄立人. GPS 基准站坐标分量时间序列的噪声特性分析[J]. 大地测量与地球动力学, 2006, 26(2): 31-34(Huang Liren. Noise Properties in Time Series of Coordinate Component at GOS Fiducial Stations[J]. Journal of Geodesy and Geodynamics,2006, 26(2):31-34)
[13]Langbein J. Noise in GPS Displacement Measurements from Southern California and Southern Nevada[J]. Journal of Geophysical Research Solid Earth, 2008, 113(B5):620-628
[14]Williams S D P. CATS: GPS Coordinate Time Series Analysis Software[J]. GPS Solutions, 2008, 12(2): 147-153
[15]Santamaría-Gómez A, Bouin M N, Collilieux X, et al. Correlated Errors in GPS Position Time Series: Implications for Velocity Estimates[J]. Journal of Geophysical Research: Solid Earth, 2011, 116(B1):384-398
Foundation support:International Science and Technology Cooperation Program of China,No.2015DFR21100; National Key Basic Research Program of China, No.2013CB733304; National Natural Science Foundation of China, No.41461164004,41404023,41174004; Open Fund of Shanghai Space Navigation and Positioning Technology Key Laboratory, No.201401.
About the first author:WU Weiwei, PhD candidate, majors in high-precision GPS data processing and current crustal deformation, E-mail: 14_jasonwu@tongji.edu.cn.
收稿日期:2015-08-10
第一作者简介:吴伟伟,博士生,研究方向为GPS数据处理与现今地壳形变,E-mail:14_jasonwu@tongji.edu.cn。 通讯作者:孟国杰,研究员,研究方向为地壳形变与地球动力学,E-mail: mgj@cea-ies.ac.cn。
DOI:10.14075/j.jgg.2016.08.012
文章编号:1671-5942(2016)08-0708-06
中图分类号:P228
文献标识码:A
Corresponding author:MENG Guojie, professor, majors in crustal deformation and geodynamics, E-mail: mgj@cea-ies.ac.cn.
Noise in GPS Coordinate Time Series for North China Fiducial Stations
WUWeiwei1,2MENGGuojie2WUJicang1
1College of Surveying and Geo-Informatics, Tongji University, 1239 Siping Road, Shanghai 200092, China2Institute of Earthquake Science, CEA, 63 Fuxing Road, Beijing 100036, China
Abstract:We assess the characteristics of noise in the coordinate time series of daily position from August 2008 to April 2013 at 36 north China GPS fiducial stations. Regional stacking filtering is employed to remove the common mode errors from the daily position time series. The noise characteristics of time series and the station velocities are assessed using maximum likelihood estimation. The results indicate that the common mode errors are attributed to the flicker noise and that their variations are 1 mm for the NS component, 1 mm for the EW component and 3 mm for the vertical component. The noise in the unfiltered position time series can be described as a combination of variable white noise plus flicker noise or variable white noise plus power-law noise, while the filtered position time series can be described as a combination of variable noise plus flicker noise plus random walker noise or variable white noise plus power-law noise. The removal of the common mode errors decreases the flicker noise component and highlights the corresponding noise component related to site effects. The velocity uncertainties are about 5-8 times greater than if only variable white noise is considered. The velocity uncertainties decrease by about 40% if the common mode errors are removed.
Key words:daily position time series; stacking filter; maximum likelihood estimation; noise characteristics; velocity uncertainty
项目来源:国家国际科技合作专项(2015DFR21100);国家973计划(2013CB733304);国家自然科学基金(41461164004,41404023,41174004);上海市空间导航与定位技术重点实验室开放基金(201401)。

