连续介质弹性悬臂梁动态响应的仿真模拟实现

汤　萍，王三海

(1.安徽水利水电职业技术学院，安徽 合肥 231603；2.安徽江淮汽车集团，安徽 合肥 230022)



连续介质弹性悬臂梁动态响应的仿真模拟实现

汤萍1，王三海2

(1.安徽水利水电职业技术学院，安徽 合肥 231603；2.安徽江淮汽车集团，安徽 合肥 230022)

目的通过理论求解、实验、仿真模拟等方法分别对连续介质弹性悬臂梁的振动振型及固有频率进行研究，探讨各方法的优劣和互补，确定仿真计算在连续介质弹性悬臂梁的振动振型及固有频率的可行性。方法对连续介质弹性悬臂梁建立可解的力学分析模型，推导出连续介质弹性梁的振型方程和固有频率方程，选取梁的前3阶固有频率，得出理论的固有频率值；建立实验模型，通过实验方法，得出实验的固有频率值；以实验模型为参考建立仿真计算模型，再得出计算的固有频率值。结果在前3阶固有频率值中统计得出：实验值最低、理论值次之、仿真计算值最高。将3种方法的结果进行对比误差分析，后2种方法与实验值误差在合理范围内。结论仿真计算由于强约束性、系统刚度增大，导致固有频率增大，使用中结合实验模型，适当修正约束刚度，可以更好接近实验值，对研究连续介质系统的动态响应是强有力的补充或替代。

连续弹性梁；固有频率；仿真模拟

1　引　言

系统的振动问题几乎贯穿所有的工程结构和运动机构，可能导致零部件的磨损和松脱、疲劳强度的降低、动力的损耗、噪声的增加、结构的破坏等，从而影响结构或机构的物理性能、动力特性、使用安全和寿命。弹性悬臂梁作为常见的工程结构，学者们试图采用多种手段对其振动进行研究[1-5]，随着计算机的高速发展，诸如有限元方法等计算研究也已经深入这个领域[1-5]，使研究的方法更加多样，可选择的手段更加丰富。其中使用如ADAMS、RECURDYN、COSMOS等动力学仿真软件进行振动的仿真模拟并结合实验手段、理论研究等一体化研究方法，正日益成为运动机构振动问题研究的潮流和方向[6-9]。

动力学仿真软件MSC.ADAMS具有强大的建模、运动模拟、数据分析和结构优化能力，借助有限元前处理网格生成程序对刚体进行弹性化处理，可以进行刚-弹混和结构的动力学仿真，使得软件的适用范围得到极大的拓宽[10]。本文基于MSC.ADAMS软件对连续介质弹性悬臂梁的振动问题进行研究，在软件中建立悬臂梁的激振系统模型，并参考实验模型设置仿真参数，期望得到悬臂梁的动力特性响应，并与实验研究的结果进行对比验证，由此总结实验模型研究的计算模拟再现的思路和方法。

2　连续弹性悬臂梁的振动分析

一维连续系统的振动可归结为一维杆纵向波动方程，其解包含2个：1个对应描述含固有频率的简谐振动的频率方程；另1个定义杆的纵向振动形态的振型方程，即所谓的模态函数，一般是以杆轴线为坐标的振幅百分比值。理论上，连续系统固有频率有无限多个，第i阶固有频率设为ωi，其对应模态函数设为φi(x)，由此可以得到以ωi为固有频率，φi(x)为模态函数的一维杆系统纵向振动的主振动方程。

u(i)(x,t)=αiφi(x)sin(ωit+θi)(i=1,2,…)

(1)

对于连续介质系统，上式可写成

(2)

其中ωi，qi(i=1,2,…)由系统初始条件确定。

考虑等截面矩形细直梁(图1)，以未变形时的轴线为x轴，以梁对称面内垂直于x轴的方向为y轴，只研究欧拉-伯努利梁的振动。梁做平面弯曲振动，其载荷图及单元分析图如图2所示。

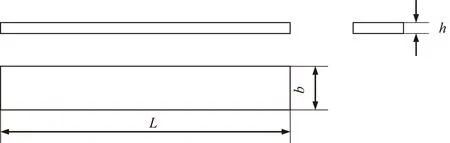
图1　等截面矩形细直梁

图2　载荷图及单元分析图

根据微元体平衡方程及弹性理论，得等截面梁弯曲振动方程：

(3)

若梁自由振动，f(x,t)=0,式(4)即为第i阶固有频率及对应模态函数的主振动方程：

y(i)(x,t)=αiφi(x)sin(ωit+θi)(i=1,2,…)

(4)

考虑到连续介质系统，其自由振动方程由无数多的主振动叠加组成，则(4)式变为

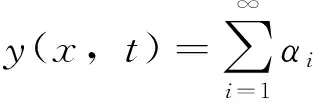
(5)

其中ωi，qi(i=1,2,…)由系统初始条件确定。由悬臂梁的约束状态及边界方程

(6)

代入(5)式可解得频率方程及模态函数

cosβlchβl+1=0

(7)

φ(x)=cosβix-chβix+ξi(sinβix-shβix)(i=1,2,…)

(8)

利用数值计算等方法解出

(9)

式中：βil—频率方程cosβlchβl+1=0的解，前5个根βil(i=1,2,3,…)依次为1.875，4.694，7.855，10.995，14.137，…

其中，E—材料弹性系数(Pa)，A—梁横截面积(m2)，ρl—材料线密度(kg·m-1)，ρl=ρA

ρ—材料密度(kg·m-3)，I—梁截面弯曲惯性矩(m4),对矩形截面，I=bh3/12(m4)，B为梁横截面宽度(m)，h为梁横截面高度(m)。

3　实验及计算模型

3.1实验模型及数据

实验中利用钢尺代替弹性悬臂梁如图1所示，l=310 mm，b=26 mm，h=0.9 mm，E=20×1011Pa，ρ=7 800 kg·m-3。根据式(9)计算可得各阶固有频率理论值之比：

f1∶f2∶f3∶f4∶f5……=1∶6.27∶17.55∶34.389∶56.842:…，f1=7.6Hz

前三阶固有频率f1=7.6，f2=47.65，f3=133.4

(10)

当给梁施加一个周期性的激振力，且该激振力的频率正好等于梁的某阶固有频率，就会产生共振，对应于这一阶固有频率确定的振动形态叫做该阶主振型，此时其它各阶振型的影响小到可以忽略不计。采用共振法，连续调节激振力的频率，当梁出现某阶主振型且振动幅值最大即产生共振时，就可认为此时的激振力频率是梁的这一阶固有频率。利用此方法，得出实验钢尺(连续弹性悬臂梁)的各阶固有频率的实验数据分别为6 Hz、37 Hz、103 Hz。

3.2计算模型及数据

利用实验钢尺的尺寸参数在ADAMS软件中建立仿真模拟计算模型。考虑到悬臂梁的弹性，首先在软件中按尺寸建立刚性梁模型，然后导入ANSYS软件，对刚性梁模型进行网格划分，生成ADAMS软件可用的模态中性文件(*.mnf)，再用ADAMS/Flex模块将刚性梁弹性化，得到连续弹性悬臂梁计算模型，如图3所示。

在钢尺与振动台的连结点处施加沿垂直振动方向一致的移动约束，并添加振动激励-正弦函数0.5*sin(fi*2*pi*time)，fi为激振频率，当观察到共振状态时，结合振型图，此时的fi值即为梁该阶振型的固有频率。

经计算，得模拟计算固有频率分别为8.2、51.4、144.2 Hz。

综合实验研究、仿真模拟计算、理论求解，分别得到悬臂梁的前3阶固有频率如表1。

图3　连续弹性悬臂梁计算模型

阶次i123振型固有频率理论值(Hz) 7.647.7133.4固有频率实验值(Hz) 6.037.0103.0固有频率仿真模拟计算值(Hz)8.251.4144.2

由表1中结果可知，实验方法、仿真模拟计算方法所求的前3阶固有频率与理论值均有误差，仿真计算值更接近理论值。通过前述所知，理论值是用近似公式计算的，本身就是数值解，而不是解析解，仿真计算基本还原了理论值的数值求解过程，两者的结果理应最接近，但由于在建仿真计算模型时，可能连接点位置确定的悬臂梁长度与给定参数不一致，由式(9)可知，将会导致结果的较大误差。同样道理，实验装置不能保证安装后的悬臂梁长度就是给定的理论参数值，并且固定端约束较仿真计算模型柔性大，其实验值与仿真计算值的误差真实地反映在表中。

4　结　论

综上所述，仿真模拟计算是数值迭代计算的结果，与悬臂梁的理论计算值很接近，而且建模过程兼具实验的特性，能反映出理论模型与实验模型的细微差别，并在计算结果中得以表现。所以仿真计算可以作为实验方法研究连续弹性梁的强有力的补充手段，并将日益成为主流方法。

[1]周丹.用Solidworks和ANSYS对微硬盘悬臂梁进行建模及模态分析[J].机械制造与自动化,2009,(06):180-183.

[2]杨笑冬.基于ANSYS的悬臂梁模态分析[J].机电一体化,2008,(06):58-60.

[3]赵振宇,卢荻,丑修建,等.硅基反铁电薄膜微悬臂梁力学仿真分析[J].测试技术学报,2010,(05):444-448.

[4]刘权等.基于LabVIEW的悬臂梁固有频率测试研究[J].电子测量技术，2009,32(09):85-88.

[5]刘俊等.ADAMS柔性体运动仿真分析研究及运用[J].现代制造工程，2004，(05):53-55.

[6]包日东,冯颖,郝敏.不同支承条件下梁结构弯曲振动的固有特性[J].机械设计与制造,2009,(09):83-85.

[7]赵峰，曹树谦，冯文周.干摩擦悬臂梁一阶等效固有频率研究[J].振动与冲击，2015,34(10):46-49.

[8]吴伟明,郭春鹏.基于Solidworks的摩托车灯HS1固有频率分析[J].中国照明电器，2014,(10):22-26.

[9]杨帅，王太勇.竖直方向弹性约束悬臂梁的固有频率分析[J].天津大学学报，2011,44(01):18-22.

[10]叶志才，孙立国.水闸结构抗震分析的悬臂梁振型分解反应谱法[J].河海大学学报，2009,37(04):437-440.

[责任编辑：冯浩英文编辑：刘彦哲]

Implementation of Simulation of Dynamic Responses to Continuum Elastic Beam

TANG Ping1,WANG San-hai2

(1.Anhui Technical College of Water Resources and Hydroelectric Power，Hefei,Anhui 231603，China；2.Anhui Jianghuai Automobile Group，Hefei,Anhui 230022,China)

ObjectiveBy respectively using theoretical method,experiment method and simulation method,vibration mode and natural frequency of the continuum elastic cantilever beam were studied,and the advantages and disadvantages of complementary methods were discussed to determine the feasibility of the simulation calculation of vibration mode.MethodsFirstly,a mechanical analysis model of the continuum elastic beam was established,the vibration equation and frequency equation of the beam were derived,and the first three natural frequencies of the beam were selected as the inherent frequency of the theoretical value;secondly,by experimental method,the experimental value was drawn;finally,a simulation model was built based on the experimental model,and the inherent frequency value was calculated.ResultsIn the first three-order natural frequency values obtained by three kinds of methods,the experimental value was lowest,which was next to the theoretical one,and the simulation value was highest.And both of experimental natural frequency value error and simulation value error were more reasonable than another method.ConclusionDue to the strong constraints and the increased system stiffness,simulation increases frequency.Experimental model with modified constraint stiffness can better close to the experimental values,which is a strong complement or alternative to the dynamic response of the continuum system.

continuum elastic beam；natural frequency；simulation

10.3969/j.issn.1673-1492.2016.05.003

安徽省教育厅省级质量工程模具专业综合改革试点项目资助(皖教高[2014]18号，2014zy113)

汤萍(1973-)，女，安徽桐城人，高级工程师，硕士。研究方向：机械设计与制造。

TH 11

A

来稿日期：2015-12-24