理论研究连接方式对低聚(3-己基噻吩)结构和电子光谱的影响
马 原,左桂云,吴文鹏*
(1.河南大学 化学化工学院,环境与分析科学研究所,河南 开封 475004; 2.河南大学 民生学院,河南 开封 475004)
理论研究连接方式对低聚(3-己基噻吩)结构和电子光谱的影响
马原1,左桂云2,吴文鹏1*
(1.河南大学 化学化工学院,环境与分析科学研究所,河南 开封 475004;2.河南大学 民生学院,河南 开封 475004)
用密度泛函理论优化了不同连接方式的低聚(3-己基噻吩)((3HT)n,n=2~8)异构体的几何结构,并得到了相对能量,接着用含时密度泛函理论计算了不同异构体的垂直激发能,并优化了(3HT)8第一激发态的几何结构. 结果表明,不同连接方式异构体的相对能量接近,但它们的轨道能级和垂直激发能差异都较大; 第一激发态比基态共平面性更好.
聚(3-己基噻吩);连接方式;密度泛函理论;含时密度泛函理论
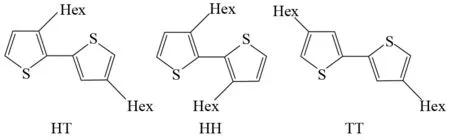
图1 P3HT中相邻噻吩环之间可能的连接方式Fig.1 Possible coupling ways between thiophene rings in P3HT
聚噻吩及其衍生物是一种重要的有机半导体材料,广泛应用在有机发光二极管[1]、有机太阳能电池[2]、有机场效应晶体管[3-4]等领域. 其中聚(3-己基噻吩)(P3HT)以其良好的稳定性、可溶解性[5],成为研究最多的体系之一. 噻吩的聚合反应发生在噻吩环的2-,5-位上,当有两个3-己基噻吩进行偶联时可能出现3种不同的连接方式(图1):头尾连接(head-to-tail, HT)、尾尾连接(tail-to-tail, TT)、头头连接(head-to-head, HH)[6-9],形成3种不同的异构体. 随着3-己基噻吩个数的增多,异构体数不断增大. 到目前为止,人们研究较多的是立构规整度高的纯HT连接的P3HT,而对其他异构体研究较少. 最近,CHU等[10]报道了用立构规整(regioregular)的P3HT和立构随机(regiorandom)的P3HT的混合物可以提高有机场效应晶体管的性能. 众所周知,结构决定性质. 因此有必要对P3HT的各种异构体的结构进行详细研究. 以前的研究[11-15]表明,密度泛函理论可以很好地预测分子的结构和光谱等性质. 因此,我们用密度泛函理论研究3-己基噻吩低聚物(3HT)n(n=2~8)不同异构体的性质.
1 计算方法
在B3LYP[16-17]/6-31G*水平上优化得到3-己基噻吩低聚物(3HT)n(n=2~8)基态的几何结构,并在相同理论水平下进行振动频率的计算. 用B3LYP/6-31+G**计算了各异构体的单点能和轨道能级. 它们的第一垂直激发能是在TD[18-19]-B3LYP/6-31+G**水平上计算得到的. 所有计算都是在Gaussian09程序包[20]中完成的.
2 结果与讨论
2.1基态的几何结构
根据以前的研究,聚(3-烷基噻吩)中硫原子处于异侧的反式构象比硫原子处于同侧的顺式构象稳定[9],因此本工作只考虑了反式构象. 同时,由于烷基链不是本研究的重点,本工作未考虑己基内部的可能构象. 由于随着噻吩环个数的增大,异构体数迅速增多,我们只能选择一部分进行研究. 对n=2~4,我们分别计算了3、4和5种可能构象;对n=5~8,我们计算了3种构象. 优化得到的(3HT)n(n=2~8)不同异构体的基态的主要键长r和噻吩环之间的扭转角D列于表1和表2中. 其中,C-C键指噻吩环之间相连的C-C键,扭转角用相邻噻吩环之间的二面角D(S-C-C-S)表示. 从表1和表2中可以看出,HT、TT和HH 3种连接方式中C-C键长分别在0.145 1~0.145 8、0.144 7~0.145 1和0.146 1~0.146 6 nm范围内,扭转角分别在134°~149°、157°~180°和102°~118°之间. TT连接方式中噻吩环之间C-C键的键长是最短的,扭转角最接近平面,其次是HT连接方式,最后是HH连接方式. 因此TT连接方式中环之间的共平面性最好,体系的共轭程度最强;HH连接方式中己基之间较强的空间位阻效应使两相邻噻吩环偏离平面程度最大,共轭性最差. 对立构规整的纯HT体系来说,越靠近链中间,共轭程度越大. 几何结构的这些变化必将影响它们的能级特征和电子吸收光谱性质,这在下一步的计算中将会得到验证.
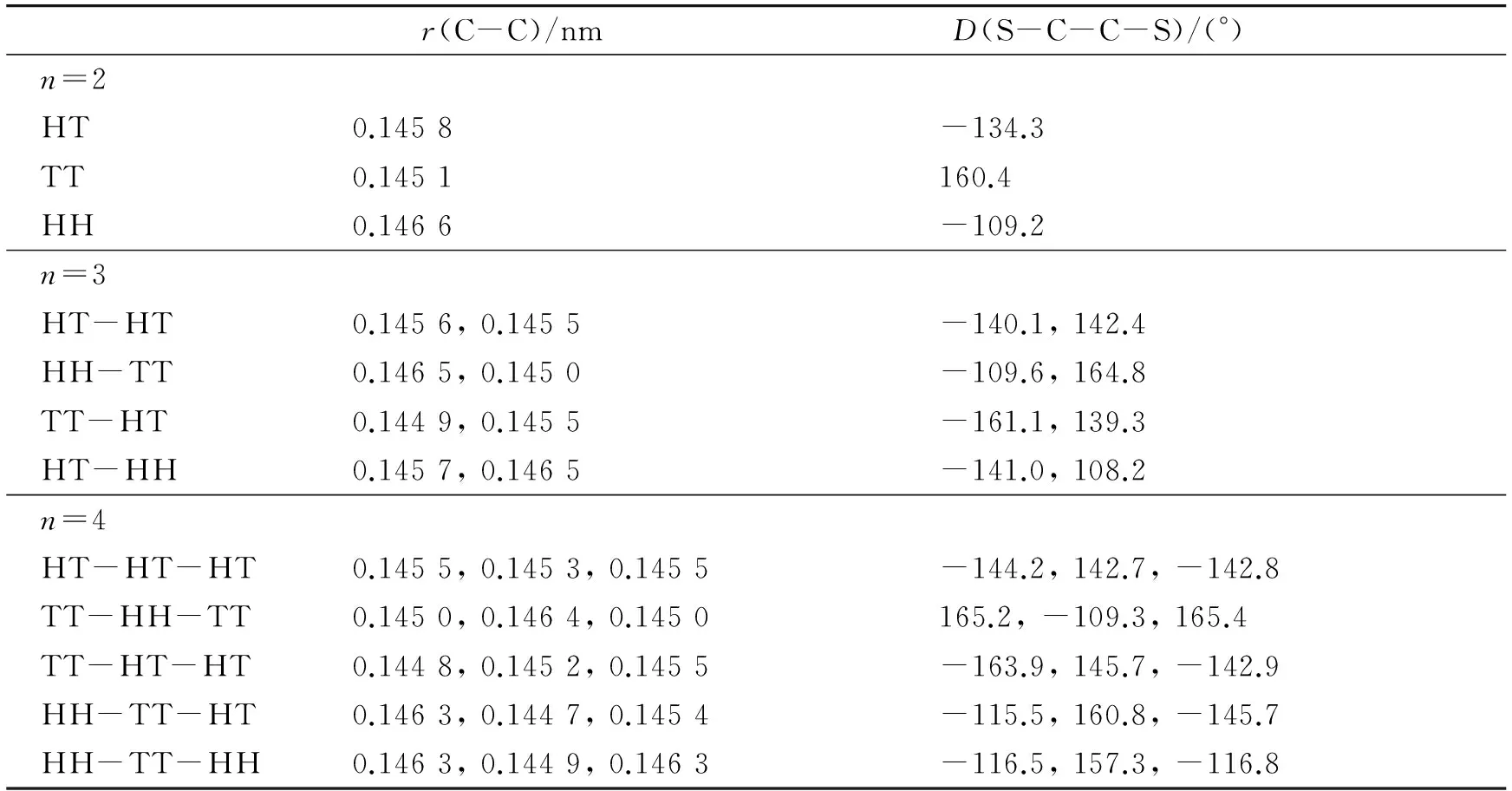
表1 (3HT)n(n=2~4)的主要键长和扭转角
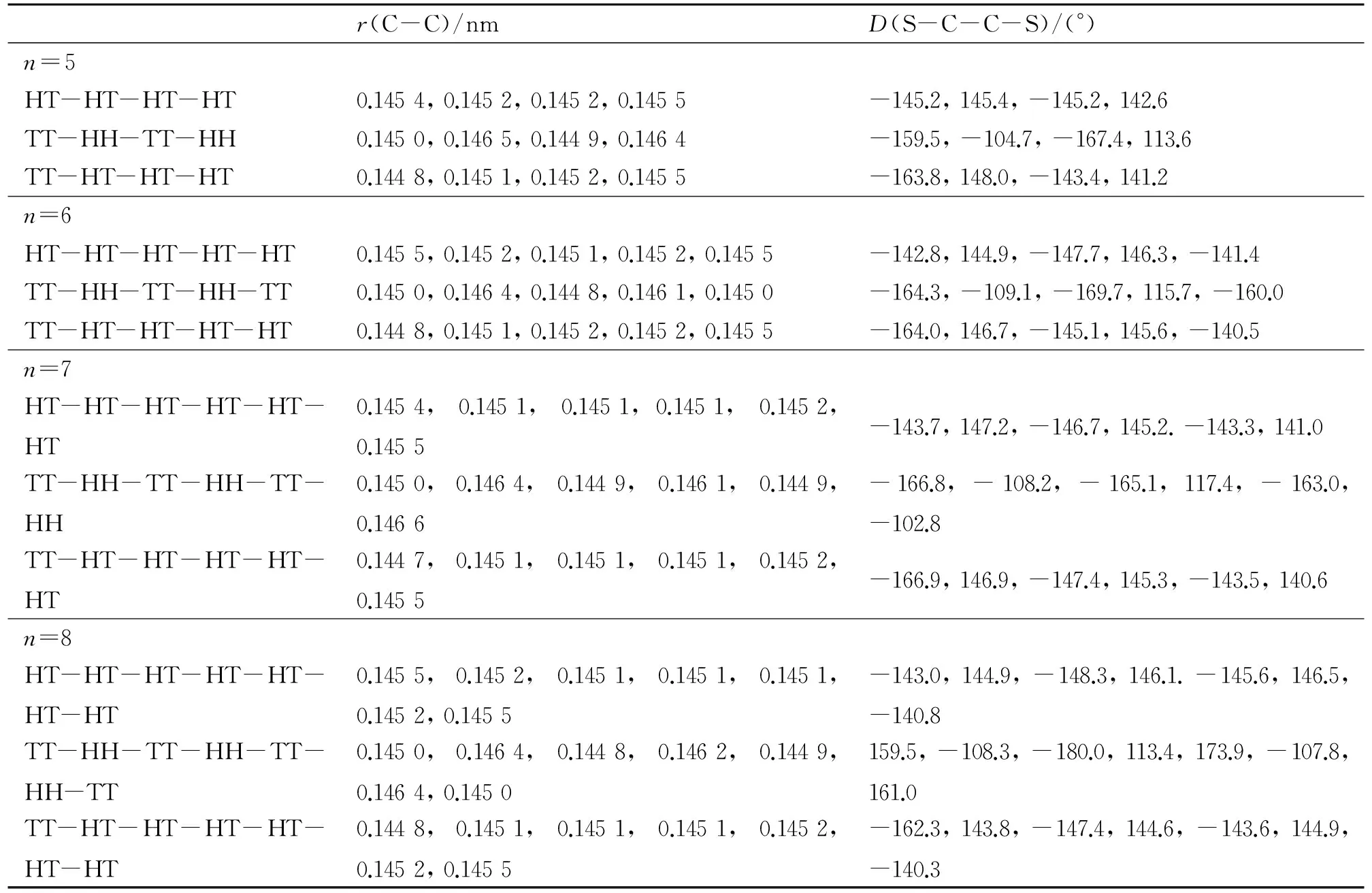
表2 (3HT)n(n=5~8)的主要键长和扭转角
2.2垂直激发能
计算得到的各低聚物的相对能量列于表3中. 从表3可以看出,立构规整的纯HT体系相对能量不是最低的,但各不同异构体之间能量相差不大,在不控制实验条件的状况下都有可能生成,这与实验上得到的立构随机产物相一致.
分子的电子吸收光谱的性质与前线分子轨道密切相关,计算发现这些体系的第一激发态主要都来自于最高占据轨道(HOMO)到最低空轨道(LUMO)的跃迁,而且吸收强度最大,因此我们将各体系的HOMO、LUMO能级、HOMO-LUMO能级差ΔEg、第一垂直激发能ΔEv及相应的吸收波长λ和振子强度f列于表3中. 对n=2,TT异构体的HOMO能级最高,LUMO能级最低,ΔEg、ΔEv最小,λ最长,f最大,HH异构体恰好相反,HT异构体居中. 这可以从几何结构上进行解释: TT中两己基链相距最远,空间位阻最小,两噻吩环共轭程度最强;而HH中两己基链相距最近,空间位阻最大,两噻吩环共轭性最差. 对n=3~8,每一个体系中的第3个异构体(即端基为TT,其余为HT)的吸收波长最长,振子强度最大,对光的吸收性能最好. 但随着噻吩环个数的增多,该异构体与纯HT的异构体吸光性能之间的差距越来越小,当n=8时,两者几乎一样. 这与实验上纯HT连接的P3HT异构体吸光性能最好相一致. 随着n的增大,对于同一类型的体系(如纯HT连接,或TT-HH间隔连接),HOMO能级逐渐升高,LUMO能级逐渐降低,ΔEg、ΔEv逐渐减小,λ逐渐增长,f逐渐增大,对光的吸收性能增强. 因此,体系越长,共轭程度越大,越有利于光的吸收.

表3 (3HT)n(n=2~8)的一些物理参数
同时,我们研究了第一垂直激发能和HOMO-LUMO能级差之间的关系. 通过拟合所计算的24种分子的ΔEv和ΔEg,得到了一条直线(见图2),ΔEv=0.946 81ΔEg-0.199 37. 相关系数为0.995 69,标准偏差为0.051 57,线性关系良好. 因此,可以通过直接计算ΔEg,利用该公式就可以推算出ΔEv,而不用再进行垂直激发能的计算.
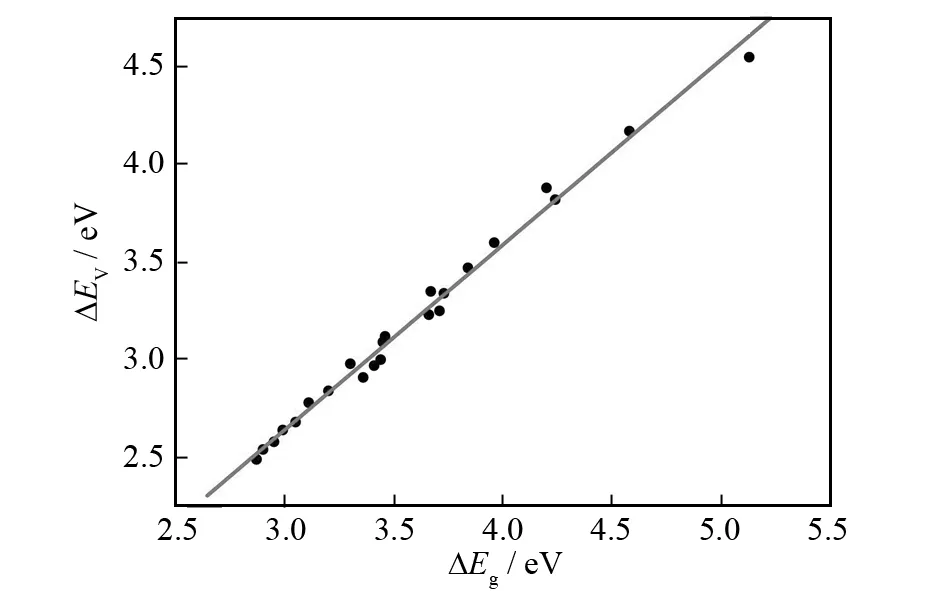
图2 ΔEv和ΔEg之间的线性拟合图Fig.2 Linear fit between ΔEv and ΔEg
2.3激发态的几何结构
为了了解分子在受到光激发后以及失去一个电子后几何结构的变化,我们对立构规整的(3HT)8的第一激发态(S1)和阳离子态(Cation)的几何结构进行了优化,结果列于表4中. 比较表2和表4中数据可以发现,从基态到S1态,连接噻吩环之间的C-C键键长缩短,变化最大的为中间的C-C键,缩短了0.0037 nm,扭转角明显增大,中间部分接近平面;阳离子结构变化类似. 因此,从基态到激发态或者阳离子态,分子的共面性增强,共轭程度增大,有利于电荷的转移.
3 结论
用密度泛函理论优化得到了低聚(3-己基噻吩)体系各异构体基态的几何结构,计算显示,HT、TT和HH 3种连接方式中C-C键长分别在0.145 1~0.145 8、0.144 7~0.145 1和0.146 1~0.146 6 nm范围内,扭转角分别在134°~149°、157°~180°和102°~118°之间. 各不同异构体的能量相差不大. 用含时密度泛函理论计算得到了各低聚物异构体的垂直激发能,结果表明,立构规整的纯HT异构体的垂直激发能比HH-TT间隔排列的异构体的小,吸收波长更长,振子强度更大,对光的吸收性能更好. 通过对第一垂直激发能和HOMO-LUMO能级差的拟合,得到了一个线性关系,利用该关系就可以用HOMO-LUMO能级差来推算第一垂直激发能. 最后,我们优化了第一激发态和阳离子态的几何结构,发现第一激发态和阳离子态比基态共面性更好,更有利于电荷的传输和转移,另外,对不同异构体混合后的性能研究正在进行中.

表4 (3HT)8S1态和阳离子态的主要键长和扭转角
[1] PEREPICHKA I F, PEREPICHKA D F, MENG H, et al. Light-emitting polythiophenes [J]. Adv Mater, 2005, 17(19): 2281-2305.
[2] WANG H J, CHEN C P, JENG R J. Polythiophenes comprising conjugated pendants for polymer solar cells: a review [J]. Materials, 2014, 7(4): 2411-2439.
[3] ASSADI A, SVENSSON C, WILLANDER M, et al. Field-effect mobility of poly(3-hexylthiophene) [J]. Appl Phys Lett, 1988, 53: 195-197.
[4] SON S Y, KIM Y, LEE J, et al. High-field-effect mobility of low-crystallinity conjugated polymers with localized aggregates [J]. J Am Chem Soc, 2016, 138(26): 8096-8103.
[5] PATIL A O, HEEGER A J, WUDL F. Optical properties of conducting polymers [J]. Chem Rev, 1988, 88: 183-200.
[6] DANG M T, HIRSCH L, WANTZ G, et al. Controlling the morphology and performance of bulk heterojunctions in solar cells. Lessons learned from the benchmark poly(3-hexylthiophene):[6,6]-phenyl-C61-butyric acid methyl ester system [J]. Chem Rev, 2013, 113: 3734-3765.
[7] SOUTO MAIOR R M, HINKELMANN K, ECKERT H, et al. Synthesis and characterization of two regiochemically defined poly(dialkylbithiophenes): a comparative study [J]. Macromolecules, 1990, 23: 1268-1279.
[8] MAO H, XU B, HOLDCROFT S. Synthesis and structure-property relationships of regioirregular poly(3-hexylthiophene) [J]. Macromolecules, 1993, 26: 1163-1169.
[9] MCCULLOUGH R D, LOEW R D, JAYARAMAN M, et al. Design, synthesis, and control of conducting polymer architectures: structurally homogeneous poly(3-alkylthiophenes) [J]. J Org Chem, 1993, 58: 904-912.
[10] CHU P H, WANG G, FU B Y, et al. Flexible OFETs: Synergistic effect of regioregular and regiorandom poly(3-hexylthiophene) blends for high performance flexible organic field effect transistors [J]. Adv Electron Mater, 2016, DOI: 10.1002/aelm.201670010.
[11] 宁攀, 赵建想. 利用密度泛函理论研究α-联噻吩体系H(C4H2S)nH的结构和电子光谱[J]. 化学研究, 2013, 24(5): 493-500.
[12] 李洁琼, 赵清岚. 三种席夫碱-Ni(Ⅱ)配合物的电子结构和吸收光谱的理论计算[J]. 化学研究, 2014, 25(5): 497-503.
[13] 吴文鹏, 曹艳. 三(4-硝基苯基)甲烷衍生物的结构和振动光谱的理论研究[J]. 化学研究, 2014, 25(6): 609-615.
[14] 李洁琼, 李永红. 用密度泛函理论研究两种金属镍席夫碱配合物的电子结构和光谱性质[J]. 化学研究, 2014, 25(6): 616-621.
[15] 李云飞, 王新收, 吴文鹏. 一种基于苯并噻二唑衍生物的F-荧光探针分子的理论研究[J]. 化学研究, 2015, 26(6): 575-578.
[16] BECKE A D. Density-functional thermochemistry. III. The role of exact exchange [J]. J Chem Phys, 1993, 98(7): 5648-5652.
[17] LEE C, YANG W, PARR R G. Development of the Colic-Salvetti correlation-energy formula into a functional of the electron density [J]. Phys Rev B, 1988, 37: 785-789.
[18] FURCHE F, AHLRICHS R. Adiabatic time-dependent density functional methods for excited state properties [J]. J Chem Phys, 2002, 117: 7433-7447.
[19] SCALMANI G, FRISCH M J, MENNUCCI B, et al. Geometries and properties of excited states in the gas phase and in solution: Theory and application of a time-dependent density functional theory polarizable continuum model [J]. J Chem Phys, 2006, 124: 094107 1-15.
[20] FRISH M J, TRUCKS G W, SCHLEGEL H B, et al. Gaussian 09 [CP]. Revision A.02, Wallingford CT: Gaussian, Inc., 2009.
[责任编辑:张普玉]
Effect of coupling ways on the structures and electronic spectra of oligo(3-hexylthiophene): a theoretical investigation
MA Yuan1, ZUO Guiyun2, WU Wenpeng1*
(1.InstituteofEnvironmentalandAnalyticalSciences,CollegeofChemistryandChemicalEngineering,HenanUniversity,Kaifeng475004,Henan,China; 2.MinshengCollege,HenanUniversity,Kaifeng475004,Henan,China)
Density functional theory was used to optimize the geometries of oligo(3-hexylthiophene) ((3HT)n,n=2-8) isomers with different coupling ways, and the relative energies were obtained. Then time dependent density functional theory were employed to calculate their vertical excitation energies and to optimize the geometry of the first excited state of (3HT)8. It shows that the relative energies of different isomers are close to each other, but their orbital energies and vertical excitation energies are different. Furthermore, the first excited state is more coplanar than the ground state.
poly(3-hexylthiophene); coupling ways; density functional theory; time dependent density functional theory
1008-1011(2016)04-0450-05
2016-06-06.
河南大学博士科研启动基金(B2013141),河南大学科研基金项目(2015YBZR009).
马原(1992-), 女, 硕士生, 研究方向为理论与计算化学.*通讯联系人, E-mail:wuwp@henu.edu.cn.
O641
A

