海上浮式风电机半潜式平台二阶水动力计算与响应特性分析
彭春江 胡燕平 程军圣 沈意平
1.湖南大学汽车车身先进设计制造国家重点实验室,长沙,4100822.湖南科技大学,湘潭,411201
海上浮式风电机半潜式平台二阶水动力计算与响应特性分析
彭春江1,2胡燕平2程军圣1沈意平2
1.湖南大学汽车车身先进设计制造国家重点实验室,长沙,4100822.湖南科技大学,湘潭,411201
提出了基于二次脉冲响应函数法的海上浮式风电机浮式平台二阶水动力计算方法,该方法基于三维势流理论用直接积分法求浮式平台的二次传递函数,并结合波高时程,将二次脉冲响应函数法应用于浮式平台二阶水动力的计算。把计算所得二阶水动力施加到海上浮式风电机整机时域动力学计算模型,计算二阶水动力的激励响应。以DeepCwind半潜式平台为算例,其上支撑美国可再生能源实验室5MW参考风机。先对所提出的二阶水动力计算方法进行验证,再分别在无风和有风条件下,计算一阶水动力单独激励响应和一阶二阶水动力共同激励响应,通过对比响应幅值谱、响应统计值,分析二阶水动力的激励特性。结果表明,对于半潜式平台,慢漂力和平均漂移力有明显的激励作用,和频二阶水动力的激励作用可以忽略。
海上浮式风电机;半潜式平台;二阶水动力;二次传递函数;响应特性
0 引言
为了开发水深超过60 m海域的风资源,在海上风电机组中配置固定式基座不再经济可行,因此提出了用浮式平台支撑风电机。浮式平台由于受到波的激励作用,其水动力特性相比固定式基座复杂得多,这使得浮式风电机整机动力学特性更加复杂。因此浮式平台水动力特性是海上风电技术研究的一个重要方面,而建立浮式平台水动力计算模型是浮式平台水动力研究的重要内容之一,是研究浮式风电机整机动力学特性的基础。
二阶水动力包括差频及和频二阶水动力,差频二阶水动力又包括平均漂移力和慢漂力。对于传统海上浮式结构,二阶水动力相比一阶水动力小一个数量级以上,对于海上浮式风电机,二阶水动力相比气动力更小,且存在气动阻尼,因此,目前对海上浮式风电机浮式平台水动力计算,只考虑一阶水动力,忽略了二阶及以上的水动力[1]。但Goupee等[2]和Koo等[3]在风、浪水池中,对海上浮式风电机进行模型测试,发现二阶水动力相比一阶水动力和气动力虽然很小,但在不同的风浪环境下,能激起浮式平台的特征模态,产生共振响应,影响海上浮式风电机的运行性能和系泊系统的疲劳寿命。因此,在海上浮式风电机浮式平台水动力计算中考虑二阶水动力是必要的。
López-Pavón等[4]、Coulling等[5]根据二次传递函数和波高时程,用纽曼近似法计算浮式平台的二阶水动力。纽曼近似法计算简单,有计算时间短的优势,但只有当浮体的固有频率很低且处在深水海域时计算出的二阶水动力才是有效的,而用二次脉冲响应函数法求平台的二阶水动力是一种相对直接的方法,虽然计算时间比纽曼近似法要长,但计算结果更接近试验测试数据[6],且没有应用范围的约束,更具通用性。
Karimirad[7]利用传统海上结构物时域非线性动力学计算程序计算风电机浮式平台的二阶水动力响应,计算中把风轮简化为风盘进行简单的风力计算,这样得到的二阶水动力响应与实际情况相差较大。Roalda等[1]、Bayati等[8]在频域根据二次传递函数直接求海上浮式风电机浮式平台二阶水动力响应,由于频域计算不能考虑瞬态响应过程,只能得到二阶水动力的稳态响应。而基于海上浮式风电机整机动力学计算模型,在时域计算浮式平台二阶水动力响应更符合实际情况。
因此,本文基于三维势流理论用直接积分法求浮式平台的二次传递函数,结合波高时程,将二次脉冲响应函数法应用于海上浮式风电机浮式平台二阶水动力计算,在海上浮式风电机整机时域动力学计算模型的基础上,计算浮式平台在各种环境激励下的响应,通过对比响应幅值谱、响应统计值,分析二阶水动力的激励特性。
1 二阶水动力计算
描述浮式风电机浮式平台的运动及载荷需定义两个坐标系:①惯性参考坐标系OXYZ,其中X轴为顺风向,Z轴沿风电机塔架轴线垂直向上,原点O为Z轴与平均海平面(MSL)的交点,Y轴方向由右手定则确定;②平台随体坐标系O′X′Y′Z′,在未扰动位置时与OXYZ重合,该坐标系随平台的移动改变原点位置,随平台的转动改变方向。原点O′在惯性参考坐标系OXYZ中的三个坐标分量即为风电机浮式平台的三个平移量,X′相对X轴、Y′相对Y轴、Z′相对Z轴的转动量即为平台的三个转动量,原点O′为浮式平台的计算参考点。定义与X方向一致的波向和风向为0°波向和风向。图1为坐标系的示意图。

图1 参考坐标系
本文水动力计算理论中的几个假设:①入射波的幅值比波长小得多,这就允许使用简单的入射波运动学理论,如线性波理论;②相比浮式平台的大小(也即平台的特征长度),浮式平台的运动量很小,这样,利用势流理论,在平台未扰动位置计算得到的水动力可以施加在扰动后平台的计算参考点;③浮式平台是刚性的;④平稳海况下波面高度是呈高斯分布的随机过程,且是线性的。
1.1不规则波波高时程计算
在不规则海况,根据假设①和④,波高时程可以用高斯白噪声过程经过线性滤波得到。本文所用实现方法是,在频域用Box-Muller法计算高斯白噪声过程,在给定海浪谱的前提下,根据平稳线性系统输入输出功率谱关系求得波高的频域表示,通过傅里叶反变换求得波高时程。
在浮式平台参考点处,不规则波的波高可表示为有随机相位的规则波之和:
(1)
式中,ζi为单个规则波的波幅;ωi为波频率;εi为相位。
在本文中ζ(0,0,0,t)简写为ζ(t),ζ(t)用高斯白噪声过程经过线性滤波得到:
(2)
式中,w(τ)为均值为0、标准差为1的高斯白噪声随机变量;h(t)为线性滤波传递函数。
在频域根据平稳线性系统输入输出功率谱关系,经傅里叶反变换可求得波高ζ(t)为
(3)
式中,S2-Sided(ω)为波高的双侧功率谱;W(ω)为w(τ)的傅里叶变换。
W(ω)用Box-Muller法计算得到:
1.2二阶水动力计算
二阶水动力的计算方法是先基于三维势流理论,用直接积分法求出海上浮式风电机浮式平台的二次传递函数,再对二次传递函数进行双重傅里叶反变换求得二次脉冲响应函数,最后在时域,利用二次脉冲响应函数与波高的双重卷积求总的二阶水动力。实现方法是在频域中根据波高和二次传递函数求出二阶水动力,再进行傅里叶反变换求时域二阶水动力。
利用势流理论,对浮体湿表面进行直接压力积分获得二阶水动力的通用表达式为
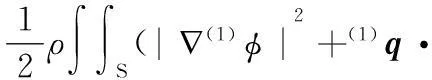
(4)
其中,变量中的上标(1)、(2)分别表示一阶量、二阶量,为哈密顿算符,M为浮体的质量矩阵,q为浮体平移位移矩阵,为浮体平移加速度矩阵,Ω为浮体角位移矩阵,WL表示水线,S表示湿表面,n为湿表面面元的外法线向量,(1)φ、(2)φ为速度势,ζrel为相对水线的波高。式(4)的前三项都是一阶解的二次作用,根据一阶解可全部确定,最后一项与二阶速度势有关,可用势流理论确定。式(4)的表达不方便计算,因此基于式(1)的波高表示,经推导,总二阶水动力可表示成如下形式:
(5)
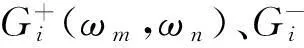
根据二次传递函数求二次脉冲响应函数gi(t1,t2):
在时域用二次脉冲响应函数计算总二阶水动力为
(6)
2 数值计算
本文根据式(6)用数值计算方法实现对和频、差频二阶水动力的求解。首先对时间和频率进行离散,在频域根据波高和二次传递函数计算每一离散频率点的二阶水动力,再用离散傅里叶逆变换求得离散时间点上的二阶水动力,然后通过插值法求任意时刻的二阶水动力。
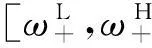
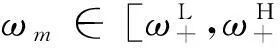
(7)
其中,m取小于N/4的全部正整数,其余频率点补零。第二项和频二阶水动力频域离散值:
(8)
其中,k取小于m/2的全部正整数。
通过离散傅里叶逆变换求得时域离散值分别为
(9)
(10)
其中,IDFT{}表示离散傅里叶逆变换。和频二阶水动力时域离散值为
(11)
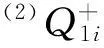

图2 和频二阶水动力计算流程
(12)
差频二阶水动力的非零频分量也称慢漂力,其频域离散值为
(13)
其中,k取小于N/2-m的所有正整数。
慢漂力的时域离散值为
(14)
(15)
差频二阶水动力的计算流程与和频二阶水动力的相似,这里就不再给出。
3 算例与分析
3.1计算对象与参数
基于以上二阶水动力计算理论,结合浮式风电机整机时域动力学计算模型,针对支撑美国可再生能源实验室(NREL)5MW参考风机[9]的DeepCwind半潜式平台[10]进行各种响应计算,浮式平台外形如图3所示,结构尺寸如表1所示,质量属性参数如表2所示,6个自由度的固有频率如表3所示,风机的性能尺寸详见文献[9]。本文计算方法同样可应用于风电机其他浮式平台。

图3 DeepCwind半潜式平台及风电机示意图

表1 半潜式平台结构尺寸 m
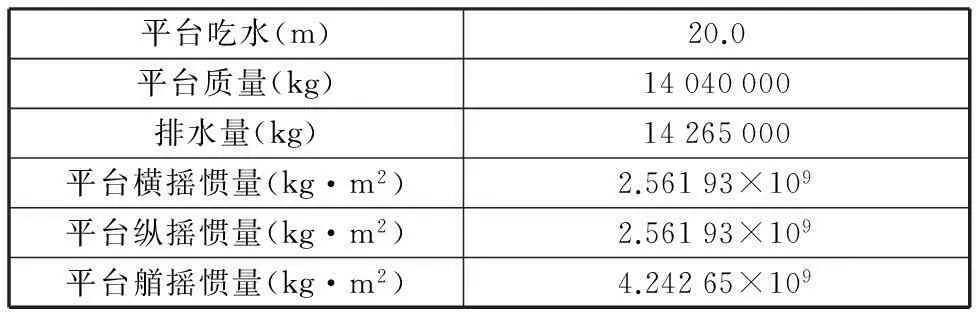
表2 半潜式平台质量参数

表3 半潜式平台6个自由度的固有频率
浮式平台水动力计算选用单向不规则波模型,采用JONSWAP波谱,波向与平台纵荡方向一致,表4所示为本文计算选用的3种波况。有效波高Hs的值4.5 m、7.1 m、11.8 m分别代表中等、严峻、极限三种海况。图4所示为所用3种有效波高的波谱S(ω),图5所示为Hs=7.1 m时平台参考点处的波高时程ζ(t)。从波谱图可知,有效波高不同,一阶波频区间稍有不同,为了减少二阶水动力计算量,根据一阶波频区间确定差频、和频二阶水动力的计算范围如表5所示。由表3可知,半潜式平台6个自由度的固有频率都处于中等海况一阶波频区间之外的低频段。对于严峻和极限海况,垂荡固有频率处于一阶波谱区间。
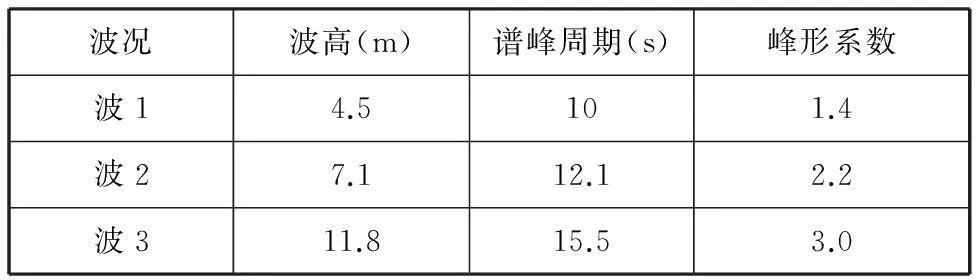
表4 计算波况(JONSWAP谱)

图4 有效波高分别为4.5 m、7.1 m、11.8 m的JONSWAP谱
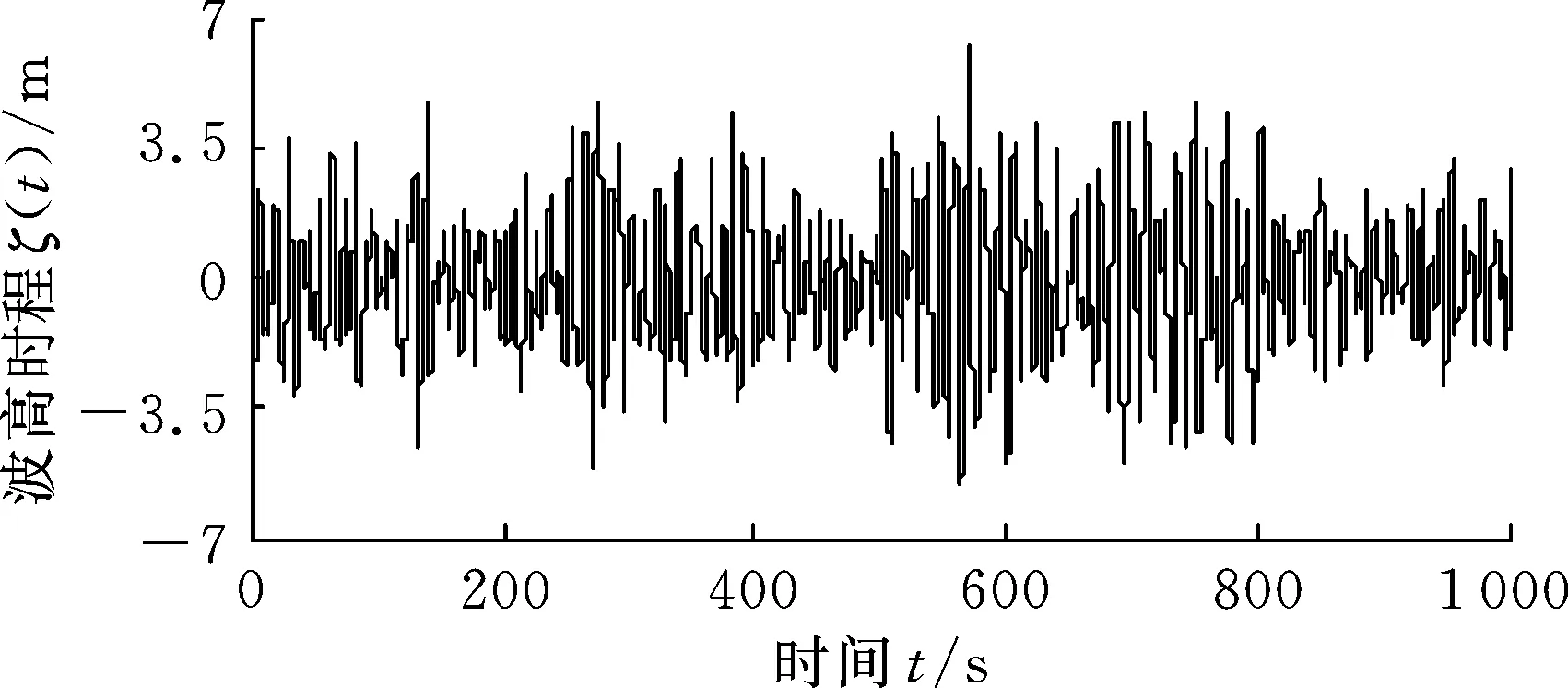
图5 有效波高为7.1 m时参考点处的波高时程

表5 二阶水动力计算频率范围 Hz
为了深入理解波频作用,排除湍流风低频激励作用的影响,选用稳态风进行激励,计算风速8 m/s、16 m/s、23 m/s分别代表风机额定风速以下、额定风速以上、临近切出风速时的风况。风向与波向一致,也即0°风向。
浮式风电机整机动力学计算的气动载荷模型采用叶素动量定理,考虑轮毂、叶尖损失。结构动力学建模采用凯恩方法结合模态叠加法,系泊系统采用准静态模型,一阶水动力计算模型参考文献[9],拖曳阻力采用莫里森公式中的拖曳项计算。水深200 m,平台吃水20 m,平台构件所用拖曳系数:主圆柱0.58,上圆柱0.61,基圆柱0.68,支架0.63。本算例中所使用的附加纵荡线性阻尼为1×106N/(m/s),附加横摇和纵摇线性刚度为1.45×109N·m/rad,附加纵荡二次阻尼为2.25×106N/(m/s)2,附加二次纵摇阻尼为5×106N·m/(rad/s)2。浮式平台响应计算时长为1000 s,取后500 s进行统计值计算。
3.2二阶水动力计算方法验证
文献[2-3]对本算例中的半潜式浮式风电机进行了1∶50比例模型风浪水池测试。图6所示为在无风波况2作用下,半潜式平台纵荡和纵摇响应功率谱Pi(ω) 的计算结果与试验结果。从图6可以看出计算结果与试验结果基本一致,这说明水动力(包括一阶和二阶)计算模型和方法是可行的。在低频段,纵荡和纵摇固有频率处的共振峰由差频二阶力激励所致,用本文二阶水动力计算方法很好地呈现了试验结果,这说明本文二阶水动力计算方法的正确性。

(a)纵荡响应功率谱

(b)纵摇响应功率谱图6 无风波况2作用下,一阶二阶水动力共同激励响应功率谱计算结果与测试结果
3.3响应计算与分析
本文针对以下两种激励条件,计算和分析二阶水动力对半潜式平台的激励响应:①无风只有波激励;②风、浪联合激励。对应海上浮式风电机的正常运行状态和生存状态,处于正常运行状态时受风、浪的联合激励,处于生存状态时风电机停机,风轮叶片顺桨,此时风大但风力小,主要受波力的作用,与无风只有波激励的情况相似。
3.3.1无风二阶水动力激励特性
图7所示为无风、波高为7.1 m时,一阶水动力单独激励与一阶二阶水动力共同激励下,平台各自由度的响应幅值谱Ai(ω)。从图7可知,在无风条件下,0°波向的二阶水动力在横摇固有频率处激起了明显的共振峰,但激励幅值很小,可视为无响应,考虑二阶水动力对横摇的影响无实际意义。横荡和艏摇也是如此,幅值谱就不再给出。对于纵荡和纵摇,一阶水动力在整个低频区间0~0.056 Hz有一定的激励幅值,在固有频率处甚至有幅值不大的一阶水动力共振峰。二阶水动力对整个低频区间的激励有所增强,在固有频率处激起了大幅值的共振峰。垂荡固有频率为0.058 Hz,处于一阶波频区间,从垂荡幅值谱可见一阶水动力在固有频率附近激励幅值较大。二阶水动力在整个低频区间对垂荡的激励都较弱。在波高为4.5 m和11.8 m的海况中,半潜式平台各自由度的响应幅值谱与波高为7.1 m海况的响应幅值谱相似,因此其他两种海况下的响应幅值谱不再给出。

(a)纵荡响应幅值谱
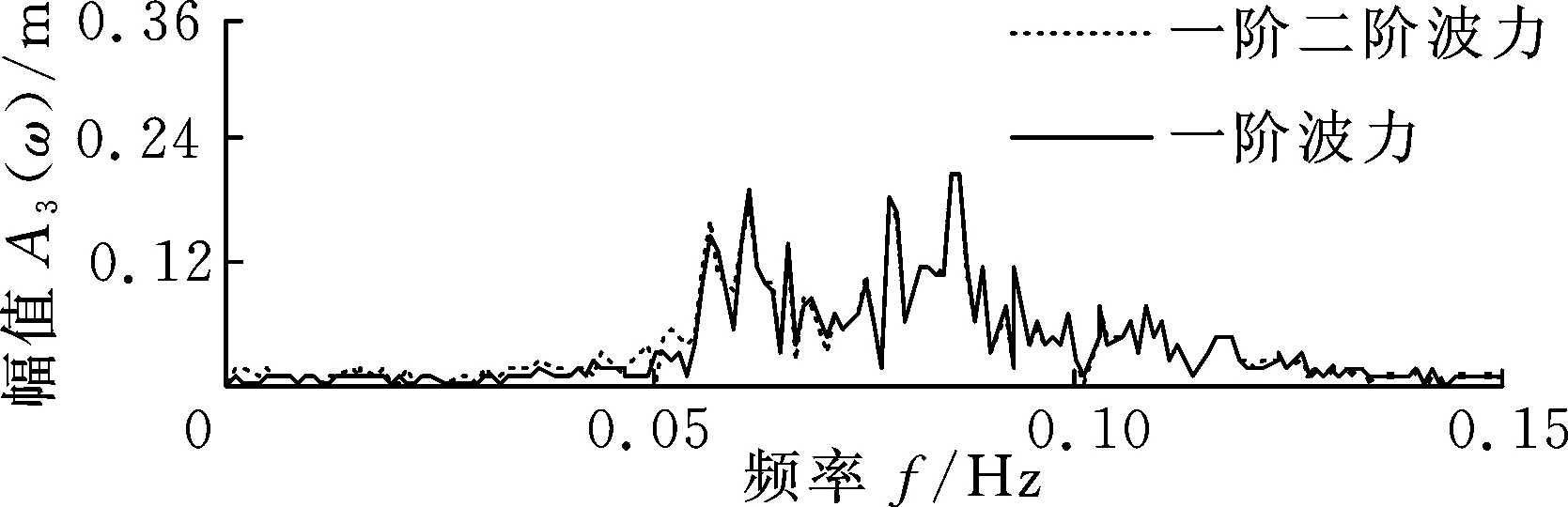
(b)垂荡响应幅值谱

(c)横摇响应幅值谱

(d)纵摇响应幅值谱图7 波高7.1 m、无风时,一阶水动力激励和一阶二阶水动力共同激励响应幅值谱
表6所示为无风条件下,波高分别为4.5 m、7.1 m、11.8 m时,一阶水动力单独激励和一阶二阶水动力共同激励平台各自由度响应均值和标准差。从表6可看出,一阶二阶水动力共同激励与一阶水动力单独激励响应之间存在均值差和标准差差值。均值差主要是平均漂移力激励所致,因此可用均值差衡量平均漂移力的激励作用。标准差可衡量响应的振荡幅值,用标准差差值衡量慢漂力的激励作用。
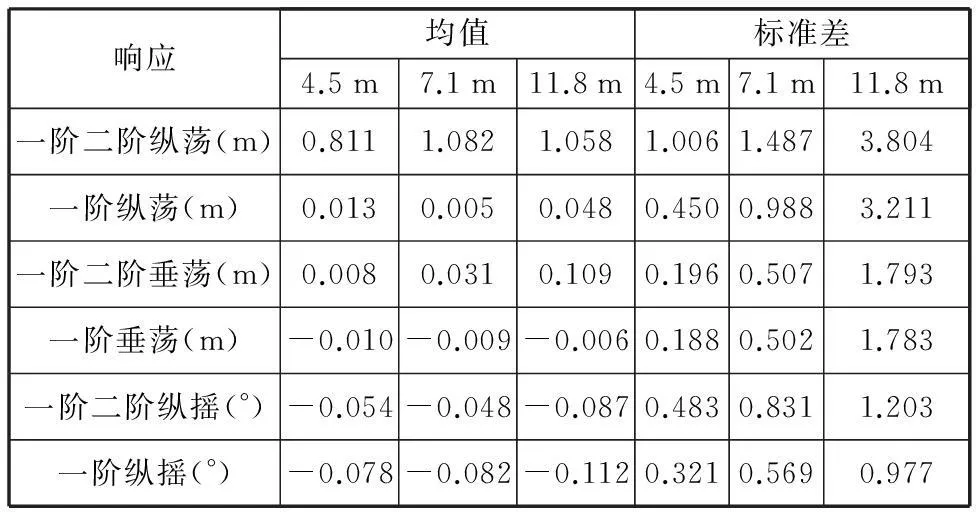
表6 无风不同波高条件下,平台一阶波激励与一阶二阶波共同激励响应统计值
表7所示为无风条件下,波高分别为4.5 m、7.1 m、11.8 m时,一阶水动力单独激励和一阶二阶水动力共同激励平台各自由度响应均值差和标准差差值。从表7可知,在三种海况下,平均漂移力会使纵荡响应发生较大的漂移,垂荡和纵摇响应的漂移值较小。各自由度响应均值差随波高变化,但不是单调的。纵荡响应标准差差值最大,纵摇次之,垂荡很小,这说明慢漂力对纵荡和纵摇可以激起较大的振荡幅值,对垂荡的激励作用很弱。标准差差值随波高变化,也不是单调的,因此平均漂移力和慢漂力对平台各自由度的激励作用会随波高变化,但不是单调的。
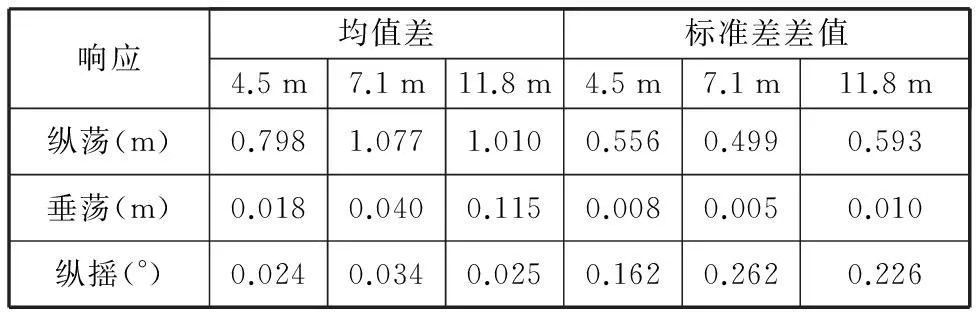
表7 无风不同波高情况下,平台一阶波激励与一阶二阶波共同激励响应均值差和标准差差值
3.3.2风浪联合作用下二阶水动力激励特性
图8所示为波高7.1 m、风速8 m/s时,一阶水动力单独激励和一阶二阶水动力共同激励下,平台各自由度响应幅值谱。从图8看到,在风浪联合作用下,一阶水动力在横摇固有频率附近激起了明显的共振峰,二阶水动力增强了共振峰,但幅值很小,横荡和艏摇的情况也是如此,相似的图就不再给出。
图8中,对于纵荡和纵摇,一阶水动力在整个低频段有一定的激励幅值,二阶水动力在固有频率附近出现了幅值不大的共振峰。对于垂荡,一阶水动力在0.058 Hz附近的激励幅值较大,这是固有频率处于一阶波频区间的缘故,二阶水动力在整个低频范围稍有增强激励幅值。对波高为7.1 m,风速分别为16 m/s、23 m/s,波高为4.5 m和11.8 m,风速分别为8 m/s、16 m/s、23 m/s的风浪联合激励响应幅值谱与图8相似,因此不再给出图。

(a)纵荡响应幅值谱

(b)垂荡响应幅值谱
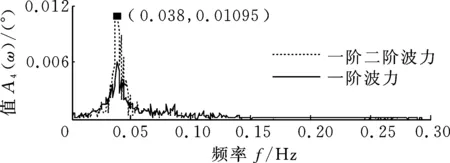
(c)横摇响应幅值谱

(d)纵摇响应幅值谱图8 波高7.1 m、风速8 m/s时,一阶水动力激励和一阶二阶水动力共同激励响应幅值谱
表8是波高为7.1 m,风速分别为8 m/s、16 m/s、23 m/s时,一阶水动力单独激励和一阶二阶水动力共同激励响应统计值。从表8可知,纵荡均值差在不同风速下约为1 m,随风速变化很小,垂荡和纵摇响应均值差不大,随风速基本不变。这说明平均漂移力对纵荡响应的影响较大,对垂荡和纵摇响应的影响较小,且基本上不受风速的影响。纵摇标准差在三种风速下分别为0.125、0.140、0.160,纵荡和垂荡的标准差差值比纵摇小一个数量级,且各自由度的标准差差值随风速变化很小。这说明在风浪联合作用下,慢漂力对半潜式平台各自由度的激励作用都较弱,且随风速变化基本不变。
表9是风速为8 m/s,波高分别为4.5 m、7.1 m、11.8 m时,一阶水动力单独激励和一阶二阶水动力共同激励响应统计值。从表9可知,纵荡、垂荡、纵摇均值差随波高变大,标准差差值总体来说都很小,随波高有变化,但不是单调的。这说明在风浪联合作用下,平均漂移力对纵荡、垂荡、纵摇的激励作用随波高变化,即波高越大,激励作用越强。

表8 波高7.1 m时,不同风速下一阶水动力激励和一阶二阶水动力共同激励响应均值差和标准差差值

表9 风速8 m/s时,不同波高下一阶水动力激励和一阶二阶水动力共同激励响应均值差和标准差差值
慢漂力对半潜式平台各自由度的激励作用都较弱,且随波高有相对较大的变化。
3.3.3其他激励特性对比
图9是波高4.5 m,无风和有风一阶二阶水动力共同激励下,半潜式平台纵荡和纵摇响应幅值谱,有风时的风速为8 m/s。从图9可知,对于纵荡和纵摇,有风条件下二阶水动力激励幅值相比无风时的要小很多,这是因为在有风条件下存在气动阻尼,抑制了二阶水动力的激励作用。

(a)纵荡响应幅值谱

(b)纵摇响应幅值谱图9 波高4.5 m,风速8 m/s,无风和有风一阶二阶波共同激励浮式平台自由度响应幅值谱
在有风条件下,本文计算的纵荡和纵摇响应幅值谱与文献[2]试验测得的响应谱有差别,文献[2]中气动阻尼几乎完全抑制了低频共振响应,而本文在低频段仍有较小的响应幅值,这是由于在计算模型中纵荡和纵摇阻尼过小造成的。
从图7、图8还可看出,在和频二阶水动力计算频率范围0.112~0.480 Hz,纵荡、垂荡及纵摇响应幅值谱几乎不受二阶水动力的影响,这说明在无风或有风条件下,和频二阶水动力对半潜式平台的激励作用可以忽略。
4 结论
本文针对海上浮式风电机,提出浮式平台二阶水动力的通用计算方法,并结合海上浮式风电机整机时域动力学计算模型。以支撑美国可再生能源实验室(NREL)5MW参考风机的DeepCwind半潜式平台为算例,在无风或有稳态风时,在一阶二阶水动力共同激励下,用本文计算方法计算的纵荡、纵摇响应谱与文献[2]试验测得的响应谱相近,验证了本文计算方法的可行性。
基于本文提出的计算方法,通过对算例的计算和分析,结果表明,对于半潜式浮式平台在本文计算条件下有如下结论:
(1)在无风或有风时,可忽略和频二阶水动力的激励作用,只考虑平均漂移力和慢漂力的激励作用。
(2)在无风时,慢漂力能激起纵荡和纵摇特征模态,产生低频共振响应,且响应幅值随波高变化。平均漂移力对纵荡的影响较大,对纵摇的影响较小,且随波高变化。
(3)在风浪联合激励下,由于存在气动阻尼,慢漂力在纵荡、纵摇固有频率附近的激励幅值明显受到了抑制,随风速基本不变,随波高有相对较大的变化。平均漂移力对纵荡的激励较强,对纵摇的激励较弱,随风速基本不变,随波高激励增强。
(4)在无风或有风时,二阶水动力对垂荡的激励作用都很弱。
[1]Roald L,Jonkman J,Robertson A,et al. The Effect of Second-order Hydrodynamics on Floating Offshore Wind Turbines[J]. Energy Procedia,2013,35:253-264.
[2]Goupee A J,Koo B,Kimball R W,et al. Experimental Comparison of Three Floating Wind Turbine Concepts[J]. Journal of Offshore Mechanics and Arctic Engineering, 2014,136(2):020906.
[3]Koo B,Goupee A J,Lambrakos K,et al. Model Tests for a Floating Windturbine on Three Different Floaters[J]. Journal of Offshore Mechanics and Arctic Engineering, 2014,136(2): 020907.
[4]López-Pavón C,Watai R A,Ruggeri F,et al. Influence of Wave Induced Second-order Forces in Semi-submersible FOWT Mooring Design[J].Journal of Offshore Mechanics and Arctic Engineering,2015,137(3):031602.
[5]Coulling A J,Goupee A J,Robertson A N,et al. Validation of a FAST Semi-submersible Floating Wind Turbine Numerical Model with DeepCwind Test Data[J]. Journal of Renewable and Sustainable Energy,2013,5(2):023116.
[6]Pinkster J A,Huijsmans R H M. The Low Frequency Motions of a Semi-submersible in Waves[C]//BOSS Conference.Cambridge,Massachusetts,1982:447-466.
[7]Karimirad M. Modeling Aspects of a Floating Wind Turbine for Coupled Wave-wind-induced Dynamic Analyses[J].Renewable Energy,2013,53:299-305.
[8]Bayati I,Jonkman J,Robertson A,et al. The Effects of Second-order Hydrodynamics on a Semisubmersible Floating Offshore Wind Turbine[R]. Golden,CO:The National Renewable Energy Laboratory (NREL),2014.
[9]Jonkman J M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine[D]. Fort Collins:Colorado State University,2001.
[10]Benitz M A,Schmidt D P,Lackner M A,et al. Comparison of Hydrodynamic Load Predictions between Engineering Models and Computational Fluid Dynamics for the OC4-DeepCwind Semi-Submersible[C]//The ASME 2014 33rd International Conference on Ocean,Offshore and Arctic Engineering. San Francisco,California,2014.
(编辑郭伟)
Second-order Hydrodynamics Computation and Response Characteristic Analysis for a Semi-submersible Offshore Floating Wind Turbine
Peng Chunjiang1,2Hu Yanping2Cheng Junsheng1Shen Yiping2
1.State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University,Changsha,410082 2.Hunan University of Science and Technology,Xiangtan,Hunan,411201
A second-order hydrodynamics computation method was proposed based on the quadratic impulse response function technique for offshore floating wind turbines. Firstly,the quadratic transfer functions were calculated using the direct integration method through three-dimensional potential theory. Secondly,the quadratic impulse response function technique was applied to compute the second-order hydrodynamics in terms of the quadratic transfer functions and wave elevation. Lastly,the resulting second-order hydrodynamics was acted on the integrated dynamics model of offshore floating wind turbine in time domain. So the excitation response of the second-order hydrodynamics might be computed. Taking the DeepCwind semi-submersible platform supporting the NREL 5-MW offshore baseline wind turbine for case,the verification of the second-order hydrodynamics computation method presented was conducted,and various excitation responses were calculated and analyzed. The results show the slow drift force and mean drift force have notable influences on semi-submersible platform,but the sum frequency second-order force can be neglected.
offshore floating wind turbine; semi-submersible floating platform; second-order hydrodynamics; quadratic transfer function; response characteristic
2015-05-21
国家自然科学基金资助项目(51075131,11572125)
TK83DOI:10.3969/j.issn.1004-132X.2016.07.018
彭春江,女,1977年生。湖南大学机械与运载工程学院博士研究生,湖南科技大学机电工程学院讲师。主要研究方向为海上浮式风力发电机组动力学及控制系统。胡燕平,男,1957年生。湖南科技大学机电工程学院教授、博士研究生导师。程军圣,男,1968年生。湖南大学机械与运载工程学院教授、博士研究生导师。沈意平,女,1982年生。湖南科技大学机械设备健康维护省重点实验室副教授、博士。

