基于响应曲面法的煤油发动机气门正时优化

张　伟　毛建国　魏特特　何小明

南京航空航天大学，南京，210016



基于响应曲面法的煤油发动机气门正时优化

张伟毛建国魏特特何小明

南京航空航天大学，南京，210016

利用基于仿真的响应曲面优化方法，对改型的煤油活塞发动机气门正时多目标优化问题进行了研究。建立了发动机性能仿真模型，以进气/排气正时、点火提前角为优化变量，以提高有效功率和降低燃油消耗率为设计目标进行了响应曲面优化。分析结果表明：相对于原汽油机，改型的煤油机进气门开启时刻要推迟，排气门关闭时刻要迟后，并且要提前一定的点火提前角，以得到最佳的发动机性能；同时，应用响应曲面法可以提升仿真优化的效率。

煤油发动机；数值模拟；响应曲面法；正时

0　引言

煤油在理化性质上，相比于汽油，具有闪点高、不易挥发的性质，而且密度比柴油小，同等质量下体积更小，所以其在安全、后勤保障方面有着重要地位[1]，以煤油为燃料的活塞发动机已成为研究热点。国内煤油活塞发动机起步较晚，正处于理论探索阶段，研究大多是在改型的汽机油的基础上进行的[2]。因此，在发动机的各个层面还需要根据煤油的特性进行改进设计、匹配优化。由于煤油具有燃烧速率比汽油低、不易蒸发等特点，其燃烧过程与汽油有很大不同，所以需要重新设计与之相匹配的换气过程，即需要对配气相位进行计算分析。

许多学者进行了发动机配气相位优化的相关工作，但大多是针对汽油、柴油机的，且优化方法上多是利用一般的配凑或直接法进行优化，优化方法不易实施且耗费很多计算时间。文献[3-5]将气门优化转化为单目标优化问题，而优化时仅由经验在仿真模型上试凑设计变量，优化结果受主观影响，且单目标无法考虑各个优化变量间的相互作用；文献[6-7]将仿真模型与优化算法直接耦合对配气相位进行优化，虽然可以得到准确的最优解，但耗费了大量的仿真计算时间；文献[8-10]采用DoE方法实现了对进排气参数的优化，但没有进一步结合响应曲面拟合算法，仍需要进行较多的仿真试验。

本文以某改型的煤油活塞发动机为研究对象，采用基于仿真的响应曲面优化方法对原气门正时进行了优化，改善了改型发动机的性能，同时将响应曲面法应用于优化中，提高了仿真优化的效率。

1　响应曲面法

响应曲面法(response surface methodology)是一种综合了统计学和数学并适用于产品开发、改进设计、优化处理的方法，最初应用于化学生产加工。随着其发展，响应曲面法被引入基于计算机仿真模型的优化中，利用响应曲面法建立仿真模型的近似模型，即元模型(metamodel)，然后在元模型上进行优化分析[11]。

响应曲面可以用下式表示：

y=f(β1,β2,…,βn,x1,x2,…,xk)+ε

(1)

式中，y为目标函数；xi(i=1,2,…,k)为设计变量；f为响应曲面模型，一般为多项式；ε为系统误差；βj(j=1,2,…,n)为未知参数。

建立响应曲面的过程就是利用回归分析方法对未知参数β进行估计的过程。

虽然直接利用高精度仿真模型进行优化可以获得准确可靠的优化方案，然而，当仿真模型十分复杂时，每次仿真计算都需要很长的计算时间，而且一次优化分析又需要调用数次仿真计算，耗费了大量时间资源。相对于一般的优化方法，响应曲面法可以反映设计参数和目标函数之间的关系。在充足的数据点和高精度回归方法的支持下，通过代数表达式可以形象地描绘出设计参数对目标函数的响应，因此在实际优化问题中，响应曲面法可以简化实际的复杂仿真模型，在保证必要精度的前提下，节省大量的仿真计算消耗，并能够完成优化任务[12]。

通常，基于仿真的响应曲面优化策略流程如图1所示。首先，选择试验设计，即由设计空间中较小数量的数据点实现获取信息最大化的方法[13]，得到一组具有代表性的初始设计点，并调用仿真模型计算这些设计点。然后对上述数据点进行统计分析，为特定的优化问题建立仿真模型的元模型[14-15]，即优化变量与目标变量的响应曲面。再验证所建立的响应曲面的有效性，如果精度不满足要求，则重新进行试验设计。得到可靠的响应曲面之后，就可以在响应曲面上利用优化算法搜寻最优解。最后将选定的最优解代入仿真模型进行评估[16]。

图1　基于仿真的响应曲面优化策略流程图

2　原型机GT-Power仿真模型

本文以某改型的进气道喷射四冲程煤油活塞发动机为研究对象(主要技术参数如表1所示，其中单位“°”表示曲轴转角)，利用一维CFD仿真软件GT-Power建立了该发动机的性能仿真模型，如图2所示。考虑气缸几何形状、混合气运动、燃料特性以及便于点火提前角调整，燃烧模型选取EngCylCombSITurb模型；为反映进气道喷射燃料在气道的积累、蒸发和向气缸传递的过程，进气道、排气道选取PipePort模型。

表1　原型机主要技术参数

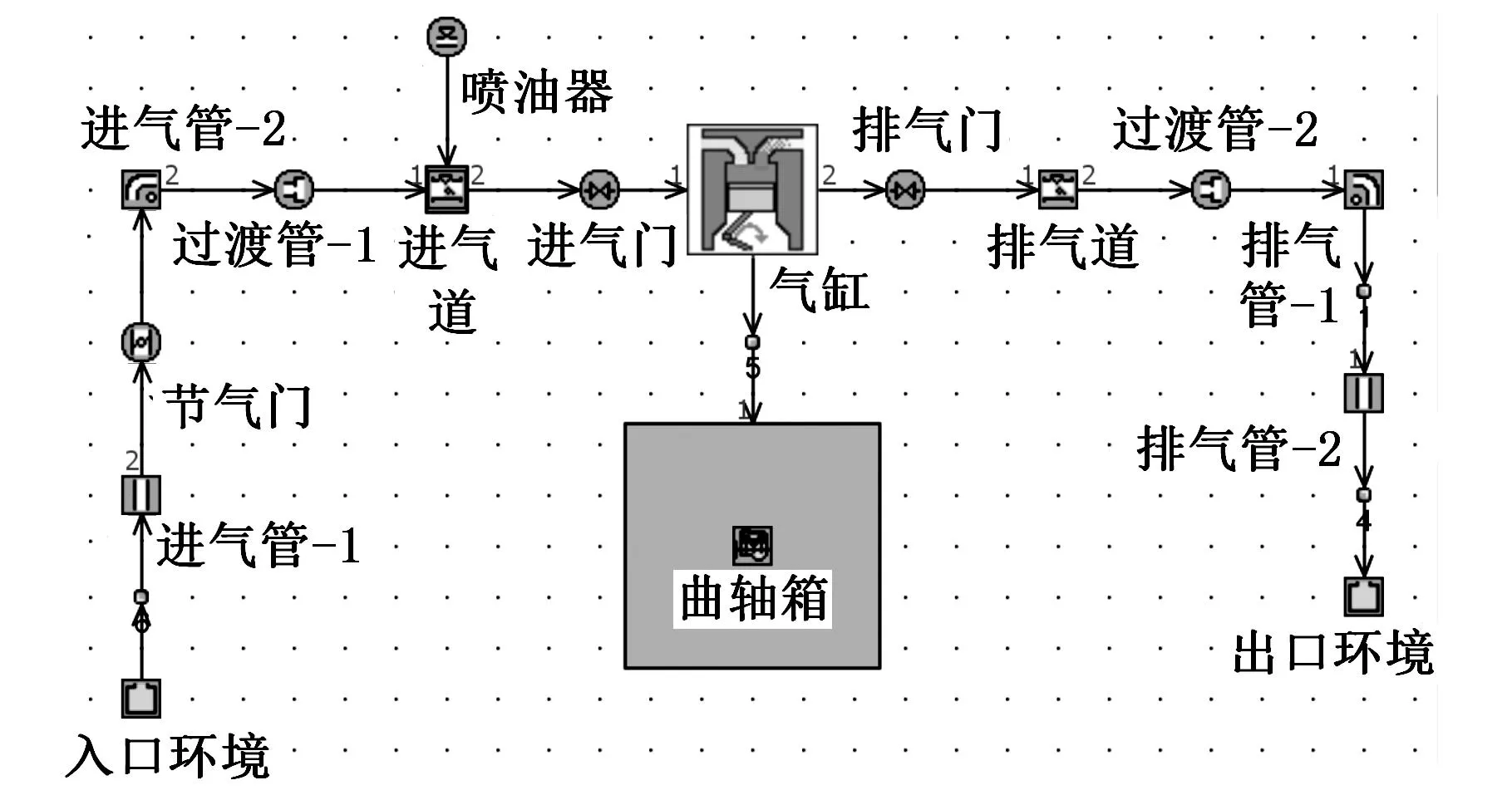
图2　原型机GT-Power模型

通过对比实验测取的不同转速(3000～5000 r/min)下，节气门开度为20%时的原型机缸内压力曲线，验证原型机GT-Power模型的有效性。

本文选取发动机转速为5000 r/min时的缸内压力对比曲线为例，如图3所示，仿真值曲线和实验值曲线基本吻合，燃烧段误差已远小于5%，达到了工程允许的误差范围，该模型可以用于原型机的仿真、优化任务。

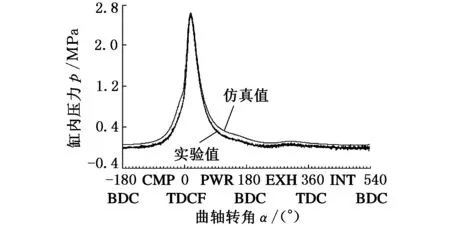
图3　5000 r/min时的缸内压力对比

3　基于响应曲面法的气门正时优化

本文采用基于仿真的响应曲面优化策略，借助专业优化软件modeFRONTIER(简称MF)，将其与GT-Power仿真模型耦合，在不改变进气门、排气门开启持续期的情况下，以进气提前角、排气迟闭角以及点火提前角(均指曲轴转角)为设计变量，以有效功率最大化、有效燃油消耗率最小化为目标进行优化。

3.1建立MF优化模型

整个优化策略的实现依托于在MF中建立的优化模型，如图4所示。

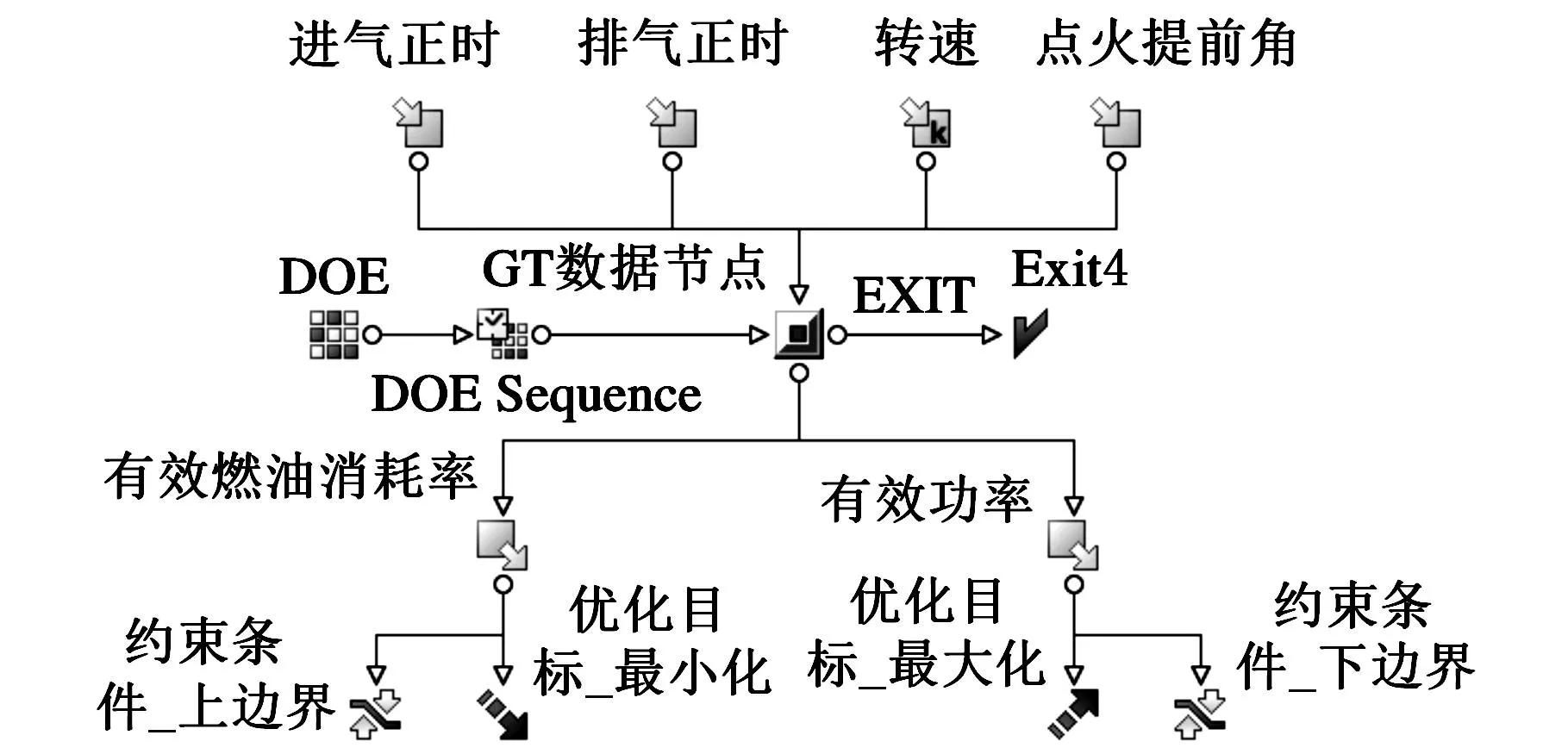
图4　MF优化模型

MF优化模型包括：①输入参数，即设计变量进气正时、排气正时、点火提前角，以及常量转速，因为原型机常用转速在4000～5000 r/min之间，所以优化时将转速恒定在4500 r/min；②输出参数，即优化目标有效功率、有效燃油消耗率以及相应的约束条件；③MF与GT-Power耦合的节点，以实现MF对GT-Power进行仿真计算的调度以及优化参数和仿真数据的传输；④逻辑调度节点，用于定义试验设计和优化调度算法，以确定优化计算分析的过程。优化模型中优化参数的边界及约束条件设置见表2。

表2　优化参数边界及约束条件的设置

3.2由试验设计生成初始数据点

建立基于仿真的响应曲面需要提供仿真模型的一系列具有代表性的仿真数据点，响应曲面的精度与这些仿真数据点的分布密切相关。因此，如何布置数据点对建立响应曲面至关重要[17]，即合适的试验设计是建立响应曲面的基础。相关学者提出了许多试验设计方法[11]，本文运用均匀拉丁超立方[18](uniform latin hypercube，ULH)方法进行试验设计，为响应曲面的建立提供初始数据点。ULH是一种常用的十分适用于仿真模型的空间填充技术(space-filling design)，可以在设计变量空间中生成分布相对均匀的数据点。对于n个设计点，k个变量的ULH，可以看成一个n×k的矩阵。每个变量Xi服从在其上下边界内的均匀分布，而矩阵的每一列相当于n个Xi的随机排列。

通常，仿真模型需要用二阶响应曲面模型简化。将k个设计变量的二阶响应曲面函数在点(x10，x20，…，xk0)处按泰勒级数展开，可以按x的幂次整理成如下形式：

(2)

式中，ε为系统误差；β为泰勒展开式中各项合并后的未知常数项。

由式(2)可以明确地看出其中包含1+2k+k(k-1)/2个未知参数β。因此，确定试验设计设计点的基本原则为必须至少有1+2k+k(k-1)/2个设计点；同时，设计中每个设计变量至少需要3个水平，以估计纯二次项[11]。本文有3个设计变量，所以需要生成33=27个初始设计点，图5所示为由ULH生成的设计变量空间。

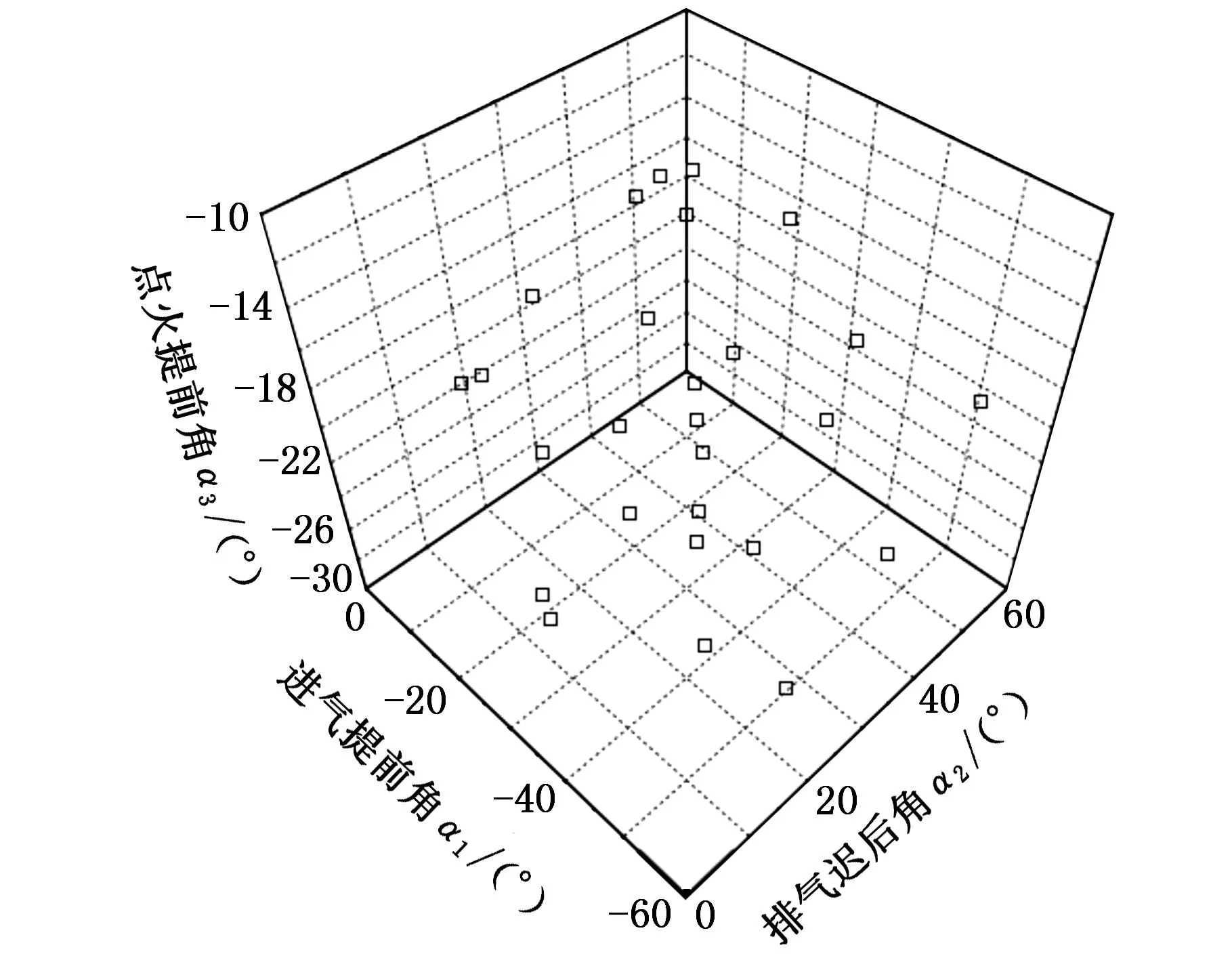
图5　ULH生成的设计变量空间

对以上设计点执行仿真计算，最终得到建立响应曲面所需的初始仿真数据。

3.3响应曲面的建立

由试验设计得到的一组涵盖仿真模型信息的数据点，利用回归分析方法可以建立起所需的响应曲面模型。径向基函数法(radial basis functions, RBF)是一种常用的回归分析方法，可以较好地由ULH得到的数据点建立关于配气正时的响应曲面。RBF适于多个离散变量插值。

图6　有效功率响应曲面的3D曲面

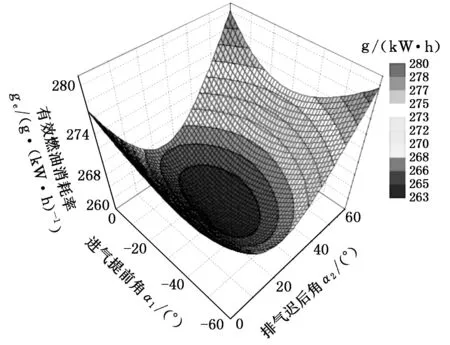
图7　有效燃油消耗率响应曲面的3D曲面

本文有3个设计变量，2个优化目标，可以建立6个能够直观描绘响应曲面的3D曲面。选取其中两个具有代表性的3D曲面，如图6、图7所示。从图中可以看出，在设计变量空间中存在最优解。

3.4检验响应曲面的有效性

拟合精度过低的响应曲面可能会计算出错误的优化方案。为了确定建立的响应曲面是否能准确表示GT-Power仿真模型的特性，从而代替仿真模型进一步完成优化，十分有必要检验由径向基函数法差值拟合的响应曲面的有效性。检验响应曲面有效性最通用的方法是在设计变量空间内随机生成几个测试点，并调用仿真模型进行仿真计算，然后检查在测试点处响应曲面上对应值与仿真值的偏离程度。随机选取的8个随机数据点如表3所示。

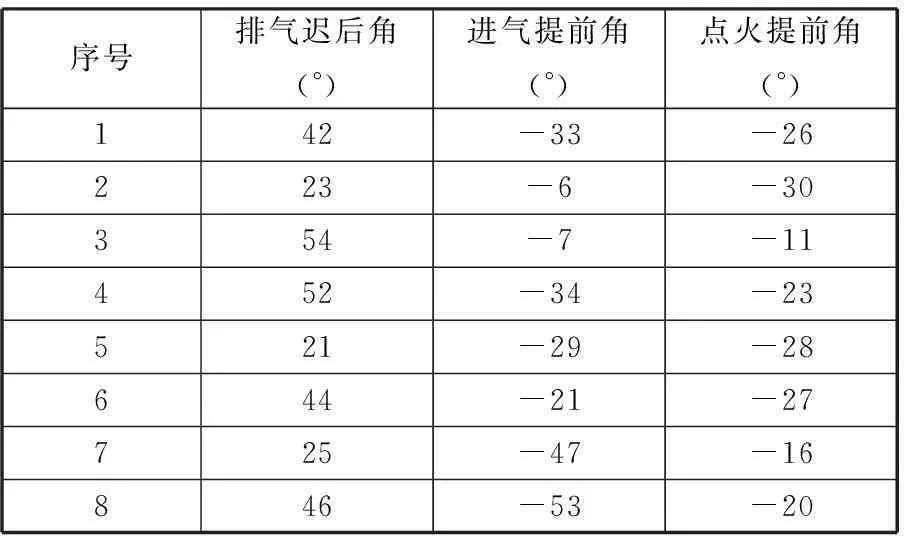
表3　随机生成的8个测试数据点

通过计算相关指数R2值描述响应曲面对仿真模型拟合程度，其计算公式为

(3)

表4　径向基函数拟合响应曲面的R2值

3.5在响应曲面上搜寻最优值

利用验证过的径向基函数法建立的响应曲面，结合优化算法只需要极少的计算时间就可以完成对气门正时的优化。优化参数设置如表2所示。优化算法采用多目标遗传算法(MOGAⅡ)[19]，这是一种采用改进的多元搜寻精英策略的多目标遗传算法，可以避免陷入局部最优而导致早熟收敛。遗传算法初始种群为均匀拉丁超立方法生成的27个设计点，种群代数为100，共对2700个数据点进行了寻优，得到两个优化目标的Pareto前沿如图8所示，该图表示优化算法在响应曲面上搜寻到的所有满足条件的最优解。因为没有设置两个优化目标的权重，所以各个最优解是平等的。将Pareto前沿上的最优解集分析整理后，选取了5个最优解，如表5所示。

图8　优化目标的Pareto前沿

序号进气提前角(°)排气迟后角(°)点火提前角(°)有效功率(kW)有效燃油消耗率(g/(kW·h))1-2831-174.24262.112-2830-174.23258.333-3029-164.23261.934-2928-174.23261.745-3127-164.22261.67

将选取的5个最优解回代到GT-Power进行仿真验证计算，5个最优解全部满足约束条件，由此推断，建立的响应曲面已完全满足优化所需的精度要求，在响应曲面上进行优化得到的最优解是准确可靠的。整个基于仿真的响应曲面气门优化过程，一共调用了27+5+5=37次仿真，其中响应曲面的验证调用了10次仿真，而真正建立响应曲面的过程仅用了27次，即用于试验设计得到初始设计点。如果采用相同的DoE方法和优化算法，但直接进行优化，将对2700个设计点实施仿真，会使得计算量过大。所以响应曲面法在同样完成优化任务的前提下，适当舍弃了过高的精度，从而大幅度提升了优化效率。

4　结论

(1)在不改变原汽油机进排气持续期的情况下，改型的煤油机在常用转速下，相对于原汽油机进气提前角需要推迟10～13°，排气迟后角需要推迟6～10°，同时为了与换气过程相匹配点火提前角要推迟至-17～ -16°，优化后有效功率约提升4%，有效燃油消耗率基本保持不变。

(2)相比于直接优化方法，将发动机仿真模型与响应曲面法结合的方法，在保证必要计算精度的前提下，显著节省仿真计算次数，提高优化设计效率，可以得到准确可靠的优化结果。

[1]杨致明, 李隆强. 汽油机改烧煤油或柴油的研究[C]//中国内燃机学会特种发动机分会四届一次学术交流会论文集.北京，2006：42-50.

[2]潘钟键, 何清华, 杨晶. 活塞航空重油发动机发展现状[J]. 科技导报,2013,31(34):65-68.

Pan Zhongjian,He Qinghua,Yang Jing.Development Status of Piston Aviation Heavy Oil Engine[J].Science & Technology Review,2013,31(34):65-68.

[3]张全逾, 黎苏, 左明伟. 配气相位对天然气发动机性能的影响[J].河北工业大学学报，2013,42(5):50-54.

Zhang Quanyu, Li Su, Zuo Mingwei. Study on Effect of Valve Timing on Performance of CNG Engine[J]. Journal of Hebei University of Technology, 2013,42(5): 50-54.

[4]高进, 肖龙, 任建敏, 等. 141F小型汽油机数值模拟及性能优化[J]. 内燃机,2013(4):30-33.

Gao Jin, Xiao Long, Ren Jianmin, et al. Numerical Simulation and Optimizing of 141F Gasoline Engine[J]. Internal Combustion Engines, 2013(4): 30-33.

[5]肖民, 焦涛. 6L21/31型中速柴油机配气相位及凸轮型线优化[J]. 内燃机与动力装置,2013,30(6):26-31.

Xiao Min, Jiao Tao. Optimization of Valve Timing and Cam Profile of 6L21 /31 Medium Speed Diesel Engine[J]. Internal Combustion Engine & Powerplant, 2013,30(6): 26-31.

[6]李露露, 黄锦成, 梁燕成, 等. 废气涡轮增压汽油机可变配气相位的优化研究[J]. 装备制造技术,2012,28(1):8-10.

Li Lulu, Huang Jincheng, Liang Yancheng, et al. Optimize Study on Variable Valve Timing in Exhaust Turbocharged Gasoline Engine[J]. Equipment Manufacturing Technology, 2012,28(1): 8-10.

[7]黄粉莲, 纪威, 张禄, 等. 基于OPTIMUS的柴油机配气正时及喷油提前角的优化[J]. 农业工程学报,2012,28(15):27-32.

Huang Fenlian, Ji Wei, Zhang Lu, et al. Optimization of Valve Timing and Injection Advance Angle of Diesel Engine Based on OPTIMUS[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012,28(15): 27-32.

[8]张学文, 申立中, 雷基林, 等. 四气门两缸增压柴油机配气相位优化[J]. 昆明理工大学学报(自然科学版),2012,37(1):47-52.

Zhang Xuewen, Shen Lizhong, Lei Jilin, et al. The Valve Timing Optimization of Turbocharged & 4-Valve 2-Cylinder Diesel Engine[J]. Journal of Kunming University of Science and Technology(Natural Science Edition), 2012,37(1): 47-52.

[9]周刊, 杜爱民. 基于GT-POWER DoE的发动机多参数优化[J]. 佳木斯大学学报(自然科学版),2012,30(5):701-705.

Zhou Kan, Du Aimin. Multi-parameter Optimization of Engine Based on GT-POWER DoE[J]. Journal of Jiamusi University(Natural Science Edition), 2012,30(5): 701-705.

[10]叶年业, 刘洁, 倪计民, 等. 车用汽油机流动过程模拟及基于DoE的配气相位优化[J]. 内燃机工程,2011,32(4):72-75.Ye Nianye, Liu Jie, Ni Jimin, et al. Flow Process Modelling of Gasoline Engine and Optimization of Valve Timing Based on DoE[J]. Chinese Internal Combustion Engine Engineering, 2011,32(4): 72-75.[11]Myers R H, Montgomery D C, Ma C C. Response Surface Methodology: Process and Product Optimization Using Designed Experiments[M]. Germany: John Wiley & Sons, 2009.

[12]Shi Yu GH-W, Reitz Rolf Deneys. Computational Optimization of Internal Combustion Engines[M]. London: Springer, 2011.

[13]Santner T J, Williams B J, Notz W I. The Design and Analysis of Computer Experiments[M].New York: Springer, 2003.

[14]Rasmussen C E. Gaussian Processes for Machine Learning[J].International Journal of Neural Systems, 2006,14(6):3011-3015.

[15]Wendland H. Scattered Data Approximation[J]. Cambridge Monographs on Applied & Computational Mathematics, 2010,10(3):336.

[16]Berbecea A. Multi-level Approaches for Optimal System Design in Railway Applications[D]. Wikipedia,France: Université Lille Nord, 2012.

[17]Persson J. Design and Optimization under Uncertainties: A Simulation and Surrogate Model Based Approach[D]. Linkoping, Sweden: Linkoping University, 2012.[18]Mckay M D, Beckman R J, Conover W J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code[J]. Technometrics,2000,42(1):55-61.[19]Poles S. MOGA-Ⅱ. An improved Multi-objective Genetic Algorithm[CP/DK]. Trieste, Italy:Esteco, 2003.

(编辑郭伟)

Optimization of Valve Timing of a Kerosene Engine Based on RSM

Zhang WeiMao JianguoWei TeteHe Xiaoming

Nanjing University of Aeronautics and Astronautics,Nanjing,210016

Using optimization method of response surface based on the simulation, modified kerosene engine valve timing multi-objective optimization problem was studied. A simulation model of the engine performance was established with the intake, exhaust timing, ignition advance angle as optimization variables and with the improvement of brake power and brake special fuel consumption as the design optimization target. The results show that: relative to this gasoline engine, intake valve opening timing of modified kerosene engine must be postponed, the exhaust valve closing time must be postponed, and ignition timing must be advanced for better engine performance; and applications of response surface methodology can improve the efficiency of optimization.

kerosene engine；numerical simulation；respouse surface methodology(RSM)；valve timing

2015-06-13

国家自然科学基金青年基金资助项目(11202096)

U46DOI：10.3969/j.issn.1004-132X.2016.07.014

张伟，男，1990年生。南京航空航天大学能源与动力学院硕士研究生。主要研究方向为活塞发动机仿真与控制。毛建国，男，1957年生。南京航空航天大学能源与动力学院副教授。魏特特，男，1990年生。南京航空航天大学能源与动力学院硕士研究生。何小明，男，1972年生。南京航空航天大学能源与动力学院讲师。