无模型机械臂BP神经网络状态观测及反演跟踪控制

李　光　符　浩

湖南工业大学,株洲,412007



无模型机械臂BP神经网络状态观测及反演跟踪控制

李光符浩

湖南工业大学,株洲,412007

针对摩擦阻尼及模型参数不确定的情况，运用反演控制设计策略，针对多连杆机械臂提出了一种基于神经网络观测器的无模型轨迹跟踪控制方法。运用带有修正项的自适应BP神经网络观测器对不可测状态量进行观测，同时对系统模型进行在线逼近。在此基础上设计了基于观测状态和逼近模型的反演跟踪控制器， Lyapunov稳定性理论证明了该控制器能够保证跟踪误差的有界和闭环系统中所有信号的有界。跟踪给定轨迹的仿真实验证明了该方法的有效性。

机械臂；状态观测器；BP神经网络；反演控制

0　引言

多连杆机械臂系统是一个复杂的多输入多输出非线性系统，具有时变、强耦合和高度非线性的动力学特性。实际工程应用中，系统不可避免地存在大量的干扰与不确定性；同时，考虑成本、硬件安装等因素，全局状态向量可测量也是难以实现的。因此，高鲁棒性的控制器一直是机器人控制领域研究的重点。

文献[1]用一种非线性干扰观测器观测系统的不确定性和干扰，设计了自适应反演滑模控制策略，在全局状态向量可测、干扰为缓变量(即干扰项对时间的导数为0)的条件下，实现机械臂位置跟踪控制。文献[2]提出了一种基于神经网络的自适应输出反馈控制方法，控制器由基于动态补偿器的输出反馈、神经网络自适应和鲁棒三个控制项组成，基于系统的名义模型，可以完成对机械臂端点位置和速度的跟踪控制。文献[3-4]利用机械臂动力学系统中惯性矩阵正定有界(包括其导数及逆同样有界)的特性，分别提出了无模型的机械臂轨迹跟踪控制策略。文献[3]将神经网络作为控制器，利用非线性映射能力来逼近各种未知非线性项，同时通过在控制律中加入鲁棒项来消除逼近误差。文献[4]利用确定学习理论设计了一种新的自适应神经网络控制器，不仅实现了闭环系统所有信号的最终一致有界，而且在稳定的控制过程中保证了部分神经网络权值的收敛以及未知闭环系统动态的局部逼近。以上研究均是基于系统全局状态可测量的条件。

本文运用反演控制设计方法，充分考虑系统不确定性和扰动的实际情况，提出了一种无模型机械臂输出反馈控制设计策略。应用非线性系统观测器的设计方法，首先设计了基于神经网络的输出反馈速度状态观测器，权值自适应律中修正项的引入提高了神经网络的逼近精度和鲁棒性；之后将逼近模型直接运用于反演控制设计过程，为避免反演法中对中间虚拟控制信号进行求导计算而导致的系统方程微分项的膨胀问题,引入了动态面控制技术[5-8]。

1　机械臂动力学模型

在计及连杆转动关节非线性阻尼的情况下，n连杆机械臂动力学行为描述如下[9]：

(1)

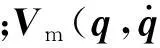
机械臂动力学方程(式(1))具有以下性质：矩阵H(q)的逆矩阵存在,并且H(q)和H-1(q)作为q的函数是一致有界的。

(2)

f(x)=-H-1(x1)[Vm(x1,x2)x2+τ1(x2)+G(x1)]

其中，0∈Rn×n为零矩阵,I∈Rn×n为单位矩阵。

在机械臂的实际工作中，由于负载的变化导致连杆质心和质量的不确定，难以获得准确的连杆惯性矩阵。同时，连杆转动关节处的摩擦因数未知。因此,以上非线性函数向量f(·),g(·)是不确定的，在本文中假设完全未知。

2　基于神经网络观测器的反演控制策略

2.1状态观测器设计

定义

F(x,τ)=f(x)+g(x)τ-τ

(3)

原系统的状态空间表达式(式(2))可改写为

(4)

分析动态系统(式(4))可知，矩阵对(A,C)为可观测对。以BP神经网络对未知非线性函数F(x,τ)进行逼近，设计以下神经网络状态观测器：

(5)

根据前馈神经网络具有任意精度的逼近性能，对非线性项的逼近可以获得相对较为理想的结果。在给定逼近误差ε(·)>0的情况下，一定存在权值和阈值构成的三层BP神经网络在误差允许的范围内逼近非线性函数[10]，即

(6)

(7)

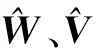
(8)

参照文献[11]选择如下权值更新律：

(9)

其中，η1,η2为学习率，η1,η2>0；ρ1、ρ2为修正率，取小的正常数。

由式(4)～式(8)可得状态观测误差方程：

(10)

其中,ξ(t)为有界误差项，即‖ξ(t)‖≤ξN。权值更新律(式(9))可以改写为以下形式：

(11)

为对所设计的观测器进行稳定性分析，构造以下Lyapunov函数：

(12)

其中，P为正定对称矩阵，并满足以下方程：

(13)

其中,Q为正定对称矩阵。

将式(12)对时间求导，得

(14)

将式(10)、式(11)和式(13)代入式(14)，得

(15)

根据矩阵秩的定义和性质，有以下等式和不等式成立：

(16)

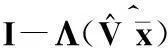
(17)

因此有

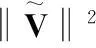
(18)

l1=‖PB‖ξN

l3=ρ1‖C‖l4=mη2‖CTCA0-1B‖

l6=ρ2‖C‖

其中，λmin(Q)为矩阵Q的最小特征值， li(i=1,2,…,6)均为大于0的常数。

式(18)进一步可写为

(19)

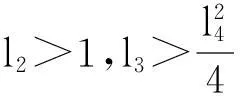
进一步分析权值更新律式(11)，其中第一式可改写为

(20)

同理权值更新律(式(11))中第二式可改写成

(21)

2.2反演控制器的设计

改写观测器式(5)第一式：

(22)

(23)

对时间求导得

(24)

利用式(22)第一式,有

(25)

(26)

(27)

式中,k1∈Rn×n为正定对角常数矩阵。

(28)

其中，β2∈Rn×n为滤波器的时间常数对角矩阵，且其对角元素均大于0。

因此，式(26)可改写为

(29)

定义滤波误差为

(30)

于是,其滤波误差微分为

(31)

将式(27)、式(29)、式(30)代入式(24)，可得

(32)

定义Lyapunov函数：

(33)

对其求导并应用式(32)得

(34)

对式(26)求导，并利用式(22)第二式，得

(35)

定义Lyapunov函数：

(36)

将上式对时间求导，得

(37)

于是，设计控制律为

(38)

其中，k2∈Rn×n为正定常数矩阵。因此，式(37)可写成

(39)

(40)

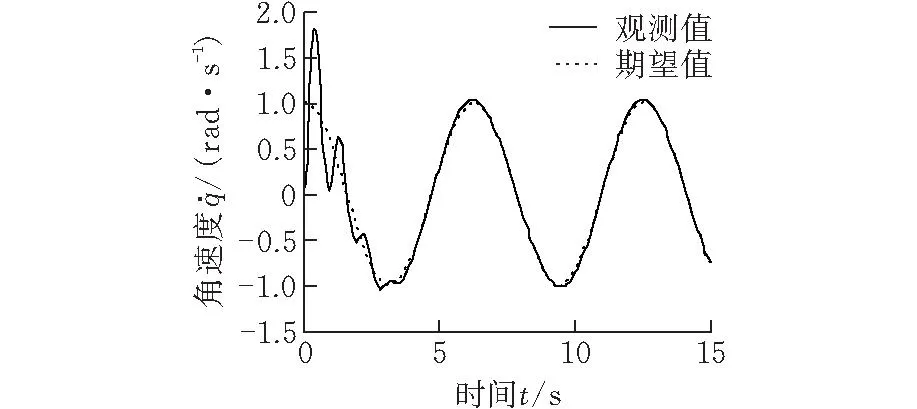
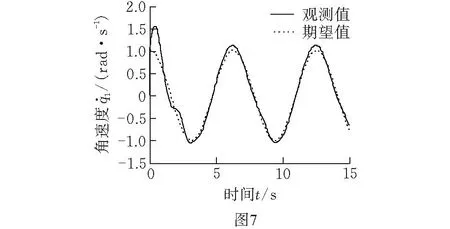
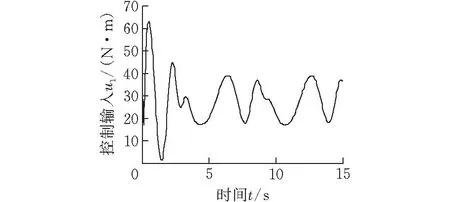
0<ϖ

因此，有结论Ⅱ：对于多连杆机械臂系统(式(2))，其状态变量由观测器(式(8))获得，应用控制输入(式(38))，则：① 状态观测值的跟踪误差有界，且收敛到原点的一个小邻域内；② 结合结论Ⅰ，系统的实际跟踪误差e=y-yd收敛于可调的小邻域上。

最终控制系统框图如图1所示。

图1　控制系统框图

3　仿真分析

为验证提出的控制策略的有效性，分别以单连杆和二连杆机械臂系统为对象来进行仿真研究。

3.1单连杆机械臂

构建观测器中的三层BP神经网络，其中隐含层节点取10，权值更新律(式(9))中的学习率和修正率分别为η=13 000 ，ρ=5。设计极点配置矩阵L，使得Hurwitz矩阵A0=A-LC的极点为P0=[-10+10i-10-10i]，正定矩阵Q=diag(50)。

反演控制器参数设置如下： k1=k2=50，β2=0.8，杆转角跟踪连续信号yd=sint。

3.2二连杆机械臂

对应动态方程式(1)中各矩阵、向量为

H(q)=

G(q)=

构建观测器中的三层BP神经网络，其中隐含层节点取20，权值更新律(式(9))中的学习率和修正率分别为η1=η2=100 000,ρ1=ρ2=5。设计极点配置矩阵L，使得Hurwitz矩阵A0=A-LC的极点为P0=[-15+14i-15-14i-13+15i-13-15i]，正定矩阵Q=diag(50)。

反演控制器参数设置如下：k1=k2=diag(50)，β2=diag(0.8)，杆转角跟踪连续信号yd=[sintcost-0.5]T。

单连杆系统仿真结果如图2～图4所示。从图2可以看出，机械臂转角能够跟踪期望的连续轨迹，角位移跟踪误差一致收敛于一个小的误差，约为0.1%；图3所示为对转角关节速度的状态估计，所设计的观测器能快速准确地估计出系统不可测量的状态向量；图4所示为有界的关节控制输入。

图2　单连杆系统关节轨迹跟踪

图3　单连杆系统关节速度观测值与期望值

图4　单连杆系统关节控制输入

二连杆系统仿真结果如图5～图10所示。从图5、图6可以看出，角位移跟踪误差一致收敛于一个小的误差，约为2%；图7、图8所示为对转角关节速度的状态估计，所设计的观测器能快速准确地估计出系统不可测量的状态向量；图9、图10所示为有界的关节控制输入。

图5　二连杆系统关节1轨迹跟踪

图6　二连杆系统关节2轨迹跟踪

图7　二连杆系统关节1速度观测值与期望值

图8　二连杆系统关节2速度观测值与期望值

图9　二连杆系统关节1控制输入

结合图2～图10,对比单连杆和二连杆的控制仿真结果，可以看到随着系统复杂度增加(机械臂自由度的增加)，调节BP神经网络的设计参数，可以保证对不可测状态的观测精度和动力学系统的在线逼近，并达到良好的轨迹跟踪控制效果，同时观测和控制的过渡时间并没有明显增加。

4　结语

针对参数完全未知并存在外界干扰的多连杆机械臂系统，提出了一种基于BP神经网络状态观测器的反演控制方案，观测器和控制器的设计均不依赖系统的模型参数，融合了状态观测、非线性系统逼近和轨迹跟踪控制，具有较高的控制鲁棒性。分别以单连杆和二连杆机械臂为例进行了控制仿真分析，结果表明神经网络观测器能快速准确地对系统不可测速度向量进行在线观测，同时完成对系统的逼近，基于观测状态量和逼近系统设计的反演控制器能够实现对期望轨迹良好的跟踪。

[1]席雷平，陈自力，齐晓慧.基于非线性干扰观测器的机器臂自适应反演滑模控制[J].信息与控制,2013,42(4):470-477.

Xi Leiping,Chen Zili,Qi Xiaohui.Adaptive Backstepping Sliding Mode Control for Robotic Manipulator with Nonlinear Disturbance Observer[J].Information and Control，2013,42(4):470-477.

[2]贾鹤鸣,宋文龙,郭少彬,等.基于神经网络的机械臂自适应输出反馈控制设计[J].应用科学学报,2013,31(4):427-433.

Jia Heming,Song Wenlong,Guo Shaobin,et al.Adaptive Output Feedback Control of Manipulators Based on Neural Network[J].Jounal of Applied Sciences,2013,31(4): 427-433.

[3]付涛,王大镇,弓清忠,等.改进神经网络自适应滑模控制的机器人轨迹跟踪控制[J].大连理工大学学报,2015,54(5):523-530.

Fu Tao,Wang Dazhen,Gong Qingzhong,et al.Robitic Trajectory Tracking Control of Improved Neural Network Adaptive Sliding Mode Control[J].Journal of Dalian University of Technology,2015,54(5):523-530.

[4]吴玉香，张景，王聪.机械臂的自适应神经网络控制与学习[J].机械工程学报,2013,49(15):42-48.

Wu Yuxiang,Zhang Jing,Wang Cong.Adaptive Neural Network Control and Learning for Robot Manipulator[J].Journal of Mechanical Engineering,2013,49(15):42-48.

[5]陈伟,卢京潮,袁燎原,等.基于高增益观测器的航迹角自适应反步控制[J].北京航空航天大学学报，2013,19(9):1414-1420.

Chen Wei, Lu Jingchao, Yuan Liaoyuan, et al. Adaptive Backstepping Control for Flight Path Angle Based on High Gain Observer[J].Journal of Beijing University of Aeronautics and Astronautics, 2013,19(9):1414-1420.

[6]陈洁,周绍磊,宋召青.高超声速飞行器迎角观测器及控制器设计[J].北京航空航天大学学报,2011,37(7):827-832.

Chen Jie,Zhou Shaolei,Song Zhaoqing.Nonlinear Modelling and Open-loop Dynamatics Characteristics for One Hypersonic Aircraft[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(7):827-832.

[7]李红春.基于动态面技术的自适应神经网络控制研究[D].扬州:扬州大学,2007.

[8]Yoo S J， Park J B， Choi Y H.Output Feedback Dynamic Surface Control of Flexible-joint Robots[J].International Journal of Control Automation and System,2008,6(2):223-233.

[9]蔡自兴.机器人学[M].2版.北京：清华大学出版社，2009.

[10]徐志超，周玉国，于凤满.基于改进神经网络的非线性系统观测器设计[J].微型机与应用,2011,30(8):76-78.

Xu Zhichao,Zhou Yuguo,Yu Fengman.Design of Observer for Nonlinear Systems Based on Improved Neural-network[J].Technique and Method,2011,30(8):76-78.

[11]Abdollahi F,Talebi H A,Patel R V.A Stable Neural Network-based Observer with Application to Flexible-joint Manipulators[J].IEEE Transactions on Neural Networks,2006,17(1):118-129.

(编辑陈勇)

BP Neural Network State Observation and Backstepping Tracking Control of Model-free Robotic Manipulators

Li GuangFu Hao

Hunan University of Technology,Zhuzhou,Hunan,412007

A model-free trajectory tracking control algorithm was proposed for multi-link robotic manipulators with friction damping and model parameter uncertainties based on the backsteeping techniques. An adaptive BP neural network state observer with modification items was used to obtain the unmeasured states and approximated the system model online.Then,a backstepping tracking controller was developed, which took advantages of the observed state values and dynamics.Based on Lyapunov stability theory it is proved that presented controller can guarantee the tracking accuracy and all signals involved are bounded. Finally, it demonstrates that the strategy is effective by the simulation of tracking expected trajectory.

robotic manipulator; state observer; BP neural network; backstepping control

2015-05-14

国家自然科学基金资助项目(61273157)

TP241.3DOI：10.3969/j.issn.1004-132X.2016.07.002

李光,男，1963年生。湖南工业大学机械工程学院教授、博士。主要研究方向为复杂机电一体化系统建模和控制。符浩(通信作者),男,1988年生。湖南工业大学机械工程学院硕士研究生。