气缸冲击动力学建模与仿真分析

杜群贵　孙智权　黄崇溪　翟晓晨

华南理工大学,广州,510640



气缸冲击动力学建模与仿真分析

杜群贵孙智权黄崇溪翟晓晨

华南理工大学,广州,510640

将气缸在行程末端的冲击问题看成一个由细长活塞杆、质量负载、活塞以及端盖组成的振动系统。首先应用弹性体的一维波动方程建立细长活塞杆纵向振动变形的数学模型，用模态叠加方法解析了冲击力、接触位移以及接触时间。然后利用非线性有限元软件LS-DYNA对气缸冲击过程进行数值仿真计算分析，详细研究了当驱动负载质量以及活塞初始冲击速度不同时，活塞冲击接触面接触合力和接触作用时间的变化情况。对比分析了理论解析解与LS-DYNA数值解，验证了解析解的准确性，得出了冲击力分别随速度和负载的变化规律；进一步对冲击振动响应进行了频率分析，并研究了气缸冲击力的变化原因。研究结果为气缸的设计和使用提供了理论和实际参考。

气缸冲击力；解析解；LS-DYNA仿真；频率分析

0　引言

随着气动技术的飞速发展，气缸广泛地应用于各种工业生产线上。但是，由于气动系统中介质空气的高度可压缩性和低黏度等内在固有特性，当活塞运行到行程末端时就会产生冲击端盖现象。同时，气缸也不可避免地会由于安装制造误差、供气压力波动、缓冲不良、负载惯性以及运行一段时间之后紧固螺栓松动等外在因素，产生活塞冲击端盖现象[1]，并伴随着不良振动与噪声，这也是导致气缸失效的最主要原因。

气缸的冲击问题是一个经典的杆结构弹性碰撞力学问题。近年来，国内外学者针对杆的弹性碰撞问题作了很多研究。文献[2]采用波传播法给出了质点和均匀杆纵向碰撞响应解析解；文献[3-4]也采用波传播法解析了一般边界条件下杆的纵向冲击振动问题 ，但解析式随着波传播次数的增加而变得过于复杂，其工程应用难以推广。文献[5-6]采用模态分析方法解析了杆的点弹性碰撞问题，但局限于特殊的边界条件；文献[7-8]采用直接模态叠加法将碰撞问题转化为具有初速度的振动问题，解析了不同边界条件、多种截面形状的杆类冲击问题的频率方程及动力响应。但是，对于类似气缸存在复杂边界和初始条件下的冲击破坏现象的建模研究甚少，对其冲击力大小的预估大都基于经验。

基于以上原因，本文在不考虑缓冲垫和气缓冲的情况下对气缸冲击现象进行简化建模研究，求解出冲击力的解析式，并与有限元仿真数值解进行了对比，从而验证解析式的可靠性，此外，还分析了冲击力波动变化的规律及原因。

1　气缸碰撞系统建模与解析

本文所研究的标准型单杆双作用气缸结构简图如图1所示。

1.质量负载　2.活塞杆　3.端盖　4.活塞　5.缸筒图 1　气缸结构简图

该气缸缸筒与无杆侧端盖压成一体，缸筒与有杆端盖3处的连接为螺纹连接，轴向尺寸短，质量比其他系列气缸小10%～15%。气缸最大工作压力为1.0 MPa,活塞工作速度为50～1000 mm/s，主要运用于装配生产线上轻型物料输送。

笔者在该气缸可靠性试验研究的过程中发现气缸工作一段时间之后，会出现端盖与缸筒螺纹连接松脱失效以及气缸安装紧固螺栓松动的现象。这是由于行程末端活塞对端盖的长期冲击造成的，故对此冲击现象进行建模研究。

对气缸碰撞系统数学建模时，为了便于简化分析，将质量负载看成细长活塞杆左端部的一个集中质量，将活塞看成活塞杆右端部的一个集中质量，集中质量随杆端横截面一起振动。将端盖与活塞的碰撞接触部分看成一个等效接触弹簧，活塞、活塞杆和负载以一定的初速度冲击接触弹簧，弹簧压力等效为气缸冲击力[9]。并认为冲击过程中杆的横截面始终保持为平面，且界面上的应力分布均匀，忽略各部分重力的影响。其碰撞系统简化模型如图2所示。

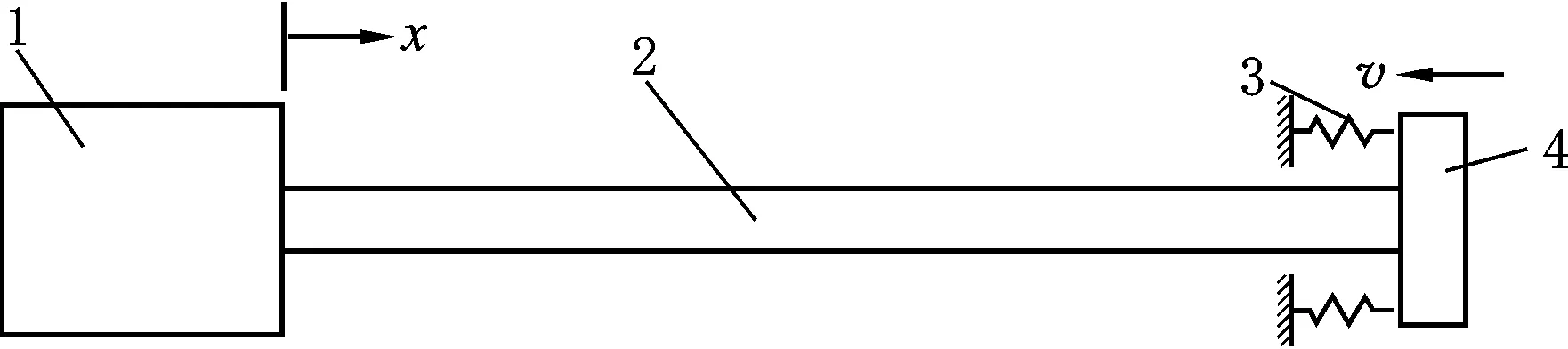
1.质量负载　2.活塞杆　3.等效接触弹簧　4.活塞图 2　碰撞系统简化模型

1.1碰撞系统数学模型的建立

图2中活塞杆长为l，横截面积为A，质量密度为ρ，弹性模量为E，等效接触弹簧刚度系数为k，负载质量为M，活塞质量为m，将质量负载位置处杆端作为坐标原点，分别建立杆的纵向碰撞问题的控制方程、边界条件和初始条件[10]。

杆的自由振动方程:

(1)

式中，u为杆的纵向振动位移；x为杆的某一横截面距离坐标原点的位移；t为振动时间。

碰撞过程中边界条件:

(2)

(3)

初始条件:

u(x,0)=0

(4)

(5)

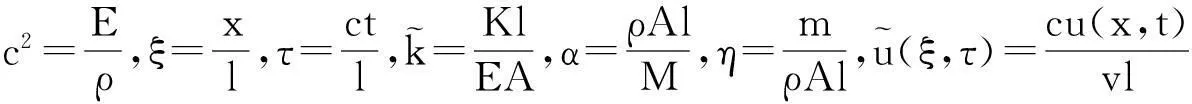
(6)

边界条件转化为

(7)

(8)

初始条件转化为

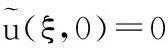
(9)

(10)

1.2碰撞模型的求解

(11)

(12)

(13)

(14)

其中，λ为无因次频率，由式(11)得到主振型通解为

U(ξ)=acosλξ+bsinλξ

(15)

式中，a、b分别为主振型中余弦、正弦信号的幅值。

将式(15)代入式(13)、式(14)得

(16)

由式(16)得到频率方程：

(17)

由式(15)、式(17)得到各阶主振型函数：

(18)

由式(12)解得各阶时间函数：

Ti(τ)=Cicosλiτ+Disinλiτ

(19)

式中，Ci、Di分别为第i阶时间函数中余弦信号和正弦信号的幅值。

根据模态叠加法，杆的振动位移为无穷个主振动的叠加：

(20)

1.3主振型的正交性求解

为了求得各阶时间函数中系数Ci、Di，首先应求得主振型之间的正交性。设Ui(ξ)、Uj(ξ)分别是对应于无因次频率λi及λj的主振型，由式(11)有

(21)

(22)

对式(21)等号两边同时乘以Uj(ξ)并对其从0到1求积分，得

(23)

利用分部积分法可将式(23)等号左边写为

(24)

联立式(23)、式(24)并化简，得

(25)

同理，对式(23)化简得

(26)

(27)

为了便于连续性求解，引入δ函数，得到主振型的正交性关系式：

(28)

(29)

1.4冲击接触求解

由初始条件可得

(30)

(31)

利用主振型的正交性，将式(30)、式(31)等号两边同时乘以[α+δ(ξ)+αηδ(ξ-1)]Ui(ξ)，然后从0到1区间求定积分，可以求解得到:

Ci=0

(32)

(33)

则杆的振动位移解析式为

(34)

在活塞冲击端盖处，有x=l，将其代入式(34)，可得到冲击处杆端横截面振动位移：

(35)

用等效接触弹簧所受的压力大小来表征碰撞过程中冲击力大小，得到冲击力表达式：

(36)

2　基于LS-DYNA的有限元仿真分析

以图1所示的典型气缸结构为基础，忽略结构中倒角、圆角、气孔等因素，根据该气缸实际结构尺寸，建立简化的有限元仿真模型。由于气缸为轴对称性结构，利用其对称性可以简化模拟过程和减少自由度，并缩短分析所需计算时间。本文所采用的1/2模型如图3所示。

图 3　气缸活塞冲击端盖有限元模型

活塞和活塞杆的材料为结构钢，端盖和缸筒的材料为铝合金，有限元仿真时均采用线弹性材料模型。其材料性能参数见表1。

表 1　材料性能参数

气缸装配体模型均采用sweep扫掠方式划分网格，网格均为八节点六面体单元。将缸筒与端盖、活塞与活塞杆以及质量负载与活塞杆的连接设置成固连绑定接触，活塞杆与端盖导向环的相对滑动以及活塞与端盖的碰撞接触采用自动面面双向接触(ASTS)。将缸筒右端面和端盖左端面设置成固定约束，将对称面设置成对称约束，保证活动部件可在对称平面内平动。活塞杆与导向环、活塞与端盖的摩擦因数均为0.1。在不考虑重力作用下，给活塞、活塞杆以及质量负载一定的初速度去冲击端盖，仿真得到碰撞冲击响应。

为了有效地处理气缸冲击过程中的接触问题、非线性问题和随时间变化很快的冲击力学过程，LS-DYNA求解器采用显式直接积分方法，采用罚函数法处理冲击过程中的动态接触，并指定输出RCFORC界面合力ASCII文件，获得冲击力的时间历程曲线[11]。

气缸在实际工作过程中，因应用场合不同，气缸搭载的负载和运行速度就不一样，运行到行程末端时，必然产生不同的冲击情况。本文分析了气缸在不同速度和不同质量下的冲击状况，得到了冲击力响应曲线。

3　结果分析

本文研究的典型气缸活塞杆直径d=12 mm，活塞杆长l=193 mm，气缸内直径D=32 mm，端盖长度l1=29 mm，活塞宽度l2=17 mm，活塞质量m=0.08 kg，仿真质量负载长度l3=50 mm，活塞与活塞杆质量比η=0.5，工作行程s=100 mm。

气缸的碰撞为活塞与端盖的短暂接触，由于活塞长度较端盖短，而其弹性模量比端盖大得多，使得活塞的抗压刚度比端盖的抗压刚度大得多，物理建模时将活塞看成一个集中质量，而将端盖看成接触弹簧；此外，由于活塞运行到行程末端时，有杆腔内气体迅速排空，故忽略气体对接触刚度的耦合影响，其等效接触刚度为

1.12×109(N/m)

其中，E1为端盖材料弹性模量，Acon为活塞与端盖碰撞有效接触面积，碰撞处端盖内半径r=10.3 mm。

将上述参数代入解析解中，利用MATLAB编程计算，取前100阶(已趋于稳定)模态叠加，得到理论解析曲线。

3.1冲击力与速度的关系

为了验证解析解表达式中冲击力与冲击速度的线性关系，在负载为20 N的情况下，分别取活塞冲击速度为0.1 m/s、0.2 m/s、0.3 m/s、0.4 m/s、0.5 m/s进行有限元仿真计算，得到在不同速度下的冲击力-时间曲线，如图4所示。并将0.5 m/s冲击速度下的仿真曲线与理论曲线进行对比，如图5所示。

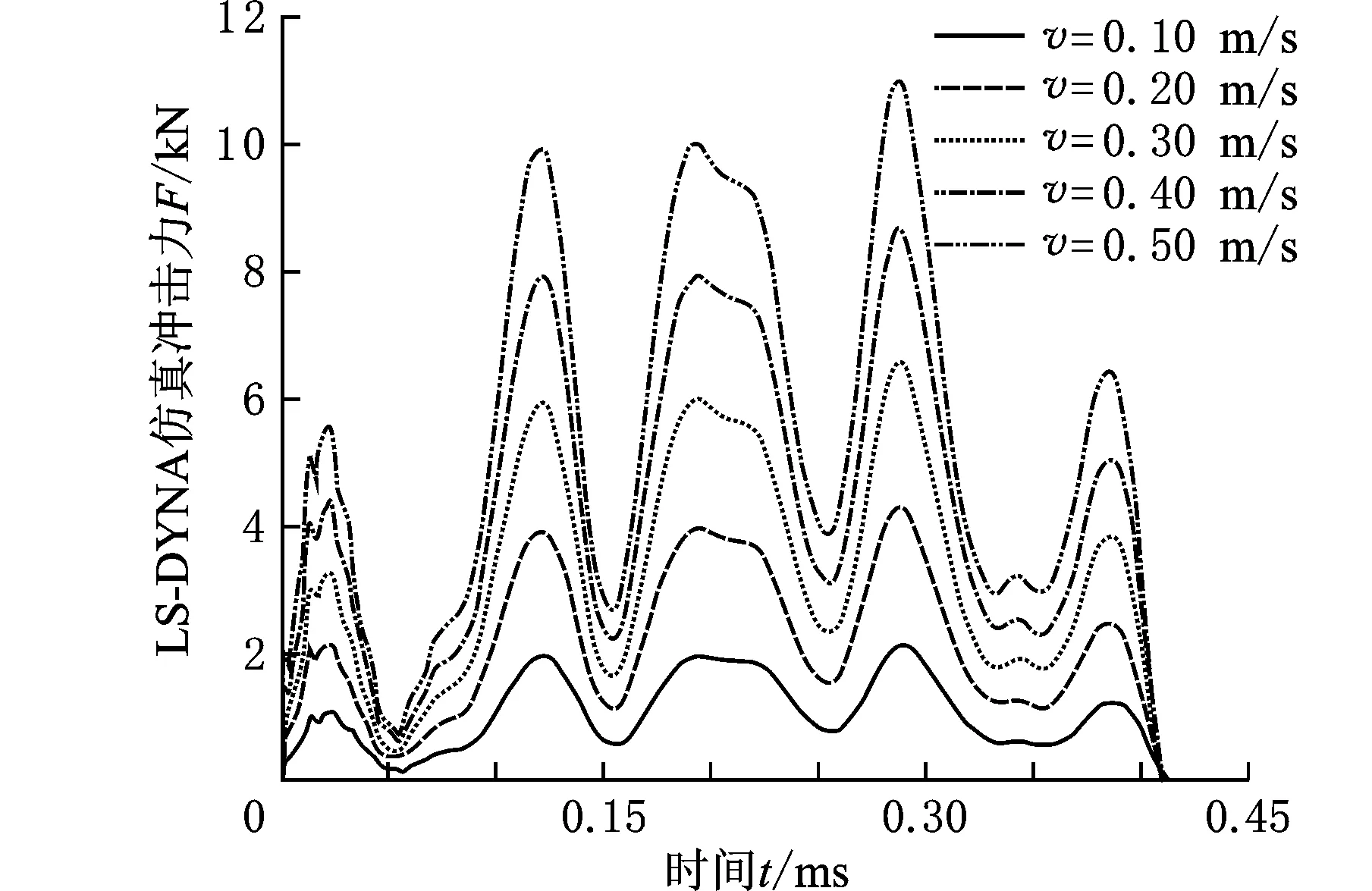
图 4　不同速度下的冲击力-时间曲线

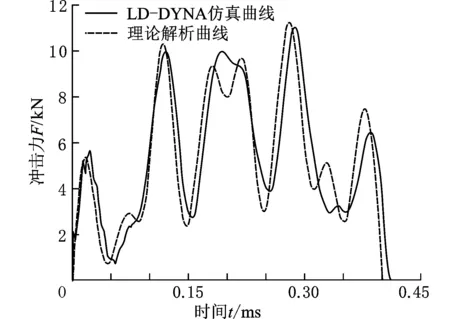
图 5　仿真曲线与理论曲线对比(负载为20 N，冲击速度为0.5 m/s)

从图4可看出，在不同冲击速度下，有限元仿真得到的冲击力波形随时间同步变化，且冲击力随速度线性增大；同时，还可以看出，在同一负载下，冲击作用时间并不随着冲击速度的变化而变化，而是保持不变。从图5可看出，同一冲击条件下，LS-DYNA仿真曲线与理论解析曲线十分吻合，表明仿真结果与解析表达式一致，从而验证了解析表达式中冲击力与速度的关系。

3.2冲击力与负载的关系

通过改变程序中质量比α的大小，得到一系列不同负载下的冲击力响应曲线。同时，为了进一步研究活塞冲击端盖的冲击情况，利用LS-DYNA仿真分析了负载分别为10 N、20 N(图5)、30 N、40 N、50 N在冲击速度为0.5 m/s时的冲击过程，经过后处理得到冲击力-时间历程曲线。将相应的理论解析曲线与LS-DYNA仿真曲线进行对比分析，结果对比如图6～图9所示。

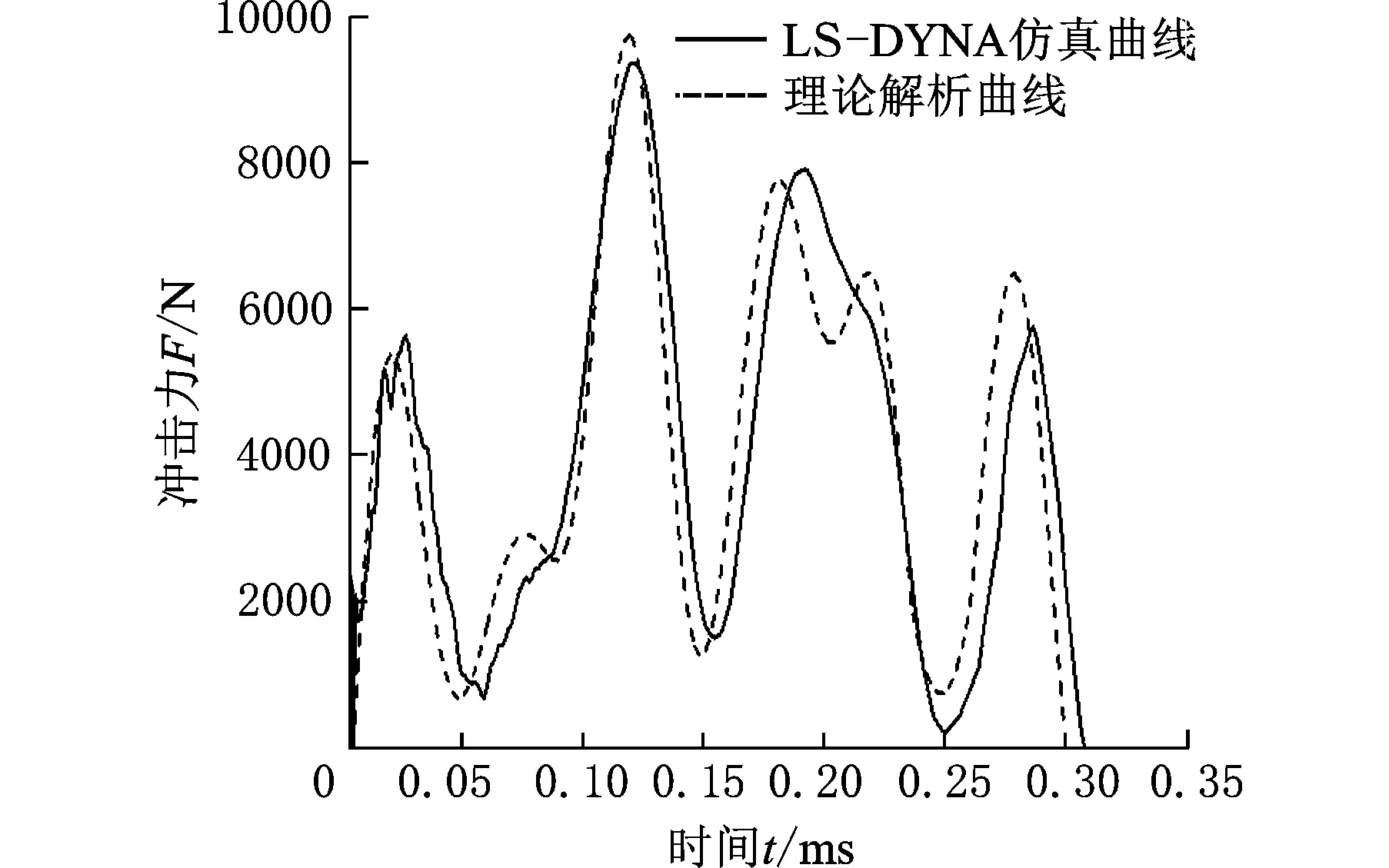
图 6　仿真曲线与理论曲线对比(负载为10 N，冲击速度为0.5 m/s)

图 7　仿真曲线与理论曲线对比(负载为30 N，冲击速度为0.5 m/s)

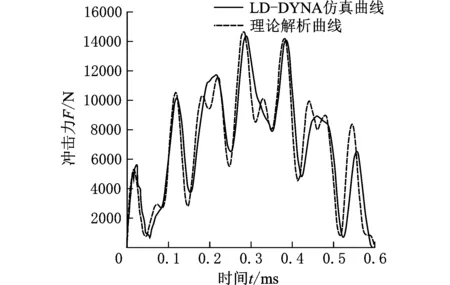
图 8　仿真曲线与理论曲线对比(负载为40 N，冲击速度为0.5 m/s)

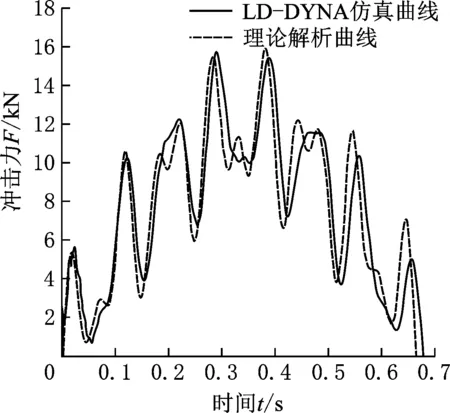
图 9　仿真曲线与理论曲线对比(负载为50 N，冲击速度为0.5 m/s)

结合图5～图9，对比LS-DYNA仿真数值解与理论解析解可知，两者得出的活塞冲击面冲击力时间历程曲线在变化趋势、峰值大小、峰值数量以及冲击作用时间等方面，理论解析与有限元仿真十分吻合，进一步说明了上述物理模型建立以及模型简化处理的正确性和可靠性。

同时，从图6～图9可以看出，冲击力随时间的变化曲线并不具有单峰值和完全对称性，也并不是先增大后减小，而是表现为多峰值且与时间不对称的波动形式。随着负载质量的不断增加，峰值和峰值个数也不断增加，冲击力曲线波动越来越“剧烈”，冲击作用时间也不断变长，这是由于振动频率的变化所致。

3.3振动频率分析

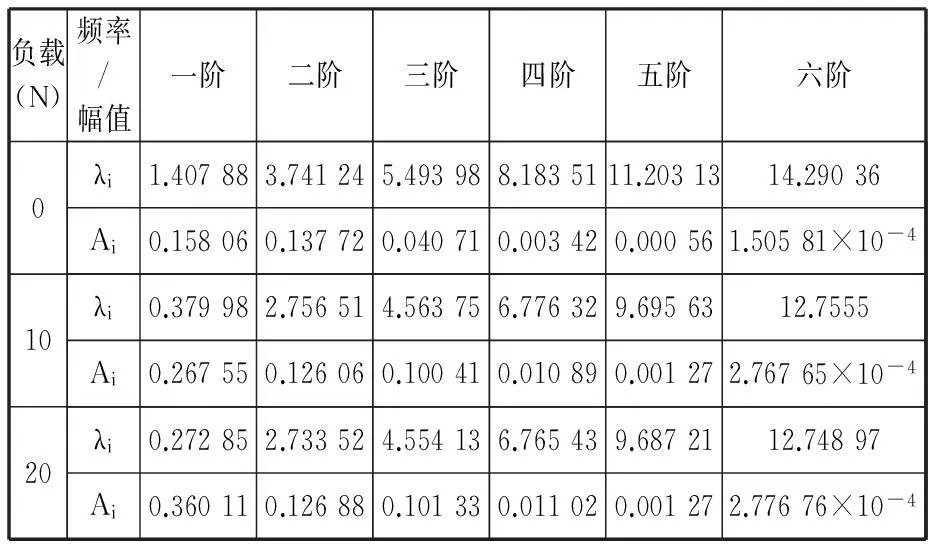
冲击接触面的振动为细长活塞杆各阶主振动在杆碰撞端x=l处的叠加，其振动位移响应是由具有各阶固有频率的谐波信号组成的。不同负载质量下的前6阶无因次固有频率及相应的振幅见表2。

表2不同负载下冲击处振动位移中前六阶振动频率与幅值

负载(N)频率/幅值一阶二阶三阶四阶五阶六阶0λi1.407883.741245.493988.1835111.2031314.29036Ai0.158060.137720.040710.003420.000561.50581×10-410λi0.379982.756514.563756.776329.6956312.7555Ai0.267550.126060.100410.010890.001272.76765×10-420λi0.272852.733524.554136.765439.6872112.74897Ai0.360110.126880.101330.011020.001272.77676×10-4

从表2可以看出，随着频率阶次的增加，其对应的幅值不断衰减，且从第四阶频率开始，衰减得很快。同时，随着负载质量的不断增加，同一阶次的频率值有所减小，但同一阶次的幅值有所增大，且第一阶频率和幅值对负载质量的变化最敏感。但是，随着阶数的增加，各阶频率值和幅值对负载质量的变化越来越不敏感，使得不同负载质量下的各阶频率值和幅值都十分接近。

负载质量的增加，使得振动位移响应中低频(尤其是第一阶频率)成分所占比重不断增加，从而导致冲击力幅值的不断增大；各阶频率的减小，使得冲击作用时间不断增大，冲击力波动变化越来越“剧烈”。

在气缸短暂剧烈的冲击过程中，高频响应衰减得十分迅速。为了使解析式进一步推广到实际运用，在不增大负载质量的情况下，通过取前5阶模态和前100阶模态所得到的冲击力解析曲线与LS-DYNA仿真曲线对比分析，如图10所示。

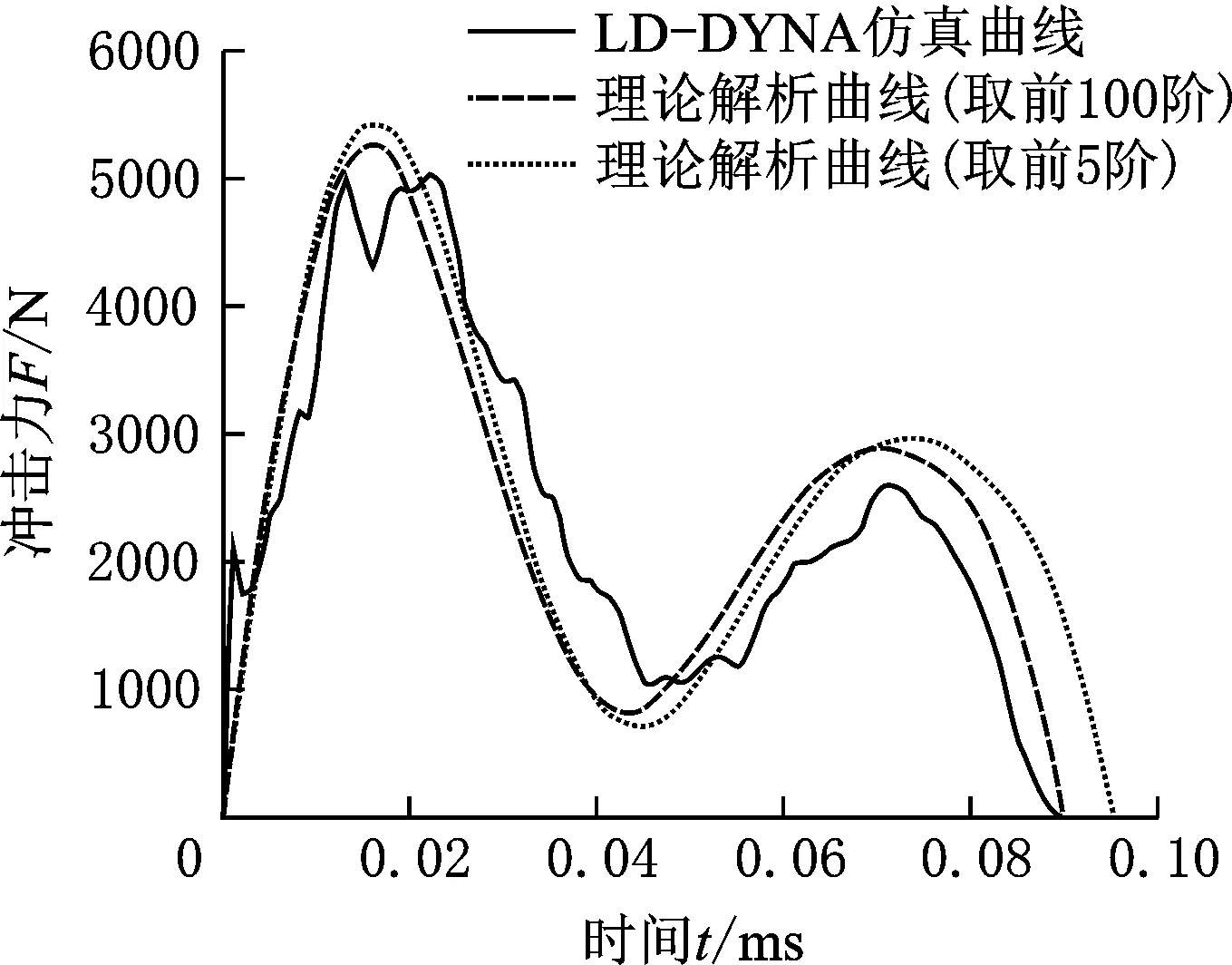
图10　仿真曲线与理论曲线对比(负载为0,冲击速度为0.5 m/s)

图10结果显示,三条曲线十分吻合；同时,模态阶数的减少,使得冲击力幅值和冲击作用时间稍有延长。但随着负载质量的增加，两种阶次取值所得到的冲击力响应曲线趋于重合，差距完全可以忽略不计。这是由于随着负载质量的增加，高频成分衰减得越来越迅速，高阶振型中基本不引起振动。因此，实际工程运用(如螺纹连接设计所考虑的最大冲击力、端盖螺纹孔的大小和深度以及安装方式)中，只需要考虑前面几阶振型分析就足够准确了。

4　结论

(1)本文对气缸行程末端活塞冲击端盖的现象进行动力学建模，将其看成一个振动系统，采用模态分析方法推导出冲击力响应解析解，计算结果与LS-DYNA仿真分析结果吻合，证明了本文简化建模及其解析解的正确性。

(2)冲击力与活塞冲击速度成线性关系；随着负载质量的增加，冲击力幅值不断增大，且波动得更“剧烈”。冲击作用时间随负载质量的增加而变长，但与与冲击速度无关。

(4)冲击响应中第一阶模态对负载变化最敏感，但随着阶次的增加，高阶模态对负载变化越来越不敏感；同时，高阶频率成分衰减得很快，实际运用中只需要取几阶低频分析即可。

(5)研究结果为气缸的可靠性研究提供了理论依据，为气缸的结构(尤其是缓冲结构)设计、活塞螺纹连接、使用安装、维护保养提供了理论依据和数据支持。

[1]廖理.冲击负载下气缸性能测试平台的研究与实现[D].成都:电子科技大学,2013.

[2]Love A E H. A Treatise on the Mathematical Theory of Elasticity [M].New York: Dover, 1994.

[3]张继业,曾京,舒仲周.杆的纵向冲击振动[J].振动与冲击, 1999,18(3):58-63.

Zhang Jiye,Zeng Jing,Shu Zhongzhou.Longitudinal Vibration of Prismatic Bar during Impact[J].Journal of Vibration and Shock,1999,18(3):58-63.

[4]Gan Chunbiao, Wei Yimin, Yang Shixi. Longitudinal Wave Propagation in a Rod with Variable Cross-section[J]. Journal of Sound and Vibration, 2014,333(2) :434-445.

[5]诸德超,邢誉峰. 点弹性碰撞问题之解析解[J].力学学报, 1996,28(1):99-103.

Zhu Dechao, Xing Yufeng. Analytical Solution of Point Elastic Impact between Structures[J].Chinese Journal of Theoretical and Applied Mechanics,1996, 28(1):99-103.

[6]吴家强,王宏志. 杆的纵向冲击问题全过程分析[J]. 振动与冲击,2004,23(1):103-106.

Wu Jiaqiang, Wang Hongzhi. General Procedure for Analysis of Axial Response of Prismatic Bar during Impact[J].Journal of Vibration and Shock, 2004, 23(1):103-106.

[7]鲍四元. 弹性碰撞问题的模态叠加法及哈密顿体系下的计算研究[D].西安:西北工业大学,2005.

[8]Li Q S,Wu J R, Xu J. Longitudinal Vibration of Multi-step Non-uniform Structures with Lumped Masses and Spring Supports[J]. Applied Acoustics,2002,63(3):333-350.

[9]孙龙.潜孔锤及声波钻柔体振动冲击的理论与建模[D].北京:中国地质大学,2014.

[10]倪振华.振动力学[M].西安:西安交通大学出版社,1990.

[11]王泽鹏,胡仁喜,康士廷,等.ANSYS14.5/LS-DYNA非线性有限元分析实例指导教程[M].北京:机械工业出版社,2013.

(编辑陈勇)

Impact Dynamics Modeling and Simulation Analyses of Pneumatic Cylinders

Du QunguiSun ZhiquanHuang ChongxiZhai Xiaochen

South China University of Technology,Guangzhou,510640

Impact of pneumatic cylinder at the stroke terminal was considered to be an integrated system of vibrations, including slender piston rod, mass load, piston and end cover.Based on one-dimensional wave equation, a mathematical model of longitudinal vibration of slender piston rod was established firstly. Impact force,contact displacement and contact time were analyzed by means of mode superposition method.Then impact process of pneumatic cylinder was numerically simulated by nonlinear FEM software LS-DYNA.The variation of impact interface force and contact time were studied in detail under different masses of driven load and impact velocities. Compared with numerical solution of LS-DYNA,the accuracy of analytical solution was verified, and how impact force varies as velocity and load was concluded. Vibration frequencies of impact response were furtherly analyzed, and reasons for the changes of impact forces were studied. Research conclusions provide reference for design and applications of pneumatic cylinders.

impact force of pneumatic cylinder; analytical solution; LS-DYNA simulation; frequency analysis

杜群贵,男,1965年生。华南理工大学机械与汽车工程学院教授、博士研究生导师。主要研究方向为现代机电工程设计与控制。孙智权，男，1991年生。华南理工大学机械与汽车工程学院硕士研究生。黄崇溪，男，1990年生。华南理工大学机械与汽车工程学院硕士研究生。翟晓晨，男，1988年生。华南理工大学机械与汽车工程学院博士研究生。

2015-04-10

TH138.51;O326

10.3969/j.issn.1004-132X.2016.08.011