对称双栅高斯掺杂应变Si金属氧化物半导体场效应管的二维解析模型

李劲，吴笑峰，席在芳，胡仕刚，李目

（湖南科技大学 信息与电气工程学院，湖南 湘潭，411201）

对称双栅高斯掺杂应变Si金属氧化物半导体场效应管的二维解析模型

李劲，吴笑峰，席在芳，胡仕刚，李目

（湖南科技大学 信息与电气工程学院，湖南 湘潭，411201）

基于扩散、阈值调整和离子注入等工艺过程导致器件的沟道区的掺杂分布不均匀，提出对称双栅高斯掺杂应变硅 MOSFET器件，并对其相关特性进行研究。通过对沟道二维泊松方程求解建立该器件结构的表面势和阈值电压模型，分析弛豫SiGe层的Ge组分和掺杂偏差σn对表面势和阈值电压的影响。此外，还对比分析高斯掺杂对称双栅应变硅MOSFET器件和均匀掺杂对称双栅应变硅MOSFET器件的表面势和阈值电压。研究结果表明：阈值电压随应变Si膜中Ge组分的增加而降低；表面势和阈值电压随偏差σn的增加而减小；高斯掺杂对称双栅应变硅MOSFET器件和均匀掺杂对称双栅应变硅MOSFET器件的表面势和阈值电压相差较大，表明非均匀掺杂对器件表面势和阈值电压等影响较大。

高斯掺杂；应变Si； 阈值电压

几十年以来，随着MOSFET器件的尺寸不断缩小到深亚微米甚至纳米尺度，短沟道效应、漏致势垒降低效应和低驱动电流现象对器件性能的影响性能愈来愈显著。双栅MOSFET器件是一种极具应用前景的器件。双栅器件不仅可以很好地抑制短沟道效应、DIBL效应，降低亚阈值漏电流，具有理想的亚阈值斜率，而且不需要采用较高的沟道掺杂浓度就可以提高载流子迁移率，降低掺杂涨落及偏差对器件性能的影响，还可以提高沟道导电能力，提高器件电流驱动能力和栅控能力［1-3］。应变硅技术是利用衬底材料和外延材料的晶格失配产生的张应变或压应变效应获得具有特殊性能的应变材料，使应变 Si 中的电子和空穴的迁移率得到显著提高，从而提高MOS器件的相关特性。同时，应变硅技术能与常规工艺有良好的兼容性， 已得到广泛研究和应用［4-6］。MAHATO等［7-10］对双栅应变硅SOI MOSFET器件进行了研究， 然而，这些研究都假设器件均匀掺杂，但实际上在掺杂工艺过程中扩散和阈值调整导致器件的沟道区的掺杂分布不均匀。需特别指出的是：离子注入技术提供的是最常见的掺杂的波动范围 Rn和掺杂的偏差 σn的高斯分布［6， 11］。这种不均匀掺杂分布使器件的特性和均匀掺杂器件的特性有较大差别，本文作者对对称双栅高斯掺杂应变Si MOSFET进行研究。 采用的沟道电势抛物线近似并通用边界条件求解二维泊松方程，建立全耗尽条件下对称双栅高斯掺杂应变Si MOSFET的表面势和阈值电压二维模型。采用该模型分析弛豫SiGe层中Ge 组分、偏差σn的影响， 以便为器件设计提供参考。最后， 对高斯掺杂应变Si MOSFET器件与均匀掺杂 SOI MOSFET器件的表面势和阈值电压进行对比研究，将模型所得结果与数值仿真结果相比较。

1　表面势模型

图1所示为对称双栅高斯掺杂应变硅MOSFET的结构示意图。假设沟道区水平方向均匀掺杂，垂直方向高斯掺杂，掺杂浓度为NA（x），其表达式为［6］

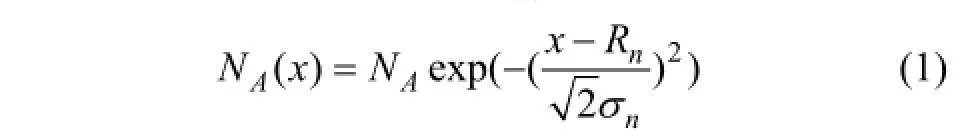
其中：NA为掺杂浓度峰值，掺杂波动范围 Rn掺杂偏差σn。

忽略固定氧化层电荷对沟道电势的影响，考虑短沟道，则弱反型时沟道电势分布可以用二维泊松方程表示为［12-15］

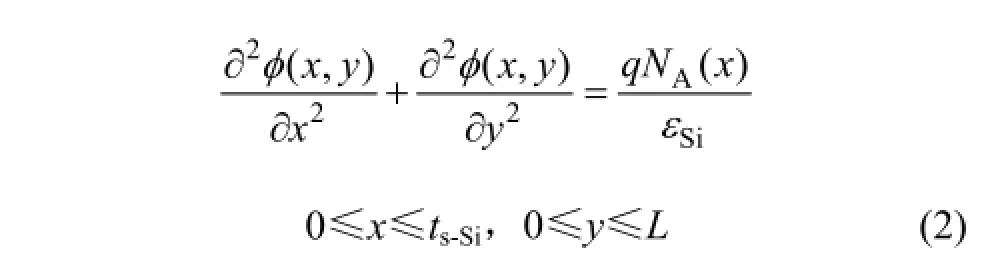
其中：εSi为硅的介电常数；ts-Si为应变硅膜厚度；L为器件的沟道长度。

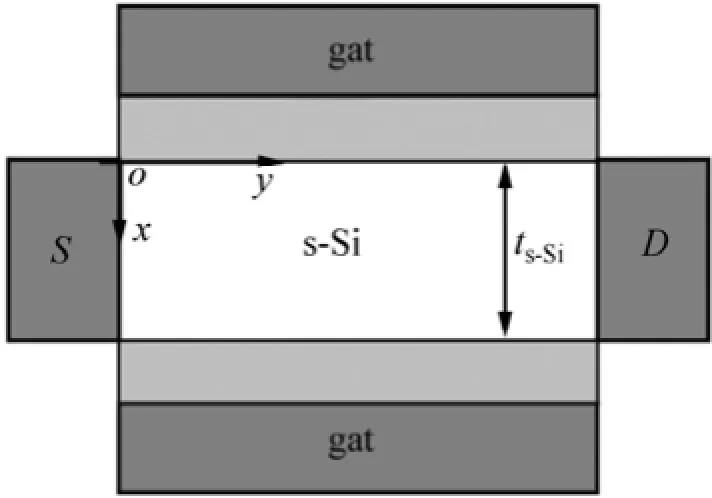
图1　对称双栅高斯掺杂应变硅MOSFET的结构示意图Fig. 1　Schematic structure of DG MOSFET with vertical Gaussian doping profile

1） 根据应变硅层与前栅介质层的电通量连续，得

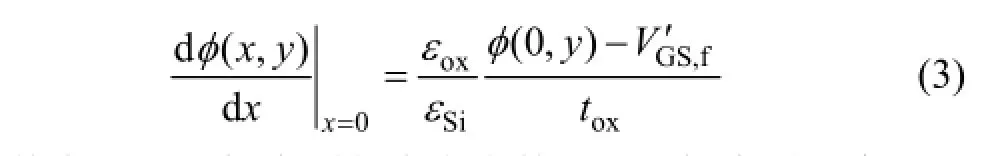
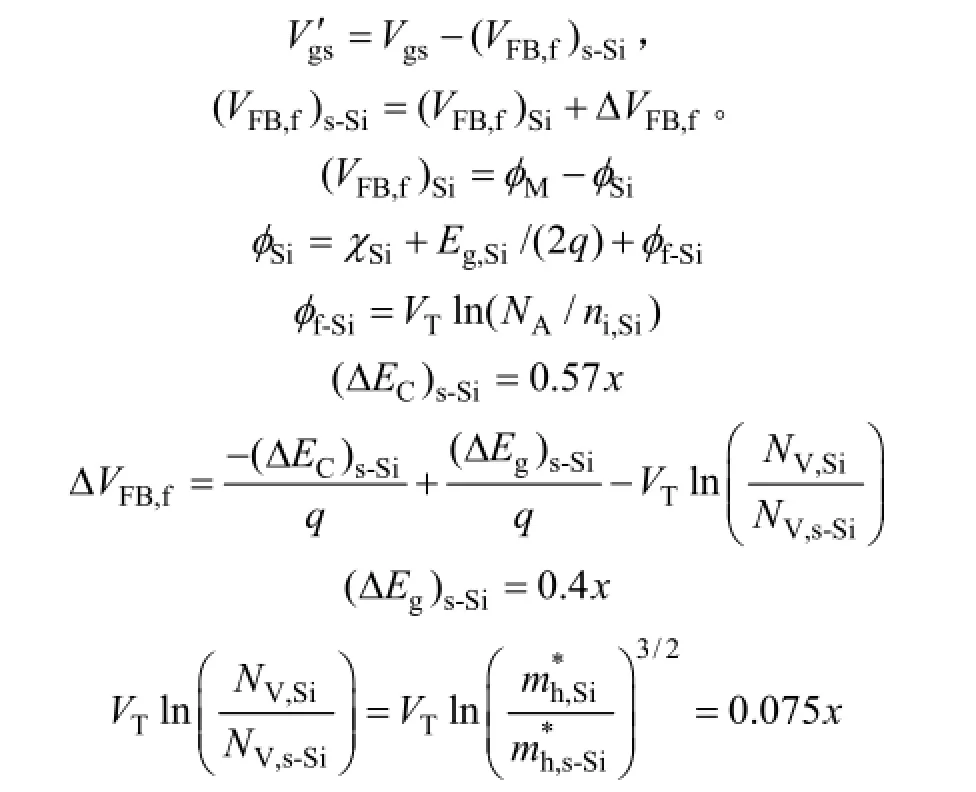
其中：εox为栅介质的介电常数；tox为栅介质厚度。由于应变的作用器件的其相应的参数得到修正［17-18］：φSi为功函数；φM为金属栅的功函数；VT为热电势；VFB，f为平带电压；Vgs为栅源电压， ΔVFB，f为平带电压的修正值，（VFB，f）s-Si为应变硅的平带电压，x为Ge组分即应变量。

2） 根据应变硅层与背栅质层的电通量连续， 得

3）电势在沟道表面处连续，即表面势。

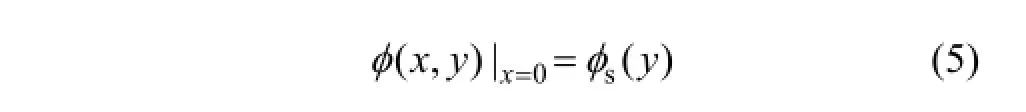
其中： φs（y）为沟道的表面势。引入新的变量 τ，。方程（1） 和边界条件（3）～（5） 修正为：

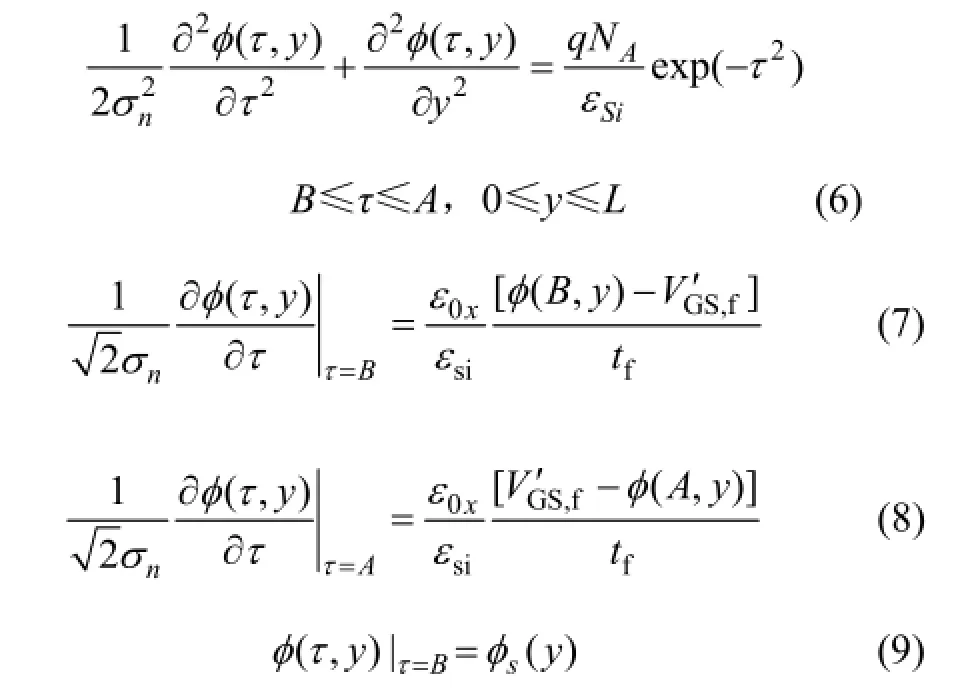
其中：c0（y），c1（y）和c2（y）仅是y的函数，其值由修正的边界条件（7）～（9）决定。

为误差函数。

通过边界条件（7）和（8），可得 c0（y），c1（y）和 c2（y）的表达式。将其代入式（10） 后再代入式（6），令y=0，可得表面势方程：

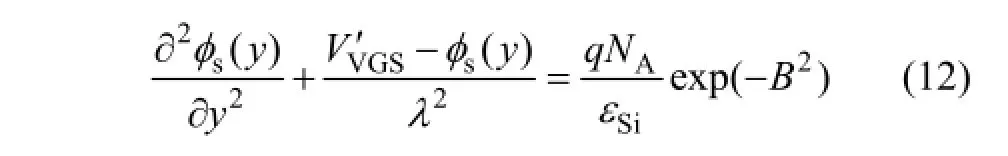
方程（12）是简单的二阶常微分方程，其解的形式如下：

其中：K1和K2为任意常数。

1） 源区的边界条件为

考虑到应变相应的参数得到修正［13-14］：

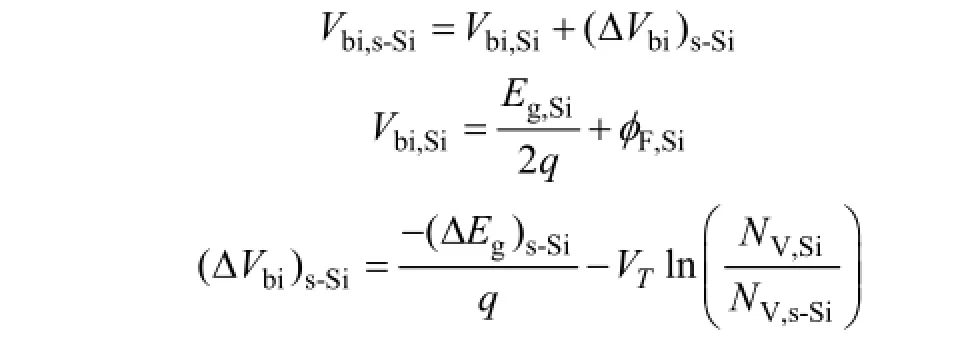
2） 漏区的边界条件为

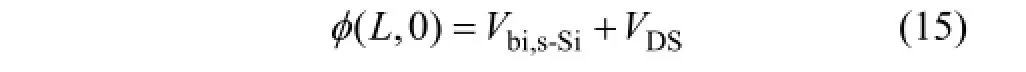
其中：VDS为漏源电压。通过源区和漏区边界条件可以确定式（6）中的K1和K2分别为：

其中：

其中： Vbi，ep为应变硅的内建电势 Vbi，s-Si及掺杂浓度NA有关的物理量； w1和w2为跟 Vbi，ep和 VDS及栅长L有关的物理量；u1和 u2为跟栅长L有关的物理量。

沿沟道的电场决定了电子的通过沟道的输运速度，金属栅下的电场为

2　阈值电压模型

表面势的最小值决定整个沟道的阈值电压Vth。由式（13）得

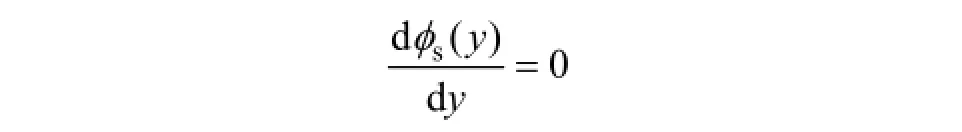
得到沟道最小表面势及其位置：

阈值电压定义为φS，min等于沟道中费米势的2倍，即 φs，min=2φF，Si时的栅源电压。考虑到应变，表面势的最小值修正为［13-14］

将式（21）代入式（19）得到阈值电压：

3　结果分析与讨论

采用下列参数对所建表面势模型和阈值电压模型进行分析和验证。栅极采用功函数 φM=4.77 eV的金属材料（如 TiN），栅氧厚度 tox=3 nm，应变硅膜厚度ts-Si=10 nm，掺杂浓度NA=1×1018cm-3， 掺杂波动为Rp=5 nm，掺杂偏差σn为2，3和5 nm，应变量x为0，0.2，0.4；栅长L=70 nm。

图 2 所示为弛豫层的 Ge 组分 x不同时应变硅层表面沿沟道方向的表面势分布情况。从图2可以看出：在源端和漏端表面势随弛豫层中Ge 组分的增加而减小，Ge 组分越大，其表面势越小；在沟道中间段，其表面电势则随 Ge 组分的增加而增加，Ge 组分越大，其表面势越大，意味着其阈值电压较低。从图 2 可以明显看出垂直沟道方向表面势分布呈抛物线形状，证实了抛物线分布假设的正确性。

图2　不同Ge 组分下沿沟道方向的表面势Fig. 2　Surface potential with horizontal distance along channel for different effective Ge mole fractions

图3所示为不同掺杂偏差σn下沿沟道方向的表面势分布。从图3可看出：由于偏差σn导致表面势的弯曲程度发生了变化，σn越小，弯曲越小，其表面势随着σn的增加而减小；垂直沟道方向的表面势分布呈抛物线形状，进一步证实了抛物线分布假设的正确性。

图 4 所示为高斯掺杂和均匀掺杂 DG MOSFET结构器件表面势对比。从图4可以看出：高斯掺杂的DG MOSFET 结构器件的表面势较均匀掺杂的 DG MOSFET 结构器件的表面势要大，因此，必须建立高斯掺杂的DG MOSFET 结构器件的相关模型。

图 5 所示为不同 Ge 组分x时高斯掺杂应变硅DG MOSFET器件阈值电压变化情况。在特定沟道长度下，应变沟道的应变量越大，其阈值电压越小。这是由于弛豫层中Ge 组分增加，应变Si 应变加强，禁带宽度进一步减小，ΔEc增大，本征载流子浓度和沟道电子面密度均提高，从而导致阈值电压减小；同时，随着沟道的不断缩小，器件的阈值电压降落比较明显；当沟道长度小于40 nm时，阈值电压随沟道长度减小程度明显降低。

图3　不同偏差σn下沿沟道方向的表面势Fig. 3　Surface potential with horizontal distance along channel for different straggle σn

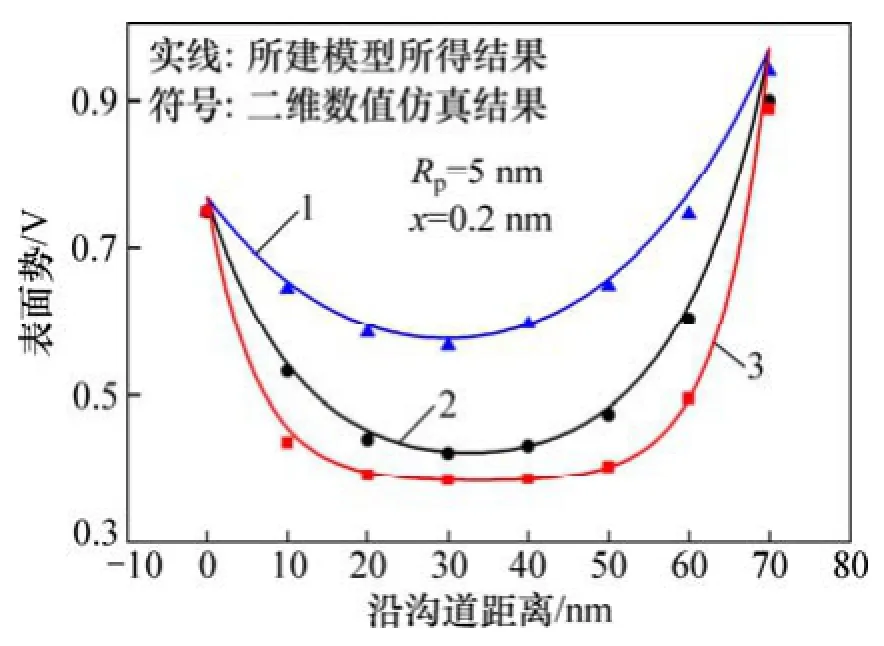
图4　高斯掺杂和均匀掺杂DG MOSFET 结构器件表面势对比Fig. 4　Comparison of surface potential of DG MOSFE with Gaussian doping and with uniform doping

图 6所示为不同偏差 σn下高斯掺杂应变硅 DG MOSFET器件阈值电压变化情况。从图6可以看出：随着偏差σn的增加，高斯掺杂应变硅DG MOSFET器件阈值电压略增加，并随着偏差σn的增加，在沟道长度较短的情况下阈值电压的降落明显减少。

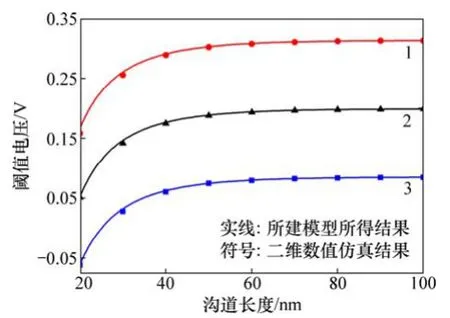
图5　不同Ge 组分下高斯掺杂应变硅DG MOSFET器件阈值电压Fig. 5　Threshold voltage of DG MOSFE for different effective Ge mole fractions

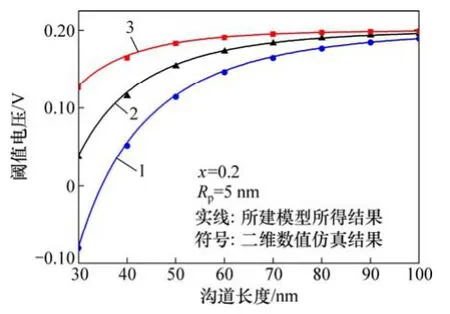
图6　不同偏差σn下高斯掺杂应变硅DG MOSFET器件阈值电压Fig. 6　Threshold voltage with horizontal distance along channel for different straggle σn

图7 所示为高斯掺杂和均匀掺杂DG MOSFET结构器件阈值电压对比。从图7 可以看出：高斯掺杂的DG MOSFET 结构器件的阈值电压较均匀掺杂的DG MOSFET 结构器件的阈值电压大，而且其在沟道较短时阈值电压降落较均匀掺杂DG MOSFET器件阈值电压降落明显。

图 8 所示为 Ge 组分 x=0.2 时，在不同偏差 σn下，DIBL随沟道长度L的变化曲线。从图8可以看出：高斯掺杂DG MOSFET器件的漏致势垒降低效应DIBL随着沟道长度的增加迅速趋近于0，并且随着偏差σn的增加，高斯掺杂DG MOSFET器件的DIBL更快趋近于0。

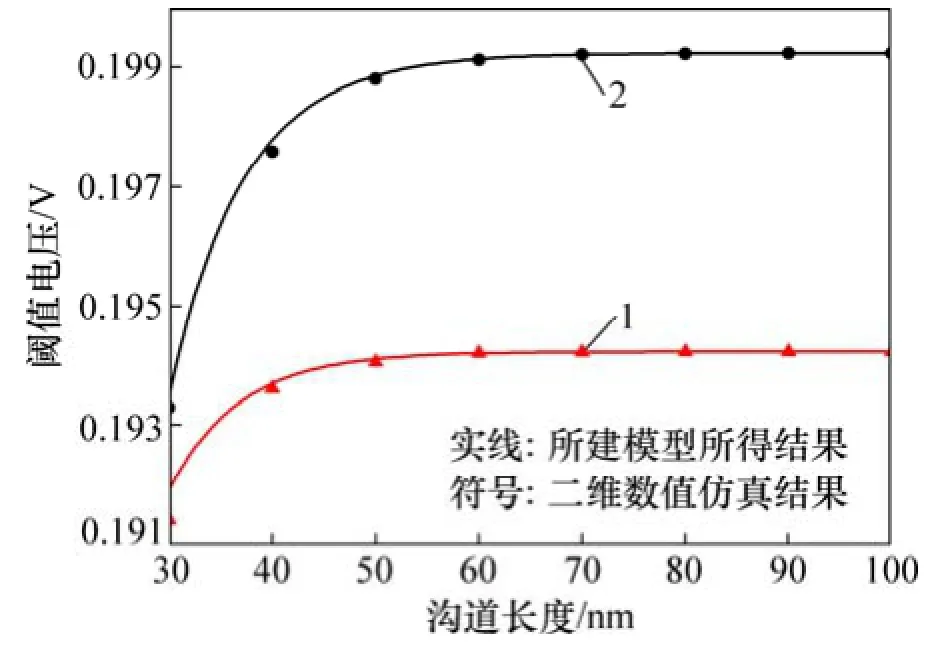
图7　高斯掺杂和均匀掺杂DG MOSFET结构器件阈值电压对比Fig. 7 Comparison of threshold voltage of DG MOSFET with Gaussian doping and with uniform doping

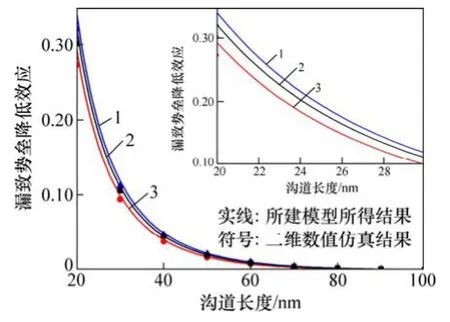
图8　不同偏差σn下DIBL 随沟道长度变化曲线Fig. 8　Relationship between DIBL and channel length L for different straggle σn

4　结论

1） 建立了对称双栅高斯掺杂应变硅SOI MOSFET器件中高斯掺杂的沟道的二维泊松方程，通过求解二维泊松方程， 得到了表面势和阈值电压的解析模型。

2） 随着偏差 σn的增加，表面势不断降低，其阈值电压的降低幅度也不断减小，DIBL效应也变得更小。在特定的沟道长度情况下，应变沟道的应变量越大，其阈值电压越小。

3） 高斯掺杂对MOS器件的阈值电压的影响比对均匀掺杂MOS器件阈值电压的影响大。

［1］ HE Jin， LIU Feng， ZHANG Jian， et al. A carrier-based approach for compact modeling of the long-channel undoped symmetric double-gate MOSFETs［J］. IEEE Transactions Electron Devices，2007， 54（5）： 1203-1207.

［2］ CHIAGE T K， CHEN M L. A new analytical threshold voltage model for symmetric double-gate MOSFETs with high-k gate dielectrics［J］. Solid State Electron， 2007， 51（1）： 387-390.

［3］ ORTIZ-CONDE A， GARCÍA-SÁNCHEZ F A， MUCI J， et al. A review of core compact models for undoped double-gate SOI MOSFETs［J］. IEEE Transactions Electron Devices， 2007， 54（1）：131-135.

［4］ BANNA S R， CHAN PH C H， KO P K， et al. Threshold voltage model for deep-submicrometer fully depleted SOI MOSFET’s［J］. IEEE Transactions Electron Devices， 1995， 42（11）： 1949-1952.

［5］ JOACHIM H O， YAMAGUCHI Y， ISHIKAWA K， et al. Simulation and two-dimensional analytical modeling of subthreshold slope in ultrathin-film SOI MOSFET’s down to 0.1 μm gate length［J］. IEEE Transactions Electron Devices， 1993，40（10）： 1812-1819.

［6］ ZHANG G H， SHAO Z B， ZHOU K. Threshold voltage model of short-channel FD SOI MOSFETs with vertical Gaussian profile［J］. IEEE Transactions Electron Devices， 2008， 55（3）：803-808.

［7］ MAHATO S S， CHAKRABORTY P， MAITI T K， et al. DIBL in short channel strained-Si n-MOSFET［C］//IEEE Proceedings 15th International Symposium on the Physical and Failure Analysis of Integrated Circuits （IPFA）. Singapore， 2008： 1-5.

［8］ KUMAR M J， VENKATARAMAN V， NAWAL S. A simple analytical threshold voltage model of nanoscale single-layer fully depleted strained-silicon-on-insulator MOSFETs 2006［J］. IEEE Transactions Electron Devices， 2006， 53（3）： 2500-2505.

［9］ KUMAR M， DUBEY S， TIWARI P K， et al. Analytical modeling and simulation of subthreshold characteristics of back-gated SSGOI and SSOI MOSFETs： a comparative study［J］. Current Applied Physics， 2013， 13（8）： 1778-1783.

［10］ MUKHOPADHYAY B， BISWAS A， BASU P K， et al. Modelling of threshold voltage and subthreshold slope of strained-Si MOSFETs including quantum effects［J］. Semiconductor Science Technology， 2008， 23（9）： 095017-095021.

［11］ ZHANG G H， SHAO， ZH B， ZHOU K. Threshold voltage model of short-channel FD-SOI MOSFETs with vertical gaussian profile［J］. IEEE Transactions Electron Devices， 2008， 55（4）：803.

［12］ WANG Min， KE Daoming， XU Chunxia， et al. A 2-Dsemi-analytical model of parasitic capacitances for MOSFETs with high k gate dielectric in short channel［J］. Solid-State Electronics， 2014， 92（5）： 35.

［13］ LU C C， KUEI-SHU CH L， CHE-HAO T， et al. Profiling of channel-hot-camer stress-induced trap distributions along channel and gate dielectric in high-k gated MOSFETs by a modified charge pumping technique［J］. IEEE Transactions Electron Devices， 2014， 61（4）： 93.

［14］ 韩名君， 柯导明. 超浅结亚45 nm MOSFET亚阈值区二维电势模型［J］. 电子学报， 2015， 43（1）： 94-98. HAN Mingjun KE Daoming. A 2-D potential sub-threshold model for sub-45 nm MOSFETs with ultra shallow junctions［J］. Chinese J Electron， 2015， 43（1）： 94.

［15］ TRIPATHI S. A two-dimensional analytical model for channelpotential and threshold voltage of short channel dual material gate lightly doped drain MOSFET［J］. Chin Phys B，2014， 23（11）： 8505-8510.

［16］ KUMAR P， WARI T， JIT S. Threshold voltage model for symmetric double-gate （DG） MOSFETs with non-uniform doping profile［J］. Journal of Electron Devices， 2010， 7（6）：241-247.

［17］ DJEFFAL F， MEGUELLATI M， BENHAYA A. A two-dimensional analytical analysis of subthreshold behavior to study the scaling capability of nanoscale graded channel gate stack DG MOSFETs［J］. Physica E， 2009， 41（8）： 1872-1878.

［18］ KUMAR M， DUBEY S， TIWARI P K， et al. Two-dimensional modeling of subthreshold current and subthreshold swing of double material-gate（DMG） strained-Si （s-Si） on SGOI MOSFETs［J］. Journal of Computational Electronics， 2013， 12（2）：275-278.

（编辑 陈灿华）

Two-dimensional analytical models for double-gate (DG) strained-Si metal-oxide-semiconductor field transistor with vertical gaussian doping profile

LI Jin， WU Xiaofeng， XI Zaifang， HU Shigang， LI Mu

（School of Information and Electrical Engineering， Hunan University of Science and Technology， Xiangtan 411201， China）

Considering that diffusion， threshold voltage adjustment and ion implantation process cause the device channel doping distribution to be uneven， a symmetrical double-gate strained-Si metal-oxide-semiconductor field transistor （MOSFET） with a vertical Gaussian doping profile was proposed， and the two-dimensional surface potential model and threshold voltage model for this MOSFET were studied to solve Poisson’s equation. The effects of Gaussian doping straggle parameter σnon surface potential and threshold voltage were investigated. The influence of Ge fraction in the relaxed layer on the surface potential and threshold voltage models was analyzed. Both models of DG MOSFET with Gaussian doping and uniform doping were compared， respectively. SCEs （short-channel effect） and （Drain-Induced-Barrier- lowering） DIBL were analyzed. The results show that the doping distribution has great influence on the device such as surface potential and threshold voltage.

Gaussian doping； strained Si； threshold voltage

TN302

A

1672-7207（2016）04-1203-06

10.11817/j.issn.1672-7207.2016.04.017

2015-05-10；

2015-07-22

国家自然科学基金资助项目（61474042，61404049，61376076）；湖南省科技计划项目（2013FJ2011，2014FJ2017）；湖南省教育厅资助项目（14B060，13C321）（Projects （61474042， 61404049， 61376076） supported by the National Natural Science Foundation of China； Projects （2013FJ2011， 2014FJ2017） supported by the Science and Technology Plan of Hunan province； Projects （14B060， 13c321）supported by Education Department of Hunan Province）

李劲，博士，讲师，从事半导体器件及其可靠性研究；E-mail：lijinpower@126.com