基于径向基神经网络对磨削功率预测的研究*

陈世隐,郭佳杰,黄国钦

(华侨大学制造工程研究院，福建 厦门　361021)



基于径向基神经网络对磨削功率预测的研究*

陈世隐,郭佳杰,黄国钦

(华侨大学制造工程研究院，福建 厦门361021)

将径向基(RBF)神经网络应用到工程陶瓷缓进给大切深磨削领域，建立了磨削功率随砂轮速度、工作速度、磨削深度变化的预测模型。研究结果表明：预测值与实际值最大误差为5.30%，平均相对误差为3.2%，因此，径向基神经网络能准确地预测磨削功率的变化趋势。

径向基RBF；神经网络；工程陶瓷；缓进给大切深；磨削功率；预测

随着科学技术，特别是能源、空间技术的发展，工程陶瓷以其高强度、低膨胀率、耐磨损及化学稳定性等优越的性能受到广泛关注。目前工程陶瓷材料己用于电子、航空航天、汽车、切削工具、冶金、机械、化工等高技术工程领域[1]。这些陶瓷元器件的应用是需要高的尺寸精度和表面完整性的，而且对加工表面层特性的要求很高。工程陶瓷材料是由粉末状原料制造成型后在高温下烧结而成的，不可避免会出现毛坯烧结收缩的状况，使得工程陶瓷零件需要经过机械加工才能满足尺寸、形状的公差要求和表面粗糙度要求。金刚石砂轮磨削是工程陶瓷最有效、经济的加工方法。高效深磨削作为一种先进的现代磨削技术，以极高磨削效率、极大的砂轮磨削比以及良好的工件表面完整性给传统的磨削领域带来了一场革命。

在实际工程中，由于磨削加工过程影响磨削功率的各个因素错综复杂，而磨削功率经验公式的建构方法虽简单，但其适用度范围窄，需要做大量的试验，成本高。径向基(RBF)神经网络在非线性系统的建模与辨识中有明显的优越性，将RBF应用于工程陶瓷高效深磨功率消耗的预测将不受非线性模型的限制，可以得到比较理想的结果。近年来在系统预测中应用较多的是BP网络，但BP算法用于函数逼近时，权值的调节采用负梯度下降法，存在易陷入局部极小值等缺点。径向基(RBF)神经网络具有收敛速度快，不存在局部极小点等优点，具有很强的非线性逼近能力，其输出是隐单元输出的线性加权和，在同样隐层神经元结构下网络学习效率更高[2]。

1　径向基神经网络模型

RBF网络的基本思想是：用RBF作为隐单元的“基”构成隐含层空间，这样就可以将输入矢量直接(即不需要通过权接)映射到隐空间。当RBF的中心点确定以后，这种映射关系也就确定了。而隐含层空间到输出空间的映射是线性的，即网络的输出是隐单元输出的线性加权和。此处的权即为网络可调参数。由此可见，从总体上看，网络由输入到输出的映射是非线性的，而网络输出对可调参数而言却又是线性的[3]。

径向基神经网络可分为正则化网络和广义网络，本文中用到的是正则化网络。正则化径向基函数网络由三层组成，第一层由输入节点组成，输入节点的个数等于向量x的维数m;第二层属于隐含层，由直接与输入节点相连的节点组成，一个隐含节点对应一个训练数据点，因此其个数与训练数据点的个数相同。正则化径向基网络结构[4]如图1所示。

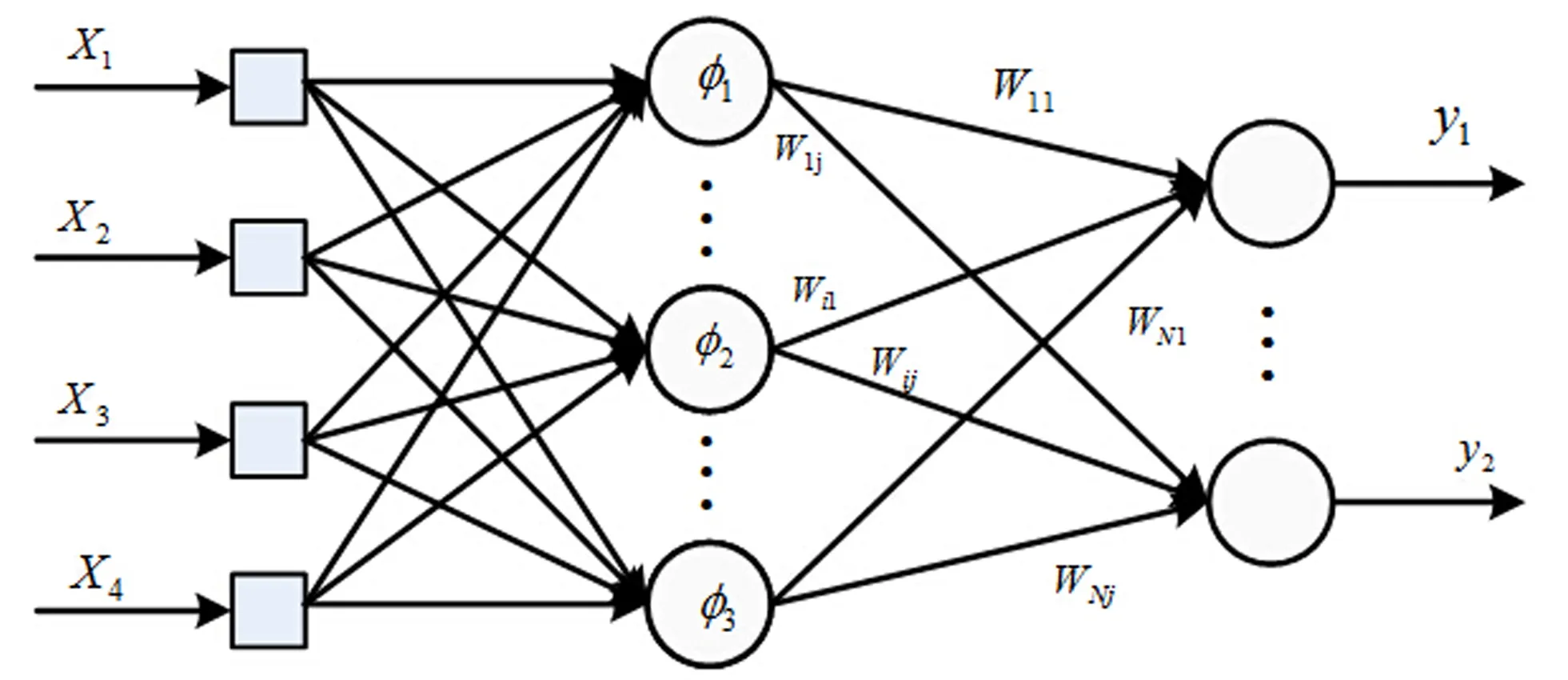
图1　正则化径向基网络结构Fig.1　Regularized RBF neural network structure

常见的径向基函数都是径向对称的，自变量在偏离中心位置时函数值都快速下降，下降越快，选择性越强。其中最为常用的是高斯函数。径向基网络是一种局部逼近网络，对每个训练样本只需要对少量的权值和阀值进行修正，因此训练速度快。径向基神经网络的神经元模型[5]如图2所示：

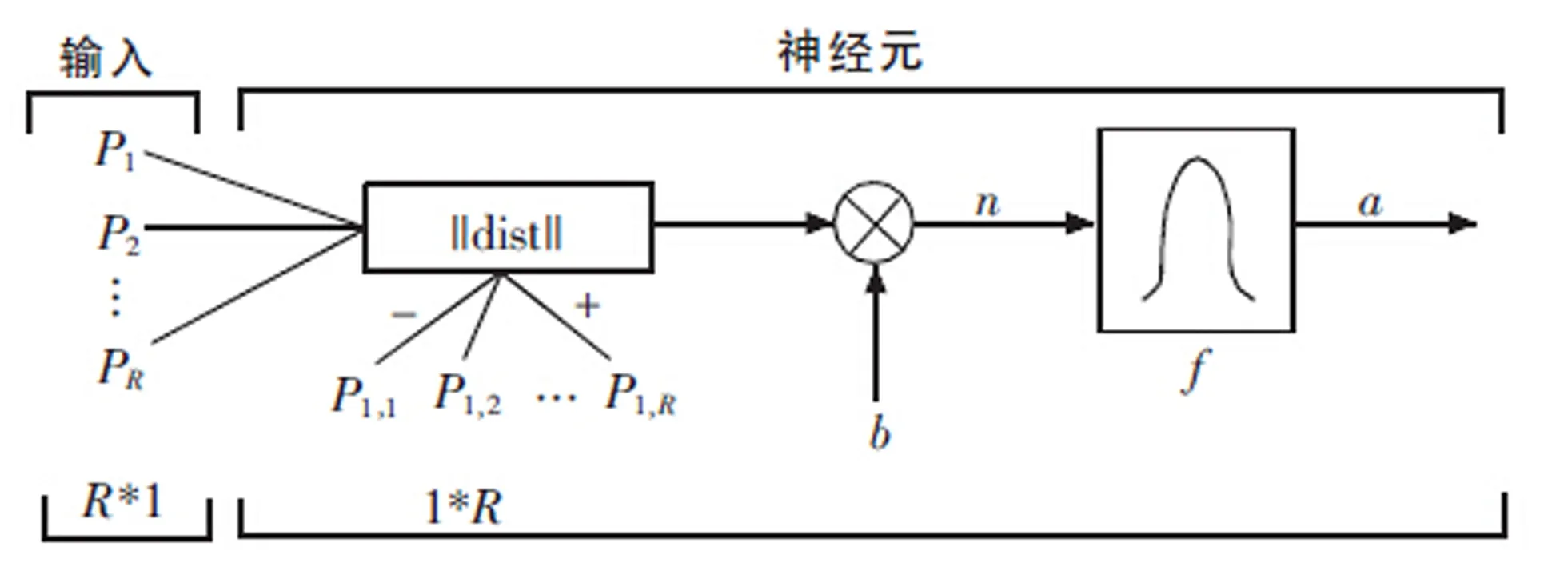
图2　径向基神经元模型Fig.2　RBF neuron model

当网络输入层自变量n为0时，高斯函数输出最大值1;随着权值和输入向量距离的减小，径向基层的输出是递增的，即径向基函数对输入信号在局部产生响应。当n靠近函数的中央时，隐含层将产生较大的输出，能以任意精度逼近任一连续函数。径向基神经元模型同样如图2所示，其中b为阀值，用于调整神经元的灵敏度。

2　工程陶瓷高效深磨功率消耗预测的实现

径向基函数网络一经创建，不需要训练就可以直接使用。输入样本向量首先与权值向量相乘，再输入到隐含层节点中，计算样本与节点中心的距离。该距离经过径向基函数(通常为高斯型函数)的映射后形成隐含层的输出，再输入到输出层，各个隐含层节点的线性组合形成了最终的网络输出。利用径向基网络进行砂轮磨削功率消耗预测的流程框图如图3所示。

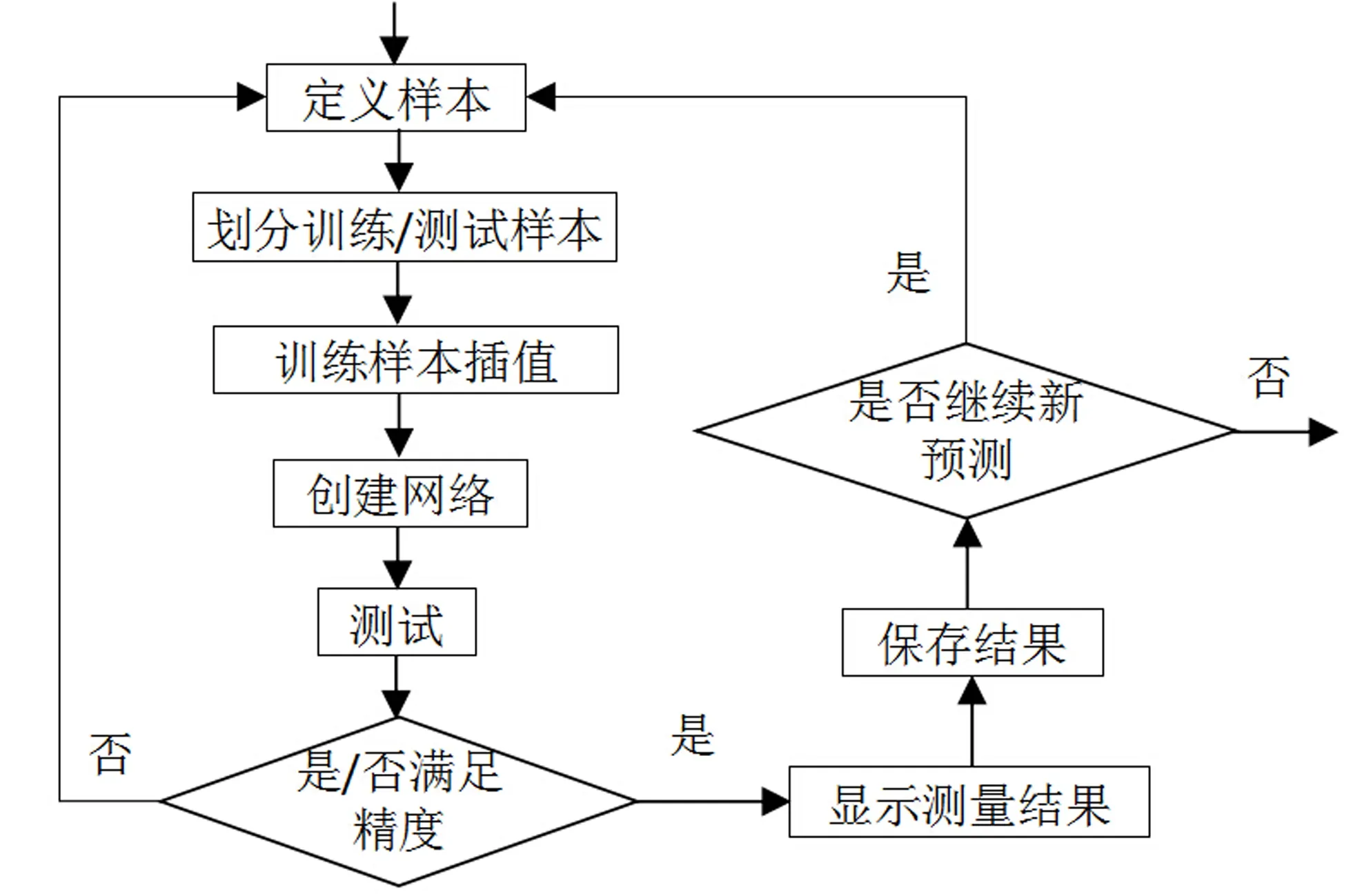
图3　流程框图Fig.3　Flow diagram

2.1网络的创建

在工程应用中使用已选定的砂轮对工程材料进行磨削时，砂轮速度vs、工作速度vw、磨削深度ap是影响磨削功率变化的最大的三个因素。在对磨削功率消耗径向基神经网络进行建模时，RBF网络的输入层为砂轮速度vs、工作速度vw、磨削深度ap，输出层为磨削功率P。

采用钎焊金刚石砂轮磨削氧化铝陶瓷，实验结果如表1所示。前18组数据用于径向基神经网络训练数据，后6组作为预测数据。为了充分利用训练样本，对18份训练样本进行二维插值，将样本数量增加到100份。这里用到了MATLAB的二维插值函数interp2。先将训练输入向量与对应的目标输出合并作为一个4×18矩阵，经过插值，得到4×100矩阵，最后再将其拆分为3×100矩阵作为训练输入，1×100的行向量作为训练样本的输出。对训练样本插值的MATLAB程序代码如下：

N=size(trainx,2);

X=[trainx;trainy];

[xx0,yy0]=meshgrid(1:N,1:4);

[xx1,yy1]=meshgrid(linspace(1,N,100),1:4);

XX=interp2(xx0,yy0,X,xx1,yy1,'cubic');

trainx=XX(1:3,:);

trainy=XX(4,:);

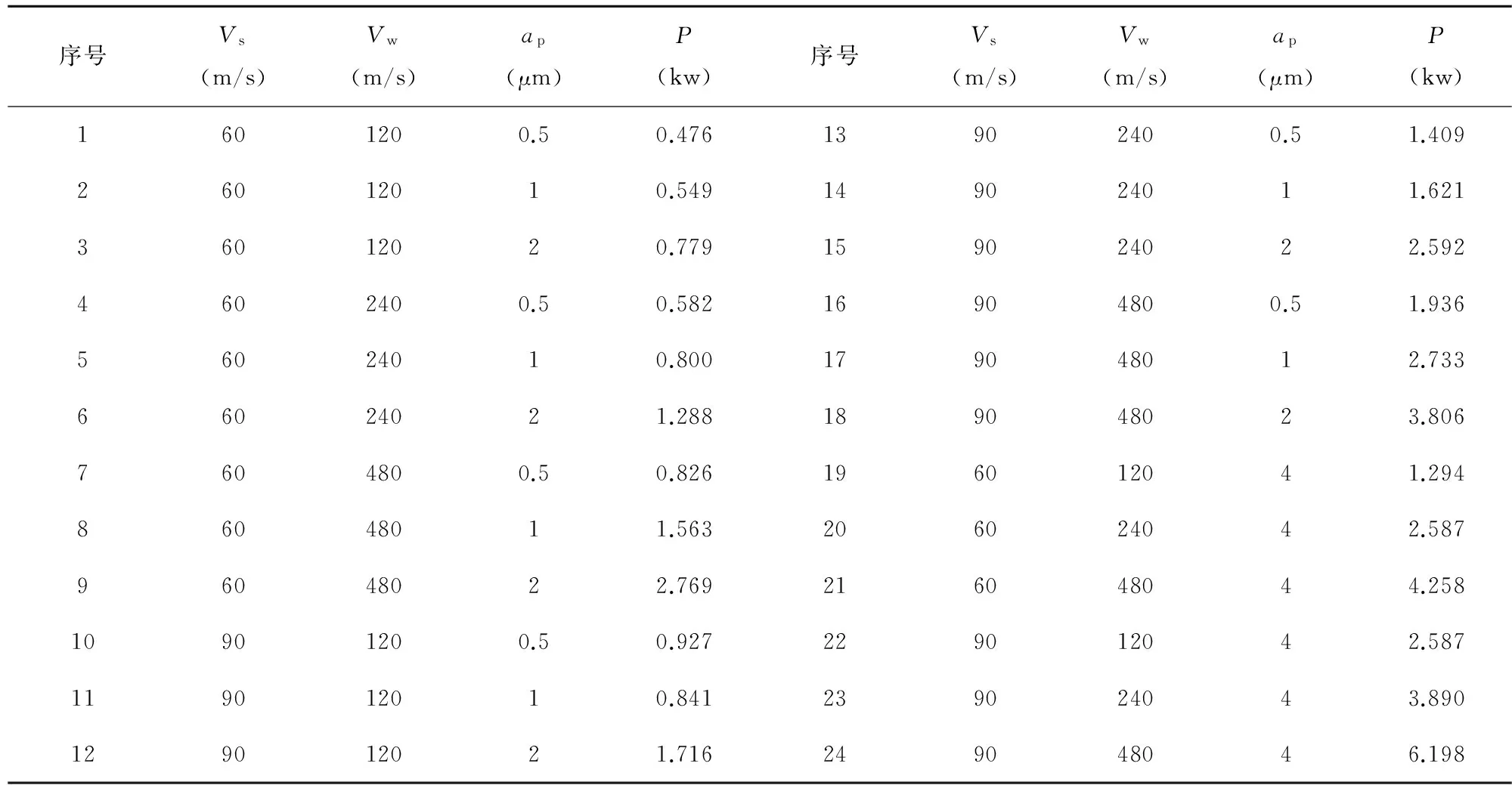
表1　磨削功率实验数据

2.2参数的确定

选用合适的径向基函数，确定基函数的中心、宽度以及隐含层到输出层之间的权值，是构造径向基网络的关键。一般需预先确定径向基函数数目，RBF的中心从训练集随机选取，或由训练集以某种学习方式确定。本实验用MATLAB神经网络工具箱构建网络，利用函数newrb创建神经网络时，开始是没有径向基神经元的，newrb是逐渐增加径向基神经元数的，可以获得比newrbe更小规模的径向基网络，所以本文选取函数newrb来创建一个高精度的PBF神经网络。newrb函数所建立网络的训练误差平方和目标设定为1e-8,径向基扩展系数spread根据误差情况选取，不同的训练集取值可以不同，通过误差值调整spread值，并使误差达到最小。本文spread取100，误差容限为1e-8，最大神经元个数为101。调用函数newrb，系统将会逐渐增加神经元，使训练误差逐渐减小，直到误差小于容限。误差下降曲线如图4所示。

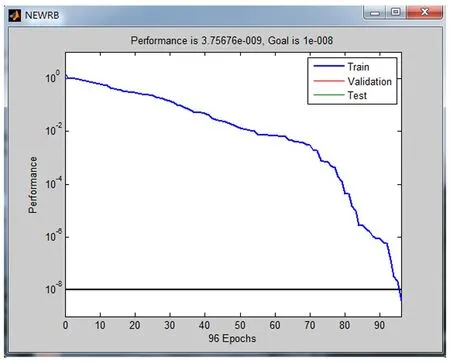
图4　误差下降曲线Fig.4　Decline curve of deviation

实际最终使用了96个神经元节点，训练误差为10-9数量级。用view(net)命令可以看最终的径向基网络结构，如图5所示。

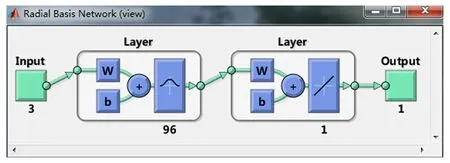
图5　RBF网络结构图Fig.5　RBF network structure

2.3预测结果及分析

在网络应用于工程之前，必须通过实验数据检测其预测精度。利用序号为19-24的实验数据对网络预测值进行检验其预测精度，预测结果与试验结果对比，得到的预测数据如表2所示。从表2中可以明显地看出，预测值与真实值是非常接近的。而且预测值与真实值的变化趋势完全一致。由验证试验可知，预测值与实际值最大误差为5.30%，平均相对误差为3.2%，因此，有理由认为，径向基网络准确地预测了磨削功率变化趋势。

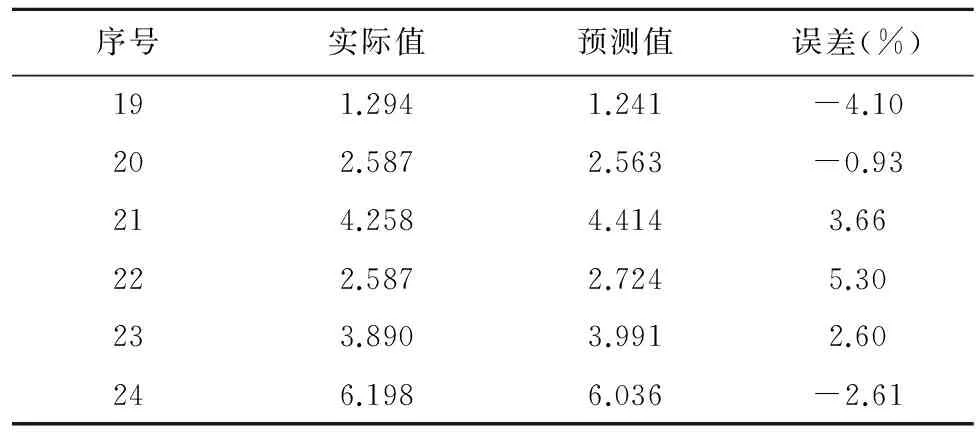
表2　预测值及误差值

3　结论

应用RBF神经网络建立了砂轮速度、工作速度、磨削深度三因素对磨削功率的预测模型。通过实验数据对所建立的RBF网络模型进行训练，并从理论和试验两方面进行了验证。预测结果表明预测值和真实值的相对误差满足工程应用要求，这对于降低实验成本，研究磨削机理有很重大的意义。

[1]贠自明.金刚石钎焊砂轮磨削工程陶瓷的试验研究[D].南京：南京航空航天大学，2005.

[2]尤文坚，叶雪英，唐仕云.基于径向基神经网络农机数量预测的研究[J].中国农机化学报，2013,34(2)：38-41.

[3]陈明.神经网络原理与实例精解[M].北京：清华大学出版社，2013.

[4]刘志杰，季令，叶玉玲，耿志民.基于径向基神经网络的铁路货运量预测[J].铁道学报，2006,28(05)：1-5.

[5]汪洋，宇仁德，闫建华.基于径向基函数神经网络的交通事故预测[J].交通标准化，2009，208：1-4.

Research on Prediction of Grinding Power Based on RBF Neural Network

CHEN Shi-yin, GUO Jia-jie, HUANG Guo-qin

(InstitutionofManufactureEngineering,HuaqiaoUniversity,Xiamen,Fujian,China361021)

The application of radial basis function(RBF) neural network to engineering ceramics creep-feed has set up a prediction model for deep grinding field. According to the model, the grinding power changes as the grinding wheel speed, working speed and grinding depth change. Result shows that the maximum deviation between predicted value and real value is 5.30% and the average relative deviation is 3.2%. This means that the RBF neural network can accurately predict the change trend of grinding power.

RBF; neural network; engineering ceramics; deep creep-feed; grinding power; prediction

2016-05-18

国家自然科学基金(51235004, 51575198)，华侨大学研究生科研创新能力培育计划资助项目(1400203002)

陈世隐(1992-)，男，硕士研究生。研究方向：高效精密加工。

TQ164

A

1673-1433(2016)04-0033-04

引文格式：陈世隐,郭佳杰,黄国钦.基于径向基神经网络对磨削功率预测的研究[J].超硬材料工程，2016，28(4)：33-37.