傅里叶热传导方程和牛顿冷却定律在流体热学研究中的数学模型应用

李昂，王岳，陶然（吉林大学，吉林省长春市，130021）



傅里叶热传导方程和牛顿冷却定律在流体热学研究中的数学模型应用

李昂，王岳，陶然
（吉林大学，吉林省长春市，130021）

柱形流体热传导过程对于研究自然界热流体有着重要的实际意义.本文以浴缸中流动的热水为模型。通过利用傅里叶—维热传导方程和插值拟合的手段，辅以利用牛顿冷却定律对流体边缘热传导过程优化，将三维问题一维化，探讨其热量分布和温度平衡的过程，从而为实际流体热学的研究提供一些方法上的思路。

流体；热量分布；傅里叶方程

引言

在流体热学中，流体与周围环境的热交换过程十分复杂［1］。目前比较主流计算热传导的方法是傅里叶热传导方程，该方程在一维、二维情况下可以对于热量的分布情况进行比较准确的计算；然而在三维情况下，因为方程难以解出而被成为“百万美金难题”。

本文以柱形流体热传导过程为基础，利用傅里叶—维热传导方程和插值拟合的手段，应用牛顿冷却定律对流体边缘热传导过程优化［2-3］，将三维问题实现一维化处理，将实践与理论相结合，探讨了热量分布和温度平衡的过程。

1　热传导模型背景和提出

在柱状流体的实际流动过程中，从宏观看，其热能的散失来源于热传导的几个过程，从流体向周边固体传导，气体传导或者向温度更低的液体传导为最典型的三种情况，其中流体内的传导过程即为高温处向低温处的传导，其符合傅里叶热传导方程。流体与固体之间的传导可以使用牛顿冷却定律计算传导的热量，流体与气体之间热传导过程可以“空气墙”思想利用牛顿冷却定律计算传导热量［4］。通过对于热量的计算可以得到体系冷却的时间和距离，也可以探讨体系温度保持平衡的基本条件。本文以2016年美国数学建模竞赛A题“浴缸模型”为研究背景，这个浴缸通过注入热水和排出另一端的较低温热水达到温度平衡状态，通过对于散失热量的研究探讨热水注入的流量来研究浴缸温度平衡的过程，从而扩展到实际的应用工作以及其他领域的研究。

2　热传导模型的具体建立过程

2.1热量等效模型

在整个浴缸散热体系中，体系中流动的热水在入口处和出口处的温度有所变化，假设入口处为T1，出口处为T2。那么显然T1＞T2。如果把热水作为研究对象，热水前后温度的变化显然是由于整个浴缸体系散热造成的，输入的热量为

其中:

因此Qinput=C（T2-T1）ρT1φt，上式中：t代表流体流动的时间，φ代表流量，ρ为流体密度，C为比热容。

由于注入体系中的热量和体系中散失的热量相等，才能使浴缸的温度守恒，达到恒温浴缸的目的，因此，在进一步计算散热的时候，我们可以用Qinput代表总散热。那么不难推断维持体系温度平衡的流量为：

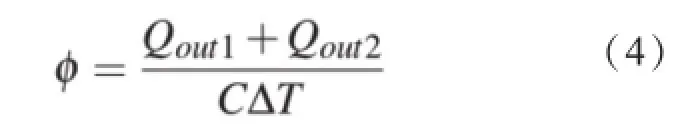
2.2具体散热模型

2.2.1流体—空气界面散热的参数归一模型

流体在与空气界面进行热交换的过程，是一个十分复杂的过程，其与流体的流速，表面粘滞系数流体密度和流体液压等等都有着重要的关系，但是有一点可以肯定，当体系平衡稳定的时候，这些参数的值都在一个固定的范围内微小变化，因此我们可以把这些参数归一化，即把这些参数的影响有一个新的变量表示——综合影响因子Ka。根据前人研究，Ka代表着单位时间，单位面积流体在空气接触面温度下降一度热量传递，那么在空气处散失的热量就可以用以的公式计算［5］：

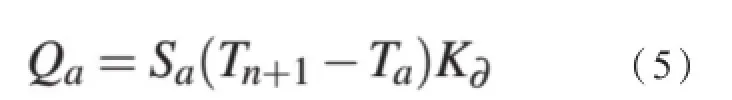
这里采用微元法，通过计算每个点元的散失热量来近似的等效于连续分布的流体热量散失情况。根据前人经验，Ka的计算方法如下：

显然，这种计算方法过于繁琐复杂，下文我们将利用一个前人总结的经验公式进行此参数的计算。

2.2.2流体—固体热传导模型

在实际的浴缸散热模型中，热水在与空气的接触面散热量是最大的，但仍然要考虑到缸壁的散热，在这一模型中，我们采用的基本理论是牛顿冷却定律，具体参照的模型为“双层玻璃窗”模型。牛顿冷却定律计算散失的热量，其重要的条件就是要得出热量在固体中传导的具体距离，根据实验的经验结果显示，在2cm厚度亚克力材料中，温度通过浴缸传导后，在距离浴缸1cm左右处的外壁空气处热量彻底散失，因此我们可以假设2cm厚度的浴缸和1cm厚度的空气为两个隔离（图1），分别利用牛顿冷却定律计算。假设浴缸外壁的温度为Tx，那么可以肯定的是，热量从浴缸内部传导到浴缸外壁，以及由浴缸外壁传导到空气处是相等的，利用这个平衡公式可以计算出Tx，从而得到浴缸外壁处散失的热量。

图1　缸壁热传导的实际过程

3　热传导模型的具体计算以及傅里叶热传导方程一维化的应用

3.1一维化思想

图2　将三维的流体流动过程一维化

一维化思想的核心就是把三维问题一维化，通过利用等效法，对于截面进行研究，把截面的各种因素归一到一个点处，那么整个流体的模型其实就是一个线性分布的点集（图2），从而通过研究点与点的关系而推论出整个柱形流体的实际温度分布情况。

3.2傅里叶热传导方程的一维形式

显然，为了计算每个位置的散热量，我们要计算出每个位置的具体热量，在一个恒温模型中，温度和时间的关系为：

如果我们仅仅考虑温度不随流动的具体位置变化，这个方程可以改变为：

那么，在这组方程中，Q即代表了两个温度不同的点在接触处传导的热量，而f即为前式中的隐函数f（x）。

以上即为傅里叶热传导模型的基本框架，显然，通过对于Q的计算，我们就可以求出相应的隐函数f，再利用积分便可以求出这一段微元的温度情况。对于Q的计算，我们进入了下一个模型。

3.3牛顿冷却定律对散热情况的求解

在该式中，A为截面面积，△t为两个点元之间的温度差，h为热导系数，显然：

显然这个方程是一个递归过程，通过Matlab计算每一点处的温度，然后通过插值拟合，得到温度分布的曲线（图3）。

图3　浴缸内部温度实际拟合曲线

3.4 具体散热情况的计算

3.4.1流体与空气界面散热

在流体与空气的分界处，流体的散热满足以上的公式，其中Tn+1为流体每一个位置处的温度，Ta为空气温度，Sa为水面面元的面积，而Ka代表水面散热系数，可以用如下公式求解

其中Ka水面散热系数代表着水面温度每下降一度所散失的热量，而散失的热量 L包括蒸发热，对流热和辐射热三部分，以蒸发散热最为主要。他们三者满足的关系为：

其中a2为水面蒸发系数，L为水的潜热通量，e0和ea分别代表着饱和水压力，和气体压力，ε代表水面辐射系数，而σ代表玻尔兹曼常数。

在计算ρla2的过程中，本文总结了前苏联的经验算法，又针对本次特殊情况进行了修正，特到了以下的计算方式。

参考本文的模型:

在这里省略了风速的影响。由此我们计算并拟合出空气液体界面散热的情况（图4）。

3.4.2流体与浴缸外壁散热情况的计算

前已提及，流体在固体界面散热情况计算的具体原理，由此建立以下两个等式:

图4　浴缸各处在空气液体界面具体散热量分布

由于上下两个等式相等，我们可以计算每一个点元的Tx，从而得到每一个点元处的散热情况（图5）。

图5　浴缸各处在缸壁的散热分布曲线

4　结论

通过理论分析、研究讨论和模型建立，我们得出浴缸内部的流体温度分布情况，如图6所示。

图6　考虑散热后浴缸温度分布情况模拟

通过计算整体散热情况，对流体在复杂情况下的散热过程提供思路和方法上的探究，这将有利于对于自然界流体（岩浆，热液）、工程中使用的热水等进行温度的精确分析。

［1］Ryan P.J.，Harleman D. R. T. ，Stolzenbach K. D. ， Surface Heat Loss from Cooling Pond Water Resources Research， 1974， 10（5）

［2］Balandin A.A.， Ghosh S， Bao W. Superior thermal conductivity of single-layer graphene Nano letters， 2008， 8（3）:902-907.

［3］Lepri S， Livi R， Politi A. Thermal conduction in classical lowdimensional lattices Physics Reports，2003，377（1）:1-8

［4］Bansal N， Kimbrel T， Pruhs K. Speed scaling to manage energy and temperature Journal of the ACM （JACM），2007，54（1）:3.

［5］Soundararajan V，Zekovic S， Kovacevic R.Thermo-mechanical model with adaptive boundary conditions for friction stir welding of Al 6061 International Journal of Machine Tools and Manufacture，2005，45（14）:1577-1587.

李昂（1995-），男，汉族，吉林省长春市人，在读本科生，吉林大学地球科学学院地质学专业。

王岳（1995-），男，汉族，山东省潍坊市人，本科，吉林大学计算机科学与技术专业 。

陶然（1993-），女，汉族，辽宁省铁岭市人，本科，吉林大学经济学专业。

Foulier's Heat-Conduction Equation and Newton's Cooling Law's Mathematical Modeling Application in Fluid Thermotics

Ang Li，Yue Wang， Ran Tao
（Jilin University， Changchun， Jilin， 130021， China）

Pillar fluid's conduction of heat is of value in researching on the natural fluid.The paper is basic on a ideal model of the moving hot water in a bathtub.By using Fourier Heat-Conduction Equation and the Method of fitting， and by using the Newton's Cooling Law to optimize the process of heat-conduction， the paper transmit the three-dimensional problem into one-dimensional problem and try to discuss the process of the heat distribution and temperature balance in this model，in order to provide some mentality to the later research in fluid thermal analysis.

Fluid； Distribution of Heat； Foulier； Heat-Conduction Equation

TK11+5

A

2095-8412 （2016） 03-498-05