关于广谱哲学的交叉性学科特点

苏淼

(华北水利水电大学 马克思主义学院，河南 郑州 450046)



关于广谱哲学的交叉性学科特点

苏淼

(华北水利水电大学 马克思主义学院，河南 郑州 450046)

摘要：广谱哲学是融马克思主义哲学、系统科学和现代数学为一体的新型哲学门派，具有跨领域性、跨学科性的横断交叉学科的特点。研究广谱哲学横断交叉的机制、作用和特点，对于人们了解广谱哲学，了解一般的横断交叉学科的性质，具有重要的理论意义。

关键词：广谱哲学；交叉性；特点

广谱哲学是一个新型的交叉学科[1]，但它究竟是如何交叉的，在交叉过程中抛掉了什么？保留了什么？改造了什么？它的“新型”体现在哪里？这是许多学者关注的问题。

一、关于交叉学科的概念

交叉学科是两个或两个以上学科在某个领域内互相渗透、互相补充形成的，所以其获得的成果在两个以上的学科领域内具有贯通性、普适性。例如控制论是数学、生物学、神经生理学、无线电通讯技术、自动控制技术等学科在自动控制领域内相互渗透、相互补充的产物，所以它的成果也在上述领域具有一定的贯通性、普适性。

交叉学科的产生是因为在不同学科领域之间往往存在某个空白地带、边缘地带，它不属于或很少属于这些不同学科的专门领域，因而很少被专门的学科所涉猎。开发这个空白、边缘地带就会成为新兴学科的生长点。而这往往需要多个学科协调作战，从而使新兴学科成为交叉学科。

例如，化学是研究化学变化(相对于物理变化)的科学。其中，原子是化学变化的基本物理单位，即化学变化本质上是原子间的重新组合。因此，要深入研究各种化学变化的秘密，就要深入研究原子的结构及其内部的运动规律，而后者主要是物理学特别是量子物理学完成的。物理学和量子物理学是研究微观粒子的构造及其运动规律的科学，它并不以化学变化为研究对象，但它关于原子构造及其内部运动规律的知识却可以用来揭示化学变化的秘密。这样，在化学与物理学科(特别是量子物理)之间就出现了一个边缘地带，二者的结合就产生了一个交叉学科——量子化学(见图1)。

图1　化学与物理学的交叉

二、 广谱哲学的交叉性

广谱哲学是传统哲学、数学、系统科学等学科的交叉学科。下面分别考察它们之间的交叉情况，并用示意图给予标示。

(一)哲学与数学的交叉

哲学是各门学科中普适性最高的学科，也是学派林立、相互对立的观点杂陈的学科，如果抛掉其中达不到哲学层次的内容、抛掉唯心主义等错误内容，剩余的是带有普适性的、合理性的一般原理。例如唯物论、辩证法的基本原理。另一方面，数学也是一个庞大的学科体系，它大致上可以划分为数值型的数学和结构型的数学。前者以通常的数量及数量关系为基础，它们描述的对象是可度量、可数值化的对象。而哲学观点、哲学原理一般不可直接度量、难以数值化，因此，这部分数学对于哲学的数学化而言应该舍弃。后者(即结构型的数学)不以对象的可度量、可数值化为前提，而以扬弃了具体数量关系的抽象的关系结构为对象，包括集合论、近世代数、图论、形式语言、数理逻辑、范畴论等[2]。因此，结构型数学适合哲学问题的数学化。

传统哲学中不科学的内容(包括唯心主义的内容)、不具有最高普适性的内容被舍弃，而具有科学性、最高普适性的内容被保留(见阴影部分)。数学中以数量关系为对象的大部分数学被舍弃，而以抽象的关系结构为对象的内容被保留(见阴影部分)。因此，交叉部分(阴影部分)的内容是具有最高普适性的哲学概念、原理等与同样具有最高普适性的数学工具的结合(见图2)。

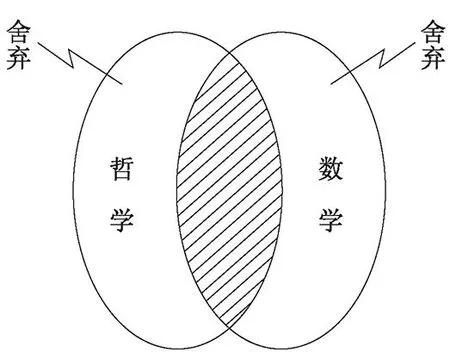
图2　哲学与数学的交叉

(二)哲学与系统科学的交叉

系统科学本身可以看成横断交叉学科，但和哲学的普适性相比，它的许多概念带有明显的具体自然科学(特别是热力学和统计物理学)的痕迹。例如：自组织理论中的熵的概念及其度量、申农信息论中的信息的概念及其度量等。

系统科学的概念要能应用于哲学问题，必须做进一步的抽象、概括。此外，它的许多带有明显具体科学技术特点的方法(如系统优化方法、信息反馈方法、功能模拟方法)也必须经过抽象、概括才能与哲学层次的方法相容(见图3)。

图3　哲学与系统科学的交叉

图3与图2类似，左侧哲学要舍弃那些非科学的、不具有最高普适性的内容，右侧系统科学要舍弃不具有最高普适性的概念和方法(如数学方法)，因此，图中阴影部分是具有最高普适性的哲学概念、原理与系统科学中具有最高普适性的概念、原理的结合。

(三)系统科学与数学的交叉

系统科学是充分运用了数学工具的横断科学，但从哲学的角度看，系统科学存在一个极不协调的状况，即一方面它的许多基本概念(如系统性、整体性、相关性、演化性等)具有极大的普适性，另一方面，它们所使用的数学工具却是数量型的数学(如线性微分方程、非线性微分方程、随机微分方程等)，这些数学要求对象可度量、可数值化。但对任意系统、任意系统的整体性、相关性、演化性，不一定可以用通常的数量关系描述(甚至由于变量和方程过多，描述了也无法处理)。这无异于“把硕大的花朵(普适性极高的概念)插到了极其纤细的茎上(数量型的数学)”。显然，要用数学来描述系统科学的基本概念和原理，只能采用数学中的另外一部分，即结构型的数学[3]194-205。

图4与图3类似，左侧的系统科学要舍弃不具有最高普适性的概念和方法，右侧的数学要舍弃以数量关系为对象的数学内容，只保留以抽象集合上的关系结构为对象的数学内容。因此，交叉部分(阴影部分)的内容是具有最高普适性的系统科学概念、原理与其具有相应相称的科学方法的结合(见图4)。

图4　数学与系统科学的交叉

三、广谱哲学的特点

上文分别阐述了广谱哲学作为三类学科交叉的具体情况，这些特殊的交叉，使广谱哲学具有了与普通交叉学科不同的特点。

第一，哲学概念的结构化。由于使用结构型的数学刻画哲学问题，因此，广谱哲学要求哲学的概念、原理必须有结构量的特征，而结构量是一种抽象的关系及其组合。因此，从传统哲学的概念中抽象出形式具体的关系结构并用结构型数学加以描述，就成为建立广谱哲学的基本工作。在广谱哲学的概念体系中，每个概念都有自己明确的关系结构，而这些关系结构又和一定的结构量相耦合，使哲学概念和数学结构有机地联系在一起，这是它的一个鲜明的特点[4]。

例如：

客观存在→n重观控下的等价性→最大变换群

量变→同类变→同一个等价类内的变化

质变→异类变→不同等价类之间的变化

矛盾的转化→阴阳主序方的转化→

反序自同构(态)

第二，数学结构的辩证化。结构型的数学作为纯数学是各种静态结构，它不考虑随时间的流变，不考虑客观事物结构的产生、发展和消亡。但唯物辩证法则重点考虑这一方面。因此，在把结构型数学应用于描述唯物辩证法问题时，涉及到对结构型数学的变革和改造。例如，结构型数学研究代数结构的“共时态”的异同关系，哲学则不仅研究任意客观结构的共时态的异同关系，还需研究任意客观事物结构的历时态的异同关系。因此，代数的结构要转换成任意结构，同时在任意结构中要引入真实的时间变量。于是在广谱哲学中，代数结构的同构、同态概念被改造成任意客观结构的动态自同构、动态自同态，使这些数学概念能够确切地刻画辩证命题。同样，等价关系的概念被改造成动态自等价。这时，事物的量变就成为在同一个自等价内的变化，事物的质变就成为事物从一个自等价类向另一个自等价类的变化。而事物“向对立面的转化”就成为“反序自同构”或“反序自同态”。

第三，系统科学模型的普适化。系统科学模型大部分为普通数量关系模型，与系统概念的普适性相比，相差甚远。系统科学与数学交叉，实质上是为系统科学的普适概念和原理建立结构型的数学模型，使二者相应相称，从而使系统科学中的数学模型可适用于任意系统[5]。

一般系统论的创始人贝塔朗菲 曾用下述方程描述系统诸元素的相互联系性：

显然，这是一个极其特殊的模型，对那些不连续也无法用数量关系表示的客观事物系统是不适用的，而采用结构数学模型(例如，含时变参量的关系模型)则不仅可以描述任意系统中诸元素的相互联系性，也可模拟“整体不等于部分和”等系统科学的结论。

四、结语

广谱哲学的构建有赖于传统哲学、数学和系统科学的交叉，而这种交叉的结果分别引起了这三个学科自身的深刻变化，无论是哲学概念的结构化、数学结构的辩证化，还是系统科学模型的普适化，又都在抽象关系结构的意义上统一起来，这正是广谱哲学的基本建构思想——辩证结构主义的一种具体体现。

参考文献：

[1] 刘先琴.将哲学原理、现代数学等结合起来的新型学科：专家研讨自主创新与广谱哲学[N].光明日报，2006-08-20(2).

[2] 张玉祥.结构型数学及其在广谱分析中的应用[J].河南科学，2009(5):525-529.

[3] 张玉祥.广谱哲学浅说[M].北京：中国社会科学出版社，2014.

[4] 汪宏.探索哲学现代化之谜：关于广谱哲学的对话[J].郑州大学学报(社科版)，1998(3)：64-67.

[5] ZHANG Y X.On the Broad-spectrum Analysis of General System Theory[J].Kybernets,2009(10)：1849-1855.

(责任编辑：王兰锋)

收稿日期：2016-02-10

作者简介：苏淼(1977—)，女，河南泌阳人，华北水利水电大学马克思主义学院副教授，研究方向为马克思主义哲学与科技哲学。

中图分类号：N031

文献标识码：A

文章编号：1008—4444(2016)04—0006—03

The Features of Interdiscipline of Broad-spectrum Philosophy

SU Miao

(School of Marxism, North China University of Water Resources and Electric Power, Zhengzhou 450046, China)

Abstract:Broad-spectrum philosophy is a new type of philosophy, which inosculates Marxist philosophy, system science and modern mathematics as a whole, with a laterally interdisciplinary characteristic. It has the important theoretical significance to study laterally interdisciplinary mechanism, functions and characteristics of broad-spectrum philosophy, because it can help to understand the broad-spectrum philosophy and understand the nature of common lateral interdiscipline.

Key words:broad-spectrum philosophy; interdisciplinary; features