走向广谱哲学的两个台阶——《广谱哲学浅说》昭示的创新路径

梁中卿

(华北水利水电大学 马克思主义学院，河南 郑州 450046)



走向广谱哲学的两个台阶
——《广谱哲学浅说》昭示的创新路径

梁中卿

(华北水利水电大学 马克思主义学院，河南 郑州 450046)

摘要：对大多数读者而言，广谱哲学是深奥、晦涩而神秘的。《广谱哲学浅说》的出版，为人们揭开了笼罩在广谱哲学上的层层神秘面纱。其中，始终围绕在初学者面前的两大谜团，即哲学问题的数学化需要什么样的数学以及怎样使哲学与这种数学接轨，在《广谱哲学浅说》中得以拨云见日。它们构成了人们走向广谱哲学的两大台阶。

关键词：广谱哲学；数学基础；哲学内核；两个台阶

了解一些广谱哲学的读者都知道，理解广谱哲学的一大障碍是它的数学基础。本来，从纯数学的角度看，它的数学基础并不难，无非是集合论、近世代数、图论等称为“离散数学”的东西。但为什么即使熟悉这些数学的读者仍感到理解广谱数学很难呢？通读《广谱哲学浅说》，发现，这里有两个台阶要上。

一、从“数量型数学”到“结构型数学”

第一个台阶是广谱哲学所用的数学模块与一般事物的机理或哲理相联系，而不是与单纯的数量关系相联系。这里的“数学模块”是指离散数学的基本概念、基本运算、基本方法等。简单地说，广谱哲学认为，离散数学的基本模块(概念、运算、方法等)已经不限于适用数量关系，而且适用于任意事物及其关系。这是数学由“数量型数学”(以数量及其关系为研究对象)经抽象变为“结构型数学”(以抽象数学结构及其关系为研究对象)的必然结果[1]194-202。

例如，映射的概念f:A→B是由函数的概念y=f(x)抽象而来，但在函数y=f(x)中，x、y是变量(变化的数量)，f是变量x、y之间的对应关系，代表某个解析表达式(如y=kx+b,y=sinx)或其他对应的数表。而在映射f:A→B中，A、B可以是任意事物(不限于数量或变量)的集合，f是A、B中任意事物之间的对应关系。例如，A是毕业生的集合，B是工作岗位的集合，则f表示每个毕业生对应一个工作岗位，或者多个毕业生对应同一个工作岗位。特别地，若A是任意客观事物的集合，f是人的认知方式(大脑处理信息的能力)，则f(A)={f(x)/x∈A}就表示人的认知结果的集合，这便与哲学上的认识论联系起来了。这时，对满射f：A→f(A)的各种数学处理(各种限定、扩展、商化、复合、组合、变换等运算)，就可以模拟“能动反映论”的种种复杂情形[2]。

显然，仅从纯数学(所谓“数量型数学”)的角度理解映射论的读者，难以理解映射论怎么会同哲学上的认识论联系起来，并从而给出认识论以全新的面貌。

为了给哲学问题建立数学模型(所谓“广义量化模型”)，广谱哲学特别重视和挖掘了“结构型数学”的一般事物机理或哲理的意义。例如，对于熟悉集合论的读者看来，等价关系是一个最常用的、用来对数学对象分类的工具。但在广谱哲学看来，等价关系及其分类蕴含着极其普遍、深刻的哲理，不仅“类内”视为“同”、“类间”视为“异”涉及到了差异与同一的矛盾关系，而且它还是“个别与一般”“现象和本质”“可知与不可知”“可预测与不可预测”“可逆与不可逆”“量变和质量”等辩证关系的共同数学基础[3]。一个持纯数学眼光的学者绝不会想到，一个平平凡凡的等价关系及其分类概念，竟然隐藏着那么多不平凡的、深邃的哲学秘密！

二、从“结构型数学”到寻找哲学问题的结构内核

第二个台阶是哲学问题如何与“结构型数学”模块接轨。如上所述，“结构型数学”是研究抽象的数学结构及其关系的科学。这里“抽象的数学结构”与传统的数量关系没有必然的联系，它一旦从传统的数量关系中抽象出来，便具有了超出数量关系的意义，反映了一般事物的机理或哲理。问题是，虽然哲学的概念或命题一般也没有数量关系——这使它与“结构型数学”有一致性，但哲学的概念或命题要与“结构型数学”接轨，缺乏的恰恰是明晰的数学结构。例如哲学上的“物质”(广谱哲学把它推广为“客观存在”)概念：“物质是不依赖于人的意识而又能为人的意识所反映的客观实在”(列宁的定义)。它是一种什么样的数学结构？又如辩证法讲的现象和本质的辩证关系：“本质决定现象，现象反映本质”，又是一种什么样的数学结构？

广谱哲学认为，一个概念或命题尽管表述可能有多种，但总有一个稳定的结构内核，这个内核不因语境的改变而改变。此内核决定了甲概念不是乙概念，此命题不是彼命题。要想让哲学的概念或命题与“结构型数学”的抽象结构相接轨，关键是找出哲学概念或命题背后的、稳定的结构内核。这就是广谱哲学的结构分析方法。

仍以“物质”(或“客观存在”)概念为例。仿照列宁的物质定义，我们可以把“客观存在”的概念定义为：“不依赖于人的意识而又能够为人的意识所反映的任何事物”。显然，关键是两个定语：“能够为人的意识所反映”和“不依赖于人的意识”。“能够为人的意识所反映”其实是说，对指定的某个对象事物a，存在着人的某个反映过程或反映方式，把对象a映入人脑，形成人脑中的某个(广义)影像。例如一个杯子a，我怎么知道它存在呢？要通过我的眼睛去看(“观”)或者通过我的手去摸(“控”)，反映到我的脑中，形成杯子的影像。当然，对象事物不一定是自然界的实物，可以是任意对象，如社会事物、社会事件、事物的发展过程等。反映方式也不限于“看”或“摸”，而是广义的观控方式。同样，人脑中的影像也是广义的，如认知结果、逻辑推论等。这样，定语“能够为人的意识所反映”就变成如下的结构：

设A是对象事物集，对于a∈A，存在一个观控方式f:A→f(A),使得f(a)∈f(A)。

再来看定语“不依赖于人的意识”。对于我面前的杯子a，我用眼睛去看(“观”)或用手去摸(“控”)，我感知到了杯子的存在：它是圆柱形的、不锈钢的、白颜色的，等等。但怎么知道这不是我的错觉呢？怎么证明我的这些结论不会因人而易呢？一个办法就是任何人或任何次的“看”或“摸”，结果是一致的，即它都是圆柱形的、不锈钢的、白颜色的，等等。这些性状不随人数或次数的多少改变而改变，这就叫“不依赖于人的意识”。其中，所谓“结果一致”，换成数学的语言，就是落到同一个等价类内。于是“不依赖于人的意识”就成为如下的结构：

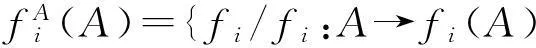
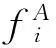
与上述结构分析类似的，辩证法关于现象和本质关系的数学模型，是一个同态映像结构[4]。限于篇幅，不再赘述。

上述例子表明，寻找哲学问题的结构内核不是轻而易举的事。它至少需要两方面的素养。一是对“结构型数学”的模块了如指掌，并且深刻地了解“结构型数学”模块的哲理意义，从而当某个哲理与某个数学模块有相近的意义时，可以考虑“接轨”。二是对哲学原理要有深刻的理解，能够做到用多套“等效”(数学上即等价)的语言置换该哲学概念或命题时，语义不变，从而可以把某个“等效”的语言与某个数学结构联系起来。可见，这确实是一个很大的台阶。

三、结语

要了解并接受广谱哲学，需要越过两个障碍或两个台阶：一是从普通数学概念——以数量关系为研究对象的“数量型数学”到以抽象的数学结构及其关系为研究对象的“结构型数学”的跨越；二是如何运用结构分析法，抽取哲学问题内含的稳定的结构内核，以便于与“结构型的数学”模块接轨。本文在《广谱哲学浅说》的基础上，展示了跨越这两大台阶的路径。这对于初学者具有一定的启示作用。

参考文献：

[1] 张玉祥.广谱哲学浅说[M].北京:中国社会科学出版社,2014.

[2] 张玉祥.结构型数学及其在广谱分析中的应用[J].河南科学,2009(5):525-529.

[3] 郭少磊.变换群与若干哲学范畴的广谱分析[J].河南科技大学学报(社科版), 2013(6):84-87.

[4] 王晓岗.关于哲学数学的一些思考:从广谱哲学谈起[J].广西社会科学,2012(9):32-35.

(责任编辑：李翔)

收稿日期：2016-04-02

作者简介：梁中卿(1979—)，男，河南商丘人，华北水利水电大学马克思主义学院研究生，研究方向为马克思主义基本原理。

中图分类号：B089

文献标识码：A

文章编号：1008—4444(2016)04—0009—02

Two Important Steps to Broad-spectrum Philosophy—Enlightenments fromAnElementaryIntroductiontoBroad-spectrumPhilosophy

LIANG Zhongqing

(School of Marxism, North China University of Water Resources and Electric Power, Zhengzhou 450046, China)

Abstract:Broad-spectrum philosophy is abstract and enigmatic to most readers. An Elementary Introduction to Broad-spectrum Philosophy which has been published reveals the great deal of the secrets of the subject. There are two puzzles confusing the learners all the time, that is, what kind of mathematics the mathematicization of the philosophical issues needs and how to make the connection between the philosophy and this kind of mathematics. They are explained in a concise mathematical language in that book. They become the two steps to broad-spectrum philosophy.

Key words:broad-spectrum philosophy; mathematical basis; philosophy connotation; two steps