大跨度斜拉桥模态参数识别时频方法对比研究

茅建校, 王　浩, 荀智翔

(东南大学 混凝土及预应力混凝土结构教育部重点实验室， 江苏 南京 210096)



大跨度斜拉桥模态参数识别时频方法对比研究

茅建校, 王浩, 荀智翔

(东南大学 混凝土及预应力混凝土结构教育部重点实验室， 江苏 南京 210096)

摘要：利用苏通大桥结构健康监测系统(SHMS)记录的台风期间大桥加速度响应，分别基于希尔伯特-黄变换(HHT)和小波变换(WT)方法对该桥进行了模态参数识别，并将2种识别结果进行对比.在此基础上，进一步研究了模态阻尼比与桥址区实测平均风速的关系.结果表明：基于HHT和WT方法识别出的模态频率值基本一致；模态阻尼比差距较大，基于HHT方法识别的阻尼比均值略大于基于WT方法的识别结果；基于HHT和WT方法识别的模态阻尼比随风速的变化趋势类似.

关键词：苏通大桥； 模态参数识别； 希尔伯特-黄变换(HHT)； 小波变换(WT)

大跨桥梁的模态参数包括频率、振型及阻尼比，它们具有明确的物理意义，是对结构进行有限元模型修正、损伤识别及振动控制等研究的基础和前提[1].环境激励法是进行大跨度桥梁模态参数识别最常用的激励方法，具有无需激振器、节省费用、安全性好等优点[2].

传统的环境激励下结构模态参数识别方法主要包括时域分析法和频域分析法[3-4].峰值拾取(PP)法和频域分解(FDD)法均是较为常用的频域分析方法，仅需在频域内对结构振动信号进行分析.PP法简单易用，但存在功率谱泄露、密集模态易丢失等问题；FDD法提升了密频结构模态参数识别的效果，但功率谱值泄露、峰值点选取主观性大等问题仍难以解决[5].随机子空间(SSI)法和自然激励(NExT)法为时域分析中较为常用的方法，2种方法在时域内直接对结构振动响应进行分析，避免了傅立叶变换造成的功率谱值泄露，但是噪声污染和虚假模态仍是阻碍其进一步发展的主要问题[6].可以发现，上述传统模态参数识别方法有一个共同的特点，即只能单独在频域或者时域进行识别，从而使识别精度受到限制.

近些年，以希尔伯特-黄变换(HHT)和小波变换(WT)为代表的时频域分析方法引起了研究人员的关注.这类方法凭借较高的识别精度和良好的抗噪能力，在结构模态参数识别领域已有一些成功的应用.Yang等[7-8]率先采用HHT方法对结构参数进行了识别研究，并提出了结构自振频率和阻尼比的识别方法.Ruzzene等[9]将WT方法运用到土木工程结构领域并对Queensborough大桥进行了模态参数的识别，从此推动了该方法在土木工程领域的研究与应用.Kijewski等[10]探讨了WT方法的频率分辨率以及端点效应的影响因素，利用对称延拓的方法进行端点效应的抑制，并验证了该方法的有效性.Yan等[11]以Z-24桥Benchmark模型的环境振动测试为例，对比分析了HHT和WT方法进行模态参数识别的能力.但是，基于HHT和WT方法，在超大跨度斜拉桥上进行的强台风期间模态参数演变特性研究仍处于起步阶段，尤其是强台风期间模态阻尼比与风速关系的模型尚未有明确定论.

针对苏通大桥结构健康监测系统(SHMS)记录的“海葵”台风期间大桥主梁跨中加速度响应，分别采用HHT和WT方法对大桥主梁模态参数进行识别，并将2种识别结果的统计特性进行对比分析.在此基础上，分析了台风期间模态阻尼比与实测风速的关系.

1　基于HHT和WT方法的模态参数识别基本原理

对于一个由白噪声激励产生的多自由度系统振动响应信号而言，可以应用随机减量(RDT)方法对其进行处理，得到相应的自由衰减响应[12].必须指出的是，这些自由衰减信号由一系列带有同样形式的衰减正弦波组成，可以记为

(1)

1.1EMD和HT方法基本原理

对于式(1)中多分量结构振动信号x(t)，利用经验模态分解(EMD)可将其分解为多个单分量的固有模态函数(IMF)及筛分余量和的形式[13]，如下所示：

(2)

式中:ci(t)为IMF;rn(t)为筛分余量，代表信号的噪声部分.

在实际应用中，往往会对振动信号做各种带通滤波处理，提高信噪比，从而使xi(t)≈ci(t)，故与xi(t)对应的解析信号zi(t)可以表示为

(3)

其中，yi(t)为xi(t)的希尔伯特变换(HT)，即

(4)

1.2WT方法基本原理

连续小波变换的实质是利用小波母函数ψ(t)与待分析信号x(t)的卷积得到一系列可以表征信号的时频分布特性的小波系数，如下所示：

(5)

式中:a>0是尺度参数;ψ*(t)是ψ(t)的复共轭函数.

基于文献[14]所述的多自由度模态解耦方法，采用WT方法进行多自由度系统的模态参数识别，可以推导出n自由度系统自由衰减信号对应的小波变换系数[10]，即

(6)

式中:b为平移参数；fc为中心频率;ft为带宽参数.

对每一阶分离的模态而言，它对应的小波系数为

(7)

1.3结构模态参数识别

如式(3)和(7)所示，HHT和WT方法均可以将多分量信号分解成单成分、类表达式的复信号，故以HHT方法为例说明模态参数的提取流程.

式(3)中的解析信号zi(t)可以进一步表示为

(8)

式中:Bi(t)为瞬时幅值，Bi(t)=Aie-2πζifit；φi(t)为瞬时相位角，φi(t)=2πfdit+θi.

在上述分析的基础上，系统第i阶频率fi和阻尼比ζi可由式(9)求得，如下所示：

(9)

综上可知，HHT和WT方法的差异主要在于复信号的提取方法不同.为进一步对比2种方法的异同点，图1给出了对应的综合识别流程图，并据此基于Matlab平台编制了相应的计算程序.

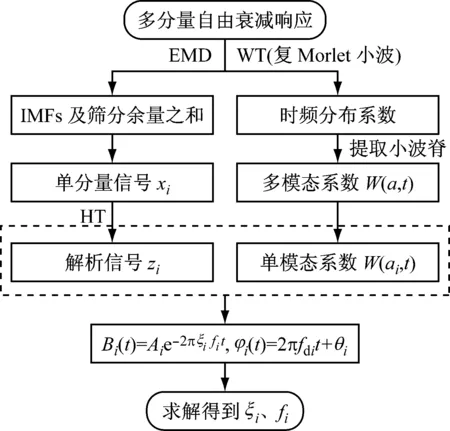
图1　基于HHT和WT方法的模态参数识别综合流程图

2　基于HHT和WT方法的苏通大桥模态参数识别及其统计特性分析

2.1基于HHT方法的模态参数识别

为初步评价HHT方法对苏通大桥主梁模态参数识别的适用性，初步选取1 h主梁跨中竖向加速度响应识别主梁模态参数，采样区间为2012年8月8日凌晨00∶00—01∶00，采样频率20 Hz，共计72 000个样本点，样本信号时程如图2所示.

图2　主梁跨中实测竖向加速度响应

首先对样本信号进行快速傅立叶变换，相应的功率谱密度(PSD)如图3a所示.由图3a可知，该PSD在0～0.7 Hz范围内存在4个峰值，即可识别出4阶模态参数.以第1阶模态参数的识别为例进行说明：利用巴特沃斯滤波器对加速度响应进行带通滤波，频率的上下限分别为0.07 Hz和0.27 Hz；随后，采用EMD方法对滤波后的加速度信号进行分解，图4为分解得到的第1阶IMF，其功率谱密度函数如图3b所示.

由图3b可知，第1阶IMF保留了样本信号的第1阶频率分量.因此，利用RDT方法过滤掉该频率分量中的强迫振动成分，从而得到对应的随机减量信号，如图5所示.其中，RDT截取阈值为1.5σ(σ为待处理信号的标准差)，自由衰减长度取为75 s，数据点数为1 500.

a样本信号b第1阶IMF

图3功率谱密度

Fig.3Power spectrum density

图4　第1阶IMF时程

图5　第1阶IMF随机减量信号

结合式(3)和(4)，对第1阶IMF随机减量信号进行HT得到对应的解析信号，根据式(8)提取对应的相位和幅值信息，并采用最小二乘法对其进行线性拟合，拟合结果如图6所示.最后，由式(9)可求得第1阶模态的自振频率为0.185 0 Hz、阻尼比为0.84%.

a幅值曲线及线性拟合b相位曲线及线性拟合

图6基于HHT方法的主梁第1阶竖弯模态参数识别

Fig.6Modal parameter identification of the first vertical mode of the girder based on HHT method

2.2基于WT方法的模态参数识别

与HHT方法不同的是，采用WT方法识别结构模态参数时直接对第2.1节中的样本信号进行随机减量预处理(截取阈值为1.5σ，自由衰减时长为102.4 s)，从而得到多分量随机减量信号.对该多分量随机减量信号进行WT，可得到反映信号能量时频分布小波系数时频分布图.在此基础上，基于模极大值理论提取了小波系数的小波脊曲线，如图7所示.其中，本文分析所采用的母小波函数以及分析得到的多分量随机减量信号和小波系数时频分布参见文献[15].

图7　小波系数脊线识别的瞬时频率

由图7可知，前80 s内各阶小波脊曲线较为平稳，而80 s以后小波脊曲线波动较大.可以表明，多分量随机减量信号各阶能量随着时间的增加衰减较大，WT方法的识别精度降低，故本文仅取前51.2 s小波脊线处的系数进行模态参数识别.

图8为主梁第1阶竖向模态对应的小波系数的幅值及相位曲线，对其进行最小二乘拟合并结合式(9)求得模态频率和阻尼比分别为0.185 5 Hz和0.56%.

a幅值曲线及线性拟合b相位曲线及线性拟合

图8基于WT方法的主梁第1阶竖弯模态参数识别

Fig.8Modal parameter identification of the first vertical mode of the girder based on WT method

2.3苏通大桥模态参数识别结果对比分析

为进一步判别所识别的模态参数的可靠性，以2012年“海葵”台风期间(8月8日00∶00—24∶00)主梁跨中截面加速度响应为研究对象，采用1 h的基本时距将其平均划分为24段，对每段加速度响应均分别采用HHT和WT方法识别相应模态参数，识别结果的统计特性如表1和2所示，其中离散系数定义为标准差与均值的比值.

如表1所示，在统计时段内，基于HHT和WT方法识别出的模态频率值与有限元计算结果均基本一致；总体而言，基于上述2种方法识别出的模态频率的离散系数均较小；对同一阶模态而言，基于上述2种方法得到的离散系数差异性较大.

表1　模态频率识别结果

由表2可知，在统计时段内，基于HHT方法的阻尼比识别结果略大于基于WT方法的识别结果.具体表现为:基于HHT方法识别的阻尼比均值介于1.65%～2.83%之间，而基于WT方法识别的阻尼比均值则处于1.09%～2.03%之间；基于HHT方法得到的阻尼比离散系数略大于基于WT方法得到的阻尼比离散系数，其中第1阶侧弯和第4阶竖弯的离散性差距最大.

对比表1和2的结果可以发现，阻尼比离散系数显著大于频率的离散性，这可能是由温度、风速和车辆等环境因素变化所致，有待进一步研究.

3　基于HHT和WT方法的模态阻尼比与风速关系模型对比分析

大跨度桥梁的主梁和风荷载之间存在一定的耦合作用，也正是这种耦合作用造成了风速与主梁模态参数尤其是阻尼比之间的关联.目前针对风速与阻尼比关系的研究还较少，两者之间的关系模型也尚未清晰[16]，因此本文利用上述基于HHT和WT方法识别的阻尼比以及桥址区实测风速研究阻尼比随风速的变化特性，其中“海葵”台风期间主梁跨中的实测平均风速如图9所示.

表2　模态阻尼比识别结果

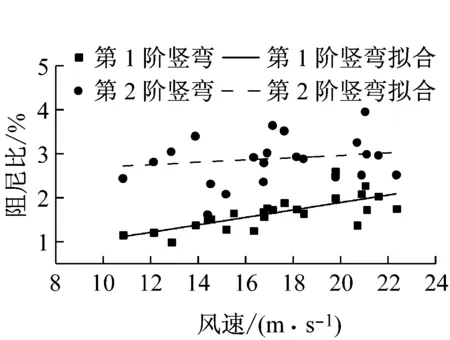
由图9可知，台风期间风速变化幅度较大，最低风速10.83 m·s-1、最高风速22.35 m·s-1.此外，台风期间，桥址区长时间降雨，温度保持在26～29 ℃之间，湿度较大但变化幅度也相对较小，从而为风速与模态参数关系的研究提供了有利条件.在此基础上，利用线性最小二乘拟合方法建立了基于HHT和WT方法识别的模态阻尼比与“海葵”台风实测平均风速的关系模型，如图10和11所示.

图9　“海葵”台风实测平均风速

a 第1、2阶竖弯模态

b 第3、4阶竖弯模态

c 侧弯及扭转模态

a 第1、2阶竖弯模态

b 第3、4阶竖弯模态

c 侧弯及扭转模态

对比图10和11可知，总体而言，基于HHT和WT方法识别的模态阻尼比随风速产生的变化趋势类似，具体表现为：对各阶竖弯模态而言，阻尼比随着风速的增大而增大；对侧弯及扭转模态而言，随着风速的增大，阻尼比先减小后增大，此时线性拟合方法无法准确描述两者的关系.

值得注意的是，本文所做研究并没有考虑风向的影响，但在海葵台风期间，实测风向变化达六十多度[17-18].与此同时，相关研究表明风向对结构阻尼比尤其是气动阻尼的影响至关重要[19].因此，在今后的研究中，有必要将风向的影响考虑在内，以对现有结论进一步完善.

4　结论

(1) 在统计时段内，基于HHT和WT方法识别出的模态频率值与有限元计算结果均基本一致，且2种方法所识别的模态频率离散系数均较小.

(2) 基于HHT方法识别的阻尼比均值略大于基于WT方法的识别结果.其中，基于HHT方法识别的阻尼比均值介于1.65%～2.83%之间，而基于WT方法识别的阻尼比均值则处于1.09%～2.03%之间.

(3) 基于HHT方法得到的阻尼比离散系数略大于基于WT方法得到的阻尼比离散系数，其中第1阶侧弯和第4阶竖弯的离散系数差距最大.

(4) 总体而言，基于HHT和WT方法识别的模态阻尼比随风速产生的变化趋势类似.具体表现为：对各阶竖弯模态而言，阻尼比随着风速的增大而增大；对侧弯及扭转模态而言，随着风速的增大，阻尼比先减小后增大，此时线性拟合方法无法准确描述两者的关系.

参考文献:

[1]Kijewski T. Full-scale measurements and system identification: a time-frequency perspective [D]. South Bend: Notre Dame, 2003.

[2]Chen J, Xu Y L, Zhang R C. Modal parameter identification of Tsing Ma suspension bridge under Typhoon Victor: EMD-HT method [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92: 805.

[3]许福友, 陈艾荣, 朱绍锋. 桥梁风洞试验模态参数识别的随机子空间方法[J]. 土木工程学报, 2007, 40(10): 67.

XU Fuyou, CHEN Airong, ZHU Shaofeng. Identification of modal parameters for bridge wind tunnel test by using a stochastic subspace technique[J]. China Civil Engineering Journal, 2007, 40(10): 67.

[4]Doebling S W, Farrar C R, Prime M B,etal. Damage identification and health monitoring of structural and mechanical systems from changes in their vibration characteristics: a literature review [R]. Los Alamos: Los Alamos National Lab, 1996.

[5]Ren W X, Zong Z H. Output-only parameter identification of civil engineering structures [J]. Structural Engineering and Mechanics， 2004, 17(3/4): 1.

[6]James G H, Came T G, Laufer J P. The Natural Excitation Technique (NExT) for modal parameter extraction from operating structures [J]. Modal Analysis, 1995, 10(14): 260.

[7]Yang J, Lei Y, Pan S,etal. System identification of linear structures based on Hilbert-Huang spectral analysis. Part 1: normal modes [J]. Earthquake Engineering and Structural Dynamics, 2003, 32(9): 1443.

[8]Yang J, Lei Y, Pan S,etal. System identification of linear structures based on Hilbert-Huang spectral analysis. Part 2: complex modes [J]. Earthquake Engineering and Structural Dynamics, 2003, 32(10): 1533.

[9]Ruzzene M, Fasana A, Garibaldi L,etal. Natural frequencies and dampings identification using wavelet transform: application to real data [J]. Mechanical Systems and Signal Processing，1997,11(2):201.

[10]Kijewski T, Kareem A. Wavelet transforms for system identification in civil engineering [J]. Computer-Aided Civil and Infrastructure Engineering, 2003, 18(5):339.

[11]Yan B, Miyamoto A. A comparative study of modal parameter identification based on wavelet and Hilbert-Huang transforms [J]. Computer-Aided Civil and Infrastructure Engineering, 2006, 21(1): 9.

[12]Asmussen J C, Brincker R, Ibrahim S R. Statistical theory of the vector random decrement technique[J]. Journal of Sound and Vibration, 1999, 226(2): 329.

[13]Huang N E, Shen Z, Long S R,etal. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London, Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903.

[14]Lardies J, Gouttebroze S. Identification of modal parameters using the wavelet transform [J]. International Journal of Mechanical Sciences, 2002, 44(11): 2263.

[15]茅建校, 王浩, 程怀宇, 等. 基于小波变换的台风激励下千米级斜拉桥模态参数识别[J]. 东南大学学报: 自然科学版, 2015, 45(1): 159.

MAO Jianxiao, WANG Hao, CHENG Huaiyu,etal. Modal parameter identification of kilometer cable-stayed bridge under typhoon excitation based on wavelet transform[J]. Journal of Southeast University:Natural Science Edition, 2015, 45(1): 159.

[16]Li H, Li S L, Ou J P,etal. Modal identification of bridges under varying environmental conditions: temperature and wind effects [J]. Structural Control & Health Monitioring, 2010, 17: 495.

[17]王浩, 程怀宇, 李爱群, 等. 台风 “海葵”作用下苏通大桥抖振全过程实测研究[J]. 桥梁建设, 2014, 44(4): 15.

WANG Hao, CHENG Huaiyu, LI Aiqun,etal. Whole-process measurement of buffeting response of Sutong Bridge under action of typhoon Haikui[J]. Bridge Construction, 2014, 44(4): 15.

[18]Wang H, Li A Q, Niu J,etal. Long-term monitoring of wind characteristics at Sutong Bridge site[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 115: 39.

[19]Zhu L D, Xu Y L, Xiang H F. Tsing Ma bridge deck under skew winds. Part Ⅱ: flutter derivatives[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(7): 807.

收稿日期：2015-08-19

基金项目：国家“九七三”重点基础研究发展计划青年科学家专题(2015CB060000)；国家自然科学基金(51378111)；教育部新世纪优秀人才支持计划(NCET-13-0128)；霍英东青年教师应用研究项目(142007)

通讯作者：王浩(1980—)，男，研究员，博士生导师，工学博士，主要研究方向为桥梁风效应及监测. E-mail:wanghao1980@seu.edu.cn

中图分类号：U448

文献标志码：A

Comparison Study on Modal Parameter Identification of Large Span Cable Stayed Bridge With Time-frequency Method

MAO Jianxiao, WANG Hao, XUN Zhixiang

(Key Laboratory of Concrete and Prestressed Concrete Structures of the Ministry of Education, Southeast University, Nanjing 210096, China)

Abstract：Acceleration responses of Sutong Bridge during typhoon Haikui were recorded by structural health monitoring system (SHMS). On the basis of recorded data, the modal parameter identification of the bridge was conducted with Hilbert-Huang transform (HHT) and wavelet transform (WT) methods, and the identified results were compared with each other. Then, the relationship between modal damping ratios and measured mean wind speed at the bridge site was studied. Results show that the identified modal frequencies based on the HHT method are almost the same with the WT-based modal frequencies. However, the difference between modal damping ratios is larger, which exhibits that the mean values of HHT-based damping ratios are larger than those WT-based results. Besides, the wind-speed-related varying trends of modal ratios identified by the HHT method are identical with those by the WT method.

Key words：Sutong Bridge; modal parameter identification; Hilbert-Huang transform (HHT); wavelet transform (WT)

第一作者： 茅建校(1990—)，男，博士生，主要研究方向为大跨度桥梁结构健康监测.E-mail:jianxiao1990@126.com