多优化目标视角下高铁站到发线运用计划编制

雷明，孟学雷

(兰州交通大学交通运输学院，甘肃 兰州 730070)



【交通运输】

多优化目标视角下高铁站到发线运用计划编制

雷明，孟学雷

(兰州交通大学交通运输学院，甘肃 兰州 730070)

摘要：在给定列车运行图和车站候车厅布局的前提下，研究高速铁路车站到发线运用问题。以股道和道岔的相容性约束作为前提，分析检票口附近固定座位数量和检票口与站台的通道距离，以增强车站作业计划稳定性、列车站内走行距离最短和最大化满足候车厅布局为3个优化目标，建立了到发线运用的0-1整数规划模型。针对模型特点，采用Lingo编程进行求解，最后通过某客运站为例证明该模型的有效性。结果表明，该模型能准确描述实际问题，适用于大型高铁站的股道分配问题。

关键词：高铁站；到发线运用；0-1整数规划；走行距离；稳定性

高速铁路车站到发线运用计划包括为列车分配到发线和安排合适的接发车进路，到发线运用优化是一类综合优化问题。贾文峥等[1]将股道分配问题(track allocation problem，TAP)的约束分为软约束和硬约束，建立了CP模型，采取含有冲突识别、值排序和Backtracking搜索3个步骤的算法对问题求解。Kroon等[2]指出车站作业计划可归结为集合配置问题(set packing problem) ，并证明当列车有3 条可选路径时，车站作业计划将成为NP-Complete问题。史峰等[3]选取到发线运用效用最大化和列车等级权重最大化为双层优化目标，建立了0-1规划模型，在Kroon等[2]算法的基础上提出了极大列车进路方案及其k剔除领域系概念，进而设计了模拟退火算法进行问题的求解。陈彦等[4]在史峰等[3]优化模型的基础上，调整了优化目标，以文献[3]的算法为基础，使用了改进的模拟退火算法进行模型求解。张英贵等[5]使用现代排序论，以总费用最小和股道均衡使用为目标，建立了多目标窗时排序模型，最后以人机交互会话的方式进行求解。龙建成等[6]引入衔接点和承载点的概念，以作业总晚点时间最短及各进路走行时间最短为目标，建立了车站进路选择模型，在模拟退火算法的基础上，提出了复合优化算法进行求解。乔瑞军等[7]以列车站内走行时间之和最小和到发线均衡使用为优化目标建立了到发线运用多目标模型，以协调优化的思想求解。赵金观等[8]在编组站到发线排序的基础上，建立了到发线和调机运用模型，以可行性安排为实现目标并设计了相应的启发式算法。苗建瑞等[9]从提高稳定性的角度出发，以车站资源运用最小为目标，建立了整数规划模型，采取了基于蚁群算法的求解方法。贾文峥等[10]采用Petri网技术，探讨了求解股道分配问题方法的强壮性。周妍[11]在运行图需要调整的情况下，用计算机重新编制了运行图，在此条件下进行车站径路问题与运行图协同编制的研究。曹岩等[12]采用差分算法，以运行晚点时间最小和编制高质量的运行计划为目标，建立了高速铁路列车运行调整模型。

一个良好的到发线运用计划应具有良好的稳定性，抗干扰能力强，考虑车站候车厅布局情况能得到使乘客的便利性提高的到发线运用计划。本文在站内走行消耗的总费用最小的优化目标的基础上，提出了增强车站到发线运用计划稳定性和最大化满足候车厅布局的优化目标。该方法解决了优化目标的单一性，突出了优化的全面性。

1　问题分析及符号说明

1.1高铁站到发线运用问题分析

高速铁路列车具有行车密度大、追踪间隔时间短的特点。良好的车站作业计划能增加运输组织效率，列车在车站内的作业包括为列车安排接发车进路及到发线，到发线运用计划是高铁站作业计划的重要组成部分。从进站段咽喉区进入到发线的通道称为接车进路，从到发线到达出站端咽喉区的通道称为发车进路。

列车对到发线的使用与列车运行图密不可分，运行图规定了任意一列车到达和离开某车站的时刻。当运行图给定时，车站要为所有列车安排无冲突的接发车进路和到发线。实质上，当接车进路确定后，相应的到发线也就确定了。在列车接车进路分配时，必须满足一些约束，如到发线占用的约束、进路冲突的约束等等，在满足约束的基础上考虑优化目标。首先，为列车安排站内走行距离最短的接发车进路可使铁路部门消耗的总费用最小；此外，列车在运行过程中会受到各种各样的扰动，车站作业计划的抗干扰能力是衡量车站作业计划优劣的一项指标，文中使用控制相邻两列车之间的缓冲时间来提高作业计划稳定性。候车厅布局在到发线运用的研究中极少涉及，本文以满足候车厅布局为一个新的角度来考虑第三个目标函数。分析检票口附近固定座位的数量和检票口与站台之间的通道距离，将候车厅布局与到发线使用进行结合，这样能制定满足更多目标的到发线运用计划。综上所述，客运站到发线运用问题是在满足约束条件的基础上，尽可能地满足优化目标。

1.2到发线运用模型的符号说明

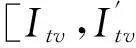
2　高铁站到发线运用模型

2.1约束条件

(1)到发线使用最小间隔时间的约束

先后占用同一股道的两列车必须满足最小时间间隔才可以确保安全。对于希望占用同一到发线d(∀d∈D)的先后两列车t和t′(t,t′∈T)，只有前一趟列车t的尾部离开股道并释放相应的道岔后，才可以对后行列车t′进行接车作业。那么两者的到达出发时间必须满足式(1)，

(1)

(2)到发线占用的约束

(3)进路冲突的约束

在车站作业中，有两项作业产生敌对进路时必须保证两项作业在使用道岔时没有冲突，也即同一道岔在同一时间段内只能有一列车占用。进路冲突如图1所示。

图1　进路冲突示意图Fig.1　Illustration of access routes conflict

在3股道的列车从A端发车，其使用的道岔集合为{11，9，5，3}。现有一列车从A端接入I股道，其使用的道岔集合为{1，5，9}，在道岔9的使用上有冲突。

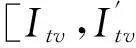
(4)接发车进路与到发线关联约束

当某列车的接车进路确定后，其相应的道岔、到发线及发车进路也就确定下来，两者之间存在关联的逻辑约束，记wtr表示列车t(∀t∈T)使用接车进路r(∀r∈R)的0-1变量，若使用为1，否则为0；wtq表示列车t(∀t∈T)使用发车进路r(∀q∈Q)的0-1变量，若使用为1，否则为0。

2.2到发线运用目标函数

(1)列车在站内走行距离最少

列车选择不同的到发线，其走行的距离不一样，当选择走行距离较短的到发线时，车站的接车作业时间缩短，耗费的资源减小，铁路部门的花费也就越少。对列车t(∀t∈T)，给出t选择某条接车进路r时所需的费用为Cr。t选择某条发车进路q时所需的费用为Cq,所走的路径越短，经过的道岔越少时，Cr和Cq就越小。那么该目标函数可以用下式表示，

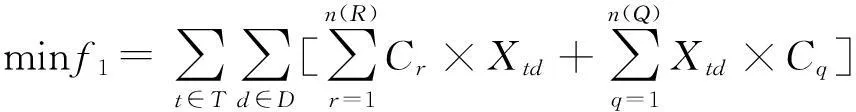
(2)

(2)到发线运用计划的稳定性

列车在运行过程中受到扰动是不可避免的，列车到发线运用计划对扰动的抵抗能力越强说明其质量越好。通过分析同一条轨道区段相邻两次占用的时间间隔是判断抗干扰能力的一个方法，时间间隔适当增加会提升抗干扰能力。到发线运用计划的稳定性对车站作业组织的稳定大有益处。

对于两列车t和t′(∀t,t′∈T)，给出ztt′表示列车t和t′是否邻接占用同一条股道的0-1变量，若t′为第一个与t列车有邻接占用关系的列车时，ztt′为0，否则为1。在满足第一个目标的基础上，两列车缓冲时间适当增大会提高车站作业计划的稳定性，增强其抗干扰能力。定义一个分段函数g(ztt′,σtt′)，σtt′表示两列车到达时间的差值即σtt′=at′-at。列车在高速铁路车站的技术作业时间短，运输组织效率高，为将该目标量化，参考了文献[9]中的稳定性评价的规则，将两列车到达时间间隔以5 min为步长划分，给出g(ztt′,σtt′)的分段情况及目标函数。

(3)

(3)满足候车厅布局及乘客便利性

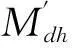
(4)

根据不同优化目标的重要程度，给出系数λ1,λ2,λ3分别代表3个不同目标函数的重要程度。将3个优化目标的重要性调查问卷分别发给铁路技术部门和调度生产部门，然后收回汇总，根据问卷结果确定λ1,λ2,λ3的值。其中0<λ1,λ2,λ3<1且λ1+λ2+λ3=1。经过上面的分析后，构建该问题的0-1整数规划模型：

min Z=λ1f1+λ2f2+λ3f3，

(5)

(6)

(7)

(8)

(9)

(10)

(11)

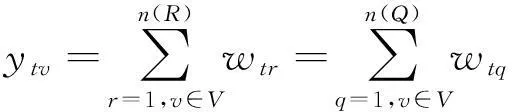
(12)

xtd,ytv,ztt′,wtr,wtq=0,1，∀t,t′∈T,∀d∈D,∀v∈V。

(13)

约束条件式(6)检验了运行图的正确性，确保列车到发时刻满足车站作业基础。式(7)是道岔占用的约束，式(8)和式(9)用来判别列车t和t′是否前后紧接续占用同一条股道，其中M为一个较大的数。约束条件(10)和(11)说明，当接车进路确定后其相应的到发线以及发车进路也就确定了。需要注意的是，当列车在某一时刻密集到达时，该模型可能存在无法为某些列车安排进路及到发线的情况，因此此处假设列车密集到达时不超过车站的接发车能力。同时加权系数λ1,λ2,λ3的确定会影响解的实用性，在结论处进行讨论。

3　算例验证

为了证明本文中提出的模型与算法的正确性，算例采用图2所示的高铁车站网络进行验算。该车站共有8条股道，4个站台，6个站台面，1、3、5、7道用于接发下行列车；2、4、6、8道用于接发上行列车。图3为该车站的候车大厅布局图，该候车大厅有4个检票口，每个检票口跟不同站台相连。检票口1、检票口2同时和站台1、站台2相连；同理检票口3、检票口4同时和站台3、站台4相连，检票口与站台相连但是走行的通道路程不同。

图2　某高铁站平面图Fig.2　2-D figure of a high-speed railway station

图3　高铁站候车厅布局Fig.3　Waiting hall layout of the high-speed railway station

根据模型定义，由于高铁站作业效率要求较高，接发列车按上下行进行区分，上行的列车只能接到上行方向的到发线，同理下行列车只能接到下行方向的到发线。

根据该高铁站旅客列车运行图，选取该高铁站9:00～15:00的42列列车的到发时刻见表1。表1中下标为奇数的列车为下行列车，下标为偶数的列车为上行列车。表1中若某列车只有出发时刻则说明该车站为始发站，同样若只有到达时刻则表明该站为终到站。

表1　9:00～15:00列车到发时刻

需要指出的是，运行图到达时刻指列车在股道上停稳后的时刻，出发时间是指列车从股道上开始移动的时刻。根据车站作业标准，列车通过车站咽喉停稳在到发线上的时间大致为2 min，同样列车从到发线出发到达另一端咽喉区的时间也大致为2 min。由于模型中的决策变量均为0-1变量，是一个LP问题。Lingo在线性规划问题的求解中表现良好，因此本问题在计算的可行性上没有问题。通过Lingo软件进行编程求解时，由于目标函数值的单位不一致，仍然采用类似建立第三个目标函数时采用的离差标准化方法进行处理。最后求解得到上述列车占用到发线顺序如图4所示。Value值为1表示占用，为0表示不占用。

根据Lingo计算得到的到发线占用的结果，还原出到发线运用方案，绘制出该车站所有停站列车的到发线运用方案，如图5所示。

从图5中可以看出，该模型为通过并在该车站停留的列车分配了无冲突的进路。由于不停站通过列车的到发时刻在运行图上一致，其在到发线运用方案图中是一个点，于是将到发线1、2分配给上下行不停站通过列车，因此到发线运用方案中不再显示1、2道。当两列车先后占用同一股道时，为了增强到发线运用方案的稳定性，两列车占用同一股道相隔时间较长；有些如t11,t15,t30等停站时间较长的列车，为减少后续停站列车的走行距离，这些列车被分配到远离正线的到发线上，增强了后续列车的稳定性及灵活性。

图4　使用Lingo程序计算的结果Fig.4　Computational results with Lingo program

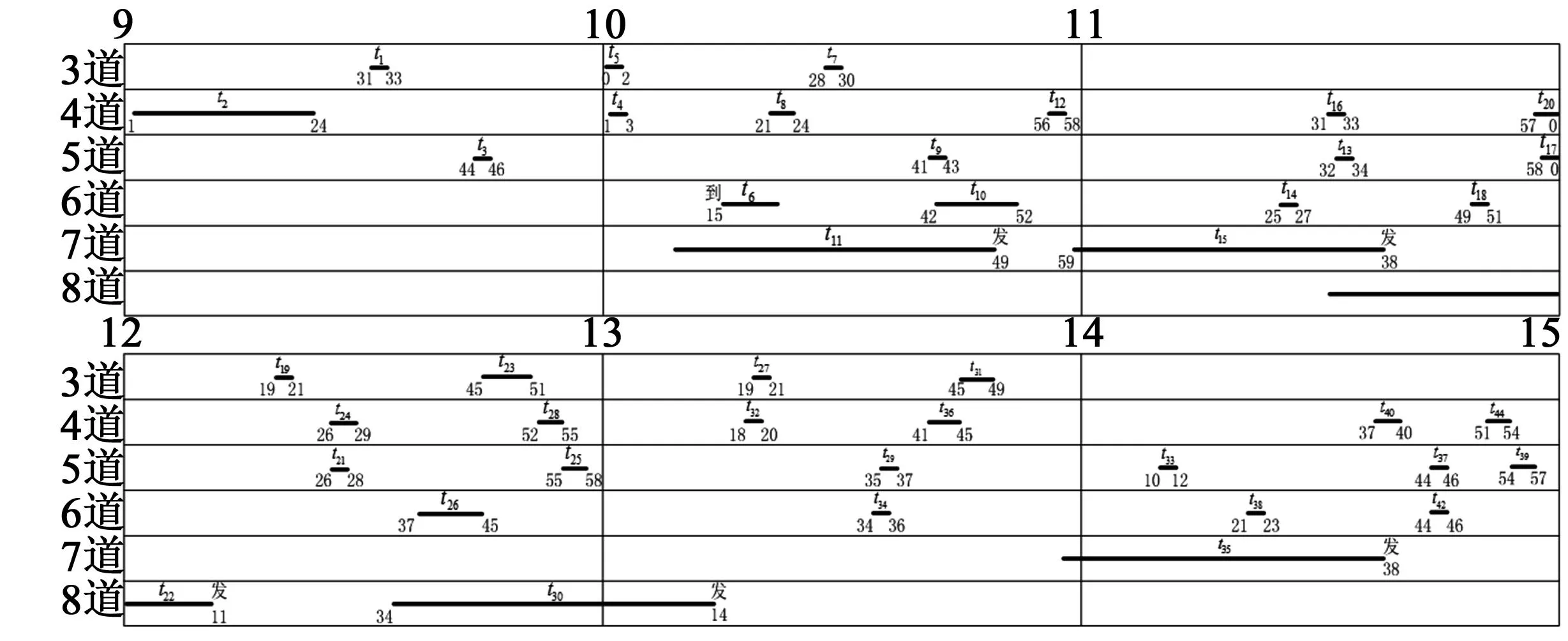
图5　到发线运用方案Fig.5　Track utilization scheme

4　研究结论

(1)候车厅布局在车站到发线运用的研究中尚未涉及，本文以候车厅布局情况为一个新的角度，同时考虑了列车走行距离最短以及车站作业计划的稳定性，为得到合理、优化的到发线运用计划奠定了基础。

(2)Lingo软件能够较快求解该到发线运用模型。通过Lingo的计算结果而还原的到发线运用方案符合实际情况，能够给该车站提供一个到发线运用方案。

(3)文中目标函数的加权系数λ1,λ2,λ3的确定非常重要，加权系数会影响到解的实用性、合理性。本文根据该车站的情况，采用调查问卷的形式对车站工作人员的意见进行搜集，确定加权系数。针对不同的车站，需要重新确定加权系数。

(4)本文研究高铁站到发线运用计划时以给定的列车运行图作为前提，但列车在区间运行时会受到各种突发事件的干扰，当干扰较大时，车站到发线使用计划需要更新。因此，如何在列车运行调整的基础上进行车站到发线运用计划的编制是下一步研究的重点。

参考文献：

[1]贾文峥,毛保华,何天健,等.大型客运站股道分配问题的模型与算法[J].铁道学报,2010,32(2):8-13.

[2]KROON L G，ROMEIJN H E，ZWANEVELD P J. Routing trains through railway stations:complexity issues[J]. European Journal of Operational Research,1997,98(3): 485-498．

[3]史峰,陈彦,秦进,等.铁路客运站到发线运用和接发车进路排列方案综合优化[ J].中国铁道科学,2009,30 (6):108-113.

[4]陈彦,史峰,秦进,等.旅客列车过站径路优化模型与算法[J].中国铁道科学,2010,31(2):101-107.

[5]张英贵,雷定猷,刘明翔.铁路车站股道运用排序模型与算法[J].中国铁道科学,2010,31(2):96-100.

[6]龙建成,高自友,马建军,等.铁路车站进路选择优化模型及求解算法的研究[J].铁道学报,2007,29(5):7-14.

[7]乔瑞军,朱晓宁,张天伟,等.客运专线车站到发线运用多目标优化模型[J].北京交通大学学报,2012,36(3):57-64.

[8]赵金观,朱志国.编组站到解作业计划自动化编制研究[J].铁道科学与工程学报,2015,12(4):962-966.

[9]苗建瑞,于勇,孟令云,等.面向稳定性的高速铁路车站作业计划优化方法[J].交通运输系统工程与信息,2012,12(3):115-121.

[10]贾文峥,毛保华,何天键,等.基于Petri网的车站股道分配方案瓶颈识别[J].交通运输系统工程与信息,2009,9(6):136-141.

[11]周妍.高速铁路列车运行图与车站径路计划协同编制理论与方法研究[D].北京：北京交通大学，2013.

[12]曹岩,孟学雷.基于改进差分算法的高速列车运行调整研究[J].铁道科学与工程学报,2014,11(6):102-108.

DOI:10.3976/j.issn.1002-4026.2016.04.013

收稿日期：2016-05-04

基金项目：国家自然科学基金(61263027)

作者简介：雷明(1992-)，男，硕士研究生，研究方向为运输组织优化。

中图分类号：U291

文献标识码：A

文章编号：1002-4026(2016)04-0060-08

Track utilization planning of high-speed railway station with multi-objective optimization

LEI Ming，MENG Xue-lei

(School of Traffic and Transportation, Lanzhou Jiaotong University, Lanzhou 730070, China)

Abstract∶We address track utilization of high-speed railway station for a definite train diagram and station hall layout. We analyze the number of ticket entrance nearby fixed seats and passage distance between ticket entrance and platform with compatible constraint of tracks and turnouts as a premise. We further construct a 0-1 integer programming model for arrival and departure track utilization with stability increase of station operational plan, shortest walk distance in a station and maximal station hall layout as optimization goals. Based on its characteristics, we solve it with Lingo programming.We eventually demonstrate its effectiveness with a high-speed railway station as an instance. Results show that it can accurately indicate practical issues, so it is suitable for track allocation issue of large high-speed railway station.

Key words∶high-speed railway station;track utilization;0-1 integer programming; walking distance; stability