数形结合提升学生思维品质

文良平

“数”与“形”的相互转化、有效结合既是数学的重要思想，更是解决问题的重要方法。如何通过“数形结合”这一重要的思想方法激活学生的思维，开阔学生的思路，使抽象问题具体化、复杂问题简单化，提升学生思维品质呢？

一、以形助数，找准数量关系

让学生先了解图形，在头脑中建立表象，再借助图形的直观性和操作实验来理清数量之间的联系，帮助学生找准数量关系，顺利解题。

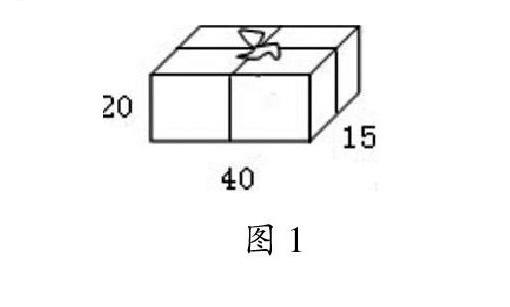
在执教人教版《数学》五年级下册《长方体和正方体的认识》时，有这样一道思考题：“一根彩带长10米，现在要捆扎一种礼盒（如图1），如果接头处的彩带长20cm，这根彩带最多可以捆扎几个这样的礼盒？”笔者先让学生猜想，最多可以捆扎几个？再让学生观察图形，分组探讨这样捆扎长、宽、高各有几条。最后，让学生亲手实验，验证猜想。最初认为长、宽、高都只有2条的部分学生发现实际上长和宽各有2条，高却有4条，围成每一个包装盒的彩带长为40×2+15×2+20×4+20=210（厘米），10米=1000厘米，1000÷210=4（个）…160（厘米）。通过仔细观察和动手实验，学生能够清晰地找出各数量关系，解起题来更加得心应手。

二、见数思形，理清公式推导过程

数学教学中一些计算公式比较抽象，推导过程比较繁琐，如果能让学生见数思形，借助直观图形解题，则有助于促进学生对计算公式的理解和建构。

笔者在执教人教版《数学》五年级上册《平行四边形的面积》时，先出示算式4×3=12（平方厘米），问学生看见这个算式后想到了什么。有学生说想到一个长是4厘米，宽是3厘米的长方形，它的面积就是12平方厘米。笔者继续追问，如果有一个底是4厘米，高是3厘米的平行四边形，它俩的面积相等吗？有的学生说相等，也有的学生摇摆不定。这时，笔者让学生拿出事先准备好的方格纸，按小组进行验证，先在方格纸上画出一个长4厘米、宽3厘米的长方形和一个底是4厘米、高是3厘米的平行四边形，让学生数一数长方形占的格数就是长方形的面积，平行四边形不像长方形这么整齐，需要把不能占满一格的按半格计算，都是12格，发现长方形的长等于平行四边形的底，长方形的宽等于平行四边形的高，也就是说长方形的面积等于平行四边形的面积。接着，笔者又拿出准备好的长方形和平行四边形的图形，让学生通过剪、拼的方法找出长方形和平行四边形的联系，学生通过操作活动，把平行四边形沿着它的一条高剪开，再拼到另一边上，拼成的长方形与原来的长方形能够完全重合，再次证明长方形的长等于平行四边形的底，长方形的宽等于平行四边形的高，长方形的面积等于平行四边形的面积。

如此通过见数思形的实验操作，让学生经历平行四边形的计算公式的推导过程，将计算公式的教学趣味化、形象化，从而帮助学生在轻松、愉快的学习氛围中理解计算公式的形成过程。

三、数形结合，化解教学难题

对于比较复杂的数学问题，可以利用数与形的有效结合，寻找解题的突破口，成功化解教学难题。

笔者在执教人教版《数学》五年级下册《分数的意义和性质》时，有这样一道练习题：“一盘草莓不足20个，分给小朋友，每人3个还剩2个，每人4个还少3个，这盘草莓是多少个？”刚开始很多学生无法动笔，有的学生认为应该求3和4的最小公倍数，剩下的2个和还少3个又不好处理，有的学生用3和4的最小公倍数12+2+3=17，为什么这样算，他自己也说不清楚，只觉得这样能同时满足两个条件。为让学生有一个清晰的认识，笔者提示学生画图分析，先在草稿纸上画两排小三角形，每排20个。再让学生根据题意依次画圈，先圈每组一个人的：上排1人3个余2个，即5个，下排1人4个少3个，即1个。再圈每组2个人的，依次类推，直到圈出的小三角形的个数一样多为止。很多学生都圈出了17个。这时，一名学生提出用列表法来表示更清晰。

教学中，渗透数形结合思想方法，可以优化数学解题的过程，提高对数学的理解能力，强化学生思维的深刻性，增强学生思维的灵活性。

（作者单位：公安县甘家厂乡中心学校）