汽车动力总成V型悬置系统的优化设计
林逢辉,李广龙
(华南理工大学 汽车工程学院,广东 广州 510641)
汽车动力总成V型悬置系统的优化设计
林逢辉,李广龙
(华南理工大学 汽车工程学院,广东 广州 510641)
以纵置式发动机的V型悬置系统为研究对象,阐述了V型悬置系统的解耦理论,推导了V型悬置组弹性中心落在扭矩轴上的条件,分析了质心坐标系与扭矩轴坐标系下计算固有频率和能量分布的方法,提出了一种V型悬置系统优化设计的方法,以固有频率、解耦率为目标,对悬置系统刚度及安装角度进行了优化,并给出了一个纵置直列四缸发动机V型悬置系统的优化案例。
纵置发动机;V型悬置;弹性中心;优化
传统内燃机汽车的振动主要由发动机引起,良好的悬置设计可以有效减少由发动机向车身和底盘传递的振动,以提高汽车的耐久性和舒适性。动力总成V型悬置系统是指动力总成发动机端与变速器端分别采用2组V型悬置支承,每组V型悬置均由2个相同的悬置呈一定角度以左右对称的形式布置。采用这种布置形式,可以实现较大的横向刚度,容易调整弹性中心,且能解除垂向、横向和侧倾自由度之间的耦合,主要应用于纵置式发动机[1]。本文分析了V型悬置系统的优化设计方法,以固有频率、解耦率为目标,对悬置系统进行优化,并给出实例。优化方法可直接应用于工程实际。
1 V型悬置的特性分析
1.1V型悬置的解耦布置
以发动机质心为原点分别建立质心坐标系OXYZ、主惯性轴坐标系OXpYpZp和扭矩轴坐标系OXtYtZt(见图1)。X轴平行于发动机曲轴轴线,并指向发动机前端,Z轴与气缸轴线平行向上,Y轴由右手定则确定;Xp、Yp和Zp轴分别为动力总成的惯性主轴。在绕曲轴的外力矩作用下,发动机将绕某一特殊轴转动,此轴即为扭矩轴Xt,扭矩轴在动力总成质心坐标系中的方向余弦为[2]:
式中,Jxx、Jyy和Jzz为动力总成的主惯性矩;αxp、βxp、χxp、αyp、βyp、χyp、αzp、βzp和χzp分别为相应惯性主轴与质心坐标系OXYZ各坐标轴的夹角。通过构造动力总成惯性矩的二阶张量,求其特征值,即得到发动机主惯性矩。通过相应的方向余弦,可求得惯性主轴与坐质心标系各坐标轴的夹角。

图1 动力总成上的不同坐标系
考虑到纵置式发动机扭矩轴与质心坐标系Y轴夹角一般接近直角,可以近似认为Y、Yt、Yp轴重合,此时扭矩轴位于质心坐标系OXZ平面上,则上式可以简化为:
cosβt=0
cosχt=-sinαt
应尽量避免发动机各自由度方向的振动耦合,否则会加剧振动。对于V型悬置系统,当悬置系统弹性中心与动力总成质心重合时,可实现六自由度解耦;但现实中往往难以实现。实际设计时,通常将前悬布置在动力总成的一阶弯曲模态的一个节点上,再根据撞击中心理论,将后悬布置在前悬置的共轭点上[3],使前后悬置的振动不相互影响。另外,考虑到常用四缸发动机的振动主要来自于垂向与绕曲轴方向,只要动力总成发动机端与变速器端2组V型悬置所在平面与扭矩轴垂直,并且2组V型悬置的弹性中心点能落在扭矩轴上,则可以实现垂向、横向和侧倾自由度的完全解耦。
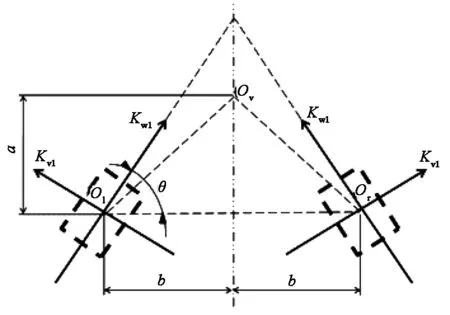
图2 V型悬置参数示意图
V型悬置参数示意图如图2所示,悬置所在平面垂直于扭矩轴,Ol、Or为左右悬置弹性中心,Ov为V型悬置组弹性中心,V型悬置组弹性中心与悬置弹性中心的垂向距离为a,横向距离的一半为b,θi为悬置安装角度,各设计参数满足下式[4]:
(1)
式中,kwi、kvi为各悬置沿图中弹性主轴方向主刚度,i=1,2分别表示发动机端和变速器端V型悬置组。
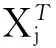
则在扭矩轴坐标系下,V型悬置组弹性中心与扭矩轴Z向的距离为:
(2)

另外,整理式1可得:
aiLitg2θi-bi(1-Li)tgθi+ai=0(i=1,2)
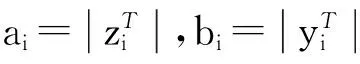
1.2V型悬置系统的振动分析
假定发动机为一刚体,建立六自由度模型,则动力总成的运动微分方程为[5]:
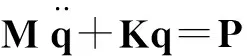

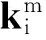

系统第j阶固有频率振动时第k个广义坐标上分配的能量所占系统总能量百分比,即解耦率为[6]:
扭矩轴坐标系下的质量阵与刚度阵分别为:Mt=RTMR,Kt=RTKR。其中,R为质心坐标系与扭矩轴坐标系转化矩阵。
与在动力总成质心坐标系下类似,可以解得扭矩轴坐标系下的固频和解耦率。
2 V型悬置系统优化方法
2.1目标函数
基于动力总成固有频率与能量分布的要求,建立目标函数:
式中,ωf、ωe、ωd为权系数;fi为各方向解耦率计算值;fd、fu分别为目标解耦率的上、下限;ei为各方向解耦率;eopt为各方向目标解耦率;d1、d2分别为扭矩轴坐标系下V型悬置组弹性中心与扭矩轴Z向的距离,可由式2求得。
2.2设计变量及约束条件
每组V型悬置均由左右2个相同悬置对称布置,悬置系统设计变量为:

式中,kui、kvi、kwi分别为悬置在局部坐标系下的三向静刚度;θi为悬置安装角度;i=1,2分别表示发动机端和变速器端V型悬置组。
为使动力总成在垂直方向与绕Y轴扭转振动方向解耦,前后悬置在垂直方向的刚度满足下式:
式中,KFZ、KRZ分别为前、后悬弹在动力总成质心坐标系下的Z向刚度;LF、LR分别为前、后悬弹性中心距质心的距离。
根据悬置的结构形式并考虑制造条件,给出悬置Z向的上下限约束与三向刚度比例约束:
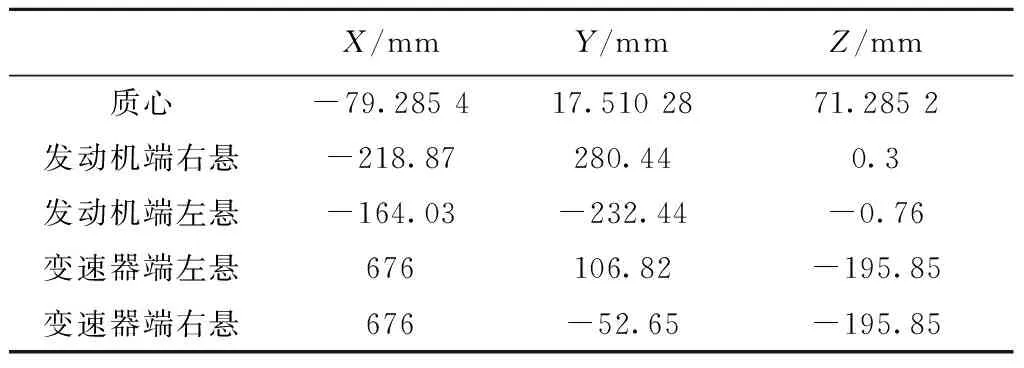
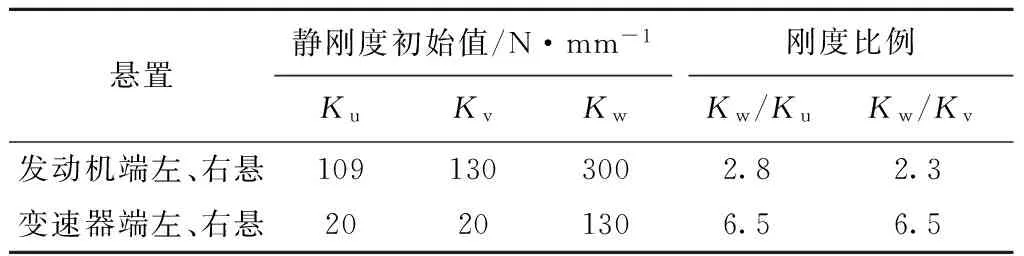
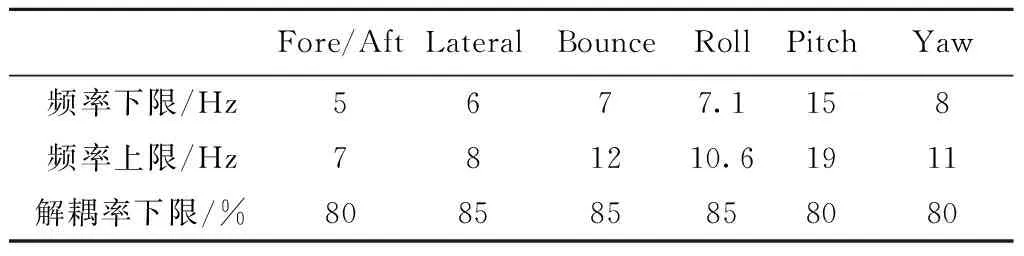
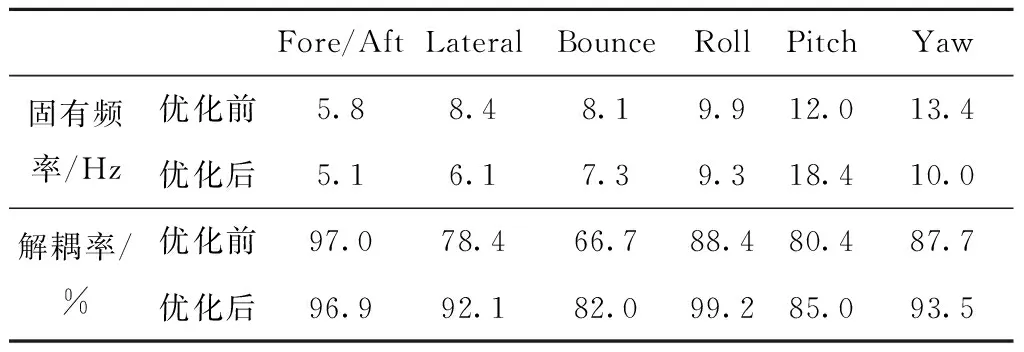
Lwi 3.1已知参数 已知一车型发动机为四缸机,发动机纵置,参数和约束条件见表1~表5。整车坐标系Z轴垂直向上,X轴水平向后,Y轴由右手定则确定。动力总成质心坐标系与整车坐标系平行。 表1 动力总成质量及在质心坐标系中转动惯量(kg·m2) 表2 动力总成质心及悬置安装点在整车坐标系中的坐标 表3 各悬置刚度初始值及刚度比例 表4 各悬置静刚度约束条件 表5 安装角度初始值及约束条件 3.2动力总成固有频率和能量分布设计 四缸机主要激励阶次为2阶,本例中的纵置四缸发动机的怠速转速为850 r/min,动力总成绕曲轴即动力总成质心坐标系绕X方向为主要激励方向,其固有频率应为850/60×(0.5~0.75)=7.1~10.6 (Hz),动力总成质心坐标系Z方向除需要避开人体垂向敏感频率(4~7 Hz)外,还应低于怠速1阶激励。动力总成质心坐标系Y方向、Z方向与绕X向为主要激励方向,这3个方向上的解耦率要求>85%,其他方向要求>80%。具体设计要求见表6。 表6 动力总成固有频率与能量分布设计要求 3.3优化设计结果 根据第3部分中给出的目标函数与约束条件,采用遗传算法,优化得到各个悬置在其局部坐标系下的静刚度及安装角度(见表7和表8)。 表7 各悬置刚度优化值及刚度比例 表8 安装角度优化值 分别计算优化前、后固有频率与解耦率分布情况,结果见表9。相比优化前,优化后的固有频率分布更为合理,解耦情况较为理想。 表9 优化前、后固有频率与能量分布对比 V型悬置系统最显著的特点是能解除动力总成横向与侧倾振动间的耦合,尤其适用于纵向布置,有较大侧倾方向激励力的动力总成,例如柴油机。本文分析了V型悬置系统的解耦布置理论,推导了使V型悬置组弹性中心落在扭矩轴上的条件,并提出了一种优化方法,以固有频率、解耦率为目标,对悬置系统进行了优化。文中给出一纵置四缸发动机悬置系统优化实例,说明了优化方法的有效性。 [1] 吕振华,范让林,冯振东.汽车动力总成隔振悬置布置的设计思想论析[J].内燃机工程,2004,25(3):37-43. [2] 上官文斌,蒋学锋.发动机悬置系统的优化设计[J].汽车工程,1992,14(2):103-110. [3] Riesing E F.Resilient mountings for passenger car powerplant[J].SAE Trans,1950(1). [4] Timpner F F.Design considerations in engine mounting[C].SAE 966B,1965. [5] 吕振华,范让林.动力总成悬置系统振动解耦设计方法[J].机械工程学报,2005,41(4):49-54. [6] 杜建国.某客车动力总成悬置系统振动解耦优化设计[J].新技术新工艺,2014(2):40-41. 责任编辑马彤 Design Methods of V-type Mounting Systems with Longitudinal Engine LIN Fenghui, LI Guanglong (College of Automotive Engineering, South China University of Technology, Guangzhou 510641, China) Present the analytical methods for the V-type mounting systems with the front longitudinal engine. Firstly, the methods of torque roll axis decoupling are described and analyzed. Then, the conditions of elastic center coincides with the torque axis are proposed and discussed. The calculation of decoupling rate and natural frequencies is carried out both in the center of mass coordinate system and torque roll axis coordinate system. Thirdly, an optimization method of V-type mounting systems is proposed to estimate the mount stiffness and orientations meeting the requirements for reasonable allocation of the natural frequencies and meeting the requirement for maximum of the modal energy distributions of the powertrain in six directions. At last, an example is given to validate the design methods for the V-type mounting systems. longitudinal engine, V-type mounting systems, elastic center, optimization methods 2016-03-29 U 464 A 林逢辉(1989-),男,硕士研究生,主要从事汽车动力学、汽车振动分析与控制等方面的研究。3 优化实例





4 结语

