基于H∞滤波的空天飞行器惯性/天文组合导航方法*

施丽娟 熊 智 王 融 殷德全 郁 丰

1.南京航空航天大学自动化学院，南京210016 2.南京航空航天大学航天学院, 南京 210016



基于H∞滤波的空天飞行器惯性/天文组合导航方法*

施丽娟1熊 智1王 融1殷德全1郁 丰2

1.南京航空航天大学自动化学院，南京210016 2.南京航空航天大学航天学院, 南京 210016

由于空天飞行器特殊的飞行任务和复杂的飞行环境，单一的导航系统难以完全独立地为其提供高精度的导航参数。天文导航作为一种完全自主的导航技术，可以提供误差不随时间积累的高精度姿态信息，与惯性导航系统组合可以提高空天飞行器长时间导航精度。同时针对复杂空天环境下，实际导航系统噪声统计特性难以精确获得而导致传统卡尔曼滤波器性能下降的问题，提出了一种基于H∞滤波的空天飞行器惯性/天文组合导航方法，建立了发射惯性系下组合导航系统的数学模型和H∞滤波模型。仿真结果表明，该方法可有效解决系统噪声建模不准确的问题，提高空天飞行器组合导航系统的精度和可靠性。 关键词 空天飞行器；组合导航；发射惯性系；H∞滤波

空天飞行器(Aerospace Vehicle，ASV)是一种集航空器、航天器和运载器于一体的可重复使用新型飞行器，其飞行包络宽广，整个飞行过程需经历起飞、加速入轨、在轨驻留、灵活变轨和高速再入5个阶段[1-3]，这种复杂的运动特性和飞行环境要求其导航系统具有跨空天、超长时间下的高可靠性和高精度工作能力[4]。

惯性导航系统具有短时精度高，可连续输出载体姿态、位置和速度等信息，以及完全自主、可靠等优点，必将成为未来空天飞行器导航系统的重要信息单元。但惯性导航系统导航误差随时间不断积累，单纯地依靠惯性导航无法满足空天飞行器长距离长时间导航需求[5-6]。天文导航系统是一种完全自主的导航技术，隐蔽性好，定姿精度高，且测量误差不随时间而积累，采用天文导航辅助惯性导航的惯性/天文组合导航具有完全自主和抗电磁干扰能力强等优点，在空天飞行器的导航领域具有良好的应用前景[4,7-8]。

传统的航空飞行器以地理系为参考坐标系，在捷联惯性导航系统算法编排中对重力场、曲率半径变化等采用直接忽略或简化处理[9]。而空天飞行器既需要在大气层内作高超声速巡航飞行，又要穿过大气层进入轨道运行，其飞行高度高，飞行时间长，飞行距离远，地球重力、曲率半径等变化较大，这些因素如果在空天飞行器飞行中忽略或简化处理，将会在很大程度上影响导航精度。此外，空天飞行器复杂的飞行环境可能导致组合导航系统很难对所有测量过程实现精确的建模，噪声统计特性也难以精确获得，因此采用传统的基于高斯分布的卡尔曼滤波器，其实际导航性能将受到限制[10-11]。

发射惯性系是以发射点作为原点的惯性坐标系，满足牛顿力学规律，其相对于地心惯性系保持不变[12-13]。采用基于发射惯性系的惯性导航系统编排方法，充分考虑地球非理想球形的因素，可以有效克服地理系算法编排的不足。H∞滤波是一种鲁棒滤波算法，对系统噪声等建模的不准确和干扰具有较好的抑制作用[14-16]。因此，本文结合空天飞行器跨空天飞行特性，提出了一种发射惯性系下基于H∞滤波的惯性/天文组合导航方法，以满足空天飞行器高精度导航任务需求。

1 基于H∞滤波的发射惯性系下惯性/天文组合导航算法

1.1 发射惯性系下捷联惯性导航算法编排

发射惯性坐标系OlXlYlZl定义为：原点Ol为发射点；OlXl轴位于发射点的水平面内，通过发射点指向发射方向；OlYl轴为过发射点的垂线，向上为正；OlZl与OlXl，OlYl构成右手坐标系，发射惯性坐标系坐标轴相对于惯性空间静止，不随地球而转动[13]。

载体坐标系ObXbYbZb定义为前上右坐标系。

发射惯性系下，根据四元数微分方程，载体姿态解算模型为：

(1)

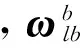
发射惯性系下，载体速度解算模型为：

(2)

式中，fb为加速度计比例输出，G为地球万有引力模型，可采用如下表达式[17]

(3)式中， (x,y,z)为载体在地心惯性坐标系中的位置，J2为引力场二阶带谐项系数，取值为J2=1.08263×10-3，相比于传统以地理系为导航系的捷联惯导算法中对重力模型的简化，上式采用引力位函数，充分考虑了地球非理想球形的影响，比传统地理系模型精度更高，更适用于空天飞行器跨空天飞行。

在发射惯性系下，载体位置解算模型为：

(4)

陀螺和加速度计的测量模型如下：

(5)

式中，ωr为陀螺随机游走误差，ωε为陀螺测量白噪声，fr为加速度计随机游走误差，ωn和fn分别为陀螺和加速度计随机游走驱动白噪声。

1.2 基于H∞滤波的发射系下惯性/天文组合导航系统数学模型

结合1.1节所述发射惯性系下捷联惯导算法，推导发射惯性系下状态方程和量测方程，考虑到空天飞行器复杂飞行环境下无法获取精确的系统噪声模型，而传统卡尔曼滤波器不再适用，因此构建基于鲁棒原理的H∞滤波器。

1.2.1 发射系下惯性/天文组合导航系统方程

根据式(1)，(2)，(4)和(5)，可以建立发射惯性系下导航系统误差增量方程如下：

(6)

选择式(6)中9维导航误差和6维惯性器件误差为系统状态变量，则组合导航系统状态方程为：

(7)

其中，状态变量为

X=[δq1δq2δq3δpxδpyδpzδvxδvy
δvzωrxωryωrzfrxfryfrz]

(8)

系统白噪声矢量为

W=
[ωεxωεyωεzωnxωnyωnzfnxfnyfnz]T

(9)

对于惯性/天文组合导航系统观测方程，对姿态误差的四元数矢量部分进行观测，有：

Zs(t)=δq13+qη,13=Hs(t)X(t)+NS(t)

(10)

1.2.2 离散型H∞滤波器构建

H∞滤波器是鲁棒滤波的典型代表，将博弈论思想应用在系统状态估计中，对实际系统中存在的系统模型误差和不确定噪声具有鲁棒性[17-20]。离散型H∞滤波可表述为：

1)离散化系统方程，被估计量

(11)

其中，Wk和Vk为噪声项，其可能是确定性噪声，也可能是统计特性未知的随机噪声。状态变量的线性组合Zk为被估计量，若想直接估计状态量，则设置Lk=I。

2)代价函数

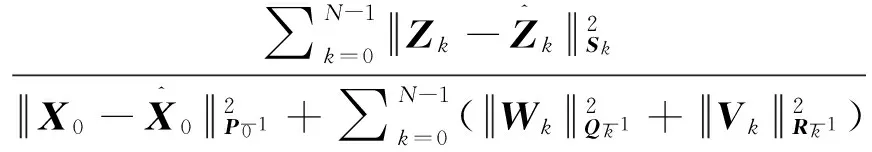
(12)

式中，θ为预先选定的H∞滤波器性能上界，称为H∞滤波器的鲁棒因子。P0,Qk,Rk,Sk为针对具体问题设定的正定对称矩阵，分别为初始估计误差协方差阵、系统噪声协方差阵、量测噪声协方差阵和状态变量线性组合估计误差协方差阵。H∞滤波的博弈论思想是在P0,Qk,Rk达到上界时，寻求估计策略使J1达到最小，即在干扰极大化的情况下使估计误差最小化。

3)求解步骤

(13)

由式(13)可以看出，当鲁棒因子θ=0时，H∞滤波模型和传统卡尔曼滤波模型是一致的，调节鲁棒因子θ改变H∞滤波的鲁棒性能。

4)限制条件

在H∞滤波估计过程中，需满足

(14)

否则H∞滤波器不存在。

2 惯性/天文组合导航系统仿真验证

2.1 仿真条件设置

选择空天飞行器发射段为研究对象，飞行器发射初始经度、纬度、高度为：118°E，32°N，100m，发射时间为2015年1月15日0时0分0秒，发射方位角为30°，飞行时间为900s。飞行航迹如图1所示。

图1 发射系下三维航迹示意图

在仿真中，设置导航传感器仿真参数如表1所示。

表1 发射系下三维航迹示意图

H∞滤波器参数设置如下：

1)初始状态：

(15)

2)初始协方差：

(16)

3)系统噪声方差：

(17)

4)量测噪声方差：

(18)

5)鲁棒因子

(19)

传统卡尔曼滤波器只需要设置前面4个参数，其值大小和H∞滤波器参数设置一致。

从表1中可发现，仿真条件1下，实际系统模型参数和滤波器中的模型参数一致，即该仿真条件下系统模型准确已知；仿真条件2下，实际系统模型中陀螺误差参数和滤波器中的误差参数并不一致，此仿真条件下可认为模型存在建模误差。

2.2 算法仿真分析

针对本文提出的基于发射惯性坐标系的空天飞行器捷联惯性导航算法以及惯性/天文组合导航H∞滤波算法，借助MATLAB进行算法的仿真验证。

1)发射系下纯惯导仿真

基于仿真条件1，进行发射惯性系下纯惯性导航系统性能测试。图2为纯惯性导航误差曲线。由仿真结果可以看出，发射惯性系下捷联惯导解算误差会随时间积累而不断增大，无法独立提供高精度的导航参数信息。

2)惯性/天文组合导航仿真

基于表1的2种仿真条件，分别进行惯性/天文组合导航H∞滤波器仿真测试，并与相同条件下的卡尔曼滤波进行比较。其中，图3为仿真条件1下的导航误差曲线，图4为仿真条件2下的导航误差曲线，表2为组合导航性能RMS统计结果。

图2 发射系下纯惯导误差曲线

图3 仿真条件1下组合导航误差曲线

图4 仿真条件2下组合导航误差曲线

图3和4中的图标KF表示采用卡尔曼滤波器，HF表示采用H∞滤波器。从图3(a)姿态误差对比曲线可以看出，在仿真条件1下，即实际系统模型参数和滤波模型参数一致时，惯性/天文组合导航系统采用传统卡尔曼滤波性能稳定可靠，精度较纯，惯导显著提高，且H∞滤波效果和卡尔曼滤波效果基本相同；观察图4(a)仿真条件2下姿态误差对比曲线，发现当系统存在建模误差时，采用传统卡尔曼滤波时姿态误差呈现较大的偏移，而H∞滤波通过调节鲁棒因子可以使其稳定可靠工作，对应姿态误差曲线呈现较稳定的状态。同样从表2的统计结果可以得到，当实际系统模型与滤波模型存在差异时，采用H∞滤波较传统卡尔曼滤波姿态精度提高20%左右。需要注意的是，图3和4中虽然惯性/天文组合导航位置误差和速度误差较纯惯导明显减小，但仍呈现发散的趋势，这是因为惯性/天文组合导航是姿态组合，对位置和速度的修正作用有限。

表2 惯性/天文组合导航性能统计(RMS统计)

3 结论

针对空天飞行器跨空天长时间飞行的特性，及对导航系统可靠性和精度的要求，提出了一种基于发射惯性坐标系的空天飞行器惯性/天文组合导航方法。针对系统噪声统计特性不准确，传统卡尔曼滤波器性能下降的问题，构建了基于博弈论思想的H∞滤波模型。仿真结果表明，在系统误差模型准确的情况下，H∞滤波性能和传统卡尔曼滤波性能相当；而在系统误差模型不准确的情况下，H∞滤波器性能优于传统卡尔曼滤波器，更适应于空天飞行器复杂的飞行环境，为进一步的空天飞行器导航系统研究提供了参考。

[1] Ding J, Balakrishnan S N. Intelligent Constrained Optimal Control of Aerospace Vehicles with Model Uncertainties [J]. Journal of Guidance, Control, and Dynamics, 2012, 35(5): 1582-1592.

[2] Chao T, Wang S Y, Yang M. Integrated Modeling, Design and Simulation Platform for Aerospace Vehicle Entry Guidance and Control[J]. Journal of System Simulation, 2011, 23(1): 47-50.

[3] 宋博, 李高峰. 美国X-37B轨道试验飞行器的发展及分析[J].飞航导弹, 2012，(12):3-9. (Song Bo, Li Gaofeng. Development and Analysis of the X-37B track Test Vehicle of the United States[J].Aerodynamic Missile Journal, 2012，(12):3-9.)

[4] Yang S J, Yang G L, Shan Y D, et al. SINS/CNS Tightly Integrated Navigation Algorithm for Aerospace Vehicles[J]. Journal of Chinese Inertial Technology, 2013, 21(4):478-483.

[5] Creamer G. Spacecraft Attitude Determination Using Gyros and Quaternion Measurements[J]. Journal of the Astronautical Sciences, 1996, 44(3): 357-371.

[6] 秦永元. 惯性导航[M]. 西安: 科学出版社, 2006.(Qin Yongyuan. Inertial Navigation[M]. Xi’an: Science Press, 2006.)

[7] 张承. 空天飞行器惯性/天文组合导航技术研究[D].南京:南京航空航天大学,2012.(Zhang Cheng. Research on SINS/CNS Integrated Navigation Technique of Aerospace Vehicle [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012.)

[8] 陈海明, 熊智, 乔黎,等.天文-惯性组合导航技术在高空飞行器中的应用[J].传感器与微系统, 2008, 27(9):4-6.(Chen Haiming, Xiong Zhi, Qiao li, et al. Application of CNS/INS Integrated Navigation Technology in High-altitude Aircraft [J]. Transducer and Microsystem Technologies, 2008, 27(9):4-6.)

[9] 刘建业,曾庆化,赵伟,熊智,等. 导航系统理论与应用[M]. 西安:西北工业大学出版社,2010.(Liu Jian-ye, Zeng Qinghua, Zhao Wei, et al. Theory and Application of Navigation System [M]. Xi’an: Northwestern Polytechnical University Press, 2010.)

[10] Kalman R E. A New Approach to Linear Filtering and Prediction Problems [J]. Journal of Basic Engineering, 1960, 82(1): 35-45.

[11] 秦永元.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社, 1998.(Qin Yongyuan. Principles of Kalman Filter and Integrated Navigation[M]. Xi’an: Northwestern Polytechnical University Press, 1998.)

[12] 潘加亮, 熊智, 王丽娜,等. 一种简化的发射系下SINS/GPS/CNS组合导航系统无迹卡尔曼滤波算法[J]. 兵工学报, 2015, 36(3):484-491.(Pan Jialiang, Xiong Zhi, Wang Lina, et al. A Simplified UKF Algorithm for SINS /GPS /CNS Integrated Navigation System in Launch Inertial Coordinate System[J]. Acta Armamentarii, 2015, 36(3):484-491.)

[13] 刘朝山. 弹载星敏感器原理及系统应用[M]. 北京:国防工业出版社, 2011.(Liu Chaoshan. Principle and Application of Star Sensor of Missile Borine[M]. Beijing: National Defense Industry Press, 2011.)

[14] 郝燕玲, 刘志平. 卡尔曼滤波与H∞滤波在GFSINS中的对比[J]. 华中科技大学学报(自然科学版), 2010,(5):19-23.(Hao Yanling, Liu Zhiping. Comparison of Kalman Filtering with H∞Filtering in GFSINS[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2010,(5):19-23.)

[15] 魏伟, 秦永元, 张晓冬,等. H∞滤波在惯导/GPS组合导航应用的比较分析[J]. 西安工业大学学报, 2012, 32(11):874-885.(Wei Wei, Qin Yongyuan, Zhang Xiaodong，et al. Comparatice Analysis of H-infinity Filtering in INS/GPS Integrated Navigation Application[J]. Journal of Xi’an Technological University, 2012, 32(11):874-885.)

[16] 宋涛, 王宏力, 陆敬辉. H∞滤波及其在INS/CNS组合导航系统中的应用[J]. 电子设计工程, 2011, 19(1):84-86.(Song Tao, Wang Hongli, Lu Jinghui. H∞Filter and Its Application in INS/CNS Integrated Navigation System[J]. Electronic Design Engineering, 2011, 19(1):84-86.)

[17] Xiong Zhi, Qiao Li, Liu Jianye, Jiang Bin. GEO Satellite Autonomous Navigation Using X-Ray Pulsar Navigation And GNSS Measurements[J]. International Journal of Innovative Computing, Information and Control, 2012, 8, (5(A)): 2965-2977.

[18] Simon D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches[M]. Wiley & Sons, 2006.

[19] 陈志刚, 陈刚, 仲昕,等. H∞滤波在微惯性组合导航系统中的应用[J].中国惯性技术学报,2009,17(4):456.(Chen Zhigang, Chen Gang, Zhong Xin, et al. Application of H∞Filter to MIMU/GPS Integrated Navigation System[J]. Journal of Chinese Inertial Technology, 2009,17(4):456.)

[20] 辜道威, 程鹏飞, 蔡艳辉,等. 卡尔曼滤波与H∞滤波在INS/GPS组合导航中的应用[J]. 全球定位系统, 2011, 36(3):26-28.(Gu Daowei, Cheng Pengfei, Cai Yanhui, et al. Application of Kalman Filtering and H∞Filtering for INS/GPS Integration[J]. CNSS Word of China, 2011, 36(3):26-28.)

An INS/CNS Integrated Navigation Method of Aerospace Vehicle Based on the H∞Filter

Shi Lijuan1, Xiong Zhi1, Wang Rong1, Yin Dequan1, Yu Feng2

1. College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China 2. College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

TheAerospacevehiclehasthecharacteristicsthatitsflightmissionisspecialanditsflightenvironmentiscomplex.Thus,asinglenavigationsystemcannotindependentlyprovidehigh-precisionparametersfortheASV.Asacompletelyautonomousnavigationtechnology,celestialnavigationsystemcanprovidehigh-precisionattitudeinformationanditserrordonotaccumulateovertime.Thenavigationaccuracyofaerospacevehiclecanbeimprovedbyusingcelestialnavigationsystemaidedinertialnavigation.Duetothecomplexflightenvironment,itishardtoobtainanaccurateerrormodelofactualnavigationsystemwhichcancauseadeclineintheperformanceoftraditionalKalmanfilter.AnINS/CNSintegratednav-igationmethodofaerospacevehiclebasedontheH∞filterisproposedinthispaper.ThemathematicalmodelofintegratednavigationsystemunderlaunchinertialcoordinateandH∞filtermodelarealsoestablished.ThesimulationresultsshowthattheproblemofinaccuratenoisemodelingofsystemcanbeeffectivelysolvedbyusingtheproposedmethodandtheaccuracyandreliabilityofintegratednavigationsystemofASVcanbeimprovedaswell.

Aerospacevehicle;Integratednavigation;Launchinertialcoordinate; H∞filter

*国家自然科学基金项目(61533009，61374115)；江苏省六大人才高峰资助项目(2013-JY-013)；江苏高校优势学科建设工程资助项目；中央高校基本科研业务费专项资金资助(NP2015406, NP20152212)；南京航空航天大学研究生创新基地(实验室)开放基金资助(kfjj20150315)

2016-05-03

施丽娟(1992-)，女，湖南岳阳人，硕士研究生，主要研究方向为惯性技术及组合导航；熊 智(1976-)，男，四川人，研究员，主要研究方向为惯性技术、景象匹配辅助导航、天文导航及惯性组合导航；王 融(1984-), 男，山西晋中人，讲师，主要研究方向为惯性技术及组合导航；殷德全(1992-)，男，吉林白山人，硕士研究生，主要研究方向为惯性技术及组合导航；郁 丰(1980-)，男，江苏海门人，副研究员，主要研究方向为惯性组合导航技术。

V19

A

1006-3242(2016)05-0046-06