准平衡滑翔轨迹在线规划与跟踪制导方法研究
杨 丁 刘 明 汤国建 刘鲁华 宋建强
1.国防科学技术大学航天科学与工程学院,长沙410073 2.空间物理重点实验室, 北京 100076
准平衡滑翔轨迹在线规划与跟踪制导方法研究
杨 丁1,2刘 明1,2汤国建1刘鲁华1宋建强1
1.国防科学技术大学航天科学与工程学院,长沙410073 2.空间物理重点实验室, 北京 100076

针对飞行器在线轨迹规划问题提出一种基于准平衡滑翔条件的轨迹在线规划方法及利用PID控制器实现的全状态跟踪制导方法。利用准平衡滑翔条件推导了高度、速度及航程等关键参数之间的解析关系,基于此条件结合飞行器当前状态与终端约束实现了物理可实现的滑翔轨迹快速规划;根据需要的速度和高度反馈量设计了PID控制器,实现纵向轨迹跟踪,通过飞行器航向误差走廊保证了飞行航向。仿真算例验证了该方法能实现轨迹在线规划,并对外部偏差具有较强的鲁棒性。 关键词 准平衡滑翔;在线轨迹规划;跟踪制导
滑翔飞行器通常在20~100km高度的临近空间内滑翔飞行,具有高空高速、灵活机动、快速响应以及强突防性能等优点。在全球侦察、远程精确打击等方面具备良好的应用前景,已成为世界各军事强国争相发展的重点。
在线轨迹规划技术是滑翔飞行器实现任务快速响应的前提与保障。传统轨迹规划方法通常通过建立飞行轨迹参数化模型,根据具体飞行任务,利用寻优算法迭代求解飞行器程序姿态角。国内外针对飞行器轨迹快速规划开展了大量的研究,采用的方法包括直接打靶法[1-2]、配点法[3-4]、动态逆方法[5-10]、滚动时域法[11-15]和伪谱法[16]等。文献[16]将轨迹优化问题转换为多段最优控制问题,并基于伪谱法实现滑翔飞行轨迹的优化。文献[17]基于给定的攻角剖面,利用拟平衡滑翔条件,对路径约束进行转换,将轨迹规划问题转化为单参数搜索问题,提高了解算效率。文献[18]基于纵向运动简化模型的微分平坦属性,降低系统设计的纬度,提出了一种基于微分平坦理论的三自由度轨迹生成方法。文献[19]针对RLV轨迹规划问题,将各种动态约束融入到轨迹设计中,通过动压剖面规划实现轨迹自动生成。然而,由于滑翔飞行器轨迹参数化模型高度非线性,迭代收敛慢,寻优效率低,此类方法通常仅适用于轨迹离线规划,难以满足飞行器在线轨迹规划的实时性要求。
本文充分利用飞行器滑翔飞行特性,利用平衡滑翔条件对原运动模型进行简化,并建立滑翔轨迹与飞行器受力之间的直接解析关系,实现滑翔飞行轨迹的快速规划。设计利用PID控制器跟踪已设计的参考轨迹,同时采用航向角误差走廊控制侧向运动,完成制导指令的自主生成。该方法完全避免了迭代搜索环节,有利于计算效率和可靠性的提高。
1 滑翔轨迹在线规划方案
1.1 轨迹在线规划问题描述
飞行器在长距离滑翔飞行过程中所受升力、离心力与重力达到一种平衡,其飞行攻角、过载以及高度等均处于一个平稳或缓慢变化状态,该过程可认为是平衡滑翔过程。基于准平衡滑翔条件设计参考轨迹需要满足以下约束:
1)实现预定航程;
2)终端速度满足俯冲下压或者进场着陆要求;
3)飞行过程中满足动压、过载以及热流密度等多种过程约束。
即根据当前飞行状态,通过轨迹自主在线规划,实现预期的终端能量和飞行航程。可以看出,滑翔轨迹规划问题实质是一个两点边值问题[3],根据预定的初始状态和终端状态,规划出滑翔轨迹。
1.2 轨迹在线规划逻辑设计
航天飞机再入轨迹规划中,首先确定攻角-速度剖面,然后优化设计阻力加速度-速度剖面以实现制导目标。类似地,滑翔飞行器同样采用BTT控制模式,通过对攻角和倾侧角的控制实现准平衡滑翔飞行,并满足预定航程以及终端速度的要求。准平衡滑翔可通过对高度-航程剖面的规划实现,终端速度可通过对速度-航程剖面的规划实现。在制导中,通过调节攻角与倾侧角大小实现对高度-航程、速度-航程剖面的跟踪控制,同时通过倾侧角方向调制,实现对航向的控制。
对于无动力滑翔飞行器,可以高度-航程剖面、速度-航程剖面作为轨迹规划设计变量,并通过倾侧角方向的调制,实现对横向位置的控制。
2 滑翔飞行器动力学建模与分析
2.1 飞行器动力学建模
轨迹在线规划问题可以看作为基准剖面的生成过程,考虑到地球旋转对滑翔飞行器受力影响较小,且实际飞行过程可进行制导修正。因此,轨迹规划中假设地球为均质不旋转圆球,三自由度运动方程可简化为:
(1)
式中,V为速度,h为高度,Θ为当地弹道倾角,θ为速度倾角,η为地心角,m为飞行器质量,D和L为气动阻力和升力,α为攻角,Re为地球半径,GM为地球引力常数。
2.2 准平衡滑翔运动特性分析
无动力滑翔飞行过程中,一方面需要通过控制飞行器升力,保证飞行器进行准平衡滑翔,并在保证待飞航程的条件下进行终端速度大小控制。滑翔飞行器作平衡滑翔飞行过程中,分析某一时刻受力,可认为[20]
(2)
结合式(1)中的速度倾角微分,可得出升力在纵向的分量和离心力与引力达到平衡

(3)
滑翔飞行器阻力加速度为

(4)
航程微分为
dS=Vdt
(5)
将式(3)与(4)代入式(5)可得:
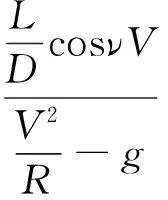
(6)
即
(7)
滑翔飞行器升阻比近似为恒值,即升阻比β为常数,

(8)
将式(8)代入式(7)可得:
(9)
式中,βcosν为飞行器升阻比在纵向的分量,简称为纵向升阻比,R可近似等于地球半径Re。可以看出,准平衡滑翔过程中,在终端速度约束下飞行器待飞航程与纵向升阻比成正比,因此待飞航程可通过设计纵向升阻比来实现,而纵向升阻比可直接用于解算控制量攻角和倾侧角。
3 轨迹在线规划与跟踪制导
3.1 飞行剖面自动生成算法
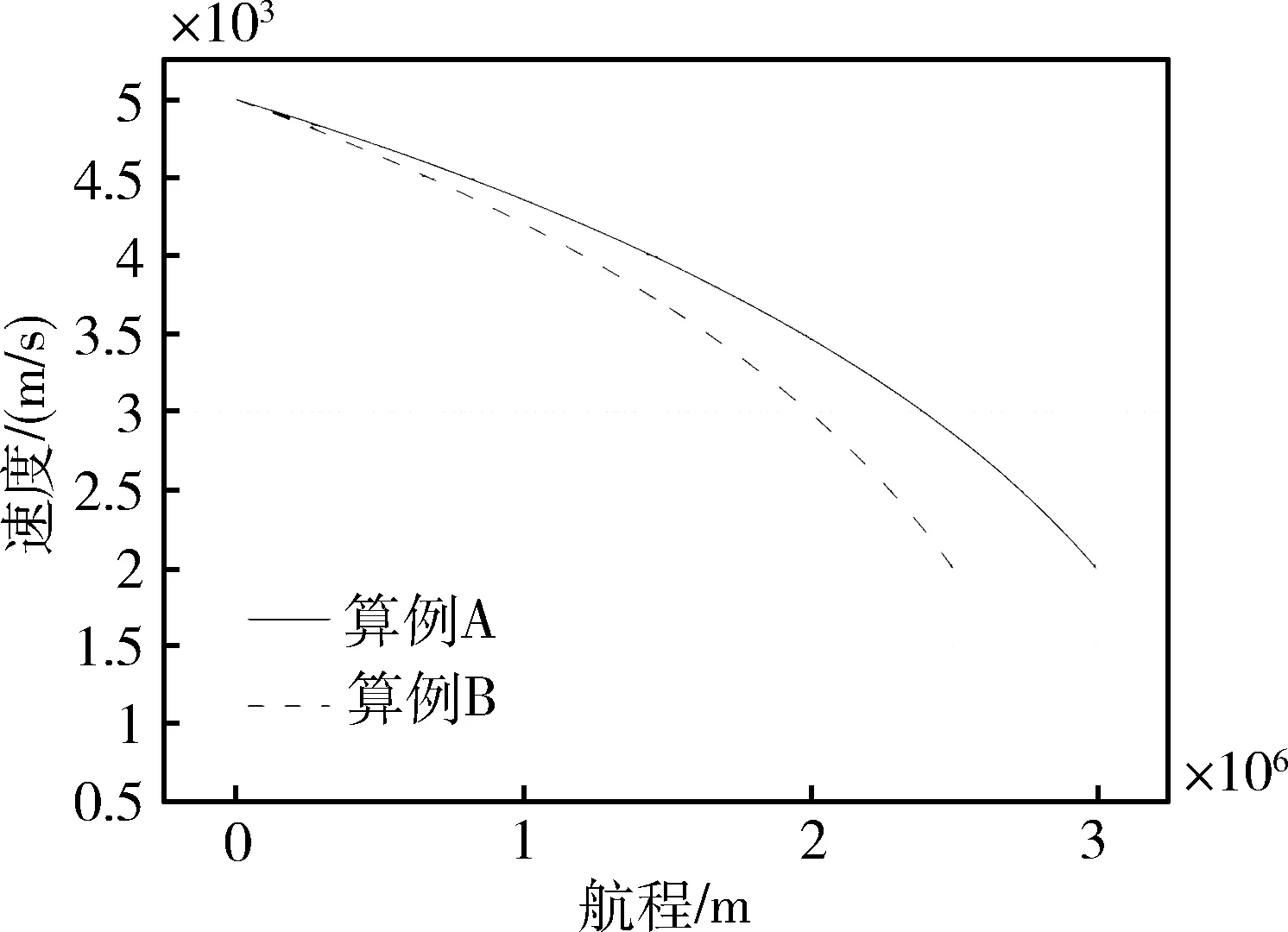
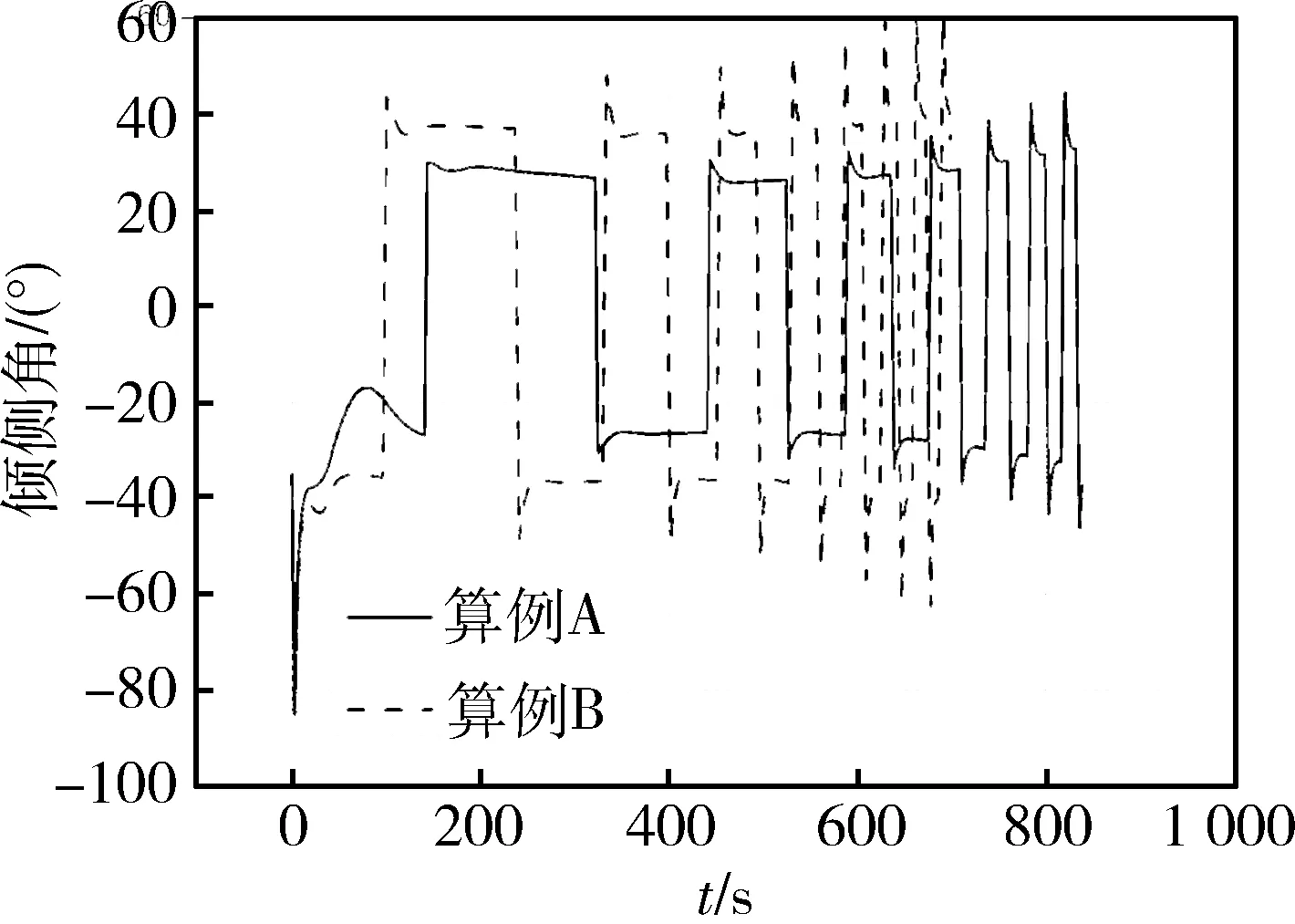
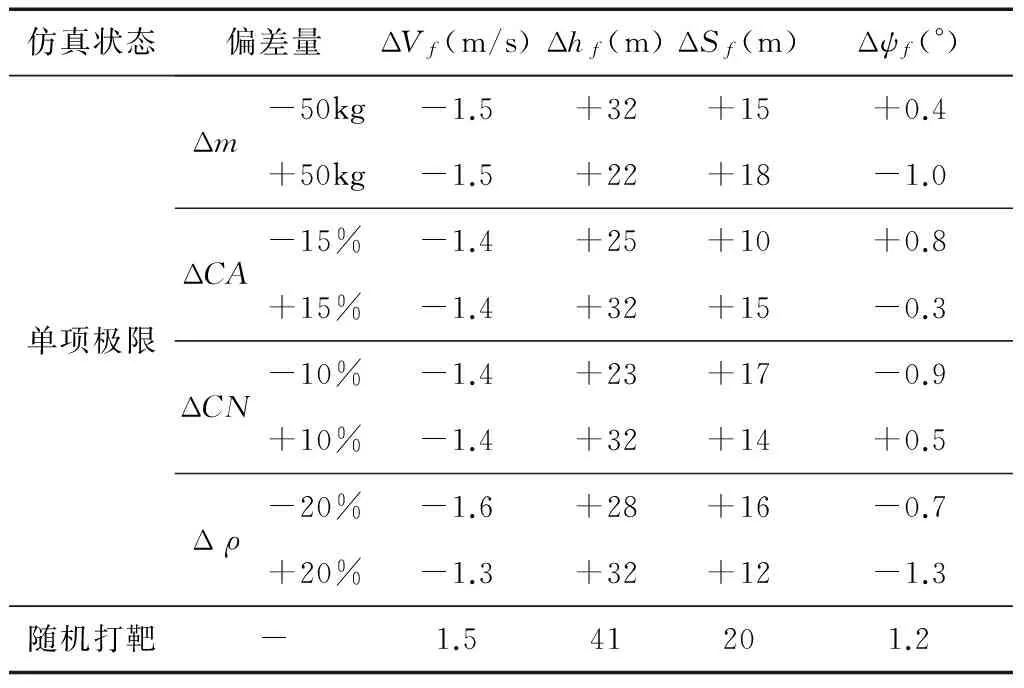
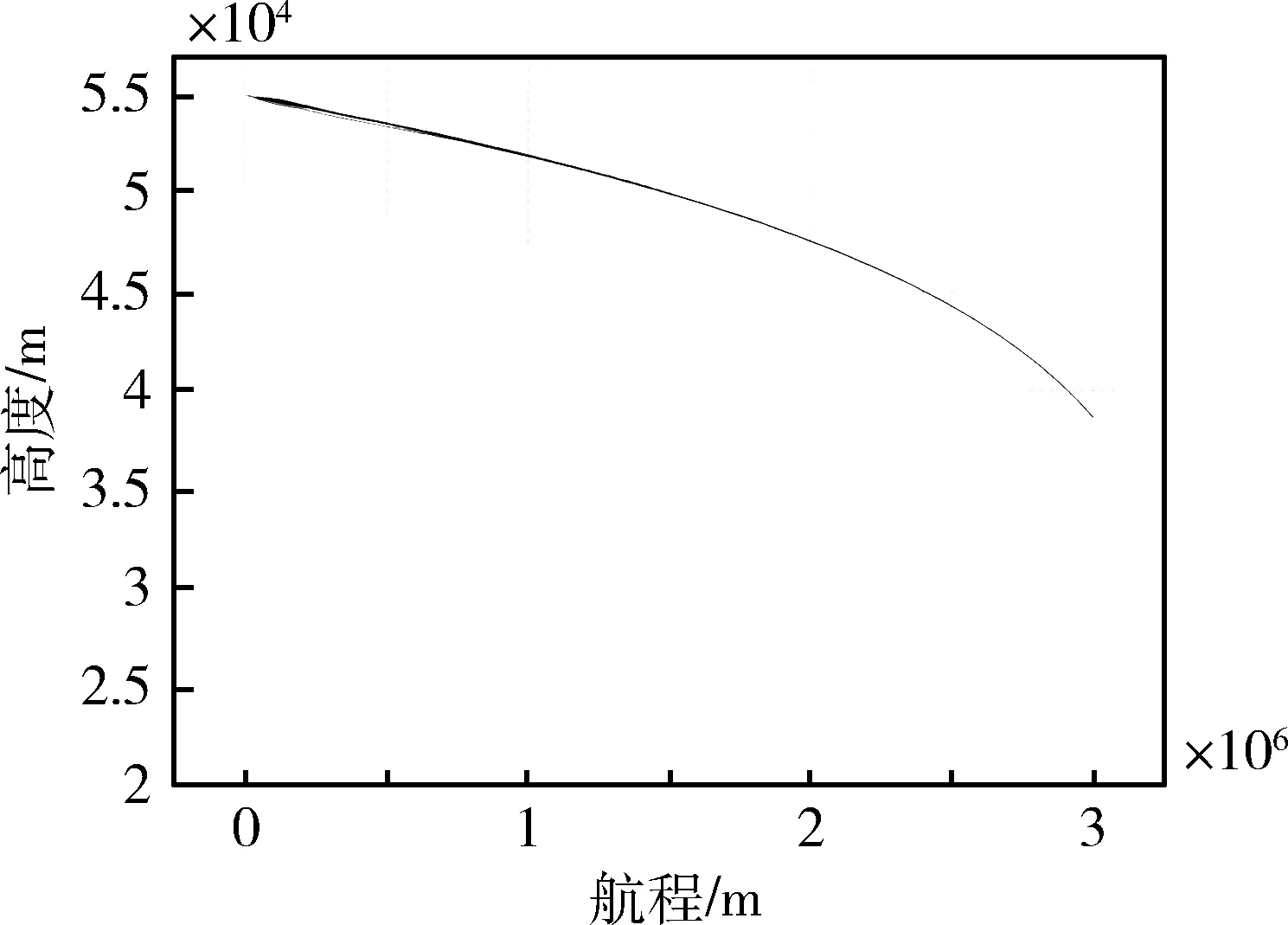
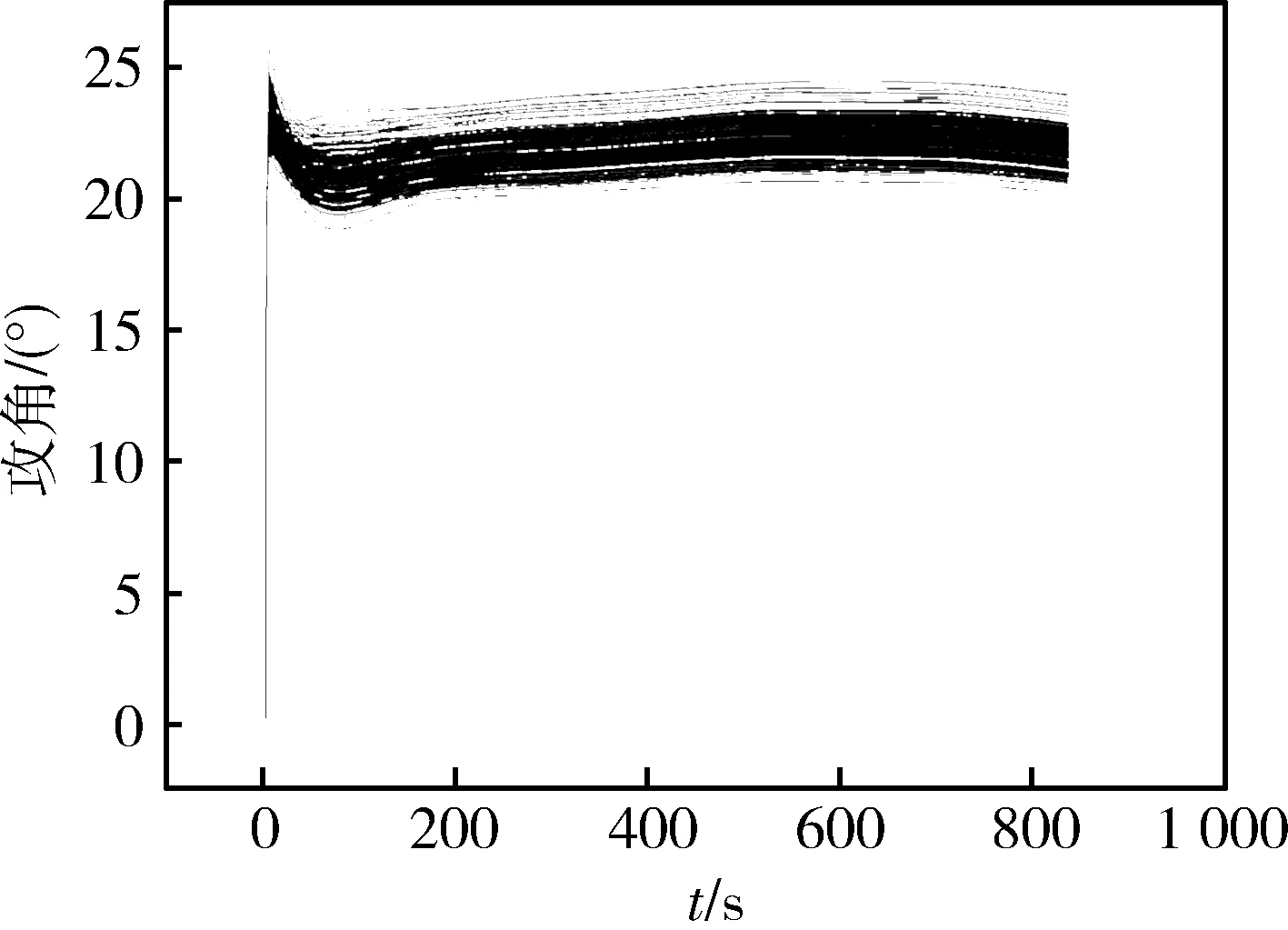
在相同初始速度V0的情况下,对应任意速度V(V (10) 根据终端航程和速度要求,可得出纵向升阻比 (11) 将式(11)代入式(10)可得平衡滑翔条件下的速度-航程剖面,计算公式如下: (12) 基于平衡滑翔满足升力与离心力和重力之间的平衡,因此高度随速度的变化关系为: (13) 将大气密度公式ρ(h)=ρ0e-λh代入式(13)可得 (14) 式中,λ取值1/7200。结合速度与射程的关系式(12)即可推导出平衡滑翔条件下的高度-射程剖面,计算公式如下 (15) 即在已知初始高度h0,速度V0,终端航程Sf以及速度Vf的情况下,可按式(12)和(15)求得准平衡滑翔的速度-航程、高度-航程剖面。 3.2 轨迹跟踪制导 以下采用PID控制器跟踪已设计的滑翔轨迹,进而生成攻角和倾侧角指令,利用攻角、倾侧角绝对值大小控制滑翔飞行器速度和高度,通过倾侧角的方向来控制滑翔飞行器航向,故可将制导问题分成纵向轨迹跟踪与航向控制两个问题。 (1) 纵向轨迹跟踪 纵向跟踪制导输入量包括高度、速度、射程及其变化率,输出的控制量为攻角和倾侧角绝对值大小。通过对飞行器运动方程小偏差线性化分析,可对高度和速度进行解耦控制,控制方程如下: (16) (17) 式中,hcx(S),Vcx(S)为规划出的高度-航程、速度-航程剖面,Kap,Kai,Kvp,Kvi,Kvd为增益系数。在倾侧角指令计算中,需要引入攻角环节以抑制攻角的调节对高度跟踪精度的影响。 (2) 航向控制 飞行器航向的控制通过倾侧角反转来实现,给出控制逻辑如下: (18) 其中,νi-1代表上一时刻倾侧角值,Δψbj为设计的航向角边界,可设计为一个随航程增加逐渐收敛的函数,在保证终端横向位置精度的同时减少倾侧角反转次数。 仿真中采用的滑翔飞行器对象质量为1500kg,气动参考面积0.9m2,最大升阻比约3.4。首先通过2个不同航程的算例对轨迹规划方法进行验证。 算例A:初始高度h0=55km,速度v0=5000m/s,当地弹道倾角Θ=0°。终端航程要求为3000km,终端速度vf=2000m/s。可用攻角范围为2°~30°,可用倾侧角为-90°~90°。 算例B:终端航程分别设定为2500km,其他条件同算例A。 仿真结果如图1~4所示。图1和图2给出了高度-航程、速度-航程剖面规划结果,可以看出,飞行高度、速度变化平缓,符合准平衡滑翔特征,终端速度、航程满足终端要求。图3和图4表明,在相同初始条件和终端速度要求下,飞行总航程越小,对应的攻角和倾侧角越大,这与2.2节通过纵向升阻比调节飞行航程的结论一致,验证了规划方法的可实现性及对不同航程任务的适应性。采用该方法无需循坏迭代,仿真时间均小于1s,可实现飞行器在线轨迹解算。 图1 高度-航程剖面规划结果 图2 速度-航程剖面规划结果 图3 攻角-飞行时间曲线 图4 倾侧角-飞行时间曲线 为进一步验证制导方法对偏差的适应性,在算例A的基础上加入飞行器质量偏差、轴向力系数偏差、法向力系数偏差和大气密度偏差等偏差量,并进行单项极限拉偏和随机打靶仿真。随机打靶各偏差量均按正态分布随机生成,仿真200次,统计得出终端精度3σ统计值。根据表1单项极限拉偏仿真结果和随机打靶结果,可知由于采用标称剖面跟踪制导方式,偏差因素对于终端控制精度影响不大。终端速度、高度、航程和航向角等制导精度较高:终端速度控制精度均小于2m/s,航程控制精度小于50m,航向角偏差小于1.5°。同时由图5~9可知,高度和速度剖面过程跟踪精度同样较高,航向角偏差随航向角走廊逐渐收敛,达到预期效果,可认为制导方法的有效性得到了验证。 表1 偏差状态下仿真数据 图5 高度-航程曲线(随机打靶) 图6 速度-航程曲线(随机打靶) 图7 攻角-飞行时间曲线(随机打靶) 图8 倾侧角-飞行时间曲线(随机打靶) 图9 航向角偏差-航程曲线(随机打靶) 根据滑翔飞行器准平衡滑翔轨迹特点,提出了一种基于高度-航程、速度-航程剖面的在线轨迹规划和制导方法。该方法可根据滑翔起始飞行状态和终端状态要求,在线实现轨迹规划,并通过控制攻角和倾侧角完成轨迹的自主生成。该方法相对传统轨迹迭代生成方法,避免了寻优迭代过程,算法更为简单,计算量小,可靠性高,具有较强的工程实用性。 [1] 傅瑜,马永青,崔乃刚.可重复使用助推飞行器轨迹优化研究[J].弹道学报,2011,23(4):5-9.(Fu Yu,Ma Yongqing,Cui Naigang.Research on Optimal Trajectory of Reusable Boost Vehicle [J].Journal of Ballistics,2011,23(4):5-9.) [2] Tu Lianghui, Yuan Jianping, Fang Qun, Luo Jianjun. Reentry Skipping Trajectory Optimization Using Direct Parameter Optimization Method[C]. 14th AIAA/AHI Space Planes and Hypersonic Systems and Technologies Conference, Canberra, Australia, Nov. 6-9, 2006. AIAA-2006-7993. [3] Albert L,Bruce A.Direct Optimization Using Collocation Based on High-Order Gauss-Lobatto Quadrature Rules[J].Journal of Guidance, Control and Dynamics,1996,19 (3):592-599. [4] Zimmermann Frank,Alise Anthony J.Aeroassisted Orbital Transfer Trajectory Optimization Using Direct Methods[C]. AIAA Atmospheric Flight Mechanics Conference,Baltimore,MD,1995. [5] Verma Ajay,Junkins John L.Inverse Dynamics Approach for Real-time Determination of Feasible Aircraft Reference Trajectories[C].AIAA Atmospheric Flight Mechanics Conference and Exhibit. Portland,OR,1999. [6] Verma Ajay,Oppenheimer Michael W,Doman David B.On-Line Adaptive Estimation and Trajectory Reshaping[C].AIAA Guidance,Navigation,and Control Conference and Exhibit.San Francisco, CA,USA,2005. [7] Lu Ping,Pierson Bion L.Optimal Aircraft Terrain-Following Analysis and Trajectory Generation[J]. Journal of Guidance,Control and Dynamics,1995, 18(3):555-560. [8] 谢愈,刘鲁华,汤国建,徐明亮.高超声速滑翔飞行器摆动式机动突防弹道设计[J].航空学报,2011,32(12):2174-2181.(Xie Yu,Liu Luhua, Tang Guojian,Xu Mingliang. Weaving Maneuver Trajectory Design for Hypersonic Glide Vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2011,32(12):2174-2181.) [9] Andrzej Zyluk.An Inverse Simulation Study on Wing Adapter Kit Dynamics and Control in Prescribed Trajectory Flight[C].44th AIAA Aerospace Sciences Meeting and Exhibit Reno,Nevada,9-12 January,2006. [10] Rick G Drury,James F Whidborne.A Quaternion-based Inverse Dynamics Model for Real-time UAV Trajectory Generation[C].AIAA Guidance,Navigation,and Control Conference. Chicago,Illinois,10-13 August,2009. [11] 任怀庆,粱艳春,孙亮.基于神经网络的滚动时域优化控制[J].北京邮电大学学报,2009,32(1):56-59.(Ren Huaiqing, Liang Yanchun, Sun Liang. The Receding Horizon Optimal Control Based on Neural Network[J]. Journal of Beijing University of Posts and Telecommunications, 2009,32(1):56-59.) [12] 曾剑新,周焰,何彦杰.一种飞行器在线航路重规划方法[J].空军雷达学院学报,2010,24(5): 333-336.(Zeng Jianxin,Zhou Yan, He Yanjie.A Method of Re-planning Aerocraft Online Route[J]. Journal of Air Force Radar Academy, 2010,24(5): 333-336.) [13] Kuwata Yoshiaki,Schouwenaars Tom,Richards Arthur.Robust Constrained Receding Horizon Control for Trajectory Planning[C].AIAA Guidance, Navigation,and Control Conference and Exhibit.San Francisco,CA;USA,2005. [14] Tam′As Keviczky,Gary J Balas.Flight Test of a Receding Horizon Controller for Autonomous UAV Guidance[C].American Control Conference.Portland, OR,USA,June 8-10,2005. [15] 张胜祥,裴海龙,刘保罗,李坚强.基于滚动时域优化的无人飞行器轨迹规划[J].计算机工程与应用,2008,44(35): 237-239.(Zhang Shengxiang, Pei Hailong,Liu Baoluo,Li Jianqiang. Trajectory Planning for Unmanned Vehicles Based on Receding Horizon Optimization[J]. Computer Engineering and Applications, 2010,24(5): 333-336.) [16] Jorris T R,Cobb R G.Three-dimensional Trajectory Optimization Satisfying Waypoint and No-fly Zone Constraints[J].Journal of Guidance,Control and Dynamics,2009,32(2):551-572. [17] Shen Z J,Lu P.Onboard Generation of Three-dimensional Constrained Entry Trajectories[J].Journal of Guidance,Control and Dynamics,2003,26(1):111-121. [18] 蔡伟伟,杨乐平,刘新建,朱彦伟.基于微分平坦的高超声速滑翔飞行器轨迹规划[J].国防科技大学学报,2014,36(2):62-67.(Cai Weiwei,Yang Leping,LiuXinjian,Zhu Yanwei. Differential Flatness Based Trajectory Planning for Hypersonic Glide Vehicle[J]. Journal of National University of Defense Technology,2014,36(2):62-67.) [19] 孙春贞,黄一敏.重复使用运载器在线轨迹生成技术研究[J].弹箭与制导学报,2008,28(8):261-265.(Sun Chunzhen,Huang Yimin. Onboard Trajectory Design for Reusable Launch Vehicle[J].Journal of Projectiles,Rockets,Missiles and Guidance, 2008,28(8):261-265.) [20] 卢宝刚,傅瑜,崔乃刚,单文昭.基于拟平衡滑翔的数值预测再入轨迹规划算法[J].哈尔滨工业大学学报,2015,47(1):14-19.(Lu Baogang,Fu yu,Cui Naigang,Shan Wenzhao.Numerical Prediction Method of Reentry Trajectory Planning Based on Quasi Equilibrium Glide Condition[J]. Journal of Harbin Institute of Technology,2015,47(1):14-19.) Quasi-Equilibrium Gliding Trajectory On-Borad Planning and Tracking Guidance Yang Ding1,2, Liu Ming1,2, Tang Guojian1, Liu Luhua1, Song Jianqiang1 1. College of Aerospace Science and Engineering,National University of Defense Technology, Changsha 410073, China 2. Science and Technology on Space Physics Laboratory, Beijing 100076, China Regardingtheglidingtrajectoryplanningprobleminvehicle,anon-boardtrajectorydesigningmethodbasedonquasi-equilibriumglidingandtheentirelyvariablestrackingwithPIDcontrollerapproachareproposed.Relativefunctionsbetweenheight,velocityandrangearededucedintheequilibriumglidemode.Basedontheflyingstate,theequilibriumtrajectorythatmeetsspecifiedmissionparametersandconstraintscanbeon-boardplaned.APIDcontrollerbasedonfeedbackvariablesofvelocityandheightisdesignedfortrackinglongitudinaltrajectory,andthelateralmotionisdeterminedbytheerrorcorridorofheadinganglebasedonbankanglerevision.Thenumericalsimulationresultsshowthatthemethodcanplanthetrajectoryon-boardandhasgoodrobustnesswiththeexteriordisturbances. Quasi-equilibriumgliding;On-boardtrajectorydesign;Trackingcontrol 2016-07-08 杨 丁(1984-),男,湖北崇阳人,高级工程师,博士研究生,主要研究方向为飞行动力学与控制;刘 明(1984-),男,湖北荆州人,工程师,博士研究生,主要研究方向为飞行动力学与控制;汤国建(1964-),男,江苏金坛人,教授,博士生导师,主要研究方向为飞行动力学与控制;刘鲁华(1978-),男,西安人,副教授,主要研究方向为飞行动力学与控制;宋建强(1969-),男,北京人,研究员,主要研究方向为飞行器设计。 V448.245 A 1006-3242(2016)05-0033-06

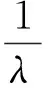
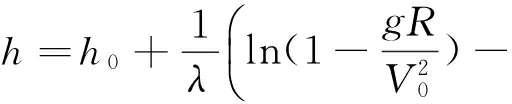

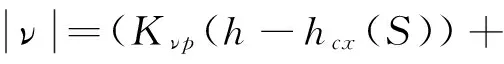
4 仿真分析





5 结论

