浅谈分数解决问题教学之感

韩来成

（福建省漳州市南靖县靖城中心径里小学）

浅谈分数解决问题教学之感

韩来成

（福建省漳州市南靖县靖城中心径里小学）

《义务教育数学课程标准》的总体目标指出：“初步学会运用数学的思维方式去观察、分析现实社会，去解决日常生活中和其他学科学习中的问题，增强应用数学的意识。教师应该充分利用学生以有的生活经验，引导学生把所学的数学知识应用到现实中去，以体会数学在现实生活中的应用价值。”

分数解决问题在小学数学第十一册教材中占有重要地位，它是培养学生能力和发展智力的重要内容。怎样使学生建立正确的解题思路，弄清分数解决问题中的已知条件和问题，分析分数解决问题的数量关系，把握解题规律和解题方法，将关系到学生的实际解题能力。那么，应如何开展有关分数解决问题的教学呢？在实际教学过程中，我深深地体会到要使学生真正学会解答分数解决问题应该做到以下几点。

一、找准单位“1”，理解分率，这是基础

在教学过程中，我深深地体会到只有找准单位“1”，才能正确解答分数解决问题。为此，在教学时，必须先让学生找准单位“1”，理解分率的意义，正确分析分率是谁与谁相比较，其中哪个量为单位“1”，即标准量，哪个量为比较量，即单位“1”几分之几对应的量，这是正确解答分数解决问题的基础和先提条件。在教学过程中，必须引导学生从重点句即表示分率关系的句子入手，正确理解单位“1”和分率的意义。因此，我常常分为以下几组训练，指导学生理解分率的意义。

1.单位“1”直接给出的

2.省略单位“1”

这种类型的特点是省略了分率的单位“1”。如“计划生产20000个零件，实际超额完成”，教师可以引导学生补充完整：“实际超额完成谁的”，然后再从补充完整的重点句入手分析：的单位“1”是谁？实际相当于计划的几分之几？这样学生就可以在已有的基础上顺利地进行知识的迁移。

3.比较量比较隐蔽的

4.根据上下句的联系，进行补叙、推理训练

二、借助线段图，找准分率的对应量，这是关键

在分数解决问题中有一个显著的特点：每个量有一个相对应的分率，解答分数解决问题可以从这一对应关系入手，但由于分数解决问题比较抽象，借助线段图可以清楚地表示出有关数量与标准量的对应关系，找到解题的途径。在教学时，可引导学生作图，同时引导学生看图分析，使学生的思维与作图同步，充分发挥线段图的直观作用。如：十月份烧煤210吨，比九月份节约，九月份烧煤多少吨？引导学生作图：

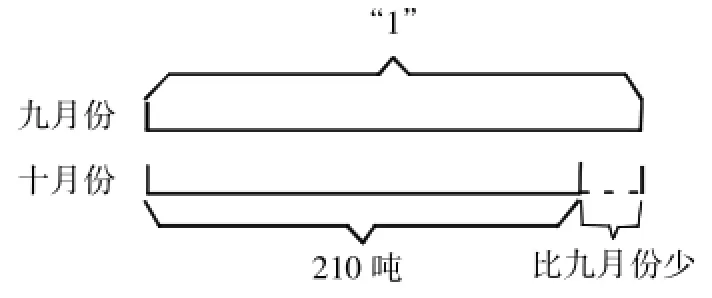
三、对比训练，掌握方法

对于容易混乱内容，可以有意识地设计一些变式题让学生练习、比较、分析它们的微差别，从而掌握解题规律，排除干扰。如：

通过对比，使学生理解题中分率和单位“1”都相同，但由于已知量不同解题方法也截然不同。前者单位“1”已知，后者单位“1”未知，所以前者求单位“1”几分之几对应量，用乘法，后者求单位“1”，用除法。

其次，在分析解决问题中，可将“分率”和“倍数”进行类似比较，帮助学生掌握算理。如：

①科技书100本，文艺书是科技书的3倍，文艺书有多少本？

③男职工有200人，是女职工的2倍，女职工有多少人？

通过比较，使学生体会到“分率”是“倍数”的扩充，而解题方法是一样的，从而使学生更好地掌握分数解决问题的解答方法。

四、转换单位“1”，发展思维

在掌握分数解决问题一般解法的情况下，教师还可引导学生进行单位“1”的转换，开拓思路，发展学生的思维。

其次，毕业班总复习时，还可以把单位“1”的转换方法与比例联系起来。如：甲乙两仓库存有货物132吨，如果从甲仓运走这时甲仓剩下的货物相当于乙仓的

，求甲乙两仓原有货物多少吨？

引导学生分析：题中只有一个具体数量132吨，而题中单位“1”不一致，必须进行单位“1”的转换，题中甲仓运走，甲仓剩下的货物是乙仓的，说明甲仓的等于乙仓的，也就是甲×=乙×。这时，可引导学生利用比例的基本性质统一单位“1”，甲仓货物相当于乙仓的，132吨相当于乙仓的倍，则乙仓货物为吨，甲为：132-72=60吨。

通过单位“1”的转换，可以排除学生的思维定式，开拓思路，发展学生的思维，扩大学生的知识面，提高学生的解题能力。

总之，在教学中，我们要引导学生灵活运用，用多种方式分析、解决，形成学生自己解决问题的能力。

·编辑温雪莲