静爆冲击波在空气中的传播规律

华　雨，于纪言，张　庆，李兴隆

(1.南京理工大学 智能弹药技术国防重点科学实验室，南京　210094；2.中国工程物理研究院 化工材料研究所，四川 绵阳　621900)



静爆冲击波在空气中的传播规律

华雨1，于纪言1，张庆1，李兴隆2

(1.南京理工大学 智能弹药技术国防重点科学实验室，南京210094；2.中国工程物理研究院 化工材料研究所，四川 绵阳621900)

摘要：通过对爆炸冲击波在空气中传播的已有研究成果进行了对比分析，提出了一个能较好描述冲击波超压峰值与当量比例距离关系的解析式。通过静止装药爆炸试验，测得距爆心不同距离处的超压-时间曲线，实测值与理论值能较好吻合，但是在距离爆心较近处仍存在一定偏差，并且实测曲线受到反射波影响较大。

关键词：爆炸冲击波；超压峰值；静止装药；比例距离本文引用格式：华雨，于纪言，张庆，等.静爆冲击波在空气中的传播规律[J].兵器装备工程学报，2016(7):168-172.

Citationformat:HUAYu，YUJi-yan，ZHANGQing，etal.StudyonPropagationLawofStaticExplosionWaveinAir[J].JournalofOrdnanceEquipmentEngineering,2016(7):168-172.

相关研究表明，爆炸产生的破坏作用主要是由冲击波产生的。作为某些战斗部的主要杀伤因素之一，冲击波能够在较远距离对目标起杀伤和破坏作用，冲击波的确定对于这类战斗部的威力评价有着十分重要的作用[1]。冲击波是一种介质状态(压力、密度、温度等)突跃变化的强扰动传播，最常见的形式是空气冲击波，其传播速度大于声速。多数情况下，冲击波的破坏伤害作用是由超压引起的。超出周围压力的最大压力即为峰值超压。冲击波的破坏作用主要由峰值超压、持续时间和冲量3个特征参数衡量。冲击波破坏伤害准则主要有超压准则、冲量准则和超压-冲量准则等，其中最常用的是超压准则。因此对超压峰值的预测研究有着重要的工程价值和军事意义[2]。

由于影响爆炸冲击波参数的因素十分复杂，现有的不同学者提出的经验公式彼此之间存在不小的差异。本文针对静爆试验的爆炸冲击波在空气中的传播规律进行研究，对不同学者的经验公式进行对比分析，提出一个能较好描述冲击波超压峰值与当量比例距离关系解析式。通过静爆试验，将实测值与理论值进行对比并给出超压-时间曲线。

1现有冲击波超压峰值参数的研究

高爆炸药在空气中爆炸时,形成了一团瞬间占据炸药原有空间的高温高压气体[3]。这团气体猛烈地推动周围静止的空气,同时产生一系列的压缩波向四周传播,各个压缩波最终叠加成冲击波。

图1为自由空气中的理想冲击波波形，即P-t曲线[4]。由图1可见，在冲击波到达之前，该处的压力等于大气压力P0。冲击波在时间Ta到达该处后，压力经过时间Tr由大气压力突跃至最大值。压力最大值与P0的差值即被称为入射超压峰值Pso。波阵面通过后压力迅速下降，在经过时间Td压力经指数衰减至大气压力并继续下降，直至出现负超压峰值，再在一定时间内又逐渐回升至大气压力。

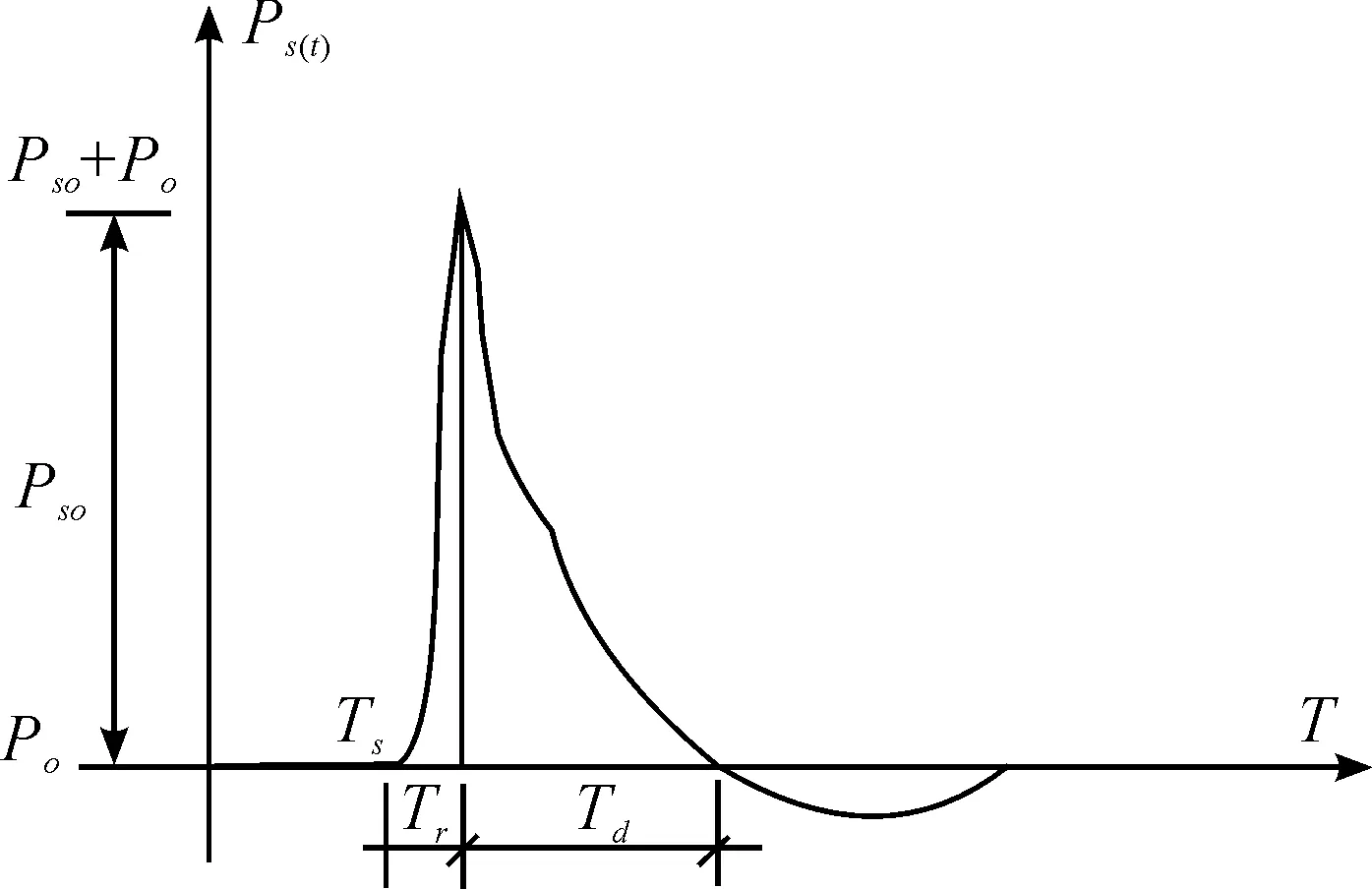
图1　自由空气中的理想P-t曲线

实际情况中静止装药在地面上空发生爆炸，随着冲击波的传播，入射波被地面反射面加强形成反射波，由于初始波(入射波)与反射波的相互作用形成马赫波阵面，因此在实际情况中，一个点的超压-时间关系通常是由入射波超压和经过反射的入射波超压相互作用构成[5]。

人们对高爆炸药爆炸产生的冲击波的传播规律主要用冲击波压力、超压峰值、冲量、持续时间等冲击波参数描述，其中最重要的参数是超压峰值[4]。目前比较简单但是公认的、常用的方法，即用当量比例距离来表达冲击波的各项参数[6]。1973年，Baker提出用TNT当量比例距离估算超压，即冲击波超压可由等效TNT当量W以及距地面上爆炸源点的距离R来估算，当量比例距离Z定义为

式中：R为测点与爆心之间的距离(m)；W为等效TNT药量(kg)。

目前很多研究者对空气中的冲击波参数进行了研究并提出了相应的经验预估公式。这里简要介绍一下几个常见的经验公式。

Brode 建议高爆炸药爆炸冲击波峰值超压(MPa) 的表达式为[7]

Henrych 建议空气中冲击波 的峰值超压(MPa)表达式为[8]

Mills介绍了高爆炸药冲击波峰值超压 (MPa)的一种表达式[7]

叶晓华[5]提出 TNT 球形装药在无限空气中爆炸时的冲击波峰值超压 (MPa) 的计算式为

ChengqingWu和HongHao提出高爆炸药冲击波峰值超压(MPa)的一种表达式为[9]：

萨多夫斯基根据模型相似律理论建立公式，由试验确定系数，得到高爆炸药冲击波峰值超压(MPa)的表达式为[10]

由于爆炸问题的复杂性，冲击波超压峰值的各种经验预测方法难免会带来一些偏差。小当量比例距离范围内，在对数坐标中，不同方法预测的冲击波超压峰值与当量比例距离的关系对比如图2所示。

图2　不同参考文献的冲击波超压峰值-当量比例距离关系比较

由图2得知，当当量比例距离Z大于1 m/kg1/3时，各个公式预测的结果比较接近，其中Mills和Wu C.& Hao H预测的结果相较其他4个公式略微偏高。随着当量比例距离的减小，各个公式给出的结果的偏差逐渐偏大，Mills公式的值偏高，而Henrych公式的值偏低，且在Z小于0.8的情况下结果与其他公式偏差较大。在小当量比例范围内，Brode公式和文献5推荐的公式比较吻合。

通过以上对比分析可见，将萨多夫斯基推荐的公式与文献[5]中的公式相综合可以较好地描述冲击波超压峰值和当量比例距离的关系，其解析式为

其中：Z为当量比例距离；P为理论冲击波超压峰值。

2静爆试验与数据分析

2.1试验设置

试验装药选用8701炸药，装药结构为长200 mm，直径80 mm的圆柱体，壳体材料为50SiMnVB钢，起爆方式为一段中心起爆。在上述装药尺寸下，TNT炸药的质量为1.81 kg。结合上述提出的球形装药在无限空气介质中爆炸的超压公式可得到表1。

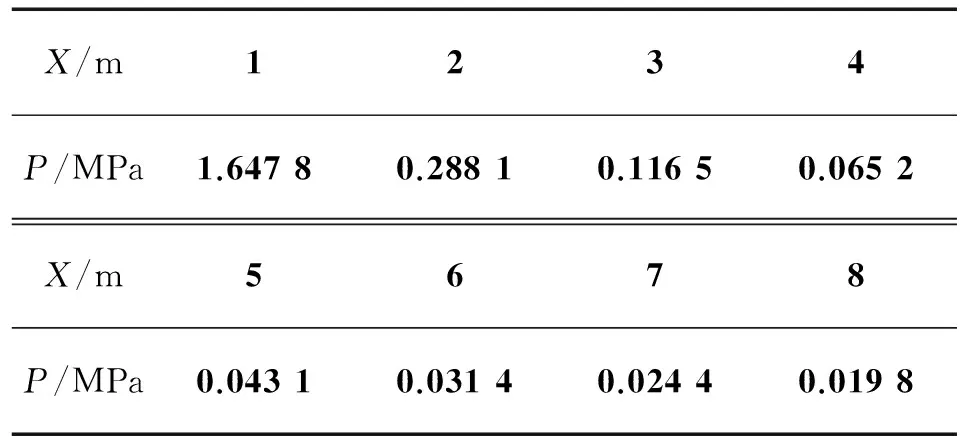
表1　距爆心不同距离的理论超压峰值

静爆试验采用中北大学设计的冲击波存储测试仪，它运用存储测试技术，将电源、A/D转换器、存储器、控制模块及数据通讯接口集成为一体，能够脱离计算机独立工作；采用自带电池供电，放置于测点附近，减少了实验现场布线的工作量，大大降低了传输线缆受到损坏和干扰的程度，提高了数据获取的成功率。内部的压力传感器选用美国PCB公司的113B21型号压力传感器，采样率106Hz，具体参数如表2所示

在静爆试验中共设置了5个探测点位，用来记录距离爆心2 m、3 m、4 m、5 m、6 m的超压-时间曲线，布点位置根据距爆心的位置呈弧状排开，具体位置如图3所示。

表2　传感器113B21参数

图3　实验现场布点图

2.2结果数值对比

图4(a)、图4(b)、图4(c)、图4(d)、图4(e)分别是第一次起爆时所测距爆心2 m、3 m，4 m，5 m，6 m处的冲击波超压-时间曲线。对比图1和图4可见， 由于实验场地地平面并不平整，实际所测得的波形受到反射波的影响颇为明显，几乎每一个传感器都受到了不止一次的反射波的冲击，并且距离爆心越近处，受反射波的影响越大，如图4(a)所示，距爆心2 m处的传感器受到多次反射波干扰。但反射波主要干扰对冲击波持续时间的测量以及冲击波冲量的计算，对于冲击波峰值的测量影响并不大。在总体上，曲线的走势和理想曲线一致，均是冲击波到达传感器后，压力经过极短的时间由大气压力突跃至最大值即峰值超压。波阵面通过后压力迅速下降直至出现负超压峰值，在一定时间内又逐渐回升至大气压力。

3次试验所用炸药以及测试条件完全一致，受篇幅限制，第二次和第三次起爆的曲线不再详细给出，表3即为3次起爆的超压峰值与理论超压峰值的数据汇总对比，拟合成折线图即如图5所示。结合表3和图5可以看出，Mills和Wu&Hao预测的结果与实测值相比明显偏高，尤其是在距爆心较近处，HenRych公式的值相对偏低，Brode公式在距爆心较远处与实测值偏差较大，而将萨多夫斯基与文献5综合的公式与实测值基本一致，曲线走势吻合较好，但在距离爆心较近的地方，预测值略有偏高，曲线也相对更陡，而试验曲线则相对平缓，考虑到试验现场的环境以及装药误差等因素的影响，总体上在误差范围内。

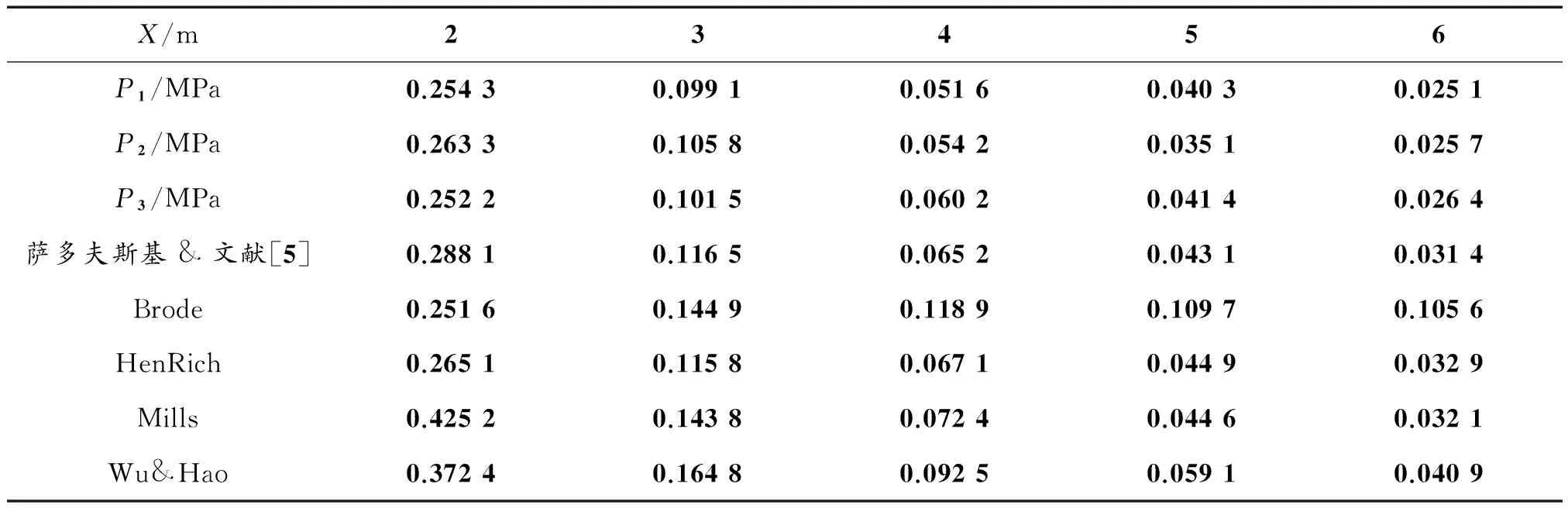
表3　实测超压值与理论预测值数据汇总

图5　试验实测值与理论预测值对比

3结论

现有的对冲击波在空气中传播规律的研究已经取得了一定的成果，但是不同学者的经验公式结果还存在不少差异，特别是距离爆心越近，差异越大。本研究对不同学者关于冲击波超压峰值预测的对比分析，总结出能较好描述冲击波超压峰值与当量比例距离关系的表达式，通过三轮静止装药爆炸试验，测得距爆心不同距离处的超压-时间曲线，将实测值与理论值对比，得出以下结论：

1) 静爆试验受反射波的影响，干扰了冲击波持续时间的测量，且距离爆心越近，受反射波影响越大。但对超压峰值测量的影响很小。

2) 实测值与总结出的经验公式能较好吻合，能较好地描述实际静爆时冲击波超压峰值与当量比例距离的关系。

3) 实测值与经验公式预测值在距爆心较近处仍存在一定的偏差，有必要通过更多的实验来对经验公式进行进一步的修正工作。

参考文献：

[1]牛余雷.炸药爆轰参数与空中爆炸冲击波超压的关系 [J].火炸药学报,2013,36(4):42-45.

[2]傅智敏.爆炸冲击波伤害破坏作用定量分析[J].消防科学与技术,2009,28(6):390-395.

[3]AHMED FAHMY FARAG TOLBA.Response of FRP-retrofitted reinforced concrete panels to blast loading[D].Ottawa,Canada:Carleton University,2001.

[4]张广福.爆炸冲击波无限空气领域传播的数值模拟研究[J].山西化工,2009,29(1):43-46.

[5]叶晓华.军事爆破工程[M].北京:解放军出版社,1999.

[6]冯海龙.爆炸冲击波的简化计算方法概述[J].山西建筑,2010,36(21):69-70.

[7]张守中.爆炸与冲击动力学[M].北京:兵器工业出版社,1993.

[8]亨利奇.爆炸动力学及其应用[M].北京：科学出版社，1987.

[9]WU C,HAO H.Modeling of simultaneous ground shock and airblast pressure on nearby structures explosions[J].IntJ Impact Eng,2005,31(6):699-717.

[10]张纯学.动能武器及其发展[J].飞航导弹,2004(8):21-24.

(责任编辑周江川)

收稿日期：2016-02-09；修回日期：2016-03-09

作者简介：华雨(1993—),男,硕士研究生,主要从事机电控制和传感器方面的研究。

doi:10.11809/scbgxb2016.07.036

中图分类号：O382+.1

文献标识码：A

文章编号：2096-2304(2016)07-0168-05

StudyonPropagationLawofStaticExplosionWaveinAir

HUAYu1，YUJi-yan1，ZHANGQing1，LIXi-long2

(1.MinisterialKeyLaboratoryofZNDY,NanjingUniversityofScience&Technology,Nanjing210094,China; 2.InstituteofChemicalMaterials,ChinaAcademyofEngineeringPhysics,Mianyang621900,China)

Abstract:Through the comparative analysis of the existing research results of blast shock wave propagation in air, the analytical formula of the relationship between the peak value of overpressure and the proportional distance was summarized. Through the static loading explosive test, we measured overpressure time curves from the explosion of heart at different distances. The measured values are in good agreement with the theoretical data, but from explosive center nearer, there still exist certain deviation, and the measured curve by reflection wave effect is large, so it is necessary to further research on the explosion shock wave.

Key words:explosion wave; peak overpressure; static power charge; scaled distance

【基础理论与应用研究】