基于粒子群算法的多拦截器分配优化策略*

李瑞康 史秉政 张 召 荆武兴

1.上海机电工程研究所，上海201109 2.哈尔滨工业大学，哈尔滨150001



基于粒子群算法的多拦截器分配优化策略*

李瑞康1史秉政1张 召2荆武兴2

1.上海机电工程研究所，上海201109 2.哈尔滨工业大学，哈尔滨150001

研究了大气层外拦截多目标分配策略。基于目标威胁度和拦截有效程度建立目标分配模型，设计了一种基于粒子群算法的目标分配策略，针对算法存在的缺陷，利用遗传算法交叉思想对粒子更新策略进行了改进，并对其性能进行了数值仿真分析。结果表明，改进的算法能有效克服基本粒子群算法的弱点，具有收敛性快、稳定性好的特点，没有出现优化退化现象且对不同拦截场景具有较强适应能力。 关键词 多拦截器；目标分配策略；遗传算法；粒子群算法

为了克服弹道导弹中段拦截过程中多目标识别难题，美国提出一种MKV(MKV，Multiple Kill Vehicle)技术，它通过运载器将一个携带多个微小型拦截器的母舱送至指定位置，对一定范围内所有威胁目标实施有效杀伤[1]。杀伤过程中对拦截器进行目标分配是研究工作的重点之一，武器-目标分配(WTA，Weapon-Target Assignment)问题在当今作战决策和火力运用中具有重要地位。

WTA问题主要包括分配建模和分配算法设计2大部分[2-3]。面对日益复杂的战场环境，对目标分配策略的研究经历了传统算法到智能算法、静态分配到动态分配的过程[4-10]。在算法设计方面，文献[4-5]分别采用不同粒子群混合算法对空战中合作目标拦截火力进行分配设计，取得了较好的效果，其他的一些智能方法，如蚁群、模糊及离散差分等在解决某一特定问题上也得到了较好的研究[6-8]，体现了智能算法在复杂战场环境下的设计优势。此外，动态武器-目标分配(DWTA，Dynamic Weapon-Target Assignment)问题也逐渐得到研究[9-10]，但相对静态分配问题，需要考虑时间和随机因素影响，求解更加复杂，目前更多处于探索阶段，成果并不多见。

与传统防空领域面对的作战环境不同，本文研究了弹道导弹中段拦截中WTA策略问题，需要考虑非合作、大相对速度及多拦截数量等因素，要求目标分配策略具有快速性和稳定性。本文尝试利用粒子群算法设计分配策略，并对其进行了改进，以提高分配性能，通过与遗传算法分配结果[11]比较，改进后的分配算法显示出更优的综合性能。

1 多拦截器目标分配模型

假设我方有m个子拦截器，现探测到n个来袭目标，并对其进行拦截。现规定： 1)每个子拦截器只能拦截1个目标； 2)每个目标可分配给任何子拦截器，但不同子拦截器拦截同一目标的拦截有效程度不同。

设计决策变量：

(1)

则目标分配基本优化模型为[11]：

(2)

其中：F(V)为性能函数，Wj为第j个目标的威胁程度，Pij为第i个子拦截器拦截第j个目标的拦截有效程度。

目标威胁程度Wj可以通过运动、红外和电磁等特征进行评估，拦截有效程度Pij通过零控脱靶量的相对量进行评估，可参阅相关文献，不再赘述，性能评估时认为Wj和Pij是已知。

2 基于粒子群算法的目标分配实现

粒子群算法(PSA, Particle Swarm Algorithm)基本概念源于对鸟群觅食行为的研究，它从生物种群行为特性中得到启发并用于求解最优化问题。在粒子群算法中，每个优化问题都可以想象成d维搜索空间上的一个点，称之为“粒子”，所有的粒子都有一个被目标函数决定的适应值，每个粒子还有一个速度决定其飞翔的方向和距离，然后其他粒子“追随”当前的最优粒子在解空间搜索。

由n个粒子组成的群体对Q维空间进行搜索，每个粒子表示为：Xi=(Xi1,Xi2,...,XiQ)，i=1,2,...,n，每个粒子对应的速度可以表示为vi=(vi1,vi2,...,viQ)，每个粒子在搜索时要考虑以下2个因素：

1)自己搜索到的历史最优值pi，pi=(pi1,pi2,...,piQ)；

2)全部粒子搜索到的最优值pg，pg=(pg1,pg2,...,pgQ)，注意这里的pg只有一个。

粒子群算法的位置速度更新公式如下：

(3)

(4)

其中：ω是保持原来速度的系数，称为惯性权重；c1是粒子跟踪自己历史最优值的权重系数，表示粒子自身的认识，称为“认知”，通常取2；c2是粒子跟踪群体最优值的权重系数，表示粒子对整个群体的认识，称为“社会认知”或“社会”，通常取2；ξ，η是[0,1]内均匀分布随机数；系数r称为约束因子。

(5)

式中：ωmax，ωmin为惯性权值最大、最小值；iter为当前迭代次数，itermax为总的迭代次数。

提高初始种群对设计空间的覆盖性(即种群能全面的表征设计空间)有利于提高粒子群多样性和算法搜索效率。本文将应用均匀设计对粒子群算法的粒子种群进行初始化。

均匀设计表的构造方法比较多，好格子点法被广泛使用，该方法能产生试验数和水平数为n、列数为m(m是n的欧拉数)的设计表，其构造方法如下：

1)给定试验数n，找比n小的正整数h，要使n与h的最大公约数为1，将符合条件的正整数组成列向量h=[h1h2…hm]T；

2)均匀设计表的第i列元素为

uij=jhi[modn]

(6)

式中：[modn]表示同余运算后取整，如果jhi大于n，则其要减去n的一个合适倍数，使差落在[1,n]之间。

uij可以递推生成：

uij=hi,

(7)

式中：i=1,...,n,j=1,...,m。

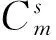
CD2(P)=

(8)

从均匀设计表Un(nm)中选取s列来构成试验方案，要使试验方案的中心化L2-偏差(即CD2)最小。

粒子群算法的本质是利用个体极值和全局极值2个信息，来指导粒子下一步迭代位置。对于 WTA问题，其解用矩阵表示，为了简化问题，采用十进制编码方式，每个粒子长度与拦截器所携带的MKV数目相等，这样每个粒子对应一种分配方案，如[5 3 4 1 2]表示将目标5分配给MKV_1,目标3分配给MKV_2，依次类推，这样做的目的是使每个拦截器都有目标与之对应，且形成映射关系。

假设MKV和目标数量均为20个，每个目标的威胁度为：

W=[0.17 0.97 0.76 0.62 0.48 0.970.330.84 0.54 0.25 0.45 0.76 0.43 0.64 0.57

0.12 0.25 0.76 0.84 0.76]

(9)

每个MKV对每个目标的拦截有效程度为

P=[Pij]20×20

(10)

本文假设P是给定的，下同。

按照上述推理，直观想法是对粒子位置向上或向下取整，假设粒子个数为100个，迭代次数为400次，得到分配结果如图1所示。

从仿真结果可以看出，一些目标未被很好分配，即认为不拦截，如序号3，8，19目标威胁程度很高，但并未被分配，显然算法存在不合理之处。这是由于设计过程中没有给优化加入约束，仅以适应度函数(目标函数F(V))值最大为目标，而适应度函数值是威胁程度W和拦截有效程度P的函数，当拦截有效程度过低时，即使威胁程度很高也会在优化中被舍弃。所以，有必要对粒子群进行约束，并加以改进。

图1 基本粒子群目标分配方案(m=n)

3 粒子更新策略

对于WTA问题，若按基本粒子群算法，其速度难于表达，这里引进遗传算法交叉操作思想：让当前所有解与个体极值和全局极值分别作交叉操作，产生的解为新的位置；针对粒子群算法容易陷入局部最优解，且效率不高的问题，考虑遗传算法中变异操作思想，在经过交叉操作后，再进行变异操作；同时，为了避免优化过程出现退化现象，在产生新粒子后，加入一步粒子判断，如果新粒子的适应度值小于旧粒子，则不进行更新，该个体仍使用旧粒子。

令P1表示当前解，P2表示个体极值和全局极值，具体策略如下：

交叉策略：

1)随机产生一个交叉点；

2)用P2交叉点之后的基因段替换掉P1交叉点后的基因段。

变异策略：

1)随机产生变异点和变异值；

2)将P1上与变异值相同的首个基因用变异点处的基因替换；

3)将P1上变异点处的基因用变异值替换。

4 仿真算例分析

依照上节给出的粒子更新策略，条件同上，重新对目标分配方案进行仿真，结果如图2所示。从仿真结果可以看出，分配取得比较合理的效果，说明改进后的粒子群算法是有效的。

图2 改进粒子群目标分配方案(m=n)

同理，考虑MKV为20个，目标为16个时，其它参数设置同上(限于篇幅，W,P不再列出)，得到的分配方案如图3所示。

仿真结果说明，在拦截器与目标数不对等的情况下，设计的目标分配算法仍然有效，说明算法具有较好的适应性。

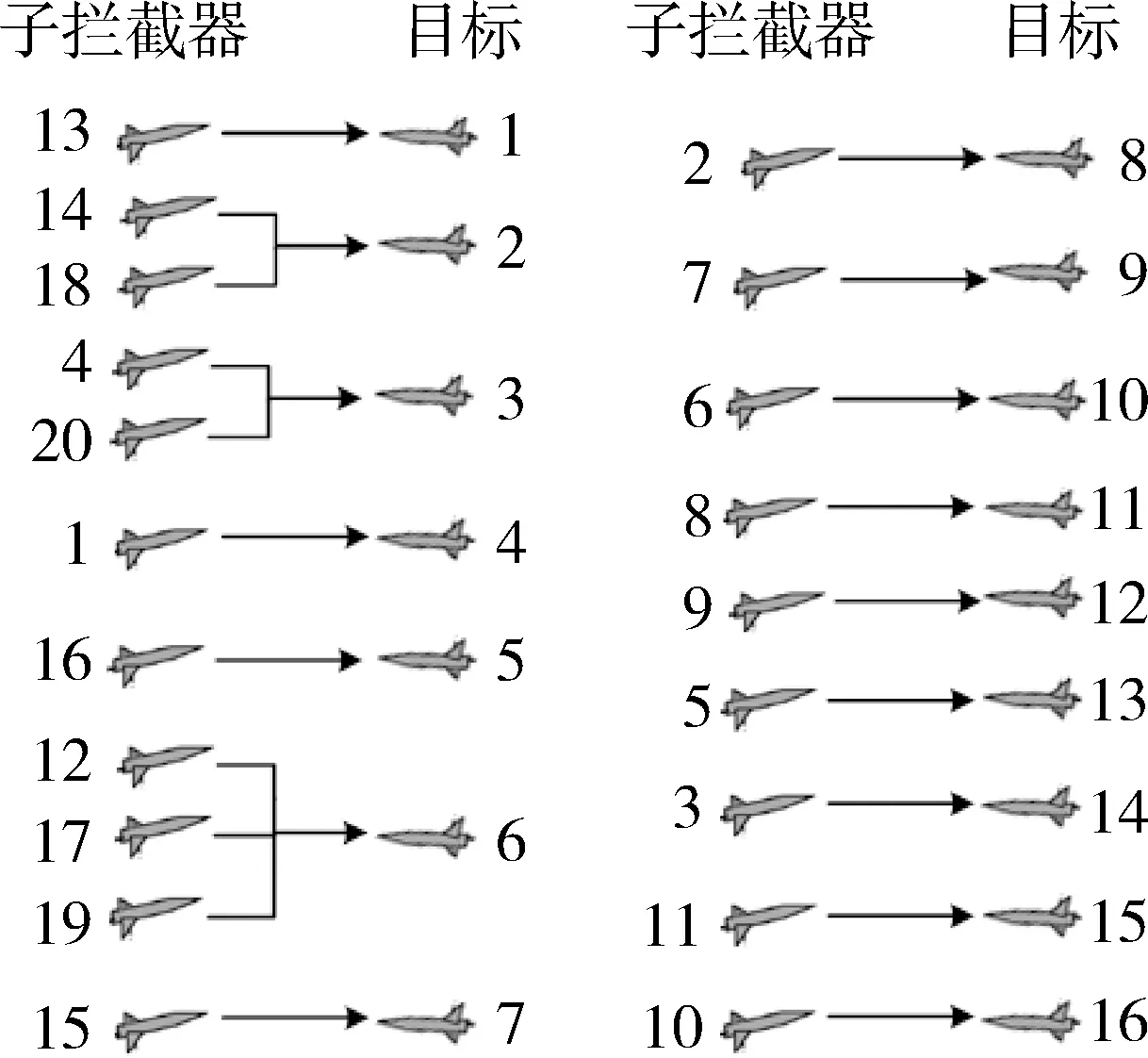
图3 改进粒子群目标分配方案(m≠n)

假设MKV与目标数量均为20个，运行单次改进粒子群算法与遗传算法，改进粒子群算法中，粒子个数为100个，迭代次数为400；遗传算法中个体数目为100个，最大遗传代数为400，交叉率取0.7，变异率取0.05，两种分配算法的适应度值变化曲线对比如图4所示。从图中可以看出，改进粒子群算法获得的最终适应度值为10.59，要大于遗传算法的10.52，两者收敛均较为平稳，但改进粒子群算法在收敛速度上要比遗传算法快，如迭代50次，改进粒子群算法的适应度值达到10.1，达到最大值的95.4%，而遗传算法仅为9.7，为最大值的92.2%。在相同配置机器上，2种算法分别连续运行100次，利用统计方法对分配性能进行对比，遗传算法总运行时间为209.68s，改进粒子群算法为219.96s，相比遗传算法慢4.9%，得到最终适应度值高于10.5的情况，遗传算法为54次，改进粒子群算法为99次，概率分别为0.54和0.99，相比高83.33%。改进粒子群算法由于要进行交叉操作，在运行时间上劣于遗传算法，但在收敛速度、稳定性上好于遗传算法。

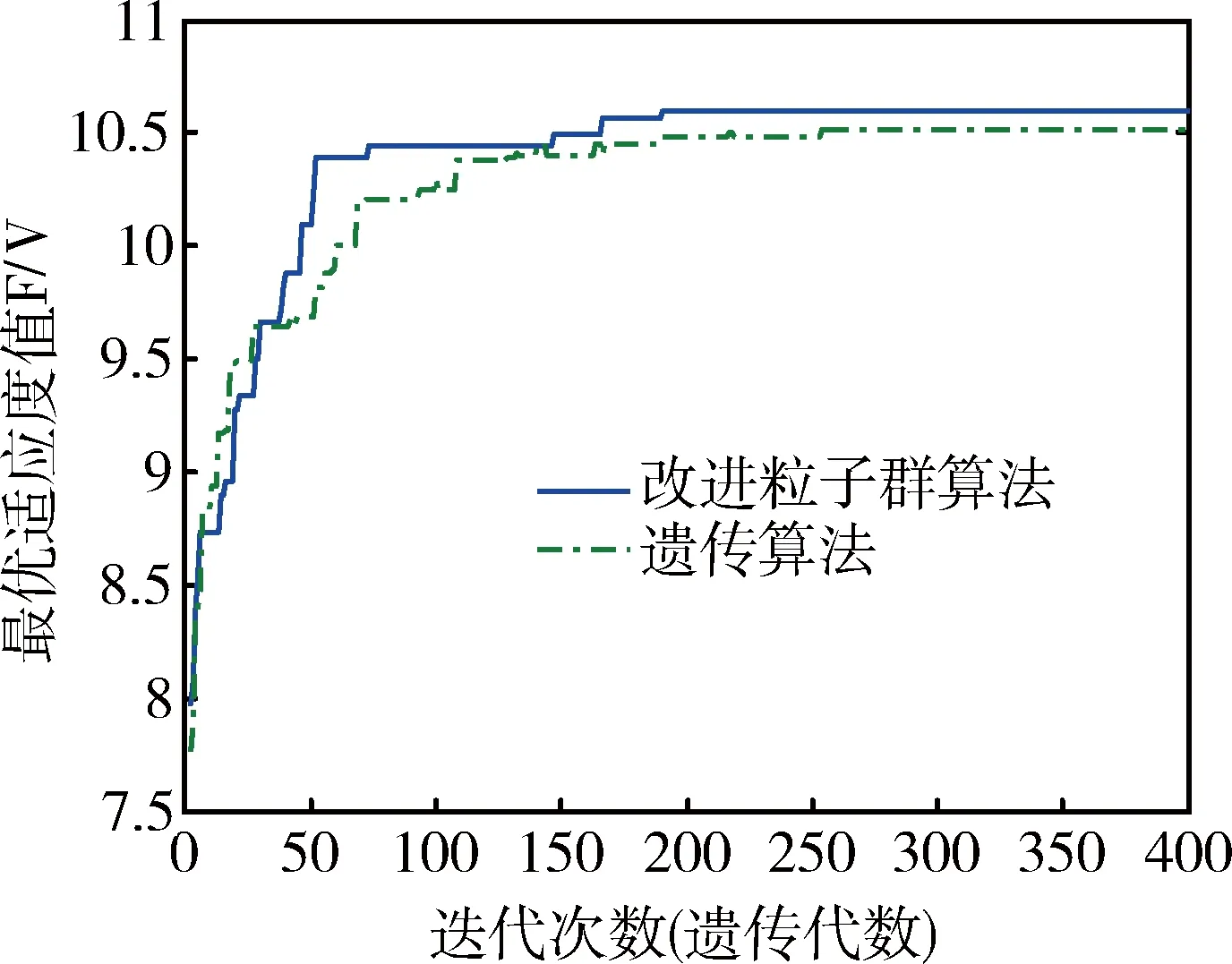
图4 适应度函数F(V)变化曲线(m=n，单次结果)

同理，图5对比了MKV为20个、目标为16个时，改进粒子群算法与遗传算法的结果对比。从图中可以看出在弹目数量不等的情况下，2种算法收敛速度相当，但改进的粒子群算法具有更优的适应度值F，为12.3，相比遗传算法提高了3.4%。将算法连续运行100次得到统计结果为：总运行时间，遗传算法为238.88s，改进粒子群算法为240.03s，基本相当；适应度值F>11.5的次数，改进粒子群算法为100次，遗传算法为86次，相比增加16.27%。通过对比，改进粒子群算法在适应性上也优于遗传算法，在获取更优性能的分配结果上改进粒子群算法具有优势。

图5 适应度函数F(V)变化曲线(m≠n，单次)

5 结论

尝试利用粒子群算法解决多拦截任务分配问题，针对原始粒子群算法容易陷入局部最优，分配效果不佳的问题，本文利用遗传算法的交叉思想对粒子更新策略进行了改进，仿真结果显示，改进后的算法取得了更好的优化结果，与遗传算法相比，改进后的算法具有更强的稳定性，没有出现优化退化问题，在计算量方面，改进算法略大于遗传算法，但是在优化结果上远好于遗传算法，综合计算量和优化效果，改进粒子群算法显示出较好的性能，说明本文选择和设计的优化算法是有效的，具有一定的参考价值，后续将进一步考虑对分配时效性以及目标存在转移等不确定因素下的动态分配策略设计问题。

[1] Rober W. Future Ballistic Missile Interceptor May Carry Dozens of Kill[J]. Aviation Week&Space Technology, 2004, 160(1):50-57.

[2] Matlin Samuel. Review of the Literature on the Missile Allocation Problem[J]. Operations Research. 1970, 18(3):334-373.

[3] 李勇君, 黄卓, 郭波.武器-目标分配问题综述[J]. 兵工自动化, 2009, 28(11): 1-5.(Li Yong-jun, Huang Zhou, Guo Bo. Review of Weapon-Target Assignment Problem[J]. Ordnance Industry Automation, 2009, 28(11):1-5.)

[4] 李俨, 董玉娜.基于SA-DPSO混合优化算法的协同空战火力分配[J].航空学报, 2010, 31(3):626-631. (Li Yan, Dong Yu′na. Weapon-target Assignment Based on Simulated Annealing and Discrete Particle Swarm Optimization in Cooperative Air Combat[J]. Acta Aeronautica Et Astronautica Sinica, 2010,31(3):626-631.)

[5] 顾佼佼, 赵建军, 颜骥, 陈学东.基于MODPSO-GSA的协同空战武器目标分配[J].北京航空航天大学学报, 2015, 41(2):252-268. (Gu Jiaojiao, Zhao Jianjun, Yan Ji, Chen Xuedong. Cooperative Weapon-target Assignment Based on Multi-objective Discrete Particle Swarm Optimization-gravitational Search Algorithm in Air Combat[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(2):252-258.)

[6] 麻士东, 龚光红, 韩亮.目标分配的蚁群-模拟退火算法及其改进[J].系统工程与电子技术, 2011, 33(5): 1182-1186.(Ma Shidong, Gong Guanghong, Han Liang. Hybrid Strategy with Ant Colony and Simulated Annealing Algorithm and Its Improvement in Target Assignment[J]. Systems Engineering and Electronics. 2011,33(5):1182-1186.)

[7] Mehmet A.S, Kemal L. Approximating the Optimal Mapping for Weapon Target Assignment by Fuzzy Reasoning[J]. Elsevier Information Sciences. 2014, 255:30-44.

[8] 张春美, 陈杰, 辛斌.武器目标分配问题的离散差分进化算法[J].北京理工大学学报, 2014,34(3):289-293. (Zhang Chunmei, Chen Jie, Xin Bin. A Discrete Differential Evolution Algorithm for the Weapon Target Assignment Problem[J]. Transaction of Beijing Institute of Technology, 2014, 34(3):289-293.)

[9] Xin B, Chen J, Zhang J. Efficient Decision Makings for Dynamic Weapon-target Assignment by Virtual Permutation and Tabu Search Heuristics[J]. IEEE Transaction on Systems Man, and Cyber-netics.,Part C: Application and Re-views,2010,40(6):649-662.

[10] 刘传波, 丘志明, 吴玲.动态武器目标分配问题的研究现状与展望[J].电光与控制, 2010,17(11):43-48.(Liu Chuanbo, Qiu Zhiming, Wu Ling. Review on Current Status and Prospect of Researches on Dynamic Weapon target Assignment[J]. Electronics Optics & Control, 2010,17(11):43-48.)

[11] 马亚邦.大气层外多拦截器协同反导任务若干问题研究[D]. 哈尔滨工业大学硕士学位论文, 2013:29-37.(Ma Yabang.Study on Antimissile-Cooperation Problems for Exo-Atmospheric Multiple Kill Vehicle[D]. Master Degree Dissertation of Harbin Institute of Technology, 2013:29-37.)

北京航天自动控制研究所牵手曼彻斯特大学共建联合实验室

2016年3月16日，北京航天自动控制研究所与英国曼彻斯特大学在英国签署了中英先进控制系统技术联合实验室合作协议，标志着北京航天自动控制研究所首家海外研发机构正式成立。

自2015年启动联合实验室建设工作以来，在集团和院领导的关怀下，在有关部门和单位的大力支持下，中英双方通过讲学交流和互访等方式增进了解，围绕深化合作进行了多轮次洽谈，对联合实验室的研究方向、运行模式、知识产权归属等进行广泛讨论，并就合作协议达成一致。

据悉，该联合实验室后续将联合开展先进控制技术研发、成果转化和学术交流，同时作为创新人才培养的前沿阵地与窗口，还将联合国内外优势资源，吸纳国际先进智力成果，培养国际化的优秀创新人才，推进多学科的交叉融合，进一步促进航天控制技术的整体发展。(王 森)

The Weapon-Target Assignment Optimal Strategy Based on Particle Swam Algorithm in Multiple Kill Vehicle Interceptor

Li Ruikang1，Shi Bingzheng1, Zhang Zhao2, Jing Wuxing2

1.Shanghai Electro-Mechanical Engineering Institute, Shanghai 201109，China 2.Department of Aerospace Engineering, Harbin Institute of Technology, Harbin 150001，China

Theweapon-targetassignment(WTA)strategyprobleminexoatmosphericinterceptsceneisresearchedtoberesolvedinthispaper.Firstly,theobjectivefunctionisestablished,whichisbasedonthetargetthreatandinterceptioneffectiveness.Then,thetargetassignmentstrategyisdesignedbyusingbasicparticleswarmoptimizationalgorithm.Duetothedrawbacksofbasicparticleswarmalgorithm,animprovedparticleswarmoptimizationalgorithmispresentedbyusingthegeneticcrossovertheory.Finally,theimprovedparticleswarmalgorithmsimulationanalysisisimplemented.Thesimulationresultsdemonstratethattheweaknessofthebasicparticleswarmoptimizationalgorithmisovercomeandtheimprovedoptimizationalgorithmhasbetterperformancebycomparingwiththegeneticalgorithminconvergence,stabilityandadaptability.

Multiplekillvehicle;Targetassignmentstrategy;Geneticalgorithm;Particleswarmalgorithm

2015-06-01

李瑞康(1982-)，男，江西瑞金人，博士，高级工程师，主要研究方向为系统建模、导弹动力学与控制；史秉政(1984-)，男，太原人，工程师，主要研究方向为指挥控制系统；张 召(1989-)，男，河北河间人，硕士研究生，主要研究方向为飞行动力学与控制；荆武兴(1965-)，男，河南鹿邑人，博士生导师，主要从事空间飞行器动力学与控制、系统辨识、非线性制导及自主导航等方面的科研与教学工作。

V448.2

A

1006-3242(2016)02-0066-05

*上海市科学技术委员会资助(13QB1401600)