不同地质条件下边坡动力特征的DDA方法分析
刘 勇,王运生,唐 起,陈怡西
不同地质条件下边坡动力特征的DDA方法分析
刘勇,王运生,唐起,陈怡西
(成都理工大学地质灾害防治与地质环境保护国家重点实验室,成都610059)
为了对边坡动力响应特征进行分析,基于非连续变形分析(DDA)方法,改进了部分程序,并利用改进的DDA建立了边坡分析模型。该模型绘制了坡体中加速度放大系数等值线图,首先验证了模型黏滞边界的远近对边坡动力响应特征影响极小;其次,分析了不同坡角、坡高、岩性及输入一定地震波周期条件下的边坡加速度放大系数等值线随高程及水平深度的变化特征。分析表明:坡角、坡高小于一定值时,加速度放大系数随高程及水平深度增加呈递增趋势,同一边坡岩性较硬或输入波周期较长时,加速度放大系数较大;而当边坡中存在节理及软弱夹层等不利地质体时,地震波传播会受到反射和透射作用的影响,从而影响边坡的动力特征。经DDA模拟计算揭示:当岩体弹性模量较大时,节理对地震波传播的透射作用较强,且当节理间距与输入波长的比值小于临界值时,其比值越大,节理对波的透射作用越强;岩体分界面下部岩性较上部岩性硬时,随着2种岩体弹性模量差值增大,透射波峰值加速度衰减越明显,而反之分界面以下岩体较上部软时,随2种岩体弹性模量差值增大,透射波峰值加速度放大越明显;当软弱夹层厚度以及其与周围岩体波阻抗的比值较大时,地震波经过软弱夹层时的透射作用较小。
边坡;地震波;动力特性;放大系数;软弱夹层;DDA;透射系数
doi:10.11988/ckyyb.20150453
1 研究背景
边坡动力问题一直是岩土工程和地震工程中广为关注的重要问题之一,地震作用下导致的边坡失稳造成的破坏比地震本身作用造成的破坏更严重,因而对地震作用下边坡的动力特征研究显得极为重要。
关于边坡动力问题的研究最早可追溯到1936年,Mononobe等[1]第1次提出并采用了剪切楔法模型研究了边坡的动力特征。目前很多学者通过仪器观测与分析边坡的动力特征,取得了很大的成就,如,国外学者通过仪器对卡格尔山山上和山脚2个点的强余震观测记录中显示:山顶地震持续时间显著增长,放大效应显著,并且位移、速度、加速度3个参量的放大效应不同,位移放大最明显,可达7倍[2];“5·12”汶川地震之后,青川东山、泸定冷竹关、摩岗岭及绵竹九龙剖面的余震监测数据也表明[3-4]山顶地震波加速度较山脚放大效应明显,坡顶同一监测点水平分量不同方向的峰值加速度相差较大;沿单薄山脊走向的地震波峰值加速度小于垂直单薄山脊的地震波峰值加速度。刘汉香等[5]通过大型振动模型试验也揭示:同种地震波及等强度作用下,合成向、水平x向(纵向)和竖直z向对斜坡的变形影响依次加强。
目前的研究大多针对斜坡表面及斜坡浅表层,对斜坡深层部位的节理及软弱夹层等不利地质体研究较少。近年来的研究发现边坡中的不利地质体对边坡的动力特征影响较大,但其具体影响特征目前尚不完全清楚。在前人研究的基础上,本文通过对非连续变形分析(DDA)方法进行改进,将其用于边坡的动力响应特征分析,通过大量的数值模拟计算,分析了边坡形态、输入波周期及不利地质体等对边坡动力特征的影响。
2 非连续变形分析(DDA)方法基本理论
DDA方法是平行于有限元法的一种数值分析方法,与有限元法不同的地方在于它以计算不连续面的滑移、开裂和旋转等大位移的静力和动力问题。该方法的基本理论是[6]:计算几何模型由节理等结构面切割而形成的块体单元组成;块体单元的运动和变形由切向应变、法相应变、位移和转动组成,DDA方法以各块体单元的位移量为未知量;块体运动过程中各单元之间可以接触,也可以分离,但必须满足库仑准则和块体间无嵌入、无拉伸条件;结合边界条件,通过最小势能原理把块体间的接触问题和块体本身的变形问题统一到矩阵中求解,得出总体平衡方程;采用基于时步的隐式方法求解方程组也可得出块体系统平衡时的位移场、应力场等,还可以得出各块体在运动过程中的相对位置和接触关系。该方法自1986年提出后,在国内外岩土工程界受到广泛关注,其有效性也已被国内外学者所证明[7]。
3 边坡动力响应特征的数值分析
为分析边坡形态及输入波对其动力特征的影响,假定边坡为均质岩性,不考虑节理、软弱夹层及水的影响,在坡内各块体中设置监测点,以分析整个边坡中各个部位动力响应特征的变化,提取各监测点在整个计算时程中的加速度峰值,定义任意一点加速度峰值与坡脚处加速度峰值的比值为地震波的放大系数,并在坡体内绘制放大系数的等值线图。
3.1不同坡形下边坡的动力响应规律分析
通过坡高和坡角来分析坡形对边坡动力特征的影响。图1为坡脚35°,坡高分别为30,60,150 m,
图1不同坡高下边坡动力响应特征
(加速度放大系数等值线)
Fig.1Dynamic response characteristics of slope with different slope heights岩性弹性模量为5.4×103MPa,泊松比为0.21,输入波特征周期T为0.2 s的加速度放大系数等值线图。从图1中可以看出,坡高较低时,加速度放大系数随高程和水平深度呈递增趋势,其等值线在剖面上近等间距分布,到达坡肩转折处向坡体内部等值线逐渐变稀疏;随着坡高增大,达150 m时,在高程约80 m处坡体内部形成一个较大的加速度极大值中心,该高程以下加速度放大系数随高程和水平深度仍呈递增趋势,超过该高程后加速度随高程递减,在水平方向上随水平深度增加,加速度也不再继续增大,而是呈现时而增大、时而减小的节律性变化。
图2是坡高为60 m,坡角为40°,50°,60°,坡体弹性模量为5.4×103MPa,泊松比为0.21,输入波特征周期 T为0.2 s的加速度放大系数等值线图。从图1(b)和图2中可以看出坡角较小时(不超过50°)坡体中的加速度放大系数等值线分布形式基本相同,在剖面上近等间距分布,从坡肩转折处向坡体内部逐渐变稀疏,随坡角增大加速度放大系数增加;当坡角增大达60°时,坡面处的加速度放大系数不再随高程线性增加,而是时而增大,时而减小的节律性变化,且在坡体内形成一个极大值中心,坡面附近也会出现一些较小的圈闭区域,随着坡角增大,较小的圈闭区域数量增多。
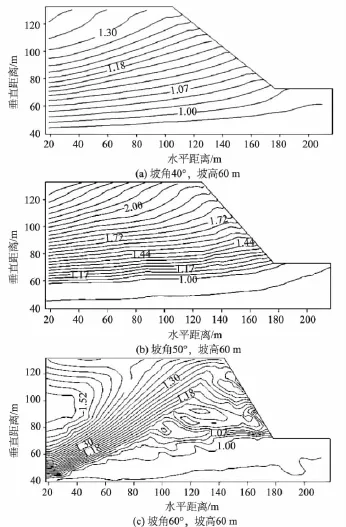
图2 不同坡角下边坡的动力响应特征(加速度放大系数等值线)Fig.2 Dynamic response characteristics of slope with different slope angles
不同坡形下边坡的动力特征不同主要与地震波传入岩体后产生的释能体范围有关,斜坡岩体在地震波传入后会出现一定范围的弹性变形,而发生弹性变形的岩体都会产生回弹(弹性回跳)释放能量,并形成以坡面为轴面的释能体,释能体的空间方位和大小决定振动影响场的大小和形状,因而导致不同坡形下地震波的不同放大。在现实调查过程中,边坡坡高大多不超过150 m,坡角不超过50°,地震作用下边坡加速度随高程、水平深度及坡角增加,因而在高程较高或坡角较大时最易失稳,在对其防治过程中加速度放大系数较大部位的抗震安全系数应设置较大。
3.2不同岩性下边坡的动力响应特征分析
图3是坡高为60 m,坡角为40°,泊松比为0.21,输入波特征周期T为0.2 s,岩体弹性模量为2×103MPa的加速度放大系数等值线分布图。从图3和图2(a)(弹性模量为5.4×103MPa)比较可以看出,同一边坡,岩性较软的坡体和较硬的坡体加速度放大系数等值线分布形式基本相同,较软的岩质边坡比较硬的岩质边坡放大系数增加幅值小,即同一坡形面若岩质较硬时,边坡加速度放大系数较大。地震波在岩体中传播,能量逐渐减小,当传播过程中的介质弹性模量大时,地震波能量衰减较少,故相同坡形下岩质较硬的边坡加速度较大,因此在边坡防治过程中应考虑岩体的硬度,可适当降低软岩地区边坡安全系数。
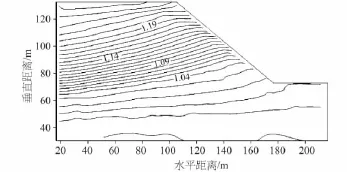
图3 弹性模量为2×103MPa下边坡的动力响应特征(加速度放大系数等值线)Fig.3 Dynamic response characteristics of slope with elastic modulus of 2×103MPa
3.3输入波周期不同时边坡的动力响应特征分析
图4是坡高为60 m,坡角为40°,坡体弹性模量为5.4×103MPa,泊松比为0.21,输入波特征周期T为0.5 s的边坡动力响应的加速度放大系数等值线分布图。从图4和图2(a)(输入波周期为0.2 s)比较中可以看出,同一边坡不同周期的地震波输入,加速度

图4 输入波周期0.5 s下边坡的动力响应(加速度放大系数等值线)Fig.4 Dynamic response characteristics of slope with input wave period of 0.5s
放大系数等值线的分布形式基本相同;输入波周期增长时,加速度放大系数增加幅值增大,即同一坡形面若输入周期较长的地震波时,加速度放大系数变大。在相同介质中,正弦波的周期较长时,波长越长,在传播过程中受到的干扰越小,波的能量损失越少。故传入的地震波周期较长时,边坡加速度越大,也最易失稳。因而在边坡抗震稳定性评价过程中,应考虑该地区可能发生的地震波最长周期。
3.4不利地质结构对边坡动力特征的影响
3.4.1节理对地震波传播的影响
当坡体中有节理出现分界面时,地震波传播经过节理面会出现反射及透射,从而影响边坡的动力响应特征。定义节理面两侧透射波与入射波的峰值加速度的比值为地震波经过节理面的透射系数,即:α= T'/T,其中:α为透射系数,T'为地震波穿过节理面后的透射波峰值加速度,T为入射波的峰值加速度。
蔡军刚等[8]、张勇慧等[9]提出节理间距会影响地震波的传播,文中采用DDA建立概化模型分析节理间距及岩性刚度对地震波传播规律的影响,建立长200 m,宽100 m的模型如图5,模型材料弹性模量为5.4×103MPa,泊松比为0.21,密度为 2 600 kg/m3,不计重力。模型中设置2条真实节理,并在底部和顶部设置测点以监测入射波和透射波的变化,设置虚节理细分模型(单元块体尺寸为5 m× 5 m),虚节理参数设置较大以保证块体的连续性,

图5 节理面分析模型Fig.5 Analysis model of joint surface
廖振鹏[11]通过对分界面上的应力及位移的连续条件进行分析,推导出了弹性波在分界面上的透射和反射系数公式分别为:模型两侧及底部边界依然采用黏滞边界条件,在底部输入周期为0.2 s的正弦波。
Schoenberg等[10]根据弹性理论也推导出了弹性波垂直入射单个节理面的透射系数,即
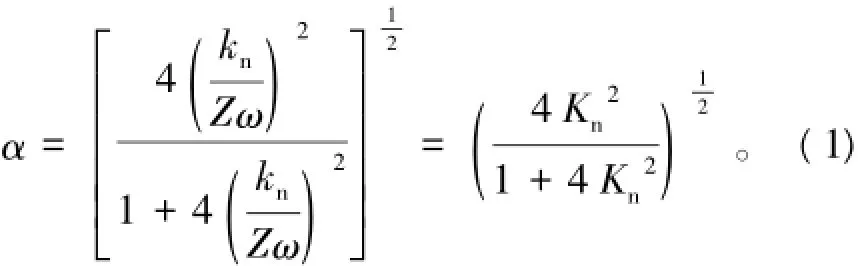
在图5节理面模型中先设置一条真实节理,通过改变模型的弹性模量,计算不同弹性模量下节理面的透射系数,并将其与理论公式(式(1))计算值比较,以验证DDA模拟节理对地震波传播的影响是否合理。表1为数值模拟值与理论公式计算值的对比。

表1 节理面透射系数模拟值与理论值对比Table 1 Comparison of transmission coefficient at joint surface between simulated results and theoretical results
从表1中可以看出,DDA模拟值与理论值误差较小,最大为4.49%,故采用DDA模拟节理面对地震波传播的影响是合理的;通过计算不同弹性模量下的透射系数,可以发现,随着岩性弹性模量增大,地震波的透射系数增加,即越硬的岩体节理面对地震波的反射作用越弱,透射作用越强。因而在硬岩边坡中,节理面对边坡的动力响应特征影响较小。在图5模型中改变2条节理间的间距来模拟节理间距对透射系数的影响,其结果如图6所示。从图6中可以看出,节理间距<35 m时,随间距增加透射系数增大;当节理间距>35 m时,透射系数随节理间距成递减趋势;当节理间距>60 m时,随间距增大地震波的透射系数基本不再变化。根据Schoenberg等[10]的研究,节理间距对透射系数的影响与入射波的波长也有关系,根据入射波特征周期算出入射波长为305.8 m。从图6中可知,透射系数达到峰值时的节理间距为33.6 m与入射波长的比值γ=0.11时,透射系数达到临界值;渗透系数不再随节理间距明显变化时的阀值61 m与入射波长的比值γ=0.20时,透射系数达到阀值;节理间距与波长比值γ<0.11时,透射系数与γ近似正相关,0.2>γ>0.11时,透射系数与γ呈递减趋势,γ达到阀值后,透射系数基本不在变化。因此,当节理间距与波长比值较小时,地震波的透射系数较小,对边坡动力响应特征影响较大;γ达到临界值时,透射系数最大,对边坡动力响应特征影响最小。
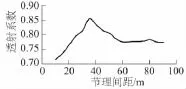
图6 透射系数与节理间距的关系Fig.6 Relationship between transmission coefficient and joint spacing
3.4.2软弱夹层对地震波传播的影响
当坡体中出现软弱夹层时,岩体整体性受到破坏,出现不同介质分界面,地震波的传播会受到影响,为了简化计算,本次只计算一层软弱夹层的影响。首先采用DDA方法模拟地震波在不同介质分界面上的传播规律,建立模型如图 7所示,模型长200 m,宽100 m,模型上部岩性的弹性模量为5.4×103MPa,泊松比为0.21,密度为2 600 kg/m3,不计重力。通过改变分界面以下岩性的弹性模量来计算不同分界面对地震波透射系数的影响,并将数值模拟值与理论公式计算值比较以验证DDA对分界面的模拟是否合理。在模型底部输入周期为0.2 s的正弦波,模型两侧及底部依然采用黏滞边界。

图7 不同介质分界面模型Fig.7 Interface model for different materials
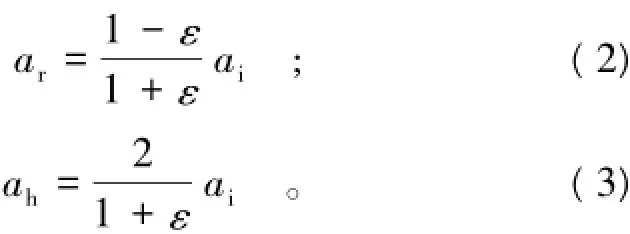
从表2中数据可以看出,DDA计算值与理论公

表2 分界面透射系数模拟值与理论值对比Table 2 Comparison of transmission coefficient at interface between simulated results and theoretical results
式计算值误差较小,故采用DDA对地震波经过分界面透射系数的计算是合理的。当分界面下部岩性较上部岩性硬时,地震波在经过分界面时其峰值加速度会降低,随着2种岩性弹性模量差别增大,地震波峰值加速度降低越明显;分界面以下岩性较上部软时,地震波经过分界面时,其加速度峰值会增大,且随2种岩性弹性模量差值越大,加速度放大越明显。
岩体中存在软弱夹层时,地震波传播会遇到多个分界面。分界面上产生的反射波与入射波会出现干涉现象,从而影响地震波经过软弱夹层时的透射系数,其干涉现象的强弱与软弱夹层的厚度有关。建立模型如图8所示,模型长200 m,宽100 m,模型岩性的弹性模量为10×103MPa,泊松比为0.21,密度为2 600 kg/m3,软弱夹层的弹性模量为1×102MPa,泊松比为0.21,密度为2 600 kg/m3,模型底部输入周期为0.2 s的正弦波,两端及底部依然采用粘滞边界。
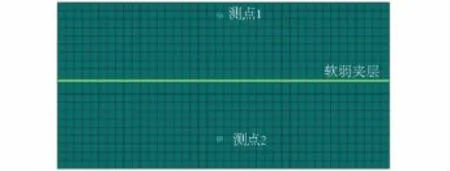
图8 软弱夹层分析模型Fig.8 Analysis model of weak interlayer
变化软弱夹层的厚度,计算不同厚度下的透射系数,模拟计算结果如图9(a)。从图9(a)可以看出,软弱夹层厚度减小时,透射系数增大明显,这主要与随厚度减小分界面上多重反射效应越来越强有关;当厚度达到8 m时,透射系数基本不再变化,根据输入波长,可以求出软弱夹层厚度与波长比值约达0.03时,其透射系数不再随厚度增加而变化。
式(2)和式(3)求分界面反射波和透射波的峰值加速度公式与上下介质的波阻抗比也有关系,其影响规律可以利用DDA通过改变软弱夹层的弹性模量来模拟不同波阻抗比对软弱夹层透射系数的影响。在图8模型中设置软弱夹层的厚度为3 m,变化软弱夹层的弹性模量(改变软弱夹层与周围岩性的波阻抗比),其他参数不变,透射系数的计算结果如图9(b)所示。从图9(b)中可以看出,当波阻抗比<0.38时,随波阻抗比增加,透射系数下降明显;当波阻抗比超过0.38时,透射系数随波阻抗比依然呈递减趋势,但下降不再明显。因此,当软弱夹层厚度以及其与周围岩体波阻抗比较大时,波经过软弱夹层的透射系数较小,对边坡的动力特征影响较大。

图9 透射系数与软弱夹层厚度、波阻抗比的关系Fig.9 Relation of thickness of weak interlayer and acoustic impedance ratio vs.transmission coefficient
4结论
文中对DDA地震波输入方式与人工边界条件进行了改进,并验证了其改进的合理性,将其用于边坡动力响应特征分析,模拟了边坡形态、输入波周期及不利地质体等对边坡动力特征的影响。得出的主要结论如下:
(1)当坡角一定,坡高较低时,加速度放大系数随高程和水平深度递增;坡高增加到一定值时,加速度放大系数不再随高程增加,而是呈现先增大,到达极大值中心后又递减的趋势,加速度放大系数也不再随水平深度递增,而是呈现节律性变化。坡高一定时,加速度放大系数随坡角变大;当坡角增大到一定值时,坡面处的加速度放大系数不再随坡角递增。
(2)边坡岩质较硬或传入的地震波周期较长时,坡面处加速度放大系数较大;当岩体中存在节理面时,岩体弹性模量越大,节理面对弹性波的透射作用越强,反射作用越弱;当节理间距与波长比值较小时,地震波的透射系数较小,对边坡动力响应特征影响较大,其比值达到临界值时,透射系数最大,对边坡动力响应特征影响最小。
(3)边坡中存在不同物理力学性质的岩性分界面时,若分界面下部岩性较上部岩性硬,则随着2种岩性弹性模量差别增大,透射波峰值加速度降低越明显;反之当分界面以下岩性较上部软时,随2种岩性弹性模量差值增大,透射波峰值加速度放大越明显;若存在软弱夹层时,软弱夹层厚度以及其与周围岩体波阻抗的比值越大,地震波经过软弱夹层时的透射作用越小。
文中探讨了节理、岩性分界面及软弱夹层等不利地质体对地震波传播的影响。通过对地震波经过节理等不利地质体的放大特性分析,有助于地震作用下滑坡失稳机制的研究,并能为滑坡防治提供必要的依据。但地震作用下,不利地质体对地震波放大的定量化还未实现,仍需要进一步研究。
[1] GAZETAS G.Seismic Response of Earth Dams:Some Recent Developments[J].Soil Dynamics&Earthquake Engineering,1987,6(1):2-47.
[2] 张倬元,王士天,王兰生,等.工程地质分析原理[M].北京:地质出版社,2009:181-182.
[3] 罗永红,王运生.汶川地震诱发山地斜坡震动的地形放大效应[J].山地学报,2013,31(2):200-210.
[4] 罗永红.地震作用下复杂斜坡响应规律研究[D].成都:成都理工大学,2011.
[5] 刘汉香,许强,徐鸿彪,等.斜坡动力变形破坏特征的振动台实验模型研究[J].岩土力学,2011,32(增刊2):334-339.
[6] 付晓东,盛谦,张勇慧.开挖及动荷载作用下边坡响应的DDA方法研究[J].岩石力学与工程学报,2012,31(增刊1):2612-2618.
[7] MACLAUGHLIN M M,DOOLIN D M.Review of Validation of the Discontinuous Deformation Analysis(DDA)Method[J].International Journal for Numerical and Analytical Methods in Geomechanics,2006,30(4):271-305.
[8]CAI J G,ZHAO J.Effects of Multiple Parallel Fractures on Apparent Attenuation of Stress Waves in Rock Masses[J].International Journal of Rock Mechanics and Mining Sciences,2000,37(4):661-682.
[9] 张勇慧,付晓东,盛谦.基于DDA方法的不利地质结构对弹性纵波传播规律的影响研究[J].四川大学学报(工程科学版),2012,44(5):86-92.
[10]SCHOENBERG M.Elastic Wave Behavior Across Linear Slip Interfaces[J].Journal of Acoustical Society of America,1980,68(5):1516-1521.
[11]廖振鹏.工程波动理论导论[M].北京:科学出版社,2002.
[12]CHENG X L,MIAO Q H,WANG Y,et al.Design and Implementation of Software Architecture for DDA[C]∥ISRM Commission on Discontinuous Deformation Analysis.Proceedings of the 11th International Conference on Analysis of Discontinuous Deformation.Fukuoka,Japan,August 27-29,2013:147-152.
(编辑:姜小兰)
Discontinuous Deformation Analysis of Slope Dynamic Characteristics under Different Geological Conditions
LIU Yong,WANG Yun-sheng,TANG Qi,CHEN Yi-xi
(State Key Laboratory of Geohazad Prevention and Geoenvironment Protection,Chengdu University of Technology,Chengdu610059,China)
In order to analyze the dynamic response of slope,we establish a slope analysis model by using improved DDA(discontinuous deformation analysis),and obtain contours of acceleration amplification coefficient in slope body.First of all,we verify that viscous boundary distance has minimal effect on dynamic response characteristics of slope.Secondly,we analyze the changes of amplification coefficient with elevation and depth in the presence of different slope angles,slope heights,lithology,periods of seismic wave,etc.Analysis shows that,1)if slope angle or slope height is smaller than a certain value,amplification coefficient increases with elevation and depth;2)harder rock or longer period of input wave will lead to bigger amplification coefficient;3)in case of adverse geological bodies such as joint and weak interlayer,seismic wave propagation will be influenced by reflection and transmission,thus affecting dynamic response characteristics of slope.On the basis of DDA,we can find the following results.Big elastic modulus is in favor of transmission effect of joint on wave propagation.When the ratio of joint spacing to input wave length is smaller than critical value,the greater the ratio is,the stronger the effect of joint on transmission wave is.If rock under interface is harder than that above the interface,and when the difference between two elastic modulus increases,the reduction of peak acceleration in transmission wave gradually tends to be obvious.On the contrary,the reduction will be changed into amplification.When weak interlayer thickness or ratio of the thickness to acoustic impedance in surrounding rock is bigger,transmission effect of seismic wave through weak interlayer is smaller.
slope;seismic wave;dynamic characteristics;amplification coefficient;weak interlayer;DDA;transmission coefficient
P642.2
A
1001-5485(2016)07-0115-06
2015-06-01;
2015-07-16
中国地质调查项目(12120113010100)
刘勇(1989-),男,四川广元人,硕士研究生,主要从事地质工程专业方面的研究,(电话)18482176120(电子信箱)1039786137@ qq.com。

