沪深300指数成分股系统性风险贡献分析
——基于股票指标关联网络的研究
乔海曙 ,杨蕾
(湖南大学金融与统计学院,湖南长沙,410082)
沪深300指数成分股系统性风险贡献分析
——基于股票指标关联网络的研究
乔海曙 ,杨蕾
(湖南大学金融与统计学院,湖南长沙,410082)
以沪深300指数成分股为节点构建股票关联网络,运用CoVaR方法测度各成分股对整体市场的系统性风险贡献度,研究个股在股市中关联度的大小与其系统性风险的关系。结果发现,在股票关联网络中处于核心位置的股票,其系统性风险贡献度越高。说明在股票市场中,关联度越广的上市公司,其传导危机的可能性越高,对系统性风险的贡献度越大。在系统性风险监督防范的过程中,应该对市场中关联度广、影响力强的公司给予更高的关注。
系统性风险;股票关联性;复杂网络;CoVaR方法
一、引言
全球经济金融一体化大背景下,世界各国证券市场之间边界逐渐模糊,任意国家或地区产生的风险都有可能呈现出较强的传染性。近年来,相继爆发的多次金融危机都显示与证券市场上系统性风险的传染有关,系统性风险的起因和防控逐渐成为众多学者和机构研究的重点。目前国际上关于系统性风险并没有一个统一、权威的定义,但大部分定义中都强调了系统性风险的传染性与破坏性[1-3]。
作为还在不断发展中的新兴市场,我国股票市场的系统性风险也不容忽视,仅2015年6月至今,我国A股市场就已经经历了三次大幅暴跌。与发达市场相比,我国市场机制的完备程度、法规的健全程度以及投资者的成熟程度都存在较大差距,投机之风盛行,呈现出较为严重的“同涨同跌”现象。股票之间的这种高度关联性意味着较高的风险相依性,甚至可能引发较大的系统性风险。具体表现为,某只股票的异常波动可能波及同行业的股票,导致行业内部系统性风险的产生,并存在进一步传染至整个市场,影响股票市场稳定性的可能。因此,从股票间关联度的角度研究股市系统性风险具有重要的现实意义。
本文的研究主要聚焦于以下问题:在整个股票市 场中,关联关系越广,关联度越高的股票,其系统性风险贡献度是不是越大,也就是说,一旦这类股票陷入异常波动,是否会导致更高的系统性风险?因此,本文以沪深300指数成分股作为样本,创新性地通过构建股票关联网络、分析拓扑性质得到各只股票在系统中的关联度,并利用CoVaR方法测度个股对整体的系统性风险贡献度,通过研究在股票网络中处于中心地位的股票是否具备更高的风险贡献度来验证本文的观点。本文的研究是对关联度与系统性风险相关理论研究的补充,将之前集中于金融机构和金融市场间的研究拓展到股票市场内部。基于关联度视角分析股票市场内部系统性风险,分析个股间的关联度与系统性风险的关系,有助于更好地对股市系统性风险进行管理,为正常时期监管措施的采取和危机时期救助措施的实施提供有益参考,有助于维护股票市场的健康有序运行。
二、系统性风险相关文献综述
深入了解系统性风险是防范系统性风险的重要前提,国内外学者已经对此进行了大量研究,目前主要集中于系统性风险的测度和传染两方面。国外对证券市场系统性风险测度的研究较为丰富,从1952年“均值-方差”理论的提出,以及在此基础上诞生的资本资产定价模型 CAPM,使用 β值衡量证券系统性风 险[4],到Baumol W.提出的VaR模型[5],早期的系统性风险测度方法都未考虑资产之间的风险溢出,存在一定的局限性。不少学者开始寻找新的方法进行风险测算,Adran和Brunnermeier创新性地运用CoVaR方法对系统性风险进行度量,研究某一金融机构或金融市场陷入风险状态时对其他金融机构或金融市场的影响[6],目前已经成为系统性风险测度的重要方法,并在系统性风险传染的研究中得到了较为广泛的应用。
传染性是系统性风险的重要特性,而金融体系内部的关联度及其变化则是系统性风险传染的主要载体。关于关联度与系统性风险传染的研究,目前主要集中于金融市场及金融机构层面。不少学者对金融市场间的风险关联进行了研究,柏满迎等对我国股票市场和基金市场间的风险溢出关系进行了研究,发现沪深股市与基金市场间具有紧密的联动关系[7],费兆奇对股市波动传递的一体化和传染现象进行了研究,发现股票市场的国际一体化水平具有时变特征[8]。梁琪等则运用复杂网络和溢出指数等方法对国际股票市场间的联动关系和风险传导进行了研究,发现股市一体化的提高并不必然伴随着风险联动的增强[9]。金融机构间的风险传染也是学者们研究的重点,不少学者认为金融机构之间错综复杂的业务关系[10]以及资产负债关系[11]为系统性风险的传播提供了传播渠道,Gal对高集中度的网络结构进行了研究,发现系统关联度高时更容易发生系统性风险传染[12]。范小云等运用CCA和 DAC方法对我国银行系统性风险进行了研究,发现处于风险传染网络中心的银行具有更高的系统重要性[13]。陈忠阳和刘志洋在上市银行系统性风险贡献度的基础上,验证了银行间的关联度与系统性风险之间的联系[14]。隋聪等通过构建银行间网络,发现在集中度高的网络中风险传染的可能性更高[15]。
通过文献梳理发现,关于系统性风险的研究,主要包括系统性风险的测度以及传播两方面。随着国际股票市场间联动关系的日益密切以及相关研究的深入,系统性风险的测度方法不断更新,对系统性风险传染性的研究也逐渐成为研究的重点,目前基本上集中于金融市场或金融机构层面。众多研究表明,不同金融市场或不同金融机构间的关联度与其系统性风险传染密切相关。但目前关于证券市场内部,个股间的关联度与系统性风险之间关系的研究还比较少。因此,本文拟从证券市场内部关联的角度出发,考虑个股间的相关性风险,研究市场内部关联性对证券市场整体系统性风险的影响。
三、理论基础与研究假设
传统金融理论,主要基于“有效市场假说”和“理性人假说”,视资本市场投资者为同质的风险厌恶者,较少关注投资者行为偏好这一重要因素,更未考虑这一因素对证券价格的影响。从文献回顾中也发现,尽管学者们对金融市场间的价格联动与传染现象十分关注,但很少对同一市场内不同证券间的相互关联与影响进行研究,也忽视了这种证券间的关联关系对市场风险特征的影响。
(一) 行为金融学视角下的股票关联
证券市场上,各个公司的证券之间存在一定的关联关系,导致个股之间价格的连锁反应,并可能形成明显的长期同步变动趋势,这种现象一般称之为股价联动。在传统金融学中,主要是从宏观经济状况以及公司基本面等角度对此进行分析。随着行为金融学的兴起,一些学者开始从投资者行为的角度,分析不同证券之间的价格传导效应,为研究证券市场内部关联关系奠定了基础。
从理论上来说,一方面,由于宏观经济、行业因素以及竞争关系等因素的影响,市场中各公司之间存在一定的联系,某家公司证券价格的波动可能会反映出一定的信息,导致其他公司证券价格的变化;另一方面,在信息不完全的条件下,投资者并非完全理性。在证券交易过程中,投资者的理念与行为很容易受到他人的影响,一旦市场中某一证券价格发生变化,投资者会怀疑波动的原因是自己所未知的某种信息,因此往往会参照他人的投资决策进行交易,而非进行理性投资。在某些舆论信息的引导下,大量投资者可能会在某一时段进行相同的操作。投资者的这种行为模式会引发证券需求和价格的变动,使证券市场中某一证券所遭受的风险冲击其他证券,形成个股联动现象。证券之间的关联性和波动的趋同性,为系统性风险的传播提供了渠道,对市场稳定构成威胁。
(二) 股票关联与系统性风险
根据个股联动范围的不同,可以划分为两个层面。一是板块层面的联动,这种联动是基于某种特定关系产生的,比如行业关系、地域关系或某些“概念关系”,属于局部联动。在某一段时间中,特定板块内的股票价格呈现相同的变动趋势。二是市场层面的联动,这种联动是基于共同冲击,表现为市场整体的“同涨同跌”,形成了较大的系统性风险。我国证券市场上,板块层面和市场层面的股票联动现象都非常明显,Jin和Myers对40个国家的股价同步性进行了研究,发现我国股价波动同步性排在第一位[16]。众多国内学者也对这一问题进行了研究,观察和实证都表明,我国证券市场内部关联性较强,各股票价格波动方向具有高度的一致性。
1. 关联关系的紧密性与系统性风险
股票之间高度关联的直接后果就是风险的高度相依性。虽然股票之间的关联性可以在市场出现正面信息时相互影响,使不同股票共同分享系统性的机会,推动市场价格的持续上升。但是一旦市场中出现负面信息,由于股票之间高度关联,任意股票A陷入风险状态,都可能导致投资者预期和资产配置行为的变动,对相关股票甚至整个市场产生影响。一方面,投资者对与股票A有共同点,如行业相似、经营状况相似、“概念”相似的股票产生一致性预期,出于规避风险的目的抛售该类型股票,导致风险的传递;另一方面,股价的波动引发市场中恐慌心理,投资者纷纷抛售股票,这种非理性行为导致了风险的进一步扩散。由此,整个证券市场都可能由于股票之间的关联关系而面临系统性风险。我国股票市场中存在明显的风险关联性,这种风险关联性无疑会增加证券市场的脆弱性,从而导致系统性风险的产生。
2. 关联关系的时变性与系统性风险
股票之间关联度的时变特征,也对系统性风险的产生和传播有着不容忽视的影响。在传统的金融理论中通常假定资产相关系数稳定,而实际上不断有研究发现各种资产或各个市场之间的相关关系具有时变性。Longin和Solnik对国际资本市场相关性结构的变化进行了研究,发现在高波动率期间,市场相关性增加[17]。Ang和Chen也发现,在市场下跌阶段,股票与市场间的相关性比市场上涨阶段要高[18]。Pollet 和 Wilson用模型证明了市场相关性所带来的系统风险是不可忽略的[19]。郑振龙等在此基础上证明了股票与债券市场的平均相关系数可以作为系统性风险的代理指标[20]。从理论上来看,金融资产收益率的相关性分布在尾部和中间是不同的,呈现出一种非线性的相关结构。也就是说,在极端收益的情况下,证券之间的相关性会发生变化。一般来说,极端下跌情况下的相关性会高于上涨阶段的相关性。当一个市场遭受冲击而发生剧烈动荡时,市场中的大多数股票往往都会随之一起暴跌,这就属于一种极端情况下的市场风险,即极端下跌市场风险,其严重程度要远比上涨风险更强。这种相关关系的时变性也是系统性风险的重要来源。
(三) 股票关联与系统性风险研究假设
股票之间的关联性与证券市场系统性风险有着紧密的联系,由于股票市场过度联动以及关联性时变特征的存在,一些公众性突发事件或某行业内关键公司发生的危机都可能会导致整个国内金融市场的波动。本文通过构建股票指标关联网络来把握市场中股票之间的关联程度,在此基础上验证这些股票指标关联性与系统性风险贡献度之间的相关关系。考虑到各种股票指标的性质和指向,选择股票价格、成交量和市盈率等指标进行股票关联网络的构建。股票价格、成交量与市盈率都是反映股票行情的重要指标,与股票市场波动以及投资者行为有着直接或间接的关系,根据前文的理论描述,股票价格作为上市公司经营状况和风险水平的直接反映,是市场中投资者最为关注的指标之一。股价波动的一致性,意味着“板块联动”甚至“同涨同跌”现象的产生,越高的股价关联度,代表着股票之间越高的风险相依性,会引致较大的系统性风险,因此,提出以下假设:
H1:股价波动关联度指标与系统性风险贡献度正相关。
成交量反映了个股交易的活跃程度,对股市行情的变化起到了较为重要的作用,成交量的增减变化与股票价格的涨跌有着较为密切的联系。当市场中信息变化时,都会直接体现在股票成交量和价格指标中,因此,也有学者将成交量作为信息流的替代指标。股票成交量之间关联性越高,代表着股票之间行情变动的联动关系越强,并在一定程度上反映了投资者对这些股票相似的投资行为偏好,会选择在相同时间段对该类股票进行相同操作,可能引发系统性风险。因此,提出以下假设:
H2:成交量关联度指标与系统性风险贡献度正相关。
市盈率作为将股价与收益联系起来的指标,常用于反映股票的投资价值,不少投资者以市盈率作为估计上市公司发展前景的指标,在投资操作中考虑市盈率的影响,偏好于投资达到某一类市盈率水平的股票。因此,股票市盈率指标的高度关联性,不仅反映了上市公司基本面信息的相关关系,也会对投资者行为产生影响,引发市场中的股价联动,导致更高的系统性风险。据此,提出以下假设:
H3:市盈率关联度指标与系统性风险贡献度正 相关。
通过对以上假设的验证,可以证明股票关联度与其系统性风险贡献度之间的联系,并分析股票关联网络中的指标对系统性风险的预警作用。
四、研究方法说明
(一) 运用CoVaR方法计算系统性风险贡献度
1. CoVaR相关理论
Adrian和Brunnermeier[6]在VaR方法的基础上,提出了CoVaR条件风险价值模型。它表示在一定置信水平下,如果某一资产在某一特定时间的损失达到VaR水平时,其他资产的最大可能损失。也就是说,CoVaR也是一种特定情形下的VaR,可以用于计算单个资产对整体的系统性风险溢出,即本文所述的系统性风险贡献度的表示方法如下:
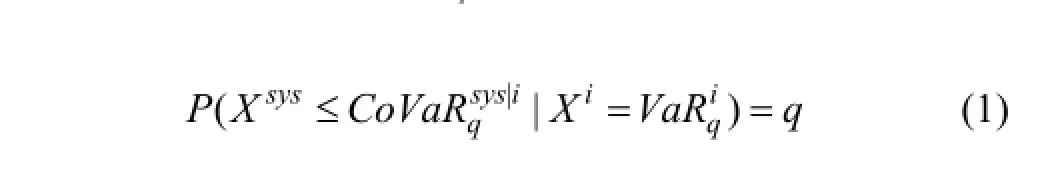
在本文中,为研究我国股票市场中某一股票出现 危机时整个股票系统的风险水平,将上式中的视为某单一股票的风险价值,视为整个股票市场在某一股票处于状态时的条件风险价值,也 就是股票市场某一个体出现危机时,整个系统的总体风险价值。其中,单一股票对整个系统的风险贡献度,应该是总体风险价值减去股票市场的风险价值,即用 某一股票处于危机状态时市场的CoVaR减去所有个体都正常时市场的,可以表示为:可用于衡量某单一股票对整个股票市场的系统性风险贡献度。为了求得,首先需要对进行求解。
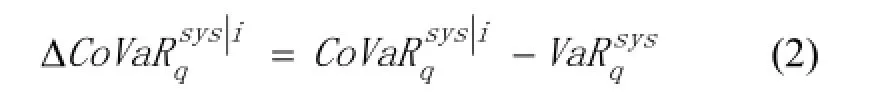
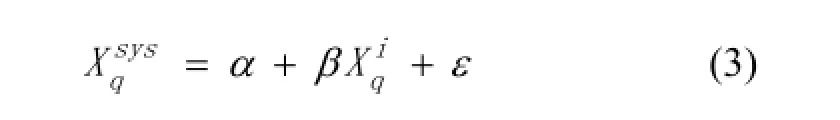
其次,通过式(3)的估计结果,可以计算出股票市场的风险价值估计值。由于在分位数回归中,得到的估计结果就是sysqX对应的q分位数估计值。因此,表达式如下:
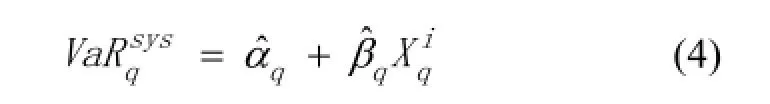
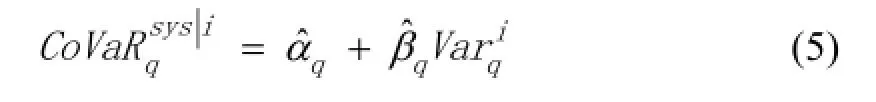
(二) 构建股票关联网络计算股票关联度
1. 复杂网络理论的应用
为了分析股票市场的价格联动现象,并验证股票指标关联程度与系统性风险的相关关系,首先需要采取合适的方法得到股票之间的关联度。市场中股票市场行情瞬息万变,股票价格波动及其关联关系难以把握。作为一个内部关系错综复杂的经济系统,股票市场与复杂网络系统之间存在许多相似的特征。通过构建复杂网络,不仅可以从整体网络的角度把握股票市场联系的紧密程度,也可以通过对网络拓扑性质的分析,更清晰地了解股票市场内部的相关关系。因此,本文采用复杂网络方法,通过构建股票指标关联网络来把握股票间的联动关系。
具体方法是运用股票交易数据,比如股票价格、成交量以及其他相关指标,计算指标之间的关联关系。在网络中,每只股票作为一个节点,两支股票间的关联关系作为它们之间的边,边的权重则表示具体关联关系的大小,这样就得到了一个复杂网络。通过分析具体网络的性质,就可以对股票之间的关联关系有更明确的了解。根据研究需要,本文构建的为加权无向图,应用权邻接矩阵来表示股票之间的关联关系。该类型的复杂网络不考虑方向,仅考虑节点之间相关关系大小。
2. 股票关联网络构建步骤
本文以股票价格波动关联网络的构建为例,参考张来军等[21]的做法。主要包括以下几个步骤:一是选取固定的时间范围,通过计算得到股票价格波动的相关系数矩阵;二是根据第一步的结果,计算股票之间的距离矩阵;最后是根据求得的距离矩阵,运用合适的方法,例如阈值法、最小生成树等方法,进行复杂网络的构建。
首先计算股票价格波动,也就是股票收益率,本文选用日收盘价数据进行计算,时间范围为[t0, t0+T]。选取任意股票i,在t日,股票i的价格为Pi(t),计算收益率的时间周期为Δt,则t日股票的对数收益率ri(t)表示为:
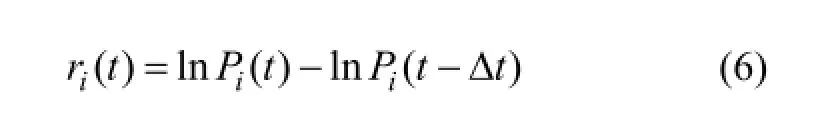
其中,Pi(t)为t日股票的收盘价格,Δt为1日。
根据(6)式,得到N支股票的收益率序列,可以由此计算股票价格收益率间的相关系数。股票i和j之间的相关系数ρij表示为:
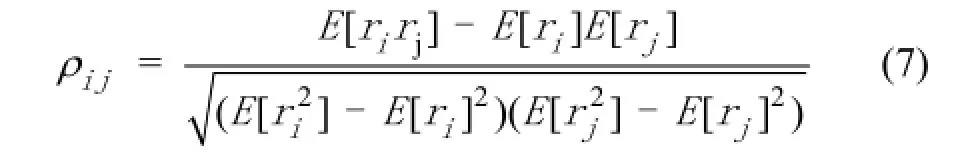
其中:ri和rj分别是股票i和j的价格收益率序列。
将装有试样的石墨坩锅装入感应炉内,抽真空至650 Pa,再通氩气至常压以保证炉内为无氧环境.通电,将炉温升至2000 ℃左右(红外测温),并在此温度下保温3 h.加热期间每隔20 min抽真空至650 Pa,然后通氩气至常压以保证炉内为无氧环境.加热完毕后,待炉温在氩气保护下降至室温,取出石墨件即得到有涂层的石墨片.
由式(7)得到股票间的相关系数,可以得到股票价格波动的相关系数矩阵C。C矩阵中第i行j列的元素记为cij,当i=j时,cij=1;当i≠j时,cij=ρij。可知矩阵C为对称矩阵,且由于ρij∈[-1,1],因此矩阵C中的元素cij∈[-1,1]。
得到相关系数矩阵之后,就需要定义股票之间的度量距离,将相关系数矩阵C转化为距离矩阵D。D矩阵中第i行j列的元素记为dij,有:

由此得到距离矩阵D。根据式(8)可以发现,股票之间的相关系数越大,它们之间的度量距离则相对越小。此时,距离矩阵D为全连接矩阵,为了剔除部分冗余的边,突出重点,需要采取一定的方法进行筛选。经常采用的方法包括阈值法、MST方法等。
本文选用阈值法进行筛选,根据股票间相关系数的分布选取恰当的阈值,再通过阈值对相关系数进行筛选。将相关系数绝对值视为边的权重,通过与阈值的比对,剔除小于阈值的边。通过这种方法,就将一部分冗余的边从网络中剔除了,余下有价值的边,形成了最后的股票关联网络,更便于对网络的拓扑性质进行分析。
五、实证分析
(一) 样本数据
本文的研究样本为我国沪深300指数的成分股,沪深300指数成分股占据了沪深股票市场中60%左右的市值,因此具有较好的代表性;研究期间为 2011 年1月4日至2015年12月31日。为了确保样本数据的准确性,进行如下处理:①剔除成分股中数据缺失的样本;②剔除成分股中金融类股票样本;③剔除成分股中年均交易日低于140天的样本。处理之后剩余共224只股票。本文所使用的股票日度数据,包括股票价格、成交量以及市盈率等,均来自wind数据库。
(二) 股票系统性风险贡献分析
本文运用分位数回归的方法分别计算出了分位数q为0.05、0.01时,个股的CoVaR和ΔCoVaR。用来表示各成分股对整体系统性风险的溢出和贡献度,使用的软件为Stata11.0。个股数量较多,本文给出了个股在q为0.05、0.01时ΔCoVaR的分布情况(图1)。同时,列出q=0.05时,系统性风险贡献度排名前20的成分股情况(表1)。由于计算得到的CoVaR和ΔCoVaR为负值,为便于理解和观测,在此均取绝对值。
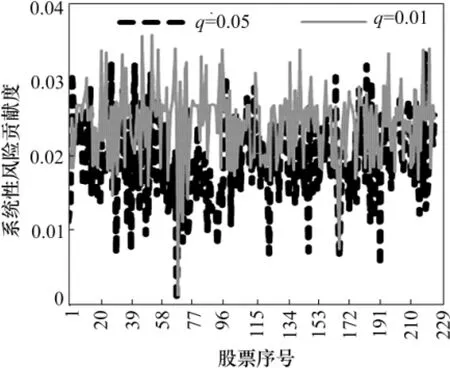
图1 各成分股ΔCoVaR结果
从图1来看,在分位数q分别为0.05和 0.01时,成分股系统性风险贡献度ΔCoVaR的测算结果呈现出一致趋势。各只成分股的ΔCoVaR值差异较大,在0 到0.04的范围内波动,说明不同的成分股对整体的系统性风险贡献存在较大区别,大部分股票的 ΔCoVaR值在0.02上下波动,而有个别股票的ΔCoVaR值接近甚至低于0.005,说明当其处于风险状态时,对整个股票市场的系统性风险影响也不大。表1列出了q为0.05时,成分股中系统性风险贡献度排名前20的股票,这些股票一旦陷入风险状态,可能对整个股票市场形成较大影响,导致较大的系统性风险。
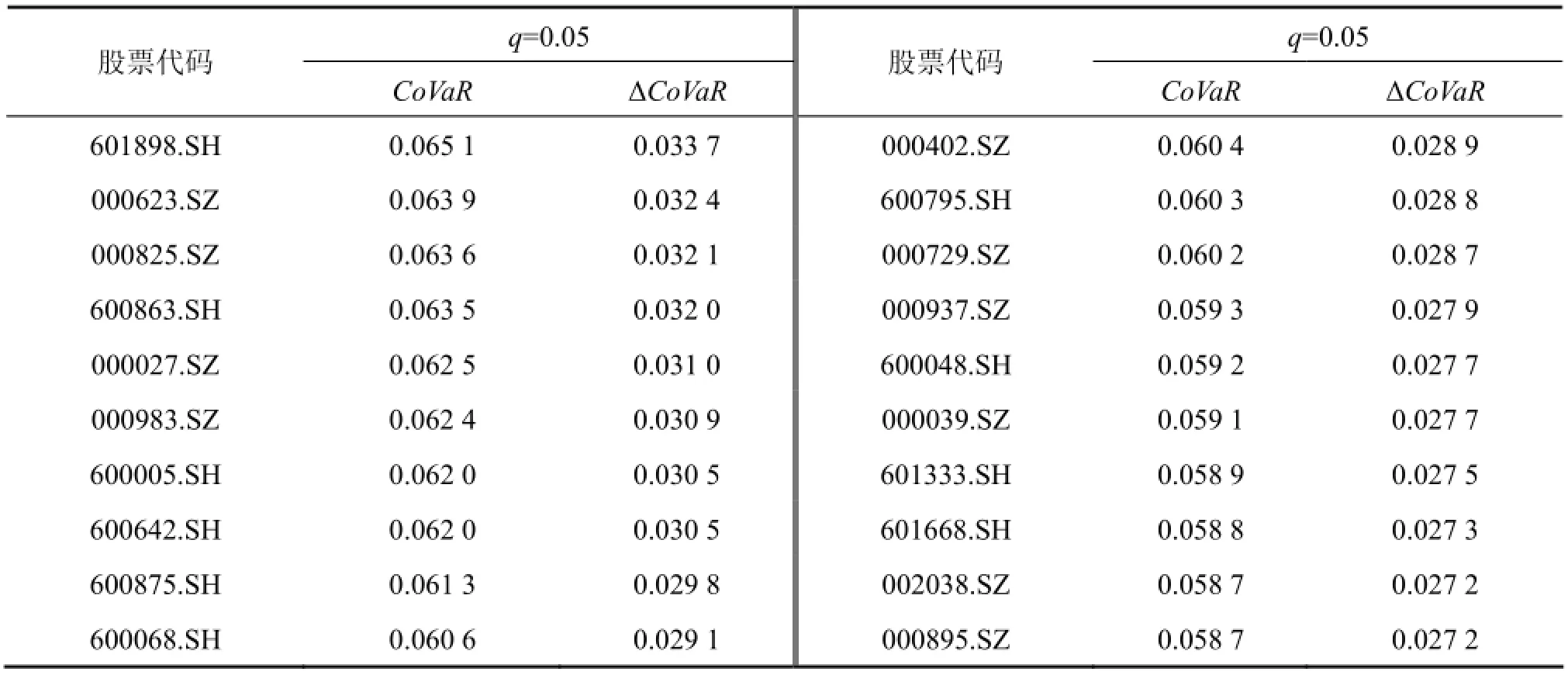
表1 系统性风险贡献度测算结果(前20名)
(三) 股票关联网络分析
根据上述方法,构建股票价格关联网络。在复杂网络的构建中,阈值的设定十分重要,会影响网络中连结边的数量以及聚类系数等网络拓扑结构。相关系数阈值设定过大会导致网络中节点过少难以准确反映股票系统的关联状态,但阈值设定过小又会导致研究对象过多,不具有代表性。本文参考张来军等的做 法[21],根据绝对相关系数值的分布选择阈值。运用Matlab R2014a软件画出沪深300指数成分股股票价格、成交量以及市盈率的绝对相关系数分布图,发现股价相关系数大部分分布在0.4以上,成交量相关系数大部分分布在0.5以上,市盈率相关系数大部分分布在0.4以上,因此在构建沪深300指数成分股股票价格、成交量以及市盈率关联网络,选择的阈值分别为0.4、0.5和0.4。Lee等认为当阈值处于0.4到0.6之间时,股票相关性复杂网络具有无标度性,因此本文的阈值选择是较为合理的[22]。
通过Ucinet和Pajek软件,画出关联网络结构拓扑图,见图2至图4,得到关联网络的统计特征,见表2。
从以上股票指标关联网络的拓扑结构图和统计特征表中可以看出,各只成分股的指标之间存在错综复杂的相关关系。股票价格网络、成交量网络以及市盈率网络的平均路径长度,与同节点数的随机网络相比 都偏小。股票价格网络、成交量网络和市盈率网络的聚类系数分别为73.7%、78.4%和69.7%,都远高于同节点数的随机网络,说明股票指标内部关联性较强。相对而言,市盈率网络中的联动关系最弱。
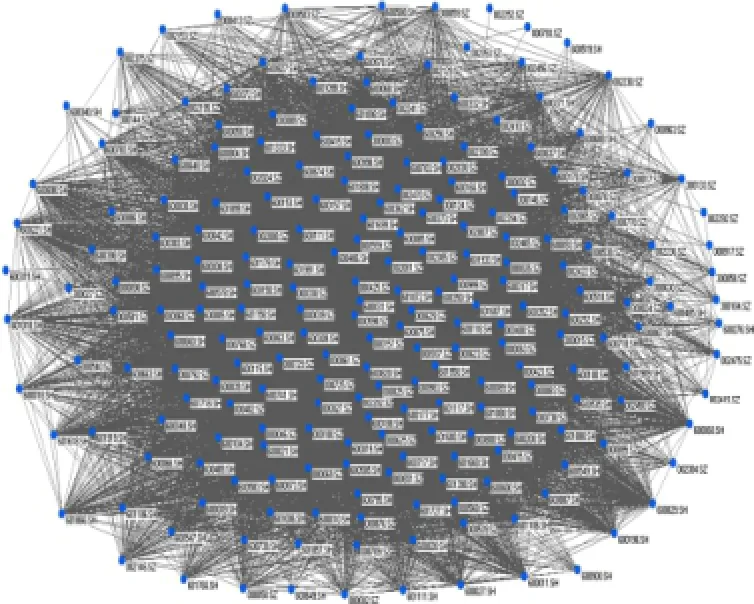
图2 股价关联网络拓扑图

图3 成交量关联网络拓扑图
为得到各只成分股的关联度,需要运用网络节点重要性指标,这是寻找网络中关键节点的常用方法。网络中节点重要性指标主要包括度中心性、介数中心性、接近中心性以及特征向量中心性等。根据这些指标各自的特点,本文最后采用度中心性指标来表示股票指标网络中节点之间的关联程度,得到各成分股在关联网络的重要性。度中心性一般定义为该节点的度
与该网络中最大可能的度值之比,一个节点的度越大就意味着这个节点越重要。图5给出了股价、成交量、市盈率网络中度中心性指标的分布情况,表3列出了股价关联网络中排名前60的成分股及其度中心性。
根据图5可以看出,在本文构建的股价、成交量以及市盈率关联网络中,节点的度中心性分布较为均匀,大量节点的度中心性处于较高的水平,说明关联网络中节点间的联动关系复杂,关联性较强。
(四) 相关性分析

图4 市盈率关联网络拓扑图
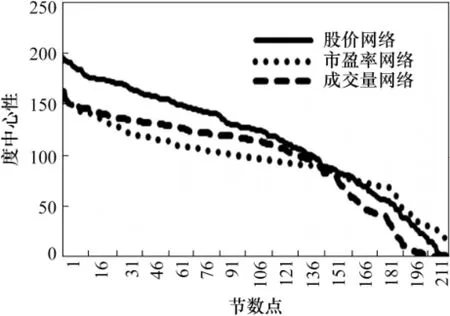
图5 股票关联网络度中心性
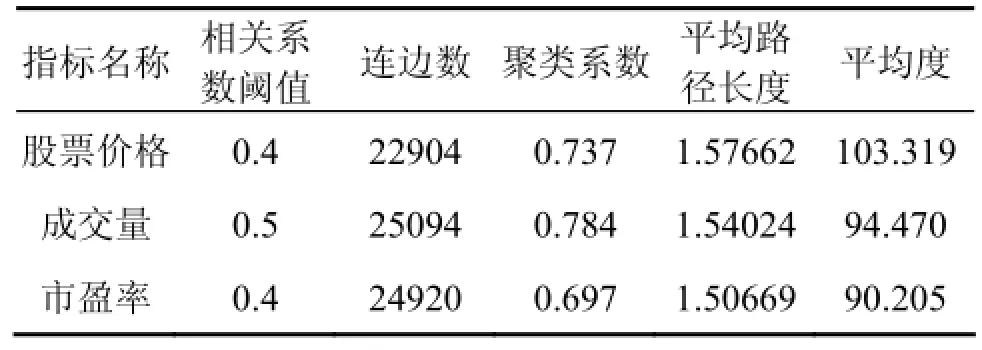
表2 股票各指标关联网络统计特征
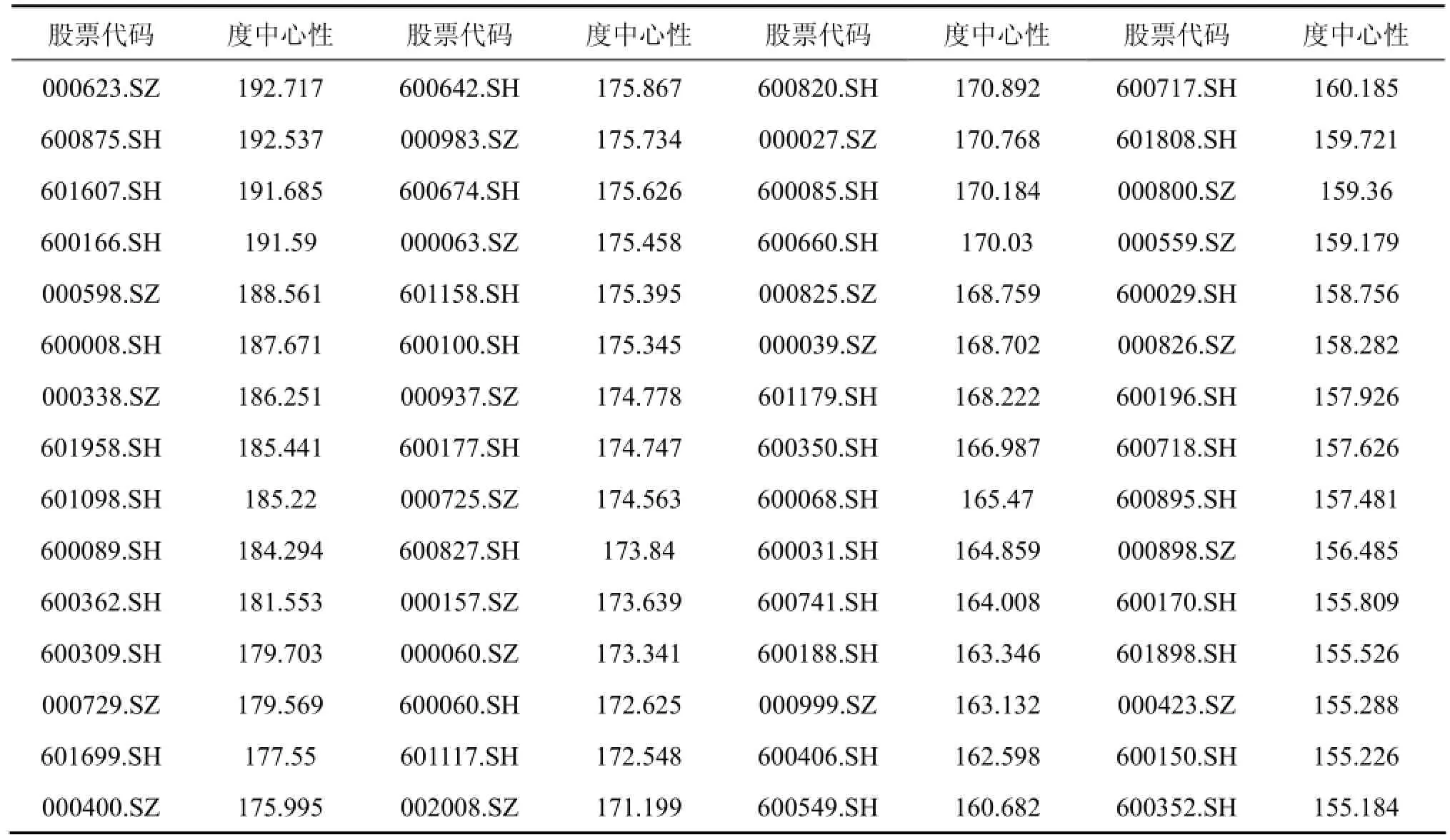
表3 股价关联网络度中心性测算结果(前60名)
根据上文的测算结果,可以对股价指标、成交量指标以及市盈率指标的关联度与系统性风险贡献度之 间的相关性进行分析。
首先,直观地从表1和表3 的测算结果来看,系统性风险贡献度测算结果排名前10的成分股,有8只在股价关联网络度中心性排名中位于前60的范围内,且另外两只股票股价关联网络度中心性排名分别为63位和67位,在股价关联网络中仍处于靠前的位置。可以发现,对整体系统性风险贡献度较高的成分股,一般而言在整个股价关联网络中处在较为重要的位置。
接下来,为验证股票指标关联度与系统性风险贡献度的关系,本文运用Stata11.0软件计算股票关联度指标与ΔCoVaR绝对值之间的相关系数,所得结果如表4。
根据表4的相关性分析结果,股票指标关联性与系统性风险之间,确实存在一定的正相关关系,且不同股票指标与系统性风险间的关系有所不同,与本文研究假设是一致的。
其中,股价关联网络中,成分股度中心性与其系统性风险贡献度之间,存在较强的相关关系,相关系数为66.85%。说明在股价关联网络中与其他节点之间关联性越强的成分股,对股票市场整体的系统性风险贡献较高,当其处于风险状态时,可能对市场整体造成较大影响;成交量关联网络中,成分股度中心性与其系统性风险贡献度之间也存在显著且稳定的正相关关系,相关系数达到44.30%,成交量关联网络中处于核心位置的股票,对市场整体的系统性风险贡献度也越高;市盈率关联网络中,成分股度中心性与系统性风险贡献度(q=0.05)之间存在显著的正相关关系,但与系统性风险贡献度(q=0.01)之间不存在显著的相关关系,说明市盈率指标关联性与其系统性风险贡献度的正相关关系并不稳定。
(五) 回归分析
为进一步分析股票价格以及成交量的关联关系对 成分股系统性风险贡献度的影响,通过选取与股票系统性风险贡献值有关的控制变量,以股票关联网络中心度作为解释变量,个股系统性风险贡献度作为被解释变量进行回归分析。本文以股价关联关系为例进行具体分析,首先构建如下模型:
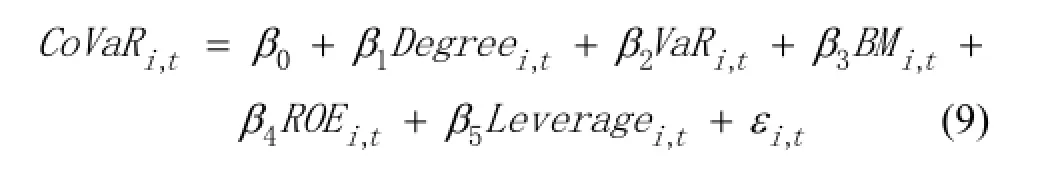
其中:CoVaR为各成分股历年系统性风险贡献测度值,Degree为历年沪深300指数价格关联网络中的度中心性值,表示股价关联性。控制变量的选择,是在考虑系统性风险贡献度影响因素的基础上,参考郭卫东[23]的做法,主要包括:上市公司自身风险(VaR)、公司成长性(BM)、公司资产收益率(ROE)和公司杠杆比(Leverage),并对年度变量(Year)进行控制。本文在运用混合回归模型、固定效应模型以及随机效应模型进行估计后发现,样本具有个体效应,故拒绝混合回归模型。且Hausman检验结果显示,P值为0.00,因此采用固定效应模型进行参数估计,得到结果如表5。
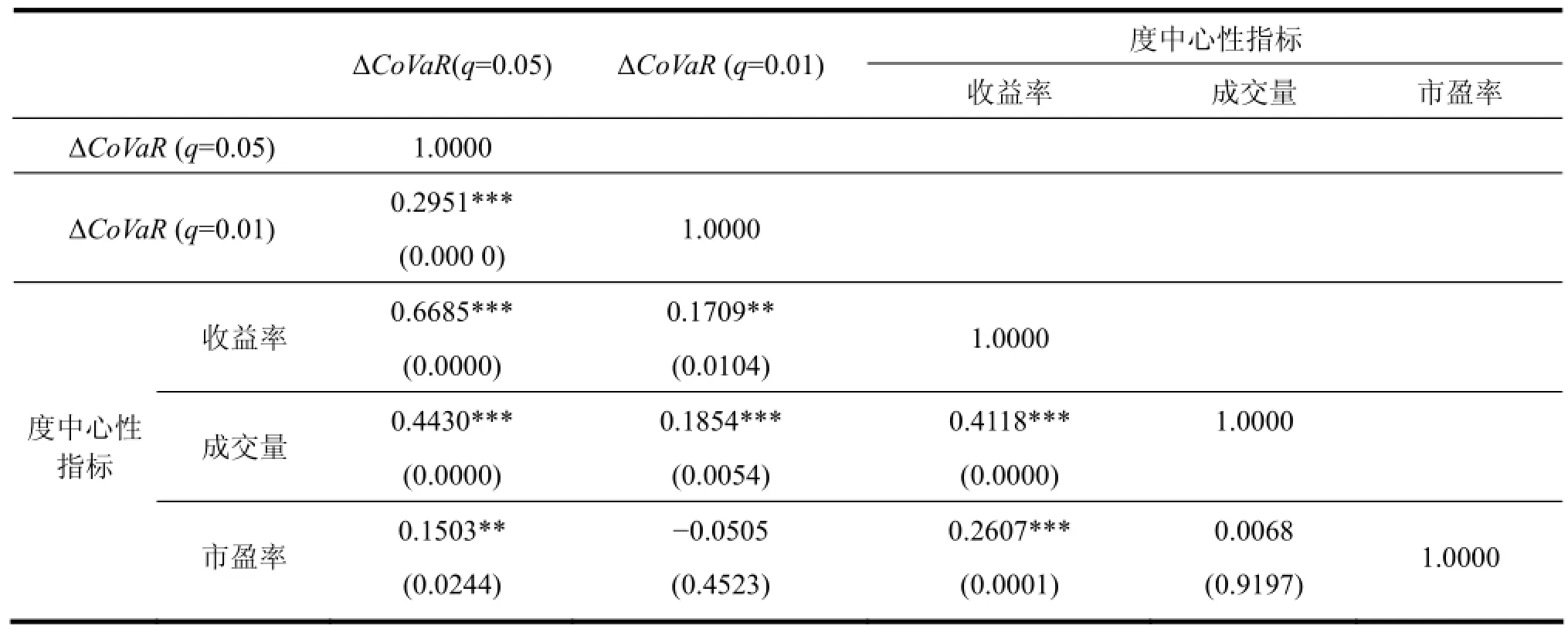
表4 相关性分析结果
根据表5,回归模型调整后的R2值为0.8682,说明模型拟合较好。其中,Degree的系数在0.01的置信水平下显著为正,说明成分股的股价关联性越强,其对市场的系统性风险贡献值会越高,这与本文的理论假设一致。其余控制变量的结果如下:VaR的系数显著为正,上市公司自身的风险越高,其对市场的系统性风险贡献越大;BM系数显著为负,说明成长性越高的公司,对市场整体的系统性风险贡献值越低。ROE
的系数显著为正,说明公司盈利能力越强越大,当其处于风险状态时,市场整体的系统性风险越大;而公司的负债水平与其系统性风险贡献度之间,未呈现出显著的相关关系。
同时,为了对模型的稳健性进行检验,本文对解释变量股票关联度指标进行了替换。参照采用陈忠阳和刘志洋[14]的做法,运用股票间的绝对相关系数均值(Corr)来表示股票之间的关联关系,采用相同的方式重新进行估计,结果如表6所示。可以发现,主要变量的系数方向与显著性水平基本保持不变,验证了模型的稳健性。
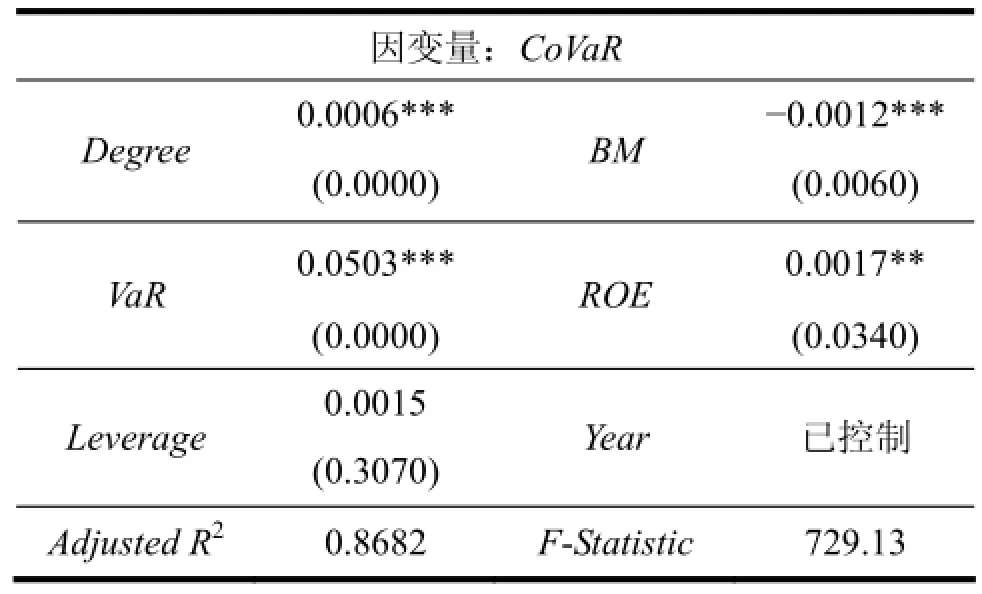
表5 回归分析结果
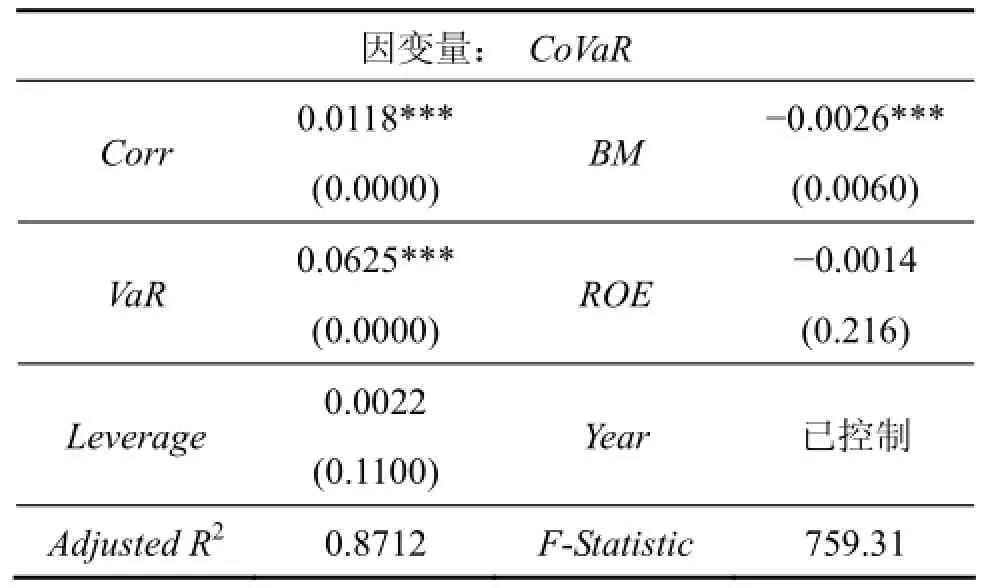
表6 稳健性检验结果
按同样的方法对股票成交量的关联关系对系统性风险贡献度的影响进行回归分析,以成交量关联网络中度中心性的值作为解释变量,个股系统性风险贡献度作为被解释变量,采用固定效应模型进行参数估计,得到相似的结果:模型调整后的R2值为0.8204,且在0.01的置信水平下解释变量系数显著为正,说明成分股的成交量关联性越强,其系统性风险贡献度越高。
研究结果说明,股票之间的关联性与其对市场整体的系统性风险贡献之间存在正相关关系,股票之间错综复杂的联系可能导致系统性风险的产生与传递,在股票指标关联网络中处于核心地位、与其他节点关联性越强的股票,对股票市场的系统性风险贡献度更高。根据股票指标关联网络的节点重要性指标,可以找到这些关联度广、关联性强的成分股,这类型成分股一般规模较大,在行业中具有较强的影响力,与其他股票之间联动性强,可以对整个股票市场产生影响,导致较大的系统性风险,因此需要给予更高的关注。
六、结论与建议
本文基于沪深300指数成分股股票关联网络,对成分股的系统性风险贡献进行研究。从理论上说明了股票关联性与系统性风险之间的联系,并验证了两者之间的相关关系,得出以下结论:①股票之间错综复杂的关联关系是系统性风险的产生与传递的基础; ②在股票指标关联网络中,关联度越广、关联性越强的股票,对市场整体的系统性风险贡献度越高;③不同股票指标关联度对系统性风险的预警作用不同,股票价格指标关联性对系统性风险的预警作用最强,而市盈率指标关联性与系统性风险之间的关系不稳定,不能有效预警系统性风险。
基于以上结论,本文从关联度的角度出发,为系统性风险管理提出如下建议:第一,股票之间的过度联动可能导致风险的传递与扩散,形成较大的系统性风险。因此需要通过制度建设和投资者引导等手段缓解我国股市过度联动现状。一方面,加快证券市场制度建设,逐步推进市场化进程,同时加强对信息披露的监管,提高市场透明度,降低股价同步性;另一方面,引导投资者形成理性投资观,同时积极培育机构投资者,降低市场投机性。第二,根据股票指标之间的关联关系把握股票市场内部联动性,可以将其作为系统性风险的预警指标,通过了解股票间的关联程度,为系统性风险的防控提供参考。第三,对市场中规模较大、影响力较强、关联度较广的上市公司给予更高的关注,一旦这类型公司陷入风险状态,可能引发整个市场的剧烈波动。因此,需要注意这类公司的经营状况和股市行情,把握其异常状态,及时防范和控制系统性风险。
[1] Mishky F. Comment on systemic risk [J]. Research in Financial Services: Banking, Financial Markets, and Systemic Risk, 1995(7): 31-45.
[2] Kaufman G, Scott E K. What is systemic risk, and do bank regulators retard or contribute to it? [J]. Independent Review, 2003, 7(3): 371-391.
[3] Bemanke, B. Financial reform to address systemic risk [R]. Washington D C: Council on Foreign Relations, 2009.
[4] Sharpe W F. A Theory of market equilibrium under condition of risk [J]. Journal of Finance, 1964, 19(3): 111-127.
[5] Baumol, William. An expected gain-confidence limit criterion for portfolio selection [J]. Management Science. 1963(11): 174-182.
[6] Adrian T, Brunnermeier M K. CoVaR [R]. National Bureau of Economic Research, 2008.
[7] 柏满迎, 吴琪, 吴天都. 我国股票市场与基金市场间的风险溢出研究[J]. 统计研究, 2014(4): 108-109.
[8] 费兆奇. 国际股市一体化与传染的时变研究[J]. 世界经济, 2014(9): 173-192.
[9] 梁琪, 李政, 郝项超. 中国股票市场国际化研究:基于信息溢出的视角[J]. 经济研究, 2015(4):150-164.
[10] Battiston S, Gatti D D, M Gallegati. Default cascades: When does risk diversification increase stability? [J]. Journal of Financial Stability, 2012, 8(3): 138-149.
[11] Markose S, Giansante S, Shaghaghi A. ‘Too interconnected to fail’ financial network of US CDS market: Topological fragility and systemic risk [J]. Journal of Economic Behavior & Organization, 2012(3): 627-646.
[12] Gai, Prasanna, Andrew Haldana, and Sujit Kapadia. Complexity, concentration and contagion [J]. Journal of Monetary Economic, 2011, 58(5): 453-470.
[13] 范小云, 方意, 王道平. 我国银行系统性风险的动态特征及系统重要性银行甄别——基于CCA与DAG相结合的分析[J]. 金融研究, 2013(11): 82-95.
[14] 陈忠阳, 刘志洋. 国有大型商业银行系统性风险贡献度真的高吗——来自中国上市商业银行股票收益率的证据[J]. 财贸经济, 2013(9): 57-66.
[15] 隋聪, 迟国泰, 王宗尧. 网络结构与银行系统性风险[J]. 管理科学学报, 2014(4): 57-70.
[16] Jin L, Myers S C. R2around the world: New theory and new tests [J]. Journal of Financial Economics, 2006, 79(2): 257-292.
[17] Longin F. Solnik B. Is the correlation in international equity returns constant: 1960—1990? [J]. Journal of International Money and Finance, 1995, 14(1): 3-26.
[18] Ang A, Chen J. Asymmetric correlations of equity portfolios [J]. Journal of Financial Economics, 2002(3): 443-494.
[19] Pollet J, Wilson M. Average correlation and stock market returns [J]. Journal of Financial Economics, 2010(3): 364-380.
[20] 郑振龙, 王为宁, 刘杨树. 平均相关系数与系统性风险: 来自中国市场的证据[J]. 经济学(季刊), 2014(3): 1047-1064.
[21] 张来军, 杨治辉, 路飞飞. 基于复杂网络理论的股票指标关联性实证分析[J]. 中国管理科学, 2014(12): 85-92.
[22] Lee K E, Lee J W, Hong B H. Complex networks in a stock market [J]. Computer Physics Communications, 2007, 177(1): 186.
[23] 郭卫东. 中国上市银行的系统性风险贡献测度及其影响因 素——基于 MES方法的实证分析[J]. 金融论坛, 2013(2): 16-21.
[编辑: 谭晓萍]
Analysis of systemic risk contribution of CSI 300 Index: Based on the stock correlation network
QIAO Haishu, YANG Lei
(School of Finance and Statistics, Hunan University, Changsha 410082, China)
Using individual stocks as nodes to build the network based on the CSI 300 Index, and then using CoVaR method to measure the contribution of stocks to systemic risk, the present study aims at the relationship between the size of correlation of individual stocks in the stock market and its systematic risk. Findings show that the nearer a stock is to the core of the stock correlation network, the higher systematic risk contribution. This illustrates that in the stock market, the stocks with wider correlation are more likely to transfer risks, and contribute more to systemic risks. So, in supervising and preventing systematic risks, we must pay more attention to those companies with wider correlation in the market and stronger influence.
systemic risk; stock correlation; complex network; CoVaR method
F830.9
A
1672-3104(2016)03-0114-10
2016-03-20;
2016-05-26
乔海曙(1971-),男,安徽桐城人,经济学博士,湖南大学金融与统计学院教授,博士生导师,主要研究方向:金融分析与管理;杨蕾(1993-),女,湖南汨罗人,湖南大学金融与统计学院硕士研究生,主要研究方向:金融分析与管理

