赫姆霍兹声腔声学特性实验研究

许晓勇，刘红珍（北京航天动力研究所，北京100076）



赫姆霍兹声腔声学特性实验研究

许晓勇，刘红珍
（北京航天动力研究所，北京100076）

摘要：为了研究赫姆霍兹谐振器声腔结构参数变化对声学特性的影响，采用传递函数法在驻波管实验系统上进行了谐振器的冷态声学特性实验。实验结果表明：影响谐振频率的最大因素是声腔开口直径，其次是进口孔壁厚，其他因素如声腔长高比等影响较小；开口直径对谐振带宽影响最大且呈近似线性关系，其他参数则存在最优值能使得带宽最大、有效阻尼的频率范围最宽；多进口复合谐振声腔的谐振频率变化不大，而带宽增加显著。为确保有效抑制不稳定燃烧，赫姆霍兹谐振器声腔在设计和制造时应重点控制进口孔的相关状态参数。

关键词：赫姆霍兹谐振器；声腔；声学特性；传递函数法

0　引言

在液体火箭发动机中，当燃烧室内燃烧过程压力脉动的频率与燃烧室的某一声振频率耦合时会出现高频不稳定燃烧，对燃烧室产生极大的破坏。声腔通过与燃烧室声振频率主动耦合，改变燃烧室的声振特性，耗散声波的传播能量，从而有效地阻尼不稳定燃烧，提高推力室的动态稳定性。

赫姆霍兹谐振器声腔与四分之一波长管声腔相比，在保证调谐体积的情况下，结构尺寸可调节范围较宽，占用空间小，进入腔体的高温燃气较少，结构适应性较好，是一种典型的吸声频带较窄的声学吸收器，即在谐振频率附近阻尼效果很好，偏离一定频率则效果减弱。因此，开展赫姆霍兹谐振器声腔结构参数变化对谐振频率、频带宽度等声学特性影响的实验研究对声腔设计具有积极的意义。

赫姆霍兹谐振器理论最早于1860年由赫姆霍兹提出，此后这种谐振器广泛地用作声滤波器和噪声抑制器。20世纪50年代至70年代，美国详细研究了赫姆霍兹谐振器的工作特性，先后成功用来抑制航空喷气发动机中的燃烧振荡和用于液体火箭发动机的阻尼装置［1］。20世纪80年代，欧洲研制的Vulcain氢氧火箭发动机采用赫姆霍兹谐振器来提高推力室对高频不稳定燃烧的阻尼能力［2］。本世纪初，西门子公司研制的SGT6系列燃气轮机使用赫姆霍兹谐振器有效抑制了高频和中频不稳定燃烧［3］。国防科技大学的聂万胜等人通过声学分析比较了用于抑制液体火箭发动机不稳定燃烧的赫姆霍兹声腔和四分之一波长管声腔的阻尼特性，提出根据声吸收系数优化系统阻尼［4］。中国科学院声学所的刘克和清华大学的唐旭东等人通过理论分析和驻波管声学实验研究了赫姆霍兹谐振器系统的声场特性［5］，给出了流动对谐振器性能的影响［6］，同时还数值模拟和测量了谐振器喉部的非线性效应［7］。

本文利用驻波管采用传递函数法对不同结构尺寸和孔状态的赫姆霍兹谐振器声腔的声学特性进行了研究，得到了声腔结构参数变化对谐振频率和谐振带宽等声学特性的影响规律。

1　赫姆霍兹谐振器原理

赫姆霍兹谐振器如图1所示，其由经小孔与燃烧室相连的小容腔组成［8］。在谐振器的特征尺寸远小于所调谐的振荡波长的情况下，谐振器内气体的运动特性类似于质量-弹簧-阻尼系统。可得谐振频率为

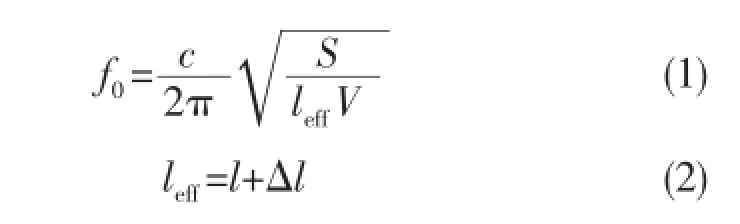
式中：c为谐振腔内的平均声速，由腔内介质的温度及成分确定，对于空气S为谐振腔进口孔的截面积，S=0.25πd2，d为开口直径；V为谐振腔体积；leff为谐振腔进口孔的有效长度；l为进口孔的实际物理长度；Δl为考虑到在孔端附近的流动效应而进行的长度修正。

对于孔的末端修正量Δl的修正，选取了2种方法，一种是在噪声水平较低时［8］：

另一种是对于不存在明显气流通过的孔［9］：

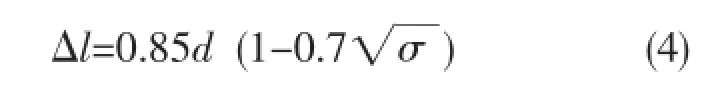
式中σ为谐振腔进口孔的开口面积比即孔截面积与腔截面积的比值。

图1　赫姆霍兹谐振器声腔原理图Fig.1　Principle diagram of Helmholtz cavity

2　声学实验系统

实验采用双传声器测量传递函数的方法，进行环境空气条件下的冷态声学实验，从而获得谐振频率、吸收系数以及声阻抗等参数。实验装置及测试系统主要包括信号控制仪、功率放大器、扬声器、传声器、赫姆霍兹谐振器试件、驻波管及信号分析仪等。信号控制仪可以产生随机或正弦信号，经过功率放大器后输入到扬声器产生带宽白噪声输出，带宽频率范围可以根据研究范围设定。传声器采集的声压信号输入到信号分析仪进行相关分析。实验系统如图2所示。

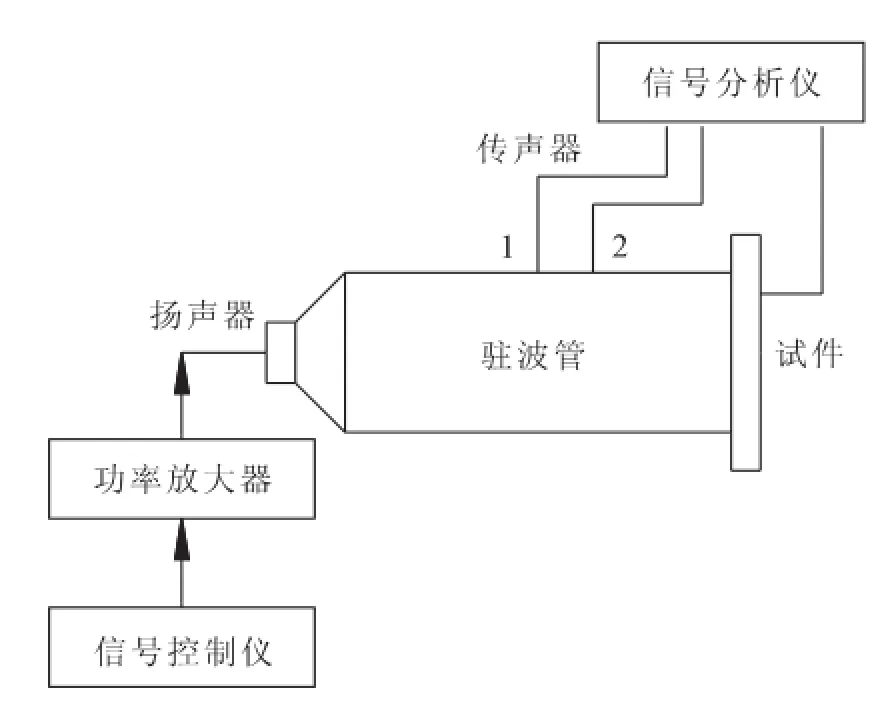
图2　双传声器传递函数法实验系统示意图Fig.2　Experiment system of double-microphone transfer function method

2.1传递函数法测量声阻抗原理［10］

将传声器A和B按图2中的位置1和2分别装好，测定传递函数交换2个传声器，即传声器A测量2处，传声器B测量1处，测量传递函数

测定2个位置间的复传递函数：

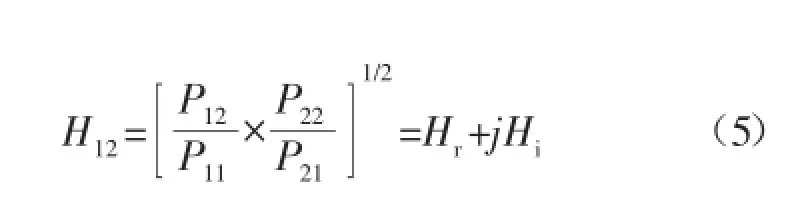
式中：Hr为H12的实部；Hi为H12的虚部。

确定反射因子：

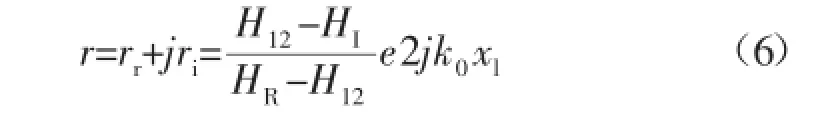
式中：rr为反射因子的实部；ri为反射因子的虚部；xl为试件到远的传感器的距离；入射波的传递函数HI=e-jk0s；反射波的传递函数HR=e-jk0s；波数k0=2πf/c0；S是两个传声器间的距离。

吸声系数α的测定：

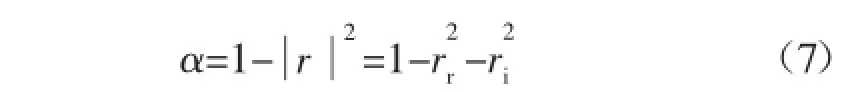
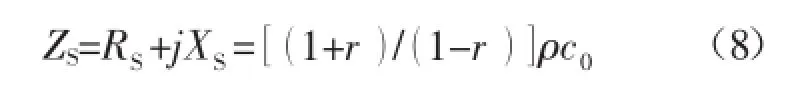
式中：RS为声阻，声阻抗的实部；XS为声抗，声阻抗的虚部；ρc0为空气的特性阻抗。

2.2实验装置

2.2.1驻波管

驻波管又称阻抗管，是一种用来测量吸声材料或结构的垂直入射吸声系数的装置［11］。本实验根据试件形状采用50 mm×50 mm方形截面的驻波管，材料为不锈钢。传声器安装孔有2个，沿管壁布置，间距60 mm，靠近试件的传声器安装孔距离试件表面35 mm。驻波管全长650 mm，工作频率范围为400～2 000 Hz。驻波管如图3所示。

声阻抗：

图3　驻波管实验装置Fig.3　Experiment device of standing wave tube

2.2.2声腔试件

为研究赫姆霍兹谐振器声腔的开口直径、进口孔壁厚、进口孔边缘状态、长高比和进口孔个数对谐振频率和谐振带宽的影响，设计了不同尺寸的声腔试件。试件材质为不锈钢，由声腔腔体和底板2部分焊接而成，在声腔的底部声压最大处布有测孔，底板上布置了6个螺栓孔，用以与驻波管对接。声腔模型剖视图如图4所示。

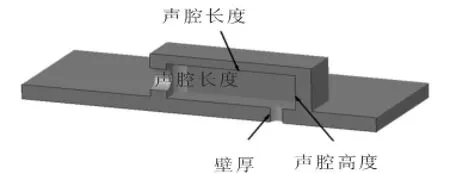
图4　声腔试件剖视图Fig.4　Cutaway view of cavity sample

3　实验结果及分析

根据传递函数法原理，利用Matlab软件编程对实验数据进行了处理，得到吸声系数和声阻抗等参数。某声腔试件吸声系数如图5，吸声系数最大值对应频率为1 014 Hz，即谐振器的谐振频率，吸声系数最大值的0.707倍所确定的谐振频率宽度为谐振带宽。根据声腔试件的声阻、声抗及声阻抗3条幅值曲线的交点也可以确定谐振频率，与吸声系数确定的谐振频率相比，最大偏差小于1%，因此本文仅采用吸声系数来确定声腔试件的实验谐振频率。

该声腔试件采用SYSNOISE软件数值模拟计算了声腔内的压力分布，声腔底部压力最大值对应的频率即谐振频率模拟值为1 010 Hz。根据声腔的理论计算公式（1）采用末端修正公式（3）计算得到理论谐振频率（以下简称理论值1）为975 Hz，采用末端修正公式（4） 得到的频率（以下简称理论值2）为100 9 Hz。对其他声腔试件的测量和计算数据进行了同样处理。

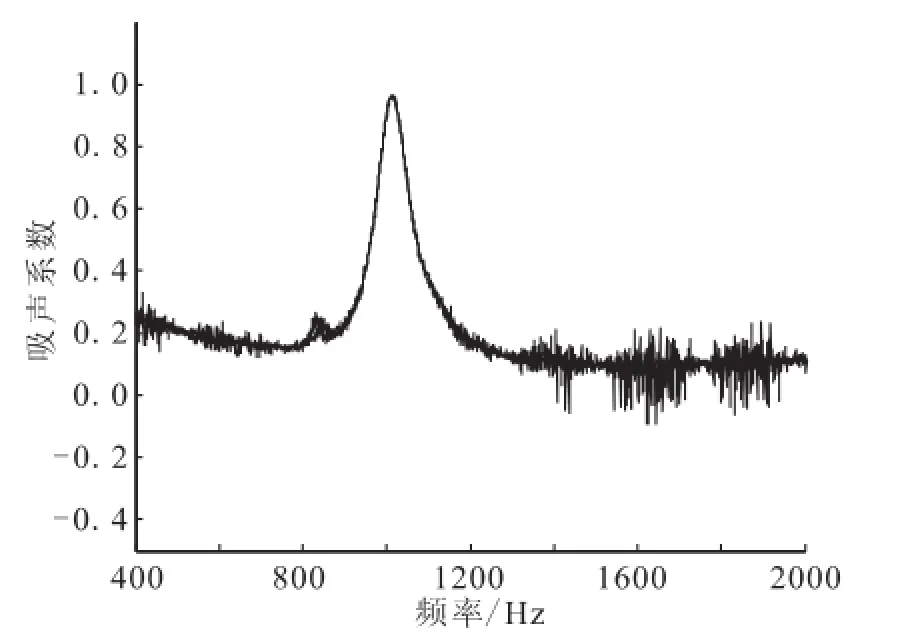
图5　某声腔试件吸声系数Fig.5　Acoustic absorption coefficient of a cavity sample

3.1声腔进口孔相关状态对声学特性的影响

3.1.1声腔开口直径

在声腔长度、宽度、高度及进口壁厚不变的情况下，对开口直径分别为2 mm，4 mm，9.2 mm，10.1 mm及12 mm的声腔试件进行了计算、模拟和实验。图6为声腔谐振频率随开口直径变化的关系曲线，声腔的谐振频率随开口直径的增加而近似线性的增加，变化显著。对于理论计算，当开口直径与进口孔壁厚大于1时，修正公式（4）的结果偏离大，而修正公式（3）的结果精确度好，因此对于不同的结构参数应该选用不同的孔末端修正公式。

如表1所示，谐振带宽随着开口直径的增大也呈近似线性增大的规律，增加幅度明显，当开口直径从2 mm增大到12 mm时，谐振带宽从50 Hz增加到162 Hz，增大了3倍多。谐振带宽越大，则覆盖的谐振频率越宽，从而使得声腔在偏离设计谐振频率的情况下仍具有较高的吸声系数［1］，能够增强设计状态与热试状态谐振频率偏差的容错能力以及燃烧室工况变化造成声学频率变化的适应能力。但是，开口直径大则热燃气更易于进入声腔内部，不利于结构热防护。

图6　声腔谐振频率随开口直径变化关系Fig.6　Variation of resonant frequency of acoustic cavity with inlet diameter

3.1.2声腔进口孔壁厚

在声腔长度、宽度、高度以及进口孔直径不变的情况下，分别对孔壁厚即进口孔长度为1.5 mm，3 mm，4 mm，6 mm及8 mm的5种声腔试件进行了计算、模拟及实验。图7为声腔谐振频率随壁厚变化的关系曲线，声腔的谐振频率随声腔进口孔壁厚的增加而迅速减小，壁厚每增加一倍，谐振频率降低约15%。与开口直径的结果不同，调整孔壁厚，理论值2比理论值1更接近实验值、更精确，末端修正公式（4）更准确。

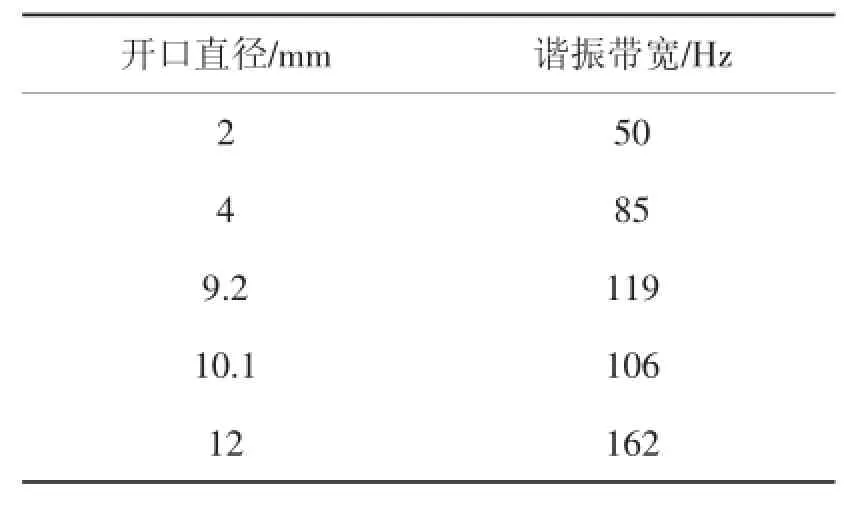
表1　不同开口直径声腔的谐振带宽Tab.1　Resonant bandwidth of cavity with different inlet diameter

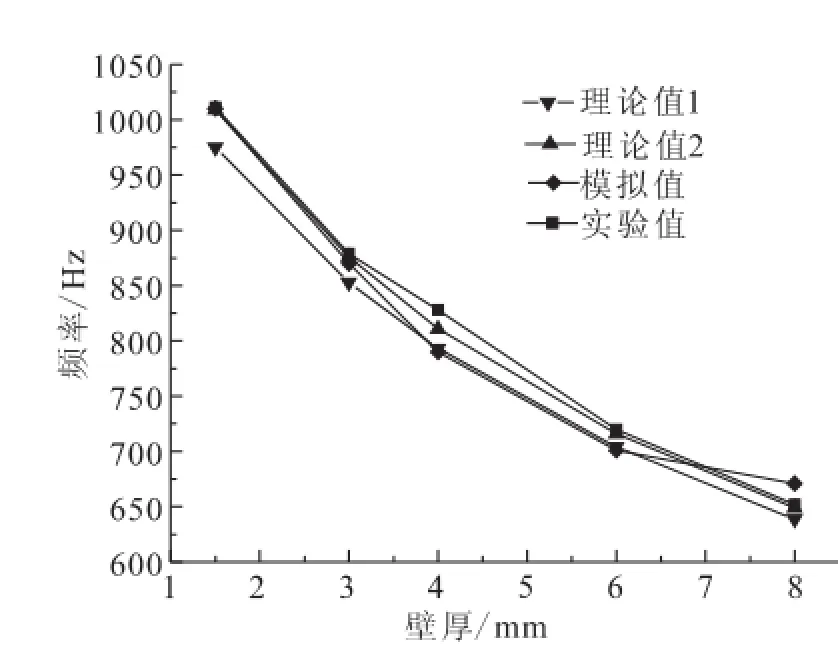
图7　声腔谐振频率随壁厚变化关系Fig.7　Variation of resonant frequency of acoustic cavity with wall thickness

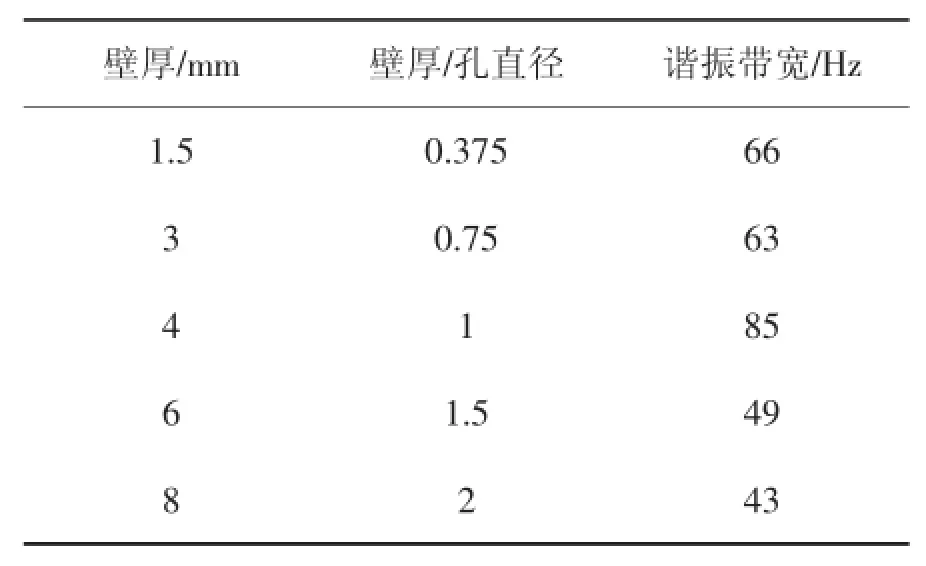
表2　不同进口孔壁厚声腔的谐振带宽Tab.2　Resonant bandwidth of cavity with different wall thickness

表2为通过实验获得的不同进口孔壁厚声腔试件的谐振带宽。谐振带宽随进口孔壁厚与孔直径之比的增加先增大然后再减小，当壁厚与孔直径相等时谐振带宽最大，同时薄壁孔比厚壁孔的带宽普遍要大，因此为获得良好的有效阻尼频率范围，在结构强度允许时壁厚应薄一些，这与NASA的C.B.McGough等人的研究结果基本一致［12］。

3.1.3声腔进口孔边缘状态

在声腔其他结构参数不变的情况下，仅变化声腔的进口孔的边缘状态，如图8所示，分为孔上端倒R=1圆角、孔上端倒R=2圆角、孔上端倒1×45°倒角和孔上下两端各倒R=1圆角共4种状态，研究了声腔进口孔边缘状态对声学特性的影响。

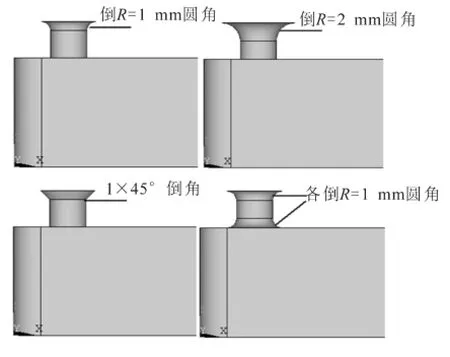
图8　不同边缘状态进口孔声腔模型Fig.8　Cavity model of different edge state

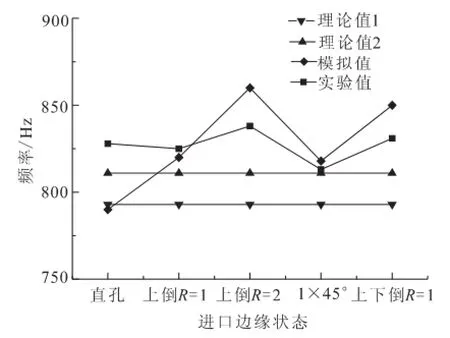
如图9所示，实验结果表明，不同进口孔状态的谐振频率有较小的差别：直角进口与较小的倒圆进口频率基本相当；进口孔上边缘倒圆角的半径越大，谐振频率越大；对孔2边倒圆角比对孔一边倒圆角的谐振频率大；进口倒1×45°倒角的谐振频率最小。上述不同进口孔状态谐振频率的变化与进口附近的局部声阻变化规律一致。可见，声腔进口孔边缘越光滑，曲率越小，则进口附近的局部声阻会降低，而声腔谐振频率会略微增大。模拟值也反映出同样规律且变化幅度更大，而理论公式无法计算孔边缘状态的区别。

对于谐振带宽，实验结果见表3，局部声阻较大（进口倒1×45°倒角）或较小（孔上端倒R= 2圆角或孔上下两端各倒R=1圆角）时谐振带宽均比声阻适中（直孔或孔上端倒R=1圆角）时要小，直孔的带宽最大。

3.2声腔长高比对声学特性的影响

保持声腔宽度、进口壁厚、进口孔直径以及总容积不变，改变声腔的长度和高度，对5种长高比的声腔试件进行了计算、模拟及实验。图10为谐振频率随声腔长高比变化的曲线，谐振频率随声腔长高比的增加而减小。谐振带宽则是先增大然后再减小，存在一个带宽最大、性能最优的长高比，见表4。当长高比小于等于最优长高比时，谐振频率变化很小，而谐振带宽则在长高比从最小变化到最优时增加约50%，明显的提高了声腔有效阻尼的频率范围，增强了阻尼能力。随着长高比的继续增大，声腔沿推力室轴线的长度增加、沿半径方向的尺寸减小，声腔趋于变长变薄，谐振频率和带宽都迅速降低，阻尼能力降低。

3.3复合谐振声腔对声学特性的影响

保持单个声腔的结构参数不变，组合成单腔双孔和单腔三孔复合谐振声腔，如图11所示。声腔的宽度与进口个数成正比，即保持声腔的开口面积比不变。

实验结果表明，声腔谐振频率随进口个数的增加而略微减小，最大变化不超过2.2%，带宽则3个进口比1个和2个进口显著增加，增幅约28%，见图12和表5。进口增加产生的谐振频率最大偏移为18 Hz，远小于增加后的谐振带宽109 Hz，也小于带宽的增加值24 Hz，因此增加声腔的进口个数也即采用复合谐振声腔是有益的，可以增加有效阻尼的频率范围，增强声腔的适应能力。数值模拟结果与实验结果规律一致。

在推力室中，过多的进口会带来声腔结构强度以及腔内声波横向振荡的问题。具体到某一个推力室，作为基本声腔单元的复合谐振声腔，其进口个数需要根据声腔在推力室中的工作环境、连接结构和抑制的不稳定振型具体分析和权衡优化，可以采用数值模拟的方法进行预估。

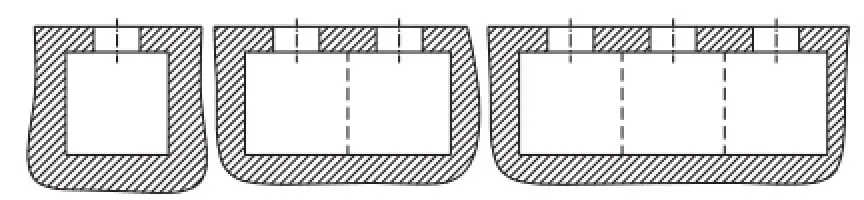
图11　复合谐振声腔形状Fig.11　Shape of composite resonator

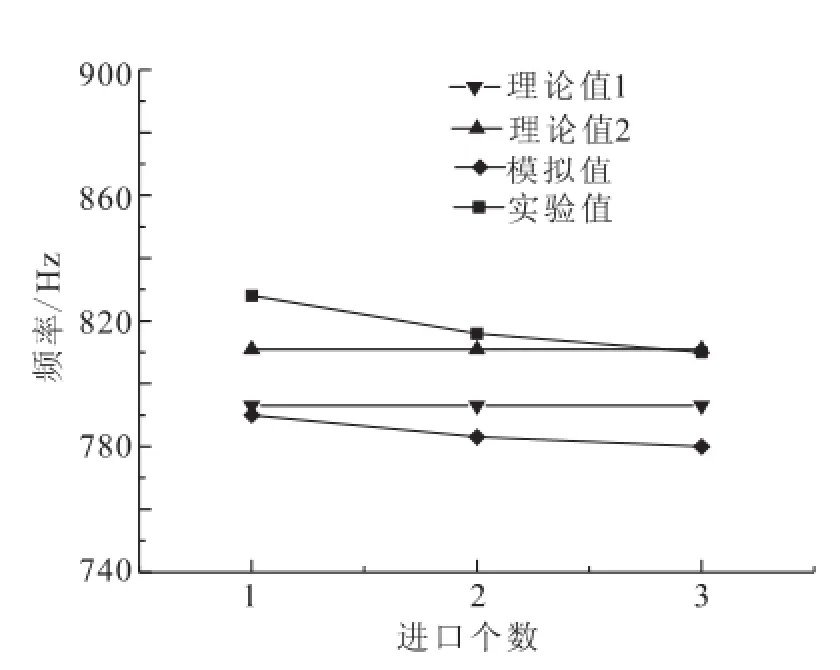
图12　声腔谐振频率随进口个数变化关系Fig.12　Variation of resonant frequency with inlet quantity

表5　不同进口个数声腔的谐振带宽Tab.5　Resonant bandwidth of cavity with different inlet quantity

3.4不同参数对声腔声学特性影响的比较

对于声腔的谐振频率，实验结果表明最大影响因素是声腔开口直径，其次是进口孔壁厚，这两个因素都是进口孔的相关状态，而声腔的结构形状如长高比的影响较小。因此，在谐振器设计和制造时应重点关注和控制进口孔的相关状态参数，确保其谐振频率与需要抑制的燃烧室声振频率相吻合。

对于谐振带宽，最大影响因素同样是声腔开口直径，其他参数的影响则各不相同，且对一些参数存在最优值，从而能确保声腔的谐振带宽最大，有效阻尼的频率范围最宽，声腔的适应能力更强。因此在确保结构协调、强度和传热安全可靠的情况下谐振器的相关结构参数应尽量取在最优值附近，以最大化谐振带宽。

4　结论

本文利用驻波管采用传递函数法对不同结构尺寸和孔状态的赫姆霍兹谐振器声腔的声学特性进行了研究，得到了声腔结构参数变化对谐振频率和谐振带宽等声学特性的影响规律。得到的主要结论如下：

1）对于声腔进口孔的相关状态，随着开口直径的增加，谐振频率和谐振带宽近似线性增加，而进口孔壁厚的增加会导致谐振频率减小且壁厚与孔直径相等时谐振带宽最大，孔边缘状态的影响较小。

2） 谐振频率随声腔长高比的增加而减小，谐振带宽则是先增大然后再减小，存在一个带宽最大、性能最优的长高比；多进口复合谐振声腔的谐振频率变化不大，而带宽增加显著。

3） 影响谐振频率的最大因素是声腔开口直径，其次是进口孔壁厚，长高比等因素的影响较小；开口直径对谐振带宽影响最大且呈近似线性关系，其他参数则存在最优值能使得带宽最大、有效阻尼的频率范围最宽。

4） 用理论公式计算谐振频率时，为获得较为精确地计算结果，应根据声腔结构选用合适的孔末端修正公式；对于进出口倒圆等不规则腔体的声腔，数值模拟具有优势。

参考文献：

［1］哈杰D T，里尔登F H.液体推进剂火箭发动机不稳定燃烧 ［M］.朱宁昌，张宝炯译.北京：国防工业出版社，1980.

［2］KIRNER E，OECHSLEIN W.Development status of the Vulcain（HM60）thrust chamber：AIAA 90-2255［R］.USA：AIAA，1990.

［3］LIEUWEN T C，YANG Vigor.Combustion instabilities in gas turbine engines［M］.USA：AIAA，2005.

［4］聂万胜，庄逢辰.声腔应用于液体火箭发动机不稳定燃烧抑制中的特性研究［J］.国防科技大学学报，1998，20 （2）：12-16.

［5］刘克，焦风雷，唐旭东.具有Helmholtz共振器的驻波管系统声场的研究［C］//中国声学学会.2002年全国声学学术会议论文集.上海：声学技术编辑部，2002，65-66.

［6］焦风雷，刘克，郭庆.具有流动和侧向Helmholtz共振器的驻波管内声场实验研究［C］//中国声学学会.2003年青年学术会议论文集.上海：声学技术编辑部，2003，44-46.

［7］刘克，蒋剑，彭锋.强非线性条件下Helmholtz共振器喉部声学特性研究［J］.声学技术，2004，23：3-4.

［8］杨V，安德松W E.液体火箭发动机燃烧不稳定［M］.张宝炯译.北京：科学出版社，2001.

［9］PBILLIPS B，HANNUM N P，RUSSELL L M.On the design of acoustic liners for rocket engine：Helmholtz resonators evaluated with a rocket combustor：NASA TN D-5171［R］.USA：NASA，1969.

［10］李晓东.声学阻抗管中吸声系数和声阻抗的测量第2部分：传递函数法：GB/T 18696.2-2002［S］.中华人民共和国国家标准（国家质量监督检验检疫总局发布），2002.

［11］张琪.L形声学谐振器的吸声特性试验［J］.强度与环境，2011，38（5）：31-35.

［12］MCGOUGH C B.Acoustic liner feasibility program：NASA CR 111405［R］.USA：NASA，1970.

（编辑：马杰）

中图分类号：V433-34

文献标识码：A

文章编号：1672-9374（2016）03-0068-08

收稿日期：2015-11-23；修回日期：2016-02-09

作者简介：许晓勇（1979—），男，高级工程师，研究领域为液体火箭发动机推力室

Experiment study on acoustic characteristics of Helmholtz cavity

XU Xiaoyong，LIU Hongzhen
（Beijing Aerospace Propulsion Institute，Beijing 100076，China）

Abstract:In order to study the influence of structure change of Helmholtz acoustic cavity on acoustic characteristics，the transfer function method was used to carried out some experiments of cold state acoustic characteristic on the standing wave tube experimental system.The test results indicate that the first factor affecting the resonant frequency of the cavity is the inlet diameter，the second one is the wall thickness of inlet，and the other factors such as length to height ratio of the cavity have less influence；the inlet diameter has the greatest influence on the resonant bandwidth and has an approximate linear relationship，and the influence of other parameters exists the optimal value which can make the bandwidth maximum and the frequency range of effective damping widest；the resonant frequency of multi-inlet composite resonator changes little and the bandwidth increases significantly.To effectively suppress the combustion instability，the correlated status parameters of the inlet aperture diameter must be controlled emphatically in design and manufacture of Helmholtz resonator's acoustic cavity.

Keywords:Helmholtz resonator；acoustic cavity；acoustic characteristic；transfer function method