压裂液流速差对井口八通注入头冲蚀磨损影响

邹凤彬，邱亚玲，祖宝华

(1.西南石油大学 机电工程学院，成都 610500；2.中国石油天然气管道局 第一工程分公司，河北 廊坊 065000)①



压裂液流速差对井口八通注入头冲蚀磨损影响

邹凤彬1，邱亚玲1，祖宝华2

(1.西南石油大学 机电工程学院，成都 610500；2.中国石油天然气管道局 第一工程分公司，河北 廊坊 065000)①

摘要：对页岩气井进行“井工厂”拉链式压裂，施工压力高、排量大。井口八通注入头有6根注入管线，在高速压裂液的冲刷作用下，极易发生冲蚀磨损。基于液-固两相流模型和冲蚀理论建立井口八通注入头冲蚀模型，研究了流速差对井口八通注入头冲蚀速率的影响。研究表明：井口八通注入头的最大冲蚀速率主要发生在注入管线与注入头主管线相连的部位；在一定速度差范围内，流速差越大，井口八通注入头的冲蚀速率越大，可以通过注入管线的连通来降低流速差，达到减小井口八通注入头冲蚀速率的目的。研究结果为减少井口八通注入头的冲蚀磨损提供了一定的参考。

关键词：页岩气；拉链式压裂；注入头；冲蚀磨损；数值模拟

“井工厂”拉链式压裂技术可以提高页岩气的开发效率，降低作业成本。2014-03-09，我国首次采用多井同步拉链式压裂技术，成功对四川宜宾地区的4口页岩气井进行压裂施工。该技术是目前世界上较先进的页岩气“工厂化”压裂技术，理论上能使施工效率提高1倍以上[1-5]。在施工过程中，井口注入头在多根注入管线内高速压裂液的冲刷作用下，极易发生冲蚀磨损。由于泵车激振，地面高压管线布局的复杂性，多根管线之间存在流速差，将会增加注入管线在井口注入头部分汇聚时的流场不稳定性，加速注入头的冲蚀磨损。严重的情况下，井口注入头将会发生刺穿和破裂，威胁现场施工人员的安全，增加施工成本和周期。国内外学者在钻井工艺参数对井口注入头冲蚀磨损的影响进行了大量的研究[6-8]，但对于流速差对井口注入头冲蚀磨损的影响研究较少。本文基于液-固两相流模型和冲蚀理论，建立井口注入头冲蚀模型，并利用该模型研究了流速差对井口注入头冲蚀速率的影响，研究结果为减少井口注入头的冲蚀磨损提供了一定的参考。

1几何模型建立及网格划分

选取页岩气开发“井工厂”拉链式压裂施工过程中普遍使用的井口八通注入头进行研究。井口八通注入头极限工作压力为140 MPa，注入头主管线内径130 mm，注入管线内径70 mm，注入头上下两端面距离840 mm，注入管线轴线与注入头主管线轴线夹角为45°。井口八通注入头的几何模型及流道抽取模型如图1所示。

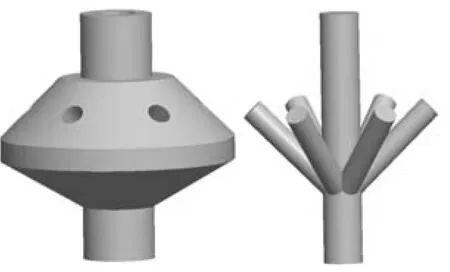
a　几何模型

b　流道抽取几何模型

运用Gambit六面体网格进行井口八通注入头流道抽取模型的网格划分，并在近壁面设置适当的边界层，以保证近壁面数值模拟的准确性。网格划分模型如图2所示。

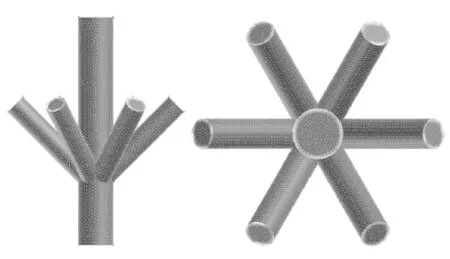
a　整体网格划分

b　端面网格划分

2三维紊流流场数值模型

在井口八通注入头内部，压裂液的流动是复杂的液-固两相流三维紊流问题[9-11]。选用Fluent DPM模型进行八通注入头流场的数值模拟[12]，忽略离散相之间的相互作用，在Eulerian坐标系下求解连续相流体流场，通过Lagrangian坐标系下的离散相固体颗粒作用力微分方程求解固体颗粒运动轨迹方程。湍流模型选用标准模型[13]，运用有限体积法进行求解器的离散。

2.1控制方程

压裂液流体的流动遵循质量守恒定律、动量守恒定律、能量守恒定律等物理守恒定律，根据上述守恒定律并结合牛顿第二定律(以Navie-Stokes方程表示)，可以推得八通注入头内压裂液流体的控制方程[14]。

连续方程

(1)

动量方程

-Δp′+Δ·(μeffΔU)T

(2)

能量方程

Δ·(λΔT)+Δ·(U·τ)+U·SM+SE

(3)

状态方程

p+patm=ρRT

(4)

式中：ρ为密度，kg/m2；t为时间，s；U为流体速度矢量，m/s；μeff为等效黏度，Pa·s；p′为修正压强，Pa；htot为总焓，J/mol；p为静压力，Pa；λ为导热系数，W/(m·k)；T为绝对温度，K；τ为应力，Pa；SM为动量源，W/m3；SE为能量源，W/m3；patm为大气压力，Pa；R为普适气体常数。

2.2湍流模型

标准κ-ε两方程模型为：

(5)

(6)

式中：κ为湍流动能，J；μ为动力黏度，Pa·s；μt为湍流黏度，Pa·s；pκ为剪切湍动能，J；σκ、σε、Cε1、Cε2均为常量；ε为紊流耗散率，m2/s3。

3冲蚀磨损模型

采用颗粒冲蚀与沉积模型[15]，本模型假设固体颗粒以一定角度与壁面撞击后以一反射角弹开[16-17]。该模型定义的冲蚀速率的大小与流体速度、颗粒的冲击角以及颗粒形状函数有关：

(7)

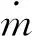
4边界条件及工况参数指定

设定井口八通注入头边界条件为速度入口，压力出口，入口处压裂液和支撑剂颗粒的速度大小、方向相同。壁面移动选择Stationary Wall，剪切无滑移，边界类型reflect，颗粒在壁面反弹引起动量变化，其反弹系数由壁面碰撞恢复系数决定。

数值模拟中，参考某典型页岩气开发施工参数指定：注入管线压裂液流体速度为10.83 m/s，支撑剂颗粒粒径为3×10-4mm，支撑剂颗粒体积分数为10%，支撑剂颗粒视密度2 780 kg/m3，压裂液流体动力黏度为0.01 Pa·s。

5数值模拟结果分析

首先对注入管线中压裂液流体在有流速差与无流速差情况下，井口八通注入头的最大冲蚀速率进行分析，得出注入管线有流速差时井口八通注入头最大冲蚀速率较大的结论，进而提出通过将6根注入管线连通的方案来降低流速差，以降低井口八通注入头的冲蚀速率。

5.1流速差对井口八通注入头冲蚀磨损的影响

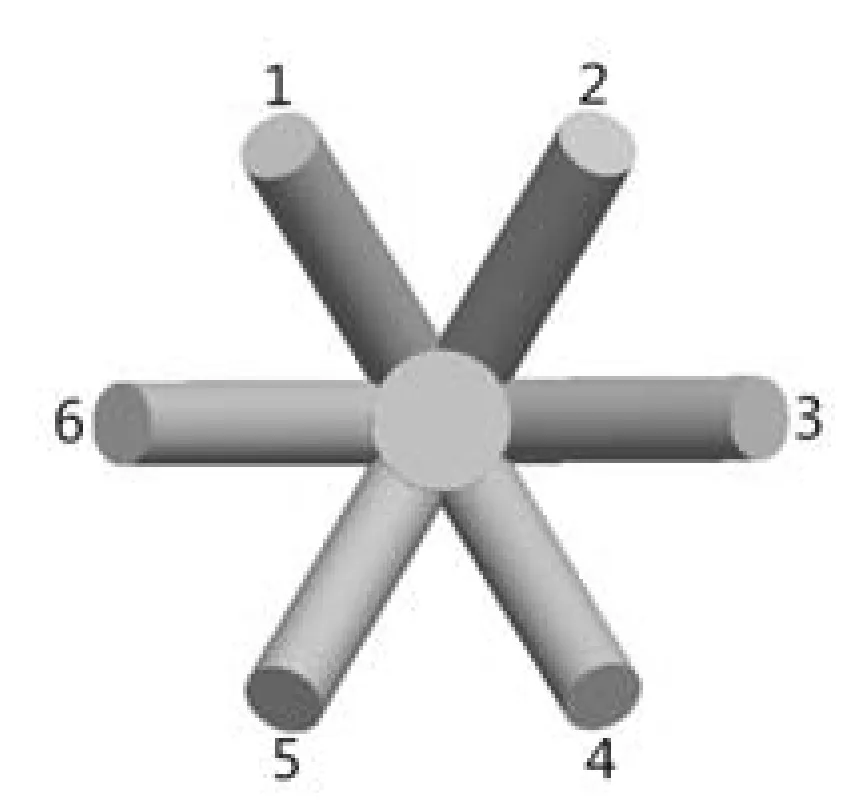
将6根注入管线分为2组，假设其中1、3、5为一速度组，2、4、6为另一速度组，分组如图1所示。当两速度组的流速差为6 m/s时，即当1、3、5速度组的速度为7.83 m/s，2、4、6速度组的速度为13.83 m/s时，计算井口八通注入头的最大冲蚀速率，并计算6根注入管线无流速差，即速度均为10.83 m/s时，井口八通注入头的最大冲蚀速率。计算结果如图3～4所示。

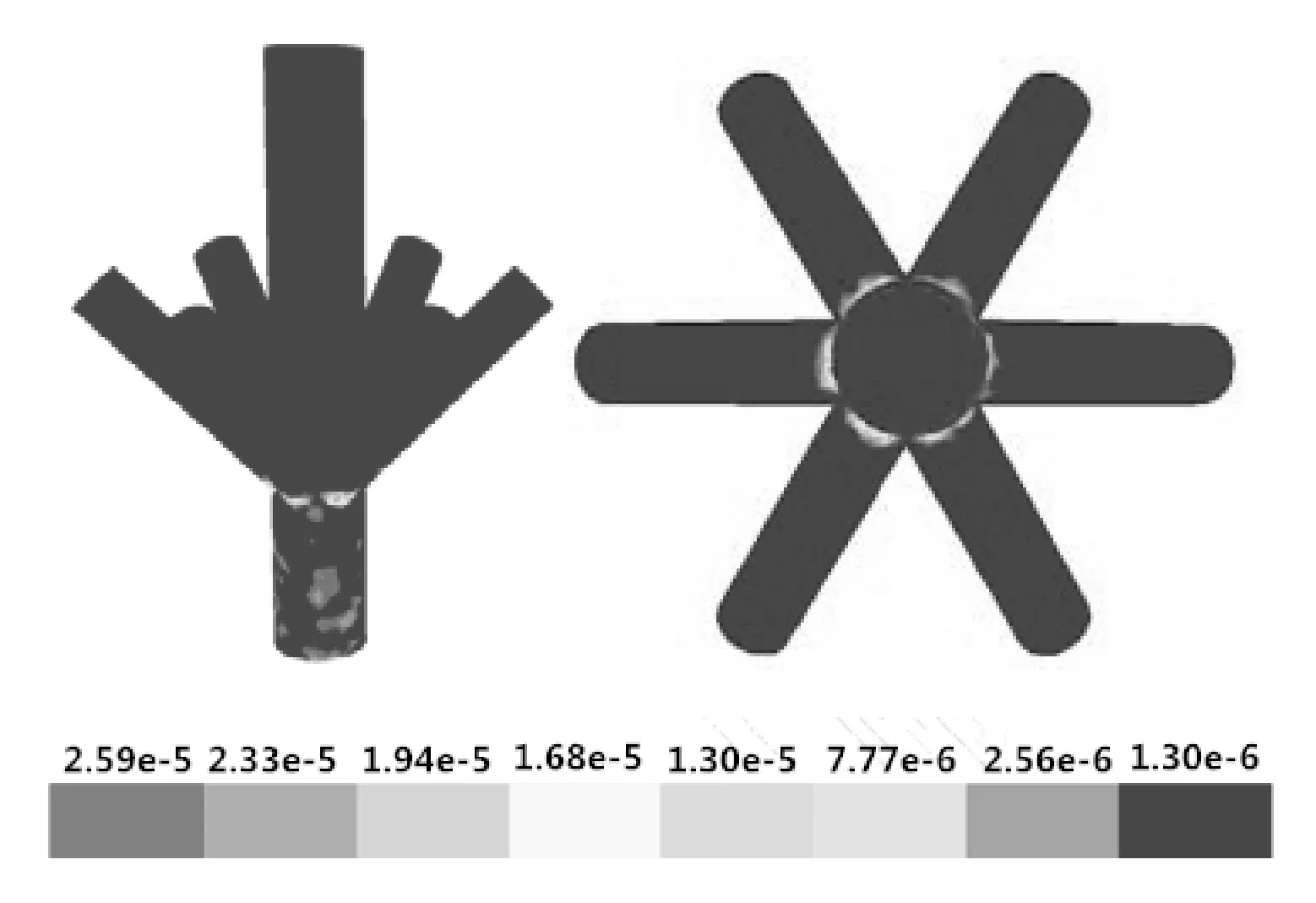
图3　流速差6 m/s时井口八通注入头的冲蚀云图

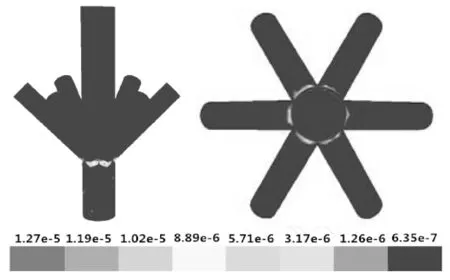
图4　无流速差时井口八通注入头的冲蚀云图

由图3～4可以看出：无论有无流速差，井口八通注入头的最大冲蚀速率均发生在6根注入管线与井口八通注入头主管线连接部位。这是因为6根注入管线中的压裂液在此处流向骤变，6根注入管线中的压裂液在此处发生汇聚，压裂液中支撑剂颗粒速度增大，并且因为6根注入管线中压裂液的汇聚，破坏流场的紊流状态，进一步加剧了压裂液对井口八通注入头的冲蚀磨损。当注入管线中压裂液流体的流速差为6 m/s时，井口八通注入头的最大冲蚀速率为2.59×10-5kg/(m2·s)；当注入管线中压裂液流体无流速差时，井口八通注入头的最大冲蚀速率为1.27×10-5kg/(m2·s)，即井口八通注入头最大冲蚀速率在注入管线流速差为6 m/s时，是注入管线无流速差情况下的2.04倍。虽然6根注入管线的流速差并未影响井口八通注入头最大冲蚀速率的发生位置，但却提高了井口八通注入头的冲蚀速率峰值，使井口八通注入头的冲蚀磨损加重。

5.2管线连通对流速差的影响

在不影响研究结果，将井口八通注入头的6根注入管线连通模型进行简化，即将6根注入管线简化为并排的6根直管线，并在靠近出口端用1根与注入管线等径的直管线进行6根注入管线的连通。同样的将6根管线进行分组，如图5所示。其中1、3、5为一速度组，2、4、6为另一速度组，假设两速度组之间的流速差分别为2、4、6 m/s。与上文研究指定相同的边界条件与工况参数。为确保压裂液流体在管线连通前的流场稳定，取压裂液流体入口至管线连通部位的直管段距离为2 000 mm，运用Gambit六面体网格进行几何模型网格划分，并在近壁面设置适当的边界层，以保证近壁面数值模拟的准确性，网格划分模型如图5所示。

图5　6根注入管线连通简化单元模型

5.2.1流速差为6 m/s时

当1、3、5速度组的速度为7.83 m/s，2、4、6速度组的速度为13.83 m/s，即两组之间的流速差为6 m/s时，通过所建立的数值计算模型，计算得出各出口速度如表1所示。

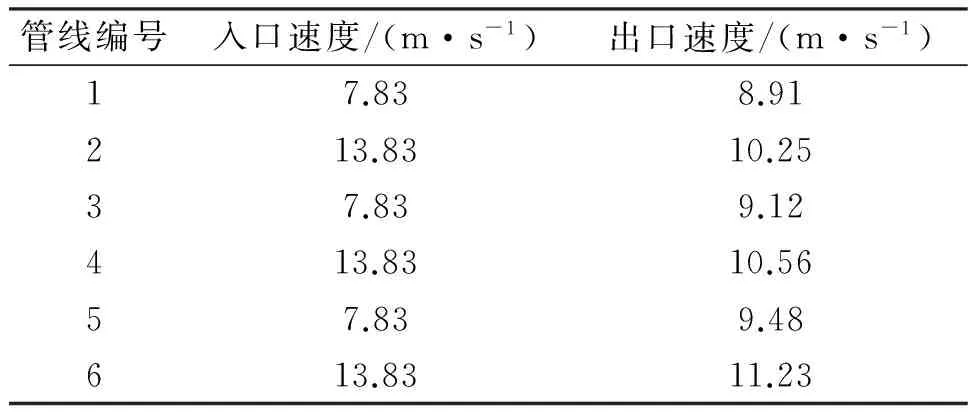
表1　流速差为6 m/s时注入管线连通后出口速度

由表1可以看出，注入管线连通后，各管线之间的流速差降低，连通后各管线之间的最大流速差仅2.32 m/s，较之6 m/s，流速差降低了61.3%。

5.2.2流速差为4 m/s时

当1、3、5速度组的速度为8.83 m/s，2、4、6速度组的速度为12.83 m/s，即两组之间的流速差为4 m/s时，数值计算结果如表2所示：

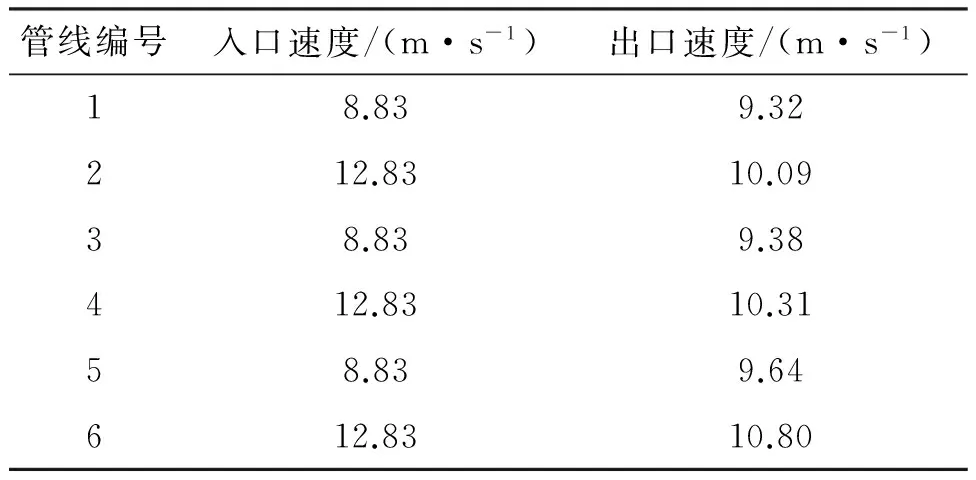
表2　流速差为4 m/s时注入管线连通后出口速度

由表2可以看出，注入管线连通后，各管线之间的流速差降低，连通后各管线之间的最大流速差仅为1.48 m/s，较之4 m/s降幅达到63%。

5.2.3流速差为2 m/s时

当1、3、5速度组的速度为9.83 m/s，2、4、6速度组的速度为11.83 m/s，即两组之间的流速差为2 m/s时，数值计算结果如表3所示：

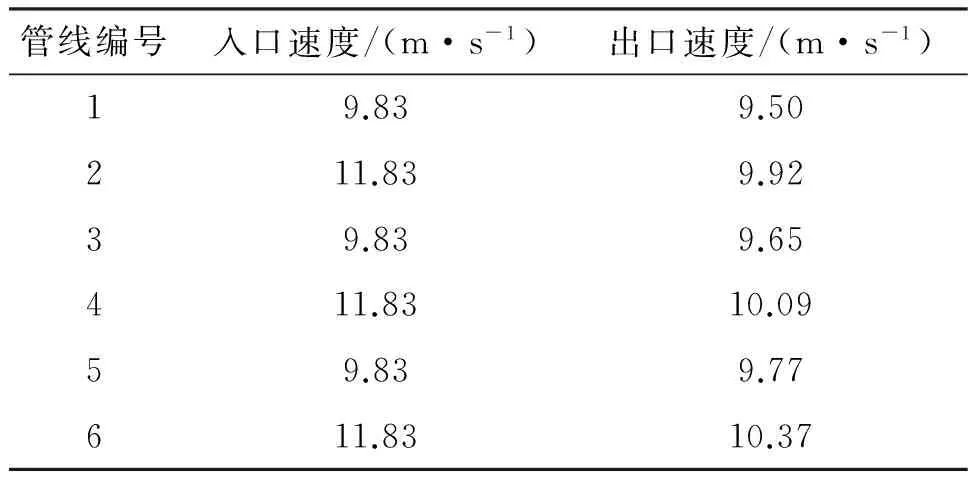
表3　流速差为2 m/s时注入管线连通后出口速度

由表3可以看出，注入管线连通后，各管线之间的流速差降低，连通后各管线之间的最大流速差仅为0.63 m/s，较之2 m/s降低了1.37 m/s，流速差降低幅度达到了68.5%。

分析可知，在一定流速差范围内，6根注入管线的连通可以降低流速差，且当6根注入管线的入口流速差越小时，6根注入管线的连通对流速差的降幅越明显。

6注入管线连通与非连通状态对八通注入头冲蚀磨损的影响

分析注入管线连通对井口八通注入头冲蚀磨损的影响，同样选取图1中1、3、5管线为一速度组，2、4、6为另一速度组，两速度组之间的流速差为2、4、6 m/s，分别研究在上述3种入口流速差的情况下，6根注入管线连通及非连通，八通注入头的冲蚀速率，进一步分析注入管线连通对八通注入头冲蚀磨损的影响。

6.1流速差为6 m/s时

流速差为6 m/s时，管线连通情况下，6根注入管线的入口速度分别输入表1中的出口速度；对比分析组，即管线非连通的情况下，针对注入管线分别输入表1中的入口速度，数值计算结果如图6～7所示。

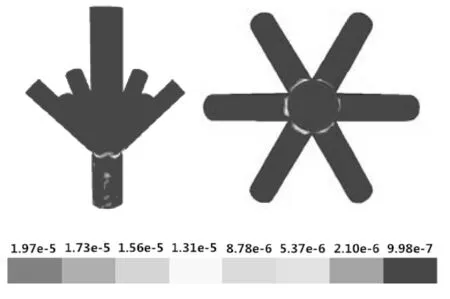
图6　流速差为6 m/s注入管线连通时井口八通注入头的冲蚀云图

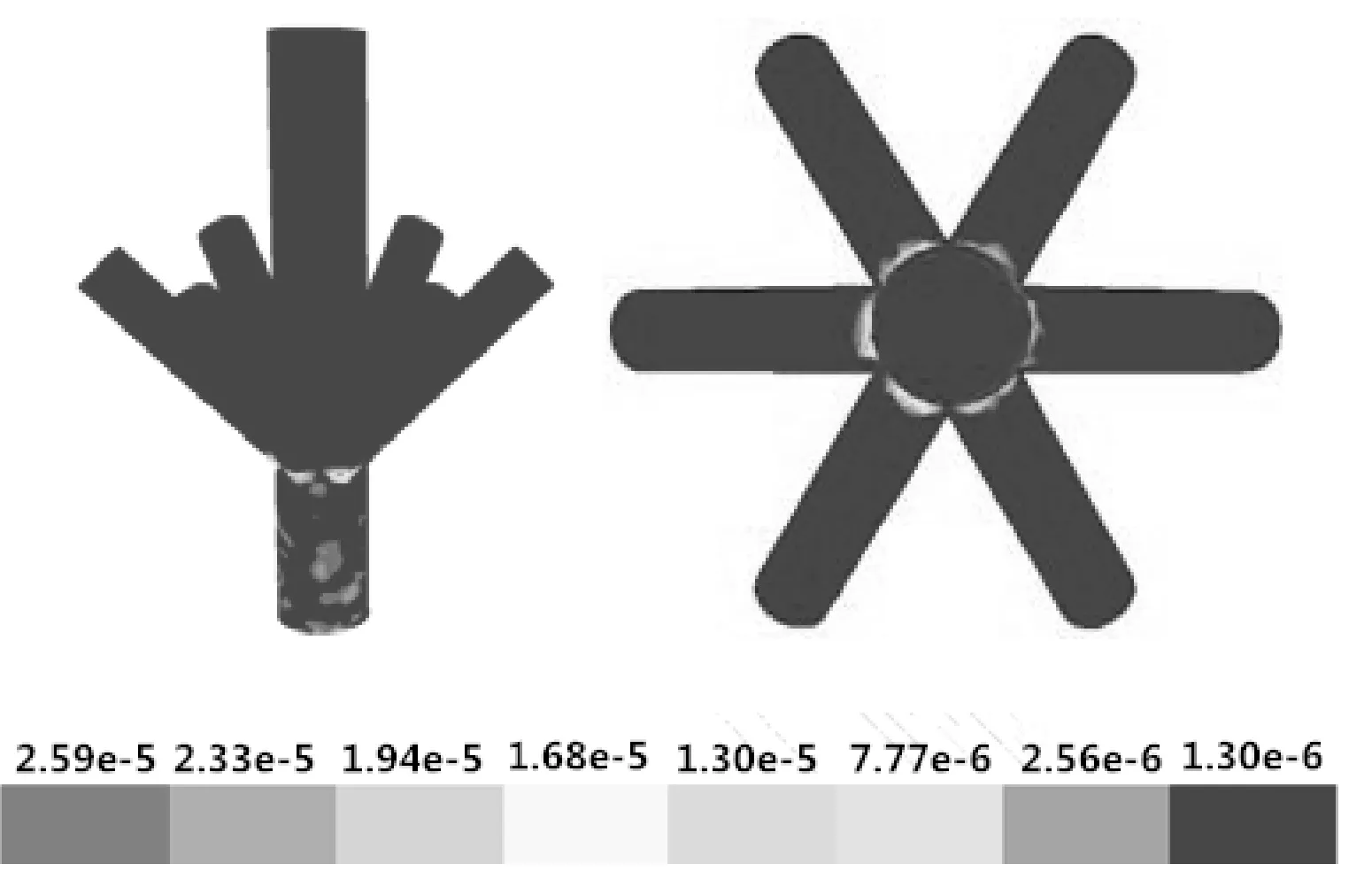
图7　流速差为6 m/s注入管线非连通时井口八通注入头的冲蚀云图

由计算结果可以看出，6根注入管线连通时井口八通注入头最大冲蚀速率为1.97×10-5kg/(m2·s)，6根注入管线非连通时井口八通注入头最大冲蚀速率为2.59×10-5kg/(m2·s)，注入管线连通时井口八通注入头最大冲蚀速率比非连通状态下降23.9%。

6.2流速差为4 m/s时

流速差为4 m/s时，管线连通情况下，6根注入管线的入口速度分别输入表2中的出口速度；对比分析组，即管线非连通的情况下，注入管线的入口速度分别输入表2中的入口速度，数值计算结果如图8～9所示。

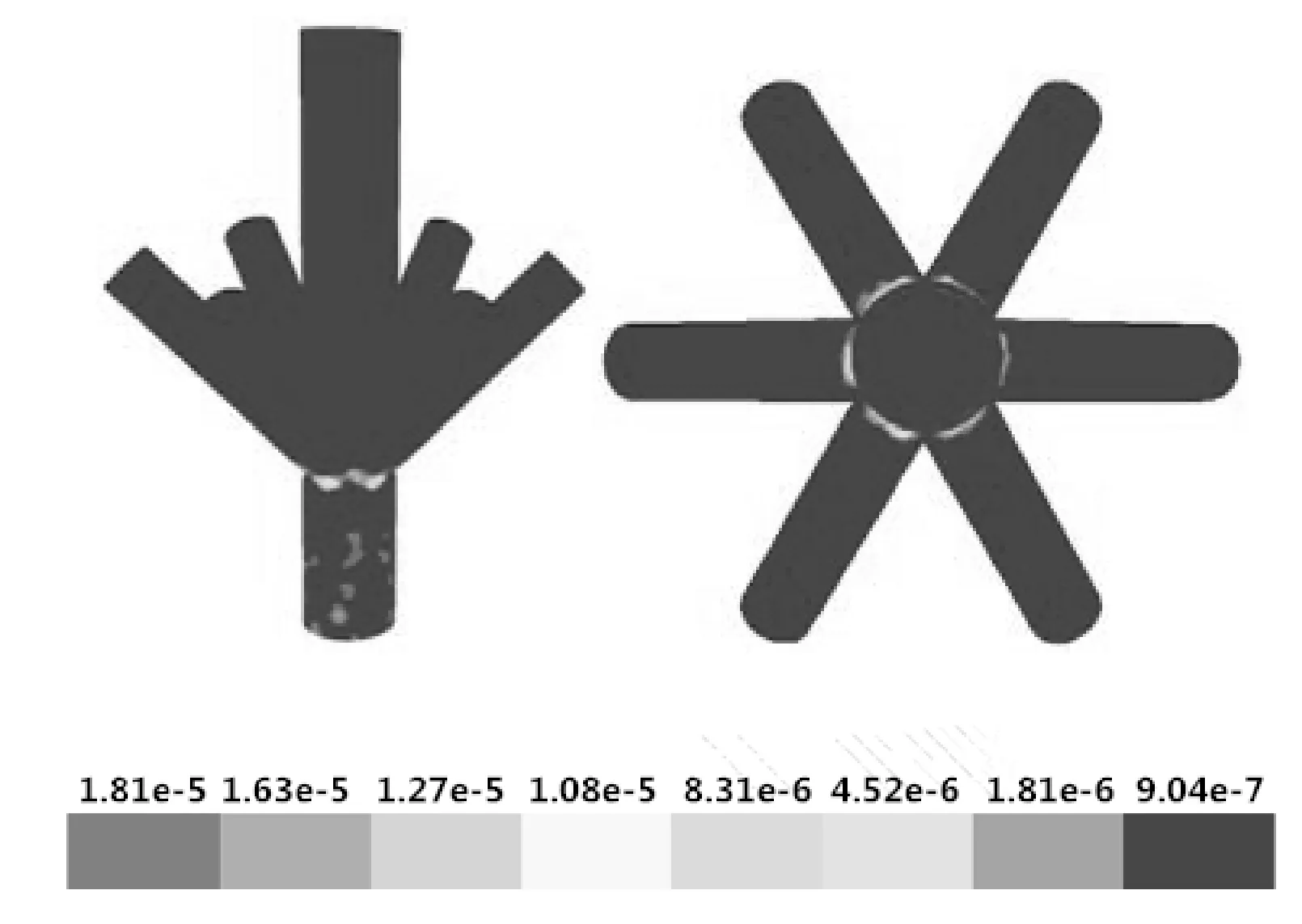
图8　流速差为4 m/s注入管线连通时井口八通注入头的冲蚀云图

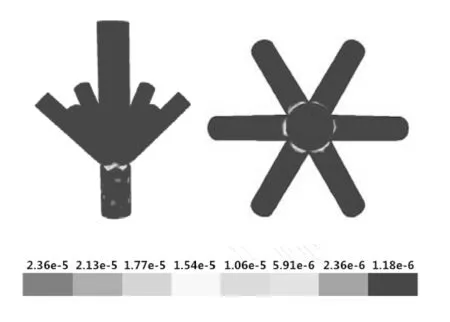
图9　流速差为4 m/s注入管线非连通时井口八通注入头的冲蚀云图

由计算结果可以看出，6根注入管线连通时井口八通注入头最大冲蚀速率为1.81×10-5kg/(m2·s)，6根注入管线非连通时井口八通注入头最大冲蚀速率为2.36×10-5kg/(m2·s)，注入管线连通时井口八通注入头最大冲蚀速率比非连通状态下降23.30%。

6.3流速差为2 m/s时

流速差为2 m/s时，管线连通情况下，6根注入管线的入口速度分别输入表3中的出口速度；对比分析组，即管线非连通的情况下，针对注入管线分别输入表3的入口速度，数值计算结果如图10～11所示。

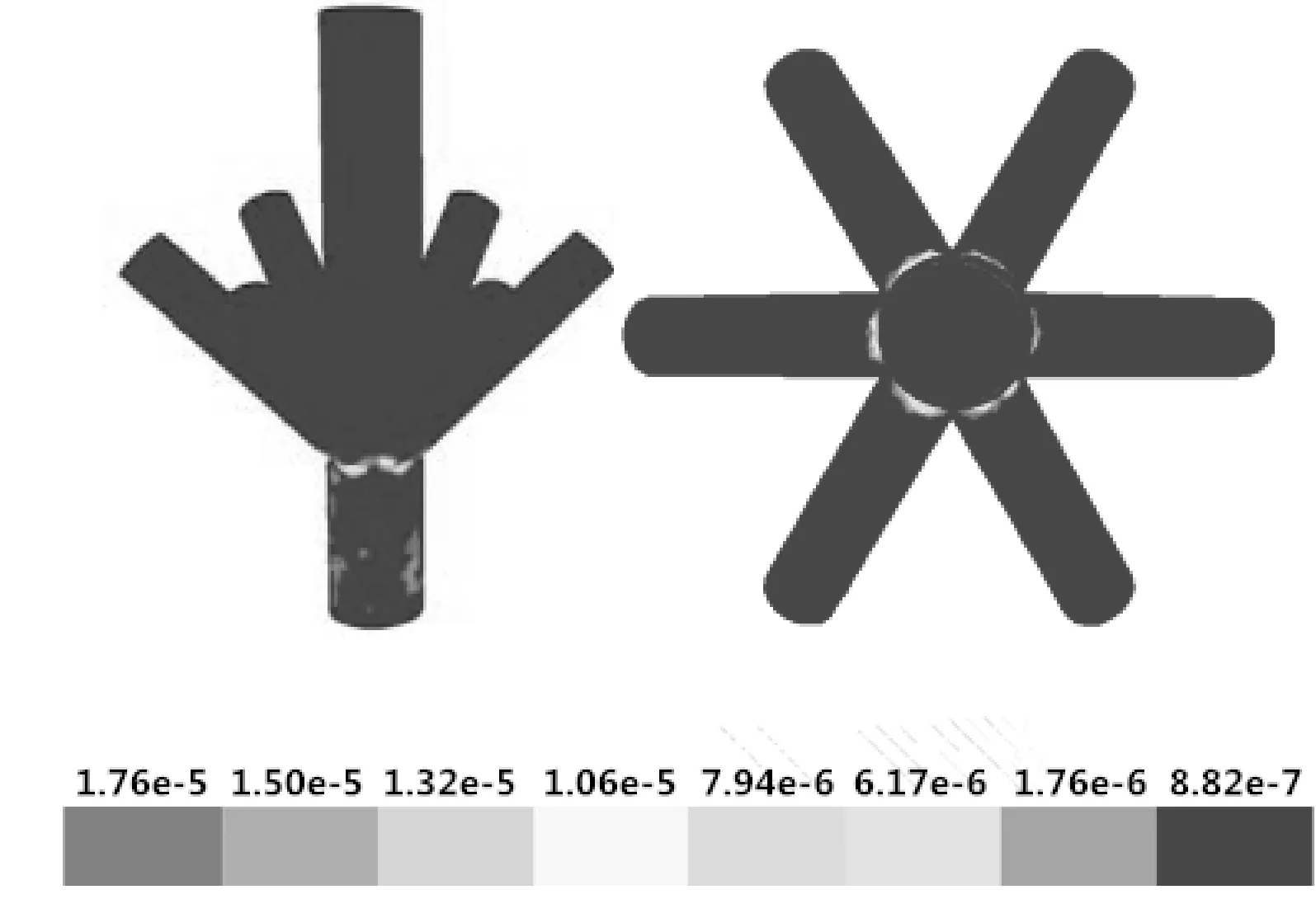
图10　流速差为2 m/s注入管线连通时井口八通注入头的冲蚀云图

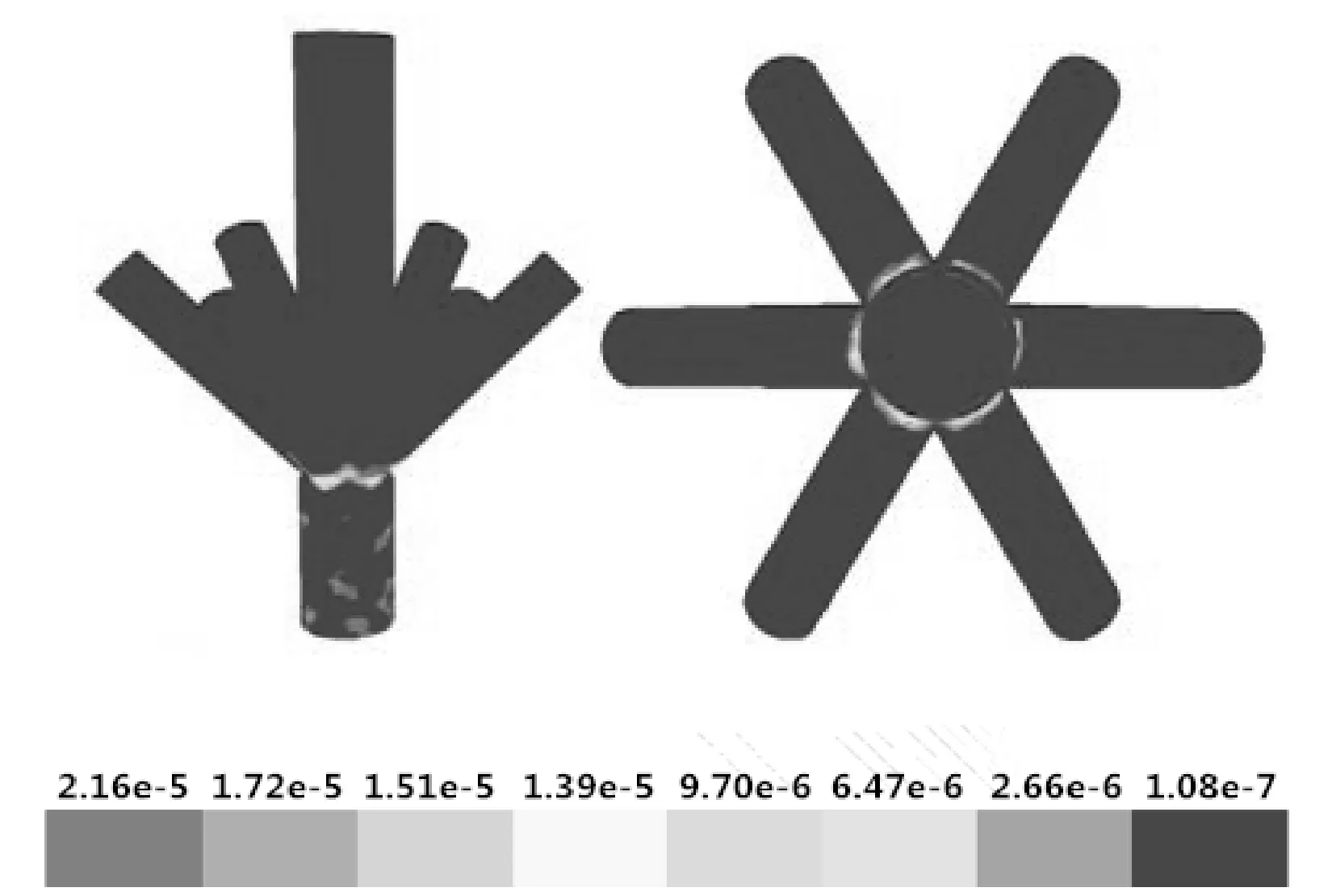
图11　流速差为2 m/s注入管线非连通时井口八通注入头的冲蚀云图

由计算结果可以看出，6根注入管线连通时八通注入头最大冲蚀速率为1.76×10-5kg/(m2·s)，6根注入管线非连通时井口八通注入头最大冲蚀速率为2.16×10-5kg/(m2·s)，注入管线连通时井口八通注入头最大冲蚀速率比非连通状态下降18.5%。

分析对比上述3组速度组的注入管线连通与非连通对井口八通注入头冲蚀磨损的影响可以看出，6根注入管线在非连通状态下，压裂液对井口八通注入头的冲蚀磨损都较大，这是因为6根注入管线中有两两相对的3对管线，注入管线非连通时相对的2根注入管线之间的流速差较大，在对冲后速度较大的一根注入管线较相对的另一跟注入管线的速度仍然较大，压裂液中支撑剂颗粒将会更多的向注入管线与注入头连接部位富集，进而对连接位置产生较大的冲蚀磨损。并且由于注入管线中压裂液流体的流速差较大，6根注入管线汇聚后流场的不稳定性增大，进一步加剧了压裂液对井口八通注入头的冲蚀磨损。而6根注入管线连通后，相对的2根注入管线由于速度大小相差较小，对冲后压裂液流体流速较小，汇流后的压裂液流体有沿井口八通注入头主管线流动的趋势，减小对井口八通注入头与注入管线连接部位的冲蚀磨损。并且在一定流速差范围内，流速差越大，6根注入管线的连通对减小井口八通注入头冲蚀磨损的作用越明显。

7结论

1)无论有无流速差，井口八通注入头的最大冲蚀速率均发生在6根注入管线与八通注入头主管线连接部位；6根注入管线中压裂液流体存在流速差时，提高了井口八通注入头的冲蚀速率峰值，使八通注入头的冲蚀磨损加重。

2)在一定流速差范围内，6根注入管线的连通可以降低流速差，且当6根注入管线的入口流速差越小时，6根注入管线的连通对流速差的降幅越明显。

3)通过对6根注入管线的连通可在一定程度上降低压裂液对井口八通注入头的冲蚀磨损，进而提高其使用寿命。建议在施工条件允许的情况下，将6根注入管线与井口八通注入头汇流之前进行连通，减缓井口八通注入头的冲蚀磨损，提高井口八通注入头的使用寿命。

参考文献：

[1]岳江河，肖乔刚.美国德州Eagle Ford组页岩油气水平井钻井关键技术措施及其实施效果[J].中国海上油气，2014(1)：78-81.

[2]钱斌，张俊成，朱炬辉，等.四川盆地长宁地区页岩气水平井组“拉链式”压裂实践[J].天然气工业，2015(1)：81-84.

[3]董大忠，高世葵，黄金亮，等.论四川盆地页岩气资源勘探开发前景[J].天然气工业，2014(12)：1-15.

[4]陈桂华，祝彦贺，白玉湖，等.页岩油气水平井井组地质油藏设计流程及其应用[J].中国海上油气，2013(6)：109-114.

[5]叶登胜，李建忠，朱炬辉，等.四川盆地页岩气水平井压裂实践与展望[J].钻采工艺，2014(3)：42-44.

[6]艾志久，孟璋劼，柴希伟，等.整体式Y型采气井口装置冲蚀规律及量化计算[J].科技导报，2015(11)：54-58.

[7]汪爽，倪超，严梦姗.气体钻井井口装置冲蚀规律研究及优化配置[J].钻采工艺，2014(5)：8-12.

[8]张广东，陈科，张旭，等.川东北高温高压高产含硫气井井口装置的优选[J].油气井测试，2011(4)：59-62.

[9]Patankar S V.Prediction of turbulent flow in a curved pipes[J].J.Fluid Mechanices，1975，7(3)：83-95.

[10]Jiang Luo，Budugur L.Prediction of strongly curved turbulent duct flows with Reynolds stress model[J].AIAA j，1997(35)：91-101.

文章编号：1001-3482(2016)07-0013-07

收稿日期：①2016-01-08

基金项目：国家自然科学基金项目“气体钻井钻具与井壁碰摩机理及量化评价方法研究”资助(No.50804040)；石油天然气装备教育部重点实验室项目(OGE201403-17)

作者简介：邹凤彬(1990-)，男，山东日照人，硕士研究生，主要从事油气田地面工程技术研究，E-mail：1207893960@qq.com。

中图分类号：TE931.107

文献标识码：A

doi：10.3969/j.issn.1001-3482.2016.07.003

Effects of Fracturing Fluid Velocity Contrast on the Erosion Wear of Wellhead Eight-way Injector Head

ZOU Fengbin1，QIU Yaling1，ZU Baohua2

(1.CollegeofMechanicalandElectricalEngineering，SouthwestPetroleumUniversity，Chengdu610500，China；2.No.1ConstructionCompany,ChinaPetroleumPipelineBureau,Langfang065000,China)

Abstract：For shale gas“wells factory” zipper fracturing construction of high pressure，large displacement，wellhead eight-way injector head has six injection pipelines，under the action of high-speed fracturing fluid is used to send severe erosion wear.Based on liquid-solid two-phase flow dynamics and erosion theory，the wellhead eight-way injector head erosion wear model is established，Then this model was applied to study how the velocity contrast effect the erosion wear of wellhead eight-way injector head of shale gas fracture.The studies demonstrated that the maximum rate of wellhead eight-way injector head erosion occurred in the area where the injection pipeline and the injection head connected to the main line；within a certain range，the greater the velocity contrast，the greater the erosion rate of wellhead eight-way injector head，can by injection pipeline connected to reduce the velocity contrast，to achieve the purpose of reducing the erosion rate of wellhead eight-way injector head.The research results provide a reference for reducing the erosion wear of the wellhead eight-way injector head.

Keywords：shale gas；zipper fracturing；injector head；erosion wear；numerical simulation