多元反算法研究滑坡抗剪强度指标的线性区域及其工程分析

韩仁生，冯乾朔，顾会男，王述红

(东北大学 资源与土木工程学院，辽宁 沈阳 110819)



多元反算法研究滑坡抗剪强度指标的线性区域及其工程分析

韩仁生，冯乾朔，顾会男，王述红

(东北大学 资源与土木工程学院，辽宁 沈阳 110819)

摘要：在分析滑坡灾害中，确定稳定系数及相关强度指标的取值是理论分析和数值计算成功的关键。本文利用极限平衡理论，根据边坡工程地质条件和结构面发育情况，假设相似的若干最危险滑动面，建立边坡滑坡体极限平衡方程，联立求解。同时，利用线性规划，得出某类边坡的边坡抗剪强度指标的变化范围，再结合经验和规范约束的C值和φ值范围，合理地在抗剪强度指标变化区域内，多次反算逼近，得出最精确的边坡抗剪强度指标，并对工程边坡的处理提出建议。

关键词：多元反算法；不平衡推力法；抗剪强度；边坡稳定性；极限平衡理论

1引言

对滑坡进行分析时，在可能产生折线或曲线滑动的危险滑动面的分析计算中，通常采用传递系数法。传递系数法适用于大部分的推力式滑坡，但对于牵引式滑坡，有时会出现下滑力与稳定系数相矛盾的情况[8]。于是，找到一种修正传递系数法误差的方法是很有必要的。

反算法是一种基于极限平衡原理的边坡反分析法，它是在极限平衡原理的基础上，假定滑坡体处于极限平衡状态，根据建筑边坡规范和经验得出边坡稳定安全系数K，得出粘聚力C或内摩擦角φ的变化范围，但一般的反算法对于抗剪强度指标的选择存在很大的误差和较大的不确定性，所以本文采用多元反算法与线性规划相结合的思想，目的在于得出抗剪强度指标的某一线性区域，并对其做出工程分析。

2多元反算法的基本思路

反算法通常采用传统条分法(即库伦理论)的各种演算公式，一般为传递系数法，即将地质剖面上的单宽滑体分为若干条块，由滑体后部逐条向前部计算，直至最后一块滑体。传递系数法假定上一块滑体传递下来的推力平行于上一块滑体的底滑面，且最后一块滑体的剩余下滑力等于或接近于零。要正确地运用反算法，就要选择滑动前瞬间极限平衡断面，此时滑坡稳定性系数为K。为了得到最恰当的K值，需要选取不同的计算剖面，进而得到不同的抗剪指标。这时，采用多元反算法，将数据利用图像表示，得出抗剪强度指标线性规划区域。再通过在合理范围内调整安全系数K，在相同的剖面上分析反算，对线性区域做进一步的修正完善，最后得出最优的抗剪强度指标变化区域，并由此分析出边坡的稳定性情况。

3多元反算法的计算公式

反算的方法不同，得到的强度指标也各不相同。我国广泛运用不平衡推力传递法来分析滑坡稳定。将滑坡体分为若干条块，假定条间力的合力与上一条土条底面相平行，根据力的平衡条件，逐条向下推求，直至最后一条土条的推力为零。已滑动过的滑坡，在其上一次滑动或近期滑动处，即将要滑动而尚未滑动时，是处于极限平衡状态的。在其上所取的断面，应属于极限平衡状态的断面。据此断面建立的推力计算公式中最后一条土条的剩余下滑力应等于零，即：

其中：

ψj=cos(θi-θi-1)-cos(θi-θi-1)tanφi+1

Ri=(Nj-ui)tanφi+ciLi

Ni=wicosθi

Ti=wisinθi

式中，ψi为传递系数；Fs为稳定系数；wi为第i块段滑体所受的重力(kN/m)；Ri为作用于第i块段的抗滑力(kN/m)；Ti为作用于第i块段的滑动分力(kN/m)；Ni为作用于第i块段的滑动分力(kN/m)；Ci为第i块段土的粘聚力(kPa)；θi为第i块段土的底面倾角(°)；φi为第i块段土的内摩擦角(°)；Li为第i块段滑动面长度(m)。

滑坡推力计算公式为：

Ei=Kiwisinαi+ψiEi-1wicosαi-CiLi(2)

式中，αi为第i块地下水流线平均倾角(°)；Ei为第i块剩余下滑力(kN/m)；Ei-1为第i-1块剩余下滑力(kN/m)；Ki为安全系数；其余参数同前。

令滑坡下滑力E=0，得到一个二元一次方程。假定一个合理的C值(或φ)，解得此时的φ值(或C)，重复几组计算，然后分别用假设的C和φ的范围代入公式，即确定多个临界滑坡体极限平衡状态的断面的抗剪强度指标，利用方程联立求解绘制C-φ关系图，得出抗剪强度指标的线性规划区域。

取3个断面的方程组为：

(3)

式中，W与式(2)中w相同。

方程组满足的条件：

(1)安全系数K经由建筑边坡规范和经验得出，即方程经迭代后，只有C和φ两个未知数。

(2)同一滑坡体，若发生多次滑动，其滑动面位置基本不变时，则按三次滑动距主轴断面距离相等分别建立的三个方程可以联立;其他断面对应两次滑动所建立的方程可以联立。

(3)不同滑坡体，若滑坡土体的性质类似，影响其强度变化的因素也相同时，可以选取一个滑坡体的主轴位置和另一个滑坡体沿主轴对称的滑动面建立方程。

建立联立方程的条件，一般在滑坡的产生和发展过程中比较容易找到，不仅局限于上述几种情况，只要遵循这样一个基本原则即可。

通常，当滑坡处于极限平衡状态时，任意给定一个C或φ值，由方程组可求得一个相应的φ或C值。因此，可分别求解出每个断面在极限平衡状态时的数对C、φ值。将两个不同断面的这些对C、φ值分别绘制强度指标，得到3条相交C-φ值曲线，组成线性区域，可以用于边坡处理的规划和建议。

下面结合工程实例，具体给出分析步骤、相关参数假设方法和结论验证方法。

4多元反算法的工程应用

建兴高速公路第七合同段(如图1和图2所示)位于建昌县的东北方向40km处，处于阴山纬向构造体系中、东段与大兴安岭-太行山新华夏构造体系东缘的交接部位，地质构造十分复杂，按构造体系可分为东西向构造、北东向构造、北北东向构造、南北向构造。受构造影响，区内断裂较为发育，以东西向和北东向断裂为主。项目存在区域断层F42，从K50+850附近通过。通过调查及钻探可知，该处灰质灰页岩历史上受构造影响，破碎后重新成岩，方解石重新结晶现象，层理节理裂隙发育，浅部存在溶蚀现象。

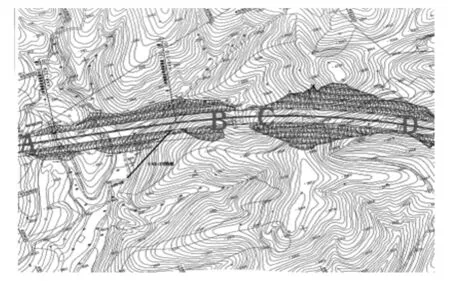
图1　建兴高速公路第七合同段地形图

该合同段中，K50+000-K51+000处为设计对象，该段边坡长约1000m，高-10.0m-40.0m，坡向约为45°-80°，平整后边坡坡面整齐。根据坡体开挖高度不同，将边坡分3段：AB段为岩土质边坡，上覆填砂土土厚2.0-4.5m，下覆中风化砂岩、页岩和微风化花岗岩，该段边坡长约600m，高6.0-20.0m，坡向60°；BC段边坡为填方边坡，边坡长约100m，高-10.0-4.0m；CD段为岩土质边坡，上覆土层厚2.0-4.5m，下覆中风化砂岩，该段边坡长约300m，高4.0-40.0m，坡向68°。

场地岩层单斜产出，岩层产状(即岩层的产出状态，由倾角、走向和倾向构成)为135°∠72°(倾向为135°，倾角72°)，层面裂隙间距0.5-1.0m，微张1-3mm，泥质充填，结合很差。场地岩体中发育有两组构造裂隙：J1产状为130°∠14°，裂隙面较平直光滑，间距0.3-0.5m，微张0-2mm，泥质充填，延伸2-5m，结合很差，为软弱结构面。J2产状为240°∠56°，裂隙面较平直光滑，间距0.6-1.0m，微张1-4mm，无充填，延伸1.5-3m，结合很差，为软弱结构面。

图2　K50-K51桩号地形剖面图(右上)

选取本工程中K50+200-K50+300段100m长的边坡进行滑坡体稳定性分析，该滑坡体滑面近似看作折线形。结合该边坡段的历史滑动情况，根据不平衡推力法的强度储备计算方法和当地经验，选取安全系数K=0.95，取滑动面的左右边界，联立多元反算法方程反算求解，得C和φ值的关系曲线图，如图3和图4所示。

图3　滑坡滑动时的C-φ关系曲线

图4　滑坡滑动时的C-φ关系曲线

对滑动面左右边界的C-φ关系曲线所得的两个三角形线性区域，取互相重合的部分，作为该滑动面的抗剪强度指标最佳线性区域，区域如图5和图6所示。

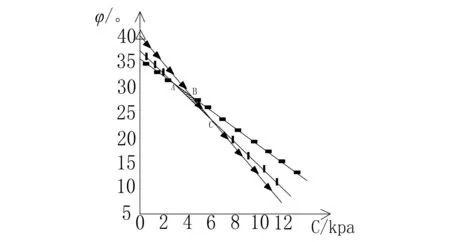
图5　滑坡滑动时的C-φ关系曲线

图6　线性区域放大示意图

如图所示，所得的三角形区域即为该目标路段进行反算分析时，粘聚力和内摩擦角假设的最佳取值的范围。

使用该方法进行二次反算分析，若C和φ值无其它约束条件，取区域的中心点对应的C和φ值为该路段土体的抗剪强度指标。

若C和φ值有线性约束，结合该区域取交点作为最终值，无交点时取线性区域到C-φ直线的距离最短的点对应的C和φ值。

若C和φ值关系曲线与线性区域可以围成二次图形，取新图形的中心点对应的C和φ值作为该路段土体的抗剪强度指标。

本工程中，C和φ并无其他约束条件， 故可以取线性区域的中心点对应值为最终值， 即可得C=4kPa，φ=28°，对该结果进行二次反算分析，结果在误差允许范围内，故可认为C=4kPa，φ=28°可以作为该工程的抗剪强度指标值。

5结语

综上所述，在滑坡体的稳定性分析与工程应用中，要确定抗剪强度参数，反算法填补了试验法和经验数据法的缺陷，成为一种比较有效的方法。而多元反算法得出具有理论意义的线性区域，结合C和φ值的其余约束条件，运用科学的线性规划分析法，得出抗剪强度指标的最优值，解决了传统反算法假设阶段的盲目性和反复验证阶段的复杂性问题。下一步可通过计算机研发相关的软件，使多元反算法更加简便和高效，并可对输出的线性区域，应用MATLAB等软件进一步验证结果的准确性和合理性，并应用于实际边坡工程。

致谢：本文得到东北大学土木工程专业吴宏的帮助和支持，在此致谢。

参考文献

[1]李凡,孙四平.多维图解反算法确定膨胀土滑坡土体的抗剪强度指标[J].岩石力学与工程学报,2004,23(6):1-7.

[2]徐汉斌，王军.反算法中滑坡稳定系数的取值问题[J].四川地质学报,1999,19(1):1-3.

[3]高丽娜，严明.反算法在某边坡稳定性评价中的应用[J].水土保持研究,2006,13(4):1-3.

[4]倪勇.建兴高速公路第七合同段边坡工程设计及稳定性分[C].2013,6:1-13.

[5]RoaSM，ReddyBVV，MuttharamM.Theimpactofcyclicwettinganddryingontheswellingbehaviourofstabilizedexpansivesoils[J].EngineeringGeology，2001，60:223-233.

[6]陈希哲.土力学地基基础[M].北京：清华大学出版社，2004.

[7]李晶岩，付丽.边坡稳定性分析方法[J].山西建筑，2011，37(2).

[8]MorgenstemN，PrieeVE，TheAnalysionoftheStabilityofGeneralSlipsSurface[J].Geotechnique,1965，15(1):80-95.

[9]王述红，张靖杰，李云龙，等.工程岩体开挖过程全空间块体搜索及其系统研制[J].东北大学学报(自然科学版)，2010，31(7):1024-1029.

[收稿日期]2016-06-13

[作者简介]韩仁生(1994-)，男，湖北省宜城人，东北大学本科在读。

[基金项目]东北大学国家大学生创新实验项目(150034)；国家自然科学基金(51474050；51179031；51074042)；地质灾害防治与地质环境保护国家重点实验室(SKLGP2012K009；SKLGP2014K011)。

中图分类号：U416.1+63

文献标识码：B

doi：10.3969/j.issn.1674-3407.2016.02.007

Using Multidimensional Back Calculation to Study Liner Range of Shear Strength of Slope and Engineering Analysis

Han Rensheng, Feng Qianshuo, Gu Huinan, Wang Shuhong

(School of Resource and Civil Engineering, Northeastern University, Shenyang 110819, Liaoning, China)

Abstract：The key of theoretical analysis and numerical calculation in landslide disaster analysis is to determine the best value of stability coefficient and relative strength index. According to the slope engineering geological conditions, the developmental condition of structural plane and some assumed dangerous sliding surface, the limit equilibrium theory is used to establish the equilibrium equation of slope landslide. According to the linear programming, the variation range of shear strength of a certain slope is concluded. Then, the range of C and φ is inhibited by experience and criterion. The more precise shear strength is concluded by several back calculations in the variation range of shear strength. At last, the suggestions on engineering of slope treatment are proposed.

Keywords:multidimensional back calculation; imbalance thrust force method (ITFM); shear strength; slope stability; limit equilibrium theory