一种压电陶瓷双晶片压痕响应的试验研究

曾思远，王煜天

(1.吉林大学机械科学与工程学院工业工程系，吉林 长春 130000；2.长春理工大学机电工程学院，吉林 长春 130000)



一种压电陶瓷双晶片压痕响应的试验研究

曾思远1，王煜天2

(1.吉林大学机械科学与工程学院工业工程系，吉林 长春 130000；2.长春理工大学机电工程学院，吉林 长春 130000)

摘要：在对纳米压痕测试基本原理及性能特点进行分析研究的基础上，针对一种典型压电双晶片开展了压痕响应测试分析，测得了不同最大压入载荷条件下的载荷-压入深度关系曲线，得到了材料的硬度与最大压入载荷间的关系。本文对分析研究压电材料及其器件的力学性能具有借鉴意义。

关键词：压电双晶片；纳米压痕；力学性能；压痕曲线；硬度

1引言

压痕测试技术又被称为深度敏感压痕技术，是通过检测系统拾取压头压入试验样品的压入载荷与压入深度，从而通过载荷-压深曲线测定材料的弹性模量与硬度等基本参数[1-3]。由于压痕测试技术具有测试过程简便灵活、试样制作简单、测试精度高、测试材料力学参数种类丰富等优点，近年来已发展成为材料力学性能测试的主流技术之一，广泛应用于航空航天、信息通信、光电子、纳米工程、微机电系统和纳米摩擦等领域材料微观力学性能的测试分析中[1]。

2压痕测试基本理论方法

压痕测试中，通过仪器内置的检测单元可直接拾取压入深度h与压入载荷P。依据Oliver和Pharr等人总结提出的接触刚度-接触深度方法，通过载荷-压入深度曲线的卸载段可测定材料的硬度与弹性模量[2-5]。图1为压痕测试曲线的基本构成。

图1　压痕测试曲线的基本构成[5]

加载阶段，试件材料在压头作用下首先发生弹性变形。随着压入载荷的增加，材料逐渐发生塑性变形，使加载曲线呈现出非线性特性。卸载阶段，随着压头脱离试件表面，试件材料会发生弹性恢复。图1中，P和h分别代表压入载荷与压入深度，定义Pmax为最大压入载荷，hmax为对应最大压深，hf为残余压深，S为接触刚度[2-5]。

可采用以下函数拟合载荷-压深曲线的卸载段。

P=k(h-hf)n

(1)

式中，k和n为拟合参数。

在此基础上，定义接触刚度为曲线卸载起始点的斜率，有：

(2)

接触深度hc可表示为：

(3)

其中，ε是与压头形状相关的常量。定义Ap为压头与试件材料的接触区投影面积，有Ap=f(hc)。

可得试件材料的硬度H，可表示为：

(4)

进而可推导出试件材料的弹性模量E为：

(5)

其中，Er为折算模量，是由被测材料的弹性模量E和泊松比v以及压头材料的弹性模量Ei、压头材料的泊松比vi综合确定的。

3压电双晶片压痕试验测试

压电材料由于其压电效应，在精密传感器、智能发电、噪声与振动控制等领域被广泛应用；又由于其具有逆压电效应特性，在精密驱动定位领域展现出良好的应用前景。本文以一种PZT压电陶瓷双晶片作为被测对象，采用压痕仪器开展了压痕响应测试分析，压头材料为单晶金刚石，以压入载荷作为控制量。

图2为最大压入载荷Pmax=200mN时，压电陶瓷双晶片材料的压痕响应曲线。通过分析压痕曲线可发现，此时压电陶瓷双晶片整体表现出较好的弹塑性特性，结合前述理论方法可得此时的接触深度为1.81μm，整体的硬度为2.49GPa。

图2　最大压入载荷200mN时压电双晶片的压痕曲线

图3为最大压入载荷Pmax=500mN时，压电陶瓷双晶片材料的压痕响应曲线。通过分析压痕曲线可发现，此时压电陶瓷双晶片整体表现出较好的塑性特性；随着压入载荷的增加，其弹性回复性显著削弱。此时的接触深度为2.73μm，双晶片整体硬度为2.73GPa。

图3　最大压入载荷500mN时压电双晶片的压痕曲线

通过一系列的压痕测试，得到不同最大压入载荷下压电陶瓷双晶片整体硬度的测试结果，如图4所示。从图4的试验结果可以发现，材料硬度随最大压入载荷的增加而呈现出波动状态，其原因主要在于压电陶瓷薄片与铍青铜材料粘结的均匀性差异，导致不同压入位置材料性能会产生一定的变化。

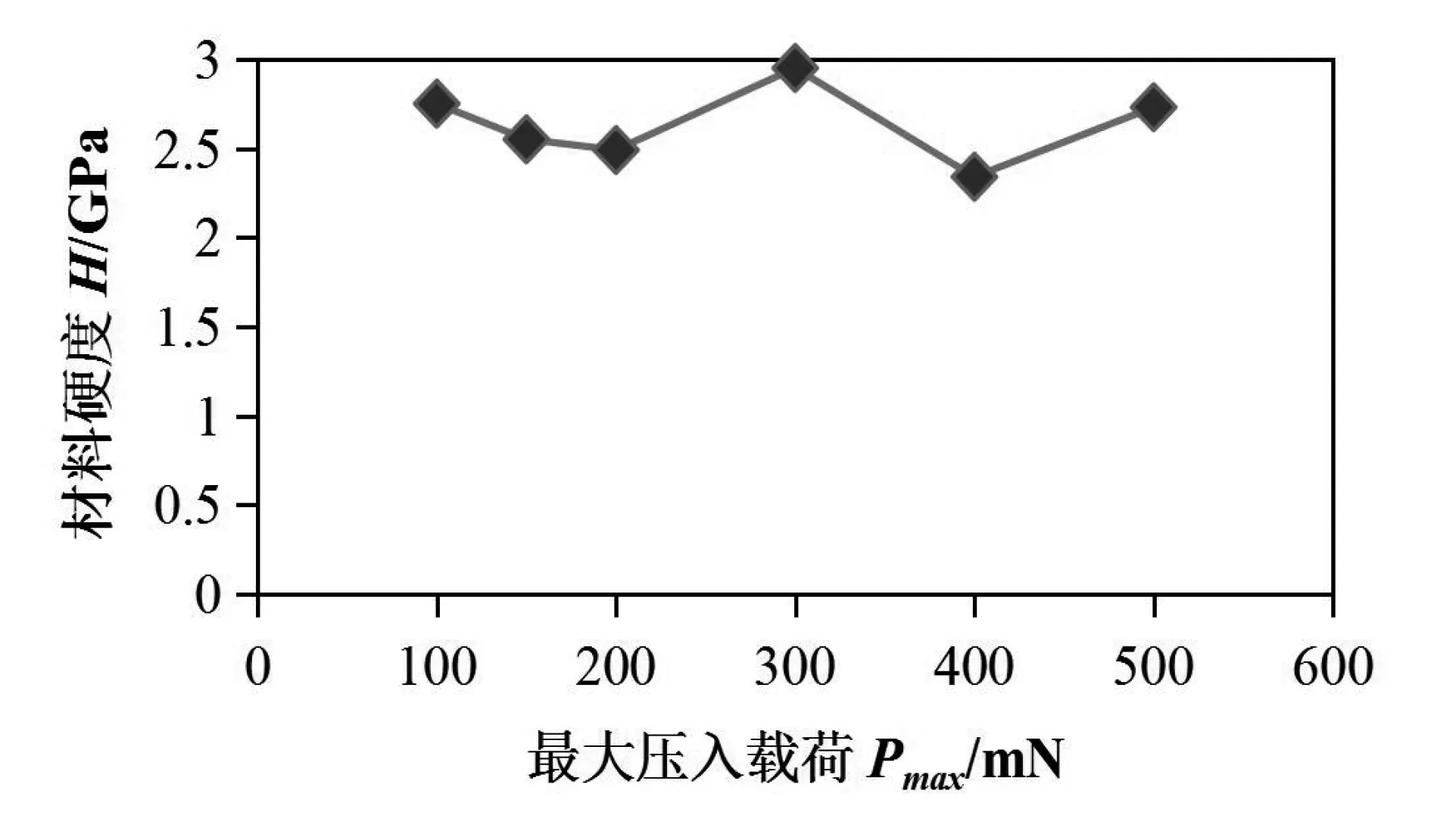
图4　压电双晶片硬度值与最大压入载荷的关系

4结论

本文对压痕测试基本原理、优点与应用领域进行了分析， 在此基础上，针对一种典型压电双晶片开展了压痕响应的测试分析，得到了不同最大压入载荷下的载荷-压入深度关系曲线。结合压痕测试基本理论，得到了压电双晶片整体的硬度，发现硬度随最大压入载荷的变化呈现出一定的波动，结合对压电双晶片整体结果的分析，认为导致这一现象的原因在于材料整体不均匀性。

参考文献

[1]黎明,温诗铸.纳米压痕技术理论基础[J].机械工程学报,2003,39:142-145.

[2]OLIVER W C, PHARR G M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation measurements[J]. Journal of Materials Research, 1992,7:1564-1583.

[3]DOERNER M F N, NIX W D. A method for interpreting the data from depth-sensing indentation instruments[J].Journal of Materials Research,1986,1:601-609.

[4]PHARR G M, BOLSHAKOV A. Understanding nanoindentation unloading curves[J].Journal of Materials Research,2002,17:2660-2671.

[5]FISCHER-CRIPPS A C. Nanoindentation[M].New York: Springer-Verlag, 2004.

[收稿日期]2016-06-13

[作者简介]曾思远(1995—)，男，吉林大学机械学院工业工程系本科生，主要研究方向为机械结构优化设计与结构性能测试。

中图分类号：TN384

文献标识码：B

doi：10.3969/j.issn.1674-3407.2016.02.005

Study on Indentation Experiment for a kind of Piezoelectric Bimorph

Zeng Siyuan1, Wang Yutian2

(1.Department of Industrial Engineering, Jilin University, Changchun 130000, Jilin, China;2.College of Mechanical and Electric Engineering, Changchun University of Science and Technology,Changchun 130000, Jilin, China)

Abstract：The principle and characteristics of nanoindentation test are analyzed in the paper. Based on the analysis, the nanoindentation experiment for a kind of piezoelectric bimorph is carried out. For different maximum indentation load, the curves for the relationship between load and indentation depth are measured, and the hardness is tested. Based on these works, the relationships between hardness and maximum indentation load are analyzed. The research has important significance for analyzing the mechanical performance of piezoelectric materials and device.

Keywords:piezoelectric bimorph; nanoindentation; mechanical performance; curve of indentation; hardness