推力轴承系统流场分析

张培良，张 宏，吴军令

（水力发电设备国家重点实验室，哈尔滨 150040）

推力轴承系统流场分析

张培良，张 宏，吴军令

（水力发电设备国家重点实验室，哈尔滨 150040）

建立推力轴承流场有限元模型，对其进行有限元分析，求得流场的流态、速度及压力分布情况。为推力轴承性能计算提供边界条件。

推力轴承；FLUENT；流场分析

0 引言

研究推力轴承润滑及冷却系统内部的流场参数，对高速重载流体润滑推力轴承的结构设计和优化，确保电动机的安全运行都具有重要意义。旋转镜板与推力瓦之间的流体楔中润滑流体的内摩擦和流体槽中的流体被激烈搅拌而产生的热量使流体温升高，冷却器与这些热流体进行热交换使流体温度降低，流体槽中的流体流动情况直接影响流体与瓦以及流体与冷却器的热交换，进一步影响了瓦的温度分布，因此研究流体槽内部的流场，对推力轴承润滑参数的计算，特别是温度场的计算（最终是计算推力瓦的热变形）提供可靠的边界条件，对冷却器的正确设计和安装都具有重要意义。

推力轴承设计难度很大，不仅要重视瓦的支撑结构、瓦材料的选择、镜板加工精度的控制，同时推力轴承润滑流体的冷却方式及结构的研究也同样重要，推力轴承运行可靠性主要取决于瓦的支撑方式（减少瓦的机械变形）和润滑流体的冷却结构，使流体循环合理、散热效果好，同时降低瓦的热变形。所以研究轴承周边内部流场有很重大的意义。

1 轴承流场结构特点及有限元模型

根据机组结构立式布置的需要，整个推力轴承由上、下两组轴承组成，以便在机组启动和低速运转时主要承受方向向下的转子自重，在正常运转时主要承受方向向上的流体推力[1]。除此之外，它还要满足正、反向转动的要求。

流场结构如图1所示，流体从上轴承1处流入，沿径向方向流进飞轮与侧壁间隙，再从下轴承2处流出，从轴承间隙和瓦面流出。

图1 轴承结构

推力轴承内部流体的流动为三维定常不可压粘性流动。描述其流动的基本方程为质量守恒方程和动量守恒方程。本文计算中将旋转件表面转动线速度化为无量纲的单位1，流场最高压力也化为单位1，其余数值按比例。

推力轴承结构复杂、尺寸大，而推力轴承的流体膜是存在于推力轴承的镜板和瓦之间、长度和宽度以米来计、厚度却小于毫米的一个流场，所以间隙和1/6模型的网格直接划分则无法连接，这就需要进行网格搭接即构建一个间隙和1/6模型的搭接模型进行网格划分，在网格划分时对这三部分采用分块划分，即对间隙部分和剩余的整体部分采用结构化网格。

网格搭接的结果如图1所示，图2中3处为0.1mm厚间隙流场，4处为轴承周边流场。

图2 网格处理示意图

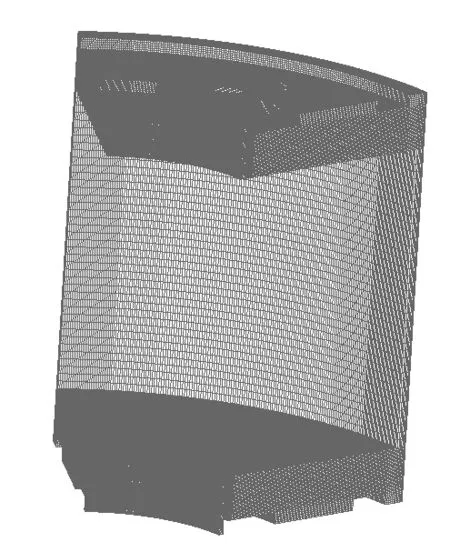
图3 流场整体网格

图4 轴承处流场模型网格剖视

边界条件：进口为速度进口边界条件用于给定进口的速度及其他相关标量值，进水口速度为0.014。因计算模型是整个流体槽的1/6，故计算模型的出、入口两侧满足周期性边界。采用标准模型；在转动部件与流体接触的边界，流体流的角速度是旋转部件的线速度为1，采用wall；除周期性边界、拖动边界外，模型其余边界为固壁，采用wall。

计算结果及分析整体流场的内表面的速度和轴与飞轮的转动线速度一致，最高速度为1，轴承周围流场流动速度在0.051左右[2,3]。

推力轴承高压区均位于流体进口边区域，压力从流体间隙进口处向内逐步递减，高压区压力1，低压为0.887。流体计算的时候液膜模型的厚度是常数，不同液膜厚度对应的压力不同。

图5 流场内壁速度分布

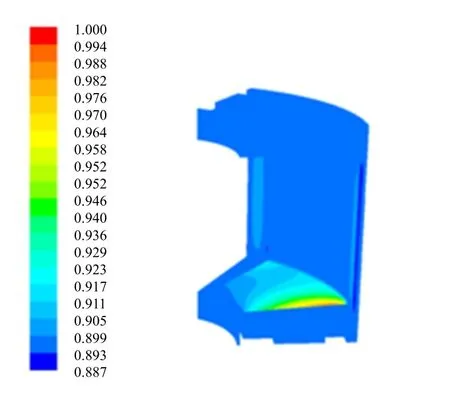
图6 压力分布

图5为流场与转动部件接触面的速度分布，图6为流场整体压力分布。图7为上轴承流体的迹线轨迹，图中4号和5号区域的周向截面速度分布见图8和图9。流场径向截面速度分布分别对应的是图10和图11。图12为下轴承流体的迹线轨迹。

图7 上轴承流体迹线（进流体）

由图9 可见，流体受到瓦身的阻碍，上下轴承均产生速度0.077垂直镜板运动方向的速度。

上轴承处的涡动速度大于下轴承处，因为上轴承处的离心速度与流体动方向相同为0.02，而下轴承处的离心速度与流体流动方向相反，为0.015。

转动部件运动产生的周向流碰到轴承阻挡时速度矢量方向改为垂直周向速度，因此形成了瓦面进口流体的旋涡。流体在瓦面出口侧由于飞轮的转速高。流体膜处液速流出，且飞轮面附近一定范围内流体速度较高，为了使出流体边的液体及时得到补充，就有液体向出流体边流动的分量，如图8所示。

图8 上轴承左侧流场速度分布（截面）

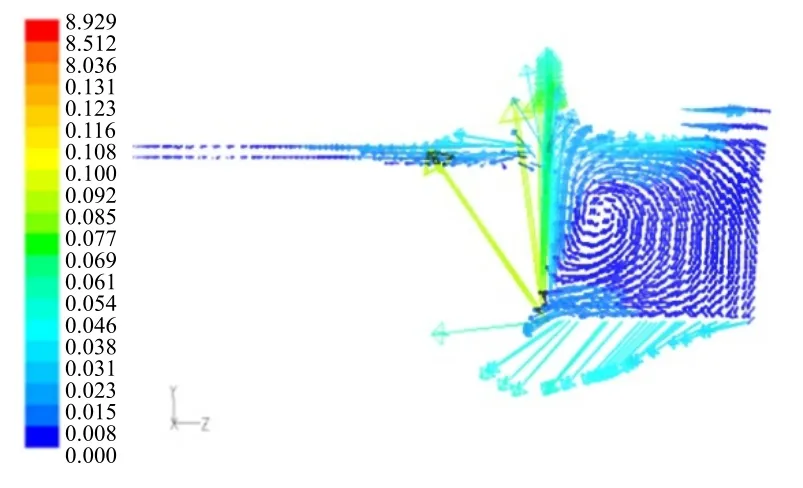
图9 上轴承右侧流场速度分布（截面）

图10 上推力轴承进流体侧

液体由很大的垂直分量，沿径向向外垂直速度增大到6m/s左右。

从上推力轴承进流体侧和出流体侧速度分布图可见，进流体侧由于瓦身的阻碍产生旋涡，上轴承处的速度矢量向下，对于下轴承处的速度矢量则向上。

3 结论

（1）建立了间隙流体润滑膜和轴承周边流场的全流场模型，并利用有限元软件求得了流场的压力、速度和流态。

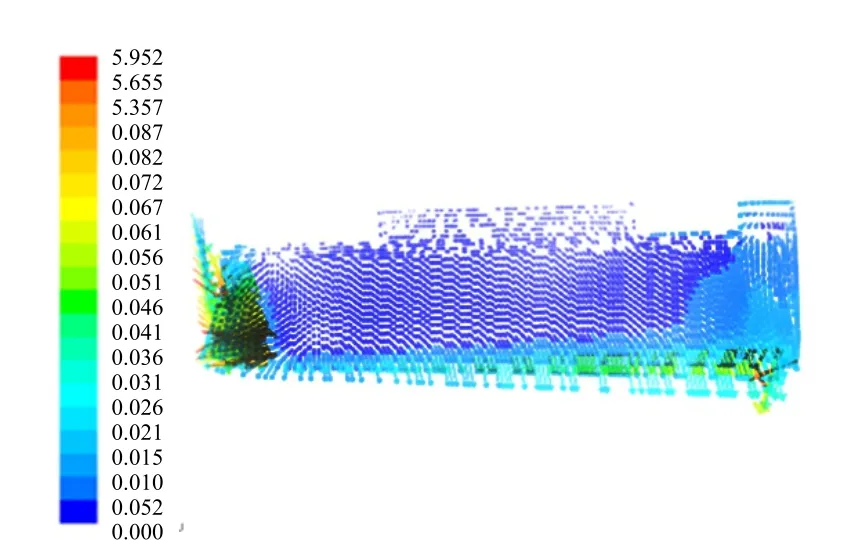
图11 上推力轴承出流体侧

图12 下轴承流体迹线（截面流态略）

（2）研究得出了轴承周边流场的流态与速度分布，进而可以得出轴承周边的对流换热系数。对轴承性能的有限元研究提供边界条件计算支持。

[1] 韩占忠, 王敬, 兰小平. FLUENT流体工程仿真计算实例与应用[M]. 北京理工大学出版社, 2004, 6.

[2] 李景惠, 李永海, 向敬忠. 推力轴承流体槽流体流态的可视性研究[D] .哈尔滨理工大学, 2000, 5(2): 5558.

[3] 张兆顺, 崔桂香, 许春晓. 湍流理论与模拟[M].清华大学出版社, 2005.

审稿人：武中德

FlowFieldAnalysisofThrustBearing System

ZHANG Peiliang, ZHANG Hong, WU Junling
(State Key Laboratory of Hydro-power Equipment, Harbin 150040, China)

Flow field of thrust bearing finite element model was established and the finite element analysis was executed, get the flow regime, velocity and pressure distribution of the flow field, providing boundary condition for thrust bearing performance calculation.

thrust bearing; FLUENT; flow field analysis

TM39

A

1000-3983(2016)02-0012-03

2015-07-11

张培良(1985-)，男，2010年毕业于哈尔滨工业大学机械工程专业，工学硕士，工程师，主要研究方向为发电机轴承技术。