B2C电子商务物流中心选址-路径综合优化研究

邓学平，周昔敏，田帅辉

(重庆邮电大学 经济管理学院，重庆，400065)



B2C电子商务物流中心选址-路径综合优化研究

邓学平，周昔敏，田帅辉

(重庆邮电大学 经济管理学院，重庆，400065)

摘要：为优化B2C(business-to-customer)电子商务物流系统，结合B2C电子商务特点，构建以物流成本最小为目标函数、以运输时间和供需关系限制为约束条件的电子商务物流中心混合整数规划模型，采用改进的遗传算法将电子商务物流中心选址的混合整数规划模型求解过程转换成求解最优运输路径问题，并且设置惩罚算子对超过运输时间限制的方案进行特定的惩罚处理，设计合适的染色体编码方式、交叉算子、变异算子、惩罚函数等。通过随机生成的数据运用Matlab软件进行算例仿真模拟，验证模型的有效性。

关键词：物流选址；路径优化；混合整数规划；遗传算法；电子商务

0引言

B2C(business-to-customer)电子商务线上交易的快速发展迫切需要构建线下高效的物流体系作为支撑。其中，物流中心选址是构建过程中的关键环节，对提高顾客服务水平、降低电子商务系统的物流成本具有重要的意义。

目前，国内外学者针对物流中心选址问题大多是以成本最小化或利润最大化为目标，以容量限制或者客户个性化需求等为约束条件的数学模型。文献[1]综合考虑库存成本、运输成本等因素建立了规划模型并进行求解；文献[2]建立了以成本最小化和效益最大化为目标的多目标规划选址模型，并设计混合启发式算法进行模型求解；文献[3]建立了电子商务物流配送中心的非线性规划选址模型，并运用启发式算法进行求解；秦固[4]提出了解决多物流配送中心选址问题的蚁群算法模型；吴筱娴等[5]提出了基于直觉模糊TOPSIS 方法的电子商务物流配送中心选址模型；张晓楠等[6]构建了以物流总费用为主目标函数，以配送中心流通费用、车辆派遣费用、配送费用总和为子目标函数，建立了有配送中心容量静态约束和车辆动态负载量约束的双目标模糊选址模型，设计了嵌入随机算法和禁忌搜索算法的遗传算法求解；关菲 等[7]建立了以物流总费用最少、物流配送中心综合服务水平最高为目标的模糊多目标物流配送中心选址模型，提出了多目标粒子群优化算法进行求解；过晓芳等[8]以最小化物流系统总费用和最大化物流服务水平为优化目标，建立了三级供应链模式下的物流配送多目标优化模型，并提出了基于偏好的多目标进化算法；胡琳等[9]构建了物流配送中心地址优化的双层规划模型，提出了改进的粒子群优化算法求解双层规划模型。从目前关于物流中心选址的研究来看，存在以下局限：1)结合电子商务物流呈现的客户多、分布广、品种多、批量小等具体特征，对电子商务物流的深入研究较少，尤其是涉及到具体的包裹配送；2)对物流中心选址的研究大多未和路径优化结合，而是研究单一的选址问题。基于此，本文以B2C电子商务为研究对象，将电子商务物流中心选址问题和路径优化问题结合起来，建立成本最小化的目标函数，以运输时间和供应需求关系为约束条件，建立混合整数规划模型，利用遗传算法将物流中心选址的混合整数规划模型求解过程转换成求解最优运输路径问题，从而优化电子商务物流系统。

1问题描述及模型

1.1问题描述

B2C电子商务物流中心选址问题可描述为：企业根据区域内各类商品的销售和供应情况，在已知满足其他选址原则且具备一定物流处理能力的几个备选物流中心中，寻找满足规定的电子商务物流需求的最佳选址方案，即寻找满足总成本最小、运输时间要求的备选物流中心，同时还能提供最佳供应地选择方案、运输路线方案。

具体实施过程是将系统中的各个点简化为供应地、物流中心和需求地，配送网络结构图如图1所示，供应地到需求地的包裹运输是多对多的关系。模型的目标函数是使总运营成本最小，包括固定成本费用、运作成本、运输成本和管理经营费用，约束条件为供应-需求关系和各包裹的运输时间。

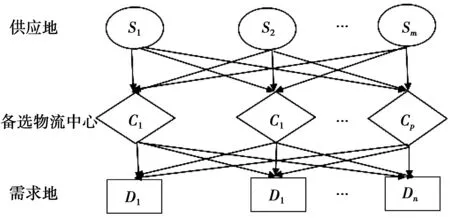
图1　运输网络模型Fig.1　Transportation network model

1.2模型假设

①备选物流中心都是合理可行的，运输周转、仓储容量、信息处理能力等都满足要求。

②实际情况中的包裹运输可能需要经过多个物流中心进行中转，为了简化模型，将包裹的运输路线进行分段截取处理，运输路线假设都为：Si-Ck-Dj。

③每条运输路线都是畅通无阻，没有因为意外交通事故、道路修建造成时间延误。

④供应地i到物流中心k的运输时间、物流中心k到需求地j的运输时间与包裹种类无关。

⑤供应地数目、需求地数目、备选物流中心数目、供应地到物流中心的运输费率、物流中心到需求地的运输费率、供应地的供应能力、需求地的需求量、备选物流中心的建设成本、单位包裹经物流中心的管理费用均为已知参数。

1.3参数定义

1.3.1已知参数定义

模型中各参数的含义如表1所示。

表1　参数定义

续表1

编号参数含义8bkjt表示包裹t从备选物流中心k运至需求地j的运输费率9rkt表示单位包裹t在第k个物流中心周转发生的管理费用10λik表示包裹t从供应地i到物流中心k需要的运输时间11λkj表示包裹t从物流中心k到需求地j需要的运输时间12λk表示包裹t从物流中心k需要的最大转运处理时间13λ't表示包裹t的规定运输时间天数要求14fk表示第k个物流中心的固定成本费用,主要包括土地成本、基础建设成本、设施设备成本

1.3.2决策参数定义

模型中决策参数说明如表2所示。

表2　决策参数

1.4目标函数定义

1)总运营成本最小目标函数为

(1)

(1)式中：等式右边第1部分表示包裹t从供应地i到物流中心k所需的运输费用；等式右边第2部分表示包裹t在物流中心k所需的运作成本和管理费用；等式右边第3部分表示包裹t从物流中心k到需求地j所需的运输费用；等式右边第4部分表示物流中心k的固定成本。

2)约束条件。

①需求地对包裹t的需求量等于对应单次运输量之和。

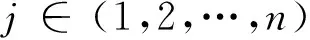
(2)

(3)

③各已知参数的取值范围。

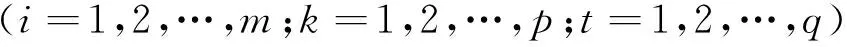
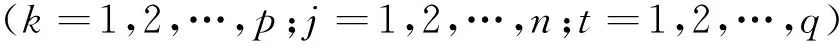
2模型求解

为适应电子商务物流中心选址问题，利用改进后的遗传算法进行求解。通过模拟自然进化过程搜索最优解[10]，将电子商务物流选址混合整数规划模型的求解过程转换成求解最优运输路径问题，将染色体编码方式转化为运输路线，用基因表示物流中心编号、包裹种类、供应地编号、需求地编号，产生初始种群；同时设置惩罚函数对超过运输时间限制的方案进行特定惩罚处理，计算目标函数值，得到个体适应度；再对群体进行选择、交叉、变异遗传运算，迭代若干次后，收敛于最优选址方案。

2.1编码方案

由于模型涉及参数较多，数值在实际应用中也较大，所以直接采用实数编码方式，使用各参数本身数值，减少计算量，全部数值类型均采用double类型。

1)基因编码。基因编码为{k|tjixikt|…|t′j′i′xi′k′t′}，具体含义及信息如表3所示，表示选择第k个备选物流中心，包裹t需要从供应地i向需求地j提供xikt个包裹。

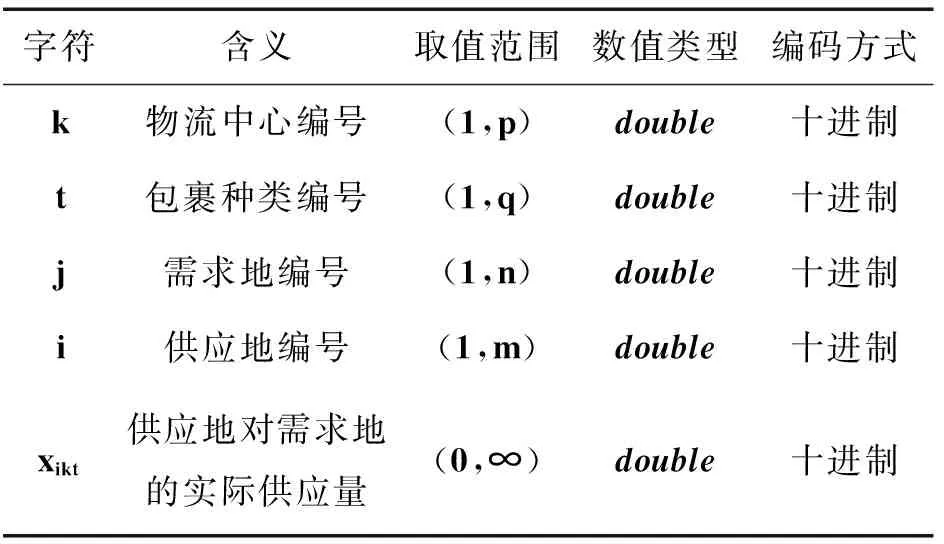
表3　基因编码

2)染色体由一个物流中心编号基因和q个大组基因组成，每个大组由n个小组组成，即第q个大组对应的小组为第(q-1)×(n+1)—q×n小组；同时每个小组由4个基因组成，分别表示：①每小组第1列为t，表示第t种包裹；②每小组第2列依次为1：n，表示需求地编号；③每小组第3列，根据第1、2列，如果需求地对包裹的需求量为0，则第3列为0；否则在商品对应的可选供应地编号中选择一个数字，且该供应地的供应量符合需求量。④每小组第4列，对应供应地对需求地的实际供应量。则染色体长度为popsize=4×需求地个数×包裹种类数目+1。算例的需求地数目为10，包裹种类为10，所以popsize=401。

2.2初始化种群

算例设置种群规模为popnumber=20。初始种群的生成步骤如下。

①初始化一个全为0的数组。

②令第一行第t个大组中的全部小的组第1个值为t，t=1∶q。

③令第一行每个大组的第2个数值依次为1∶n。

④根据每组第1，2列的数值，判断该需求地对该包裹的需求量是否为0；如果是，则第3列数值为0，否则在可选供应地所组成的数组中随机生成一个数值，判断该地的供应量是否满足需求量，如果不满足则重新生成随机数据，直到满足为止。

⑤根据第1，2，3列，如果需求地对包裹的需求量为0，则第4列也为0；否则，等于该供应地对需求地的供应量。

⑥采用循环方法，重复第②步—第⑤步，直到产生全部行列的数据。

2.3惩罚函数

为避免局部最优，需设置惩罚函数对其规定运输时间进行适当调整，扩大可选择范围，从而保证全局最优。惩罚函数可描述为：因为超过了规定运输时间，物流企业将付出一定的成本代价，这些代价可以是司机的加班费、机械消耗的费用、以及弥补客户满意度的费用等。惩罚函数调整过程如下 ：

①查找出总时长超过了规定时间的染色体，并计算其超出的时间之和Δλ。

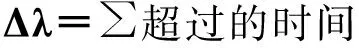
(4)

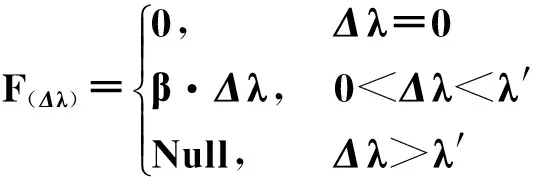
(5)

(4)—(5)式中：β为常数，表示每超出单位时间给企业所带来的费用损失；λ′为常数，表示Δλ最大可接受限度的时间；当Δλ=0时，即所有染色体片段都满足时间要求，惩罚函数值为0；当Δλ>0时，对其进行惩罚处理。

2.4适应度函数

G表示适应度，值越大表示该染色体的适应性越好。

(6)

(6)式中：max为一个足够大常数，算例中的max设置为530 000，w为混合整数规划模型中建立的目标函数，为惩罚函数。

2.5杂交与变异

2.5.1杂交

采用两点均匀杂交，不同父染色体之间随机选择两点进行互换，杂交率为0.4。

①随机产生2个不相同的正整数h1，h2∈[1,popnumber] ，确定第h1 和第h2条父染色体之间进行互换处理。

②随机生成一个正整数h3∈[1,n×q]，确定将第h3个小组的第3个数值进行互换。

③检查杂交后的染色体是否满足供应需求的约束条件，如果不满足，则返回第②步重新随机生成；若满足条件则进行数值交换。

2.5.2变异

设置变异率为0.01。

①随机生成正整数h4∈[1,popnumber]，确定第h4个子染色体发生变异。

②随机生成一个正整数h5∈[1,n×q]，如果h5所在的小组的第4个数值为0，则重新生成h5。直到满足条件后，确定第h5个小组的第3个数值发生变异。

③对第h4个染色体第h5个小组的第3个数值在对应包裹的可选供应地数组中重新随机生成，检查变异后的染色体是否满足约束条件，如果不满足，则返回第②步；若满足条件则进行数值交换，完成一次变异。

2.6遗传算法参数

①种群规模：种群规模的大小决定了种群的多样性，遗传算法中种群规模一般设为20—100，算例种群规模设定为20。

②交叉概率：交叉概率决定了群体中进行杂交的基因比例。交叉概率选择范围是0.4—0.99，算例设置交叉概率为0.4。

③变异概率：生物界中发生变异的情况很少，所以遗传算法确定的变异概率也很低，一般取值在0.001—0.01之间，算例选取变异概率0.01。

④迭代停止条件：终止条件一般是设定固定的进化迭代次数，算例设置最大迭代代数为50次。

3算例验证

3.1数据生成与处理

算例中所需数据是通过模拟电子商务自营物流模式中转运中心的实际情况，利用Excel随机产生。假设包裹种类数目为10，需求地个数为10，供应地个数为10，转运时间设置为0.2天，运输时间为2—5天。其他的数据生成情况如下。

①包裹运输时间和可选供应地信息。在带入包裹信息之前，需根据订单信息整理出包裹信息(如表4所示)。为准确计算成本费用和控制运输时间，根据运输费率、运输时间要求的不同近一步细分包裹种类，再对同类包裹进行整合，将出发地和需求地相同的包裹集中打包，到达需求地之后再拆包。

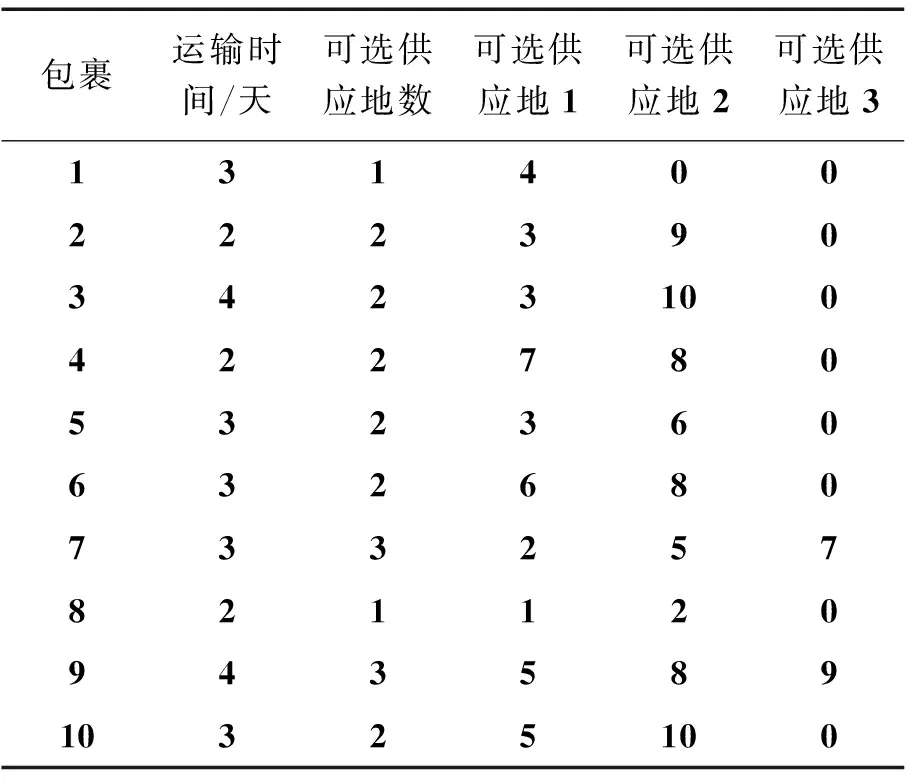
表4　包裹信息

②编号1—3号备选物流中心的固定成本费、包裹分摊管理费、供应地和需求地与物流中心的运输费率和运输时间如表5所示。

固定成本费：包括土地购买租赁成本、基础建设成本、设备购买成本等。为避免固定成本金额太大对算例分析产生决定性影响，所以设置成一样的金额5 000 000元。

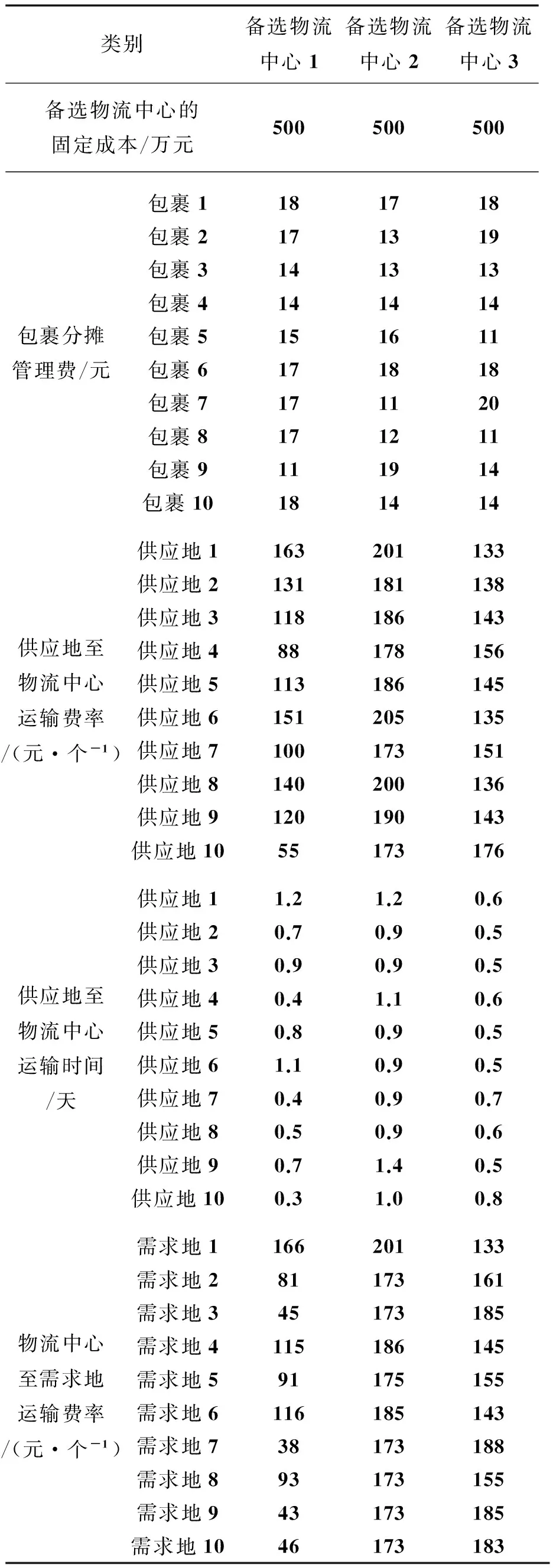
表5　物流中心信息

续表5

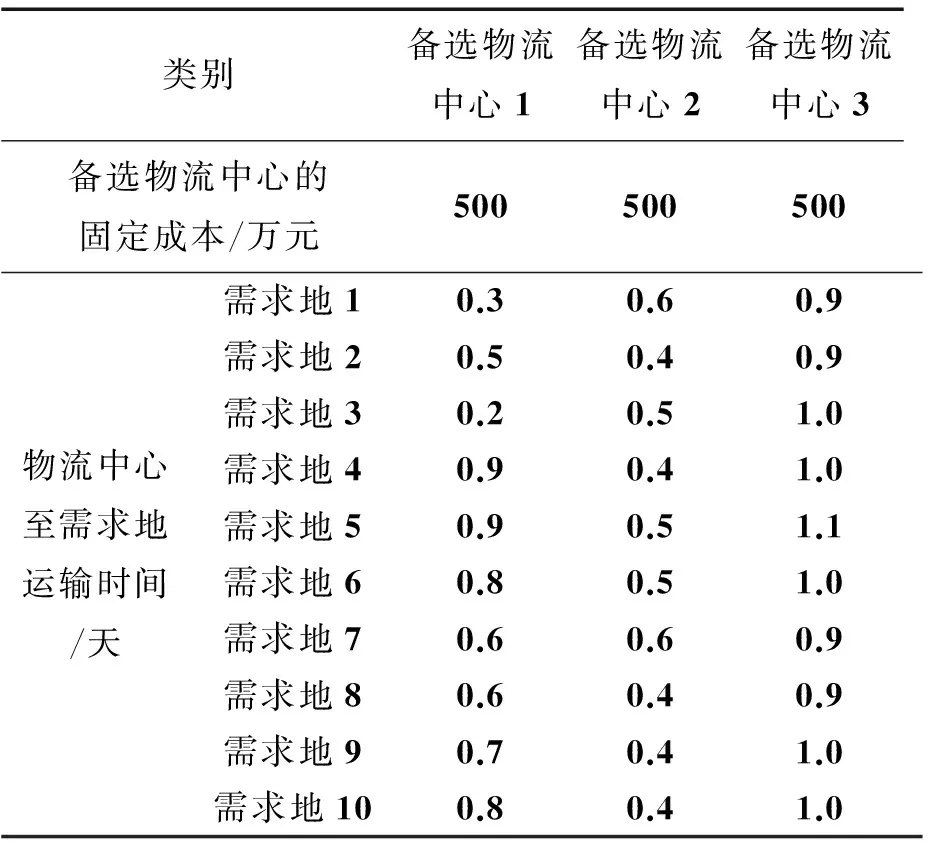
类别备选物流中心1备选物流中心2备选物流中心3备选物流中心的固定成本/万元500500500物流中心至需求地运输时间/天需求地10.30.60.9需求地20.50.40.9需求地30.20.51.0需求地40.90.41.0需求地50.90.51.1需求地60.80.51.0需求地70.60.60.9需求地80.60.40.9需求地90.70.41.0需求地100.80.41.0

包裹分摊管理费：包括包裹包装费用、仓储管理费用等在物流中心发生的费用。

供应地到物流中心运输费率：由包裹重量、体积、运输方式和路线决定。

物流中心到需求地运输费率：由包裹重量、体积、运输方式和路线决定。

③包裹需求量和供应量如表6所示。

3.2选址结果

①通过matlab可得到：当选择备选物流中心1时，最佳适应值为202 332，总费用为519 7668；当选择物流中心2时，最佳适应值为37 483，费用为5 361 079；选择物流中心3时，最佳适应值为93 508，总费用为5 302 514；综合比较后最终选择物流中心1。

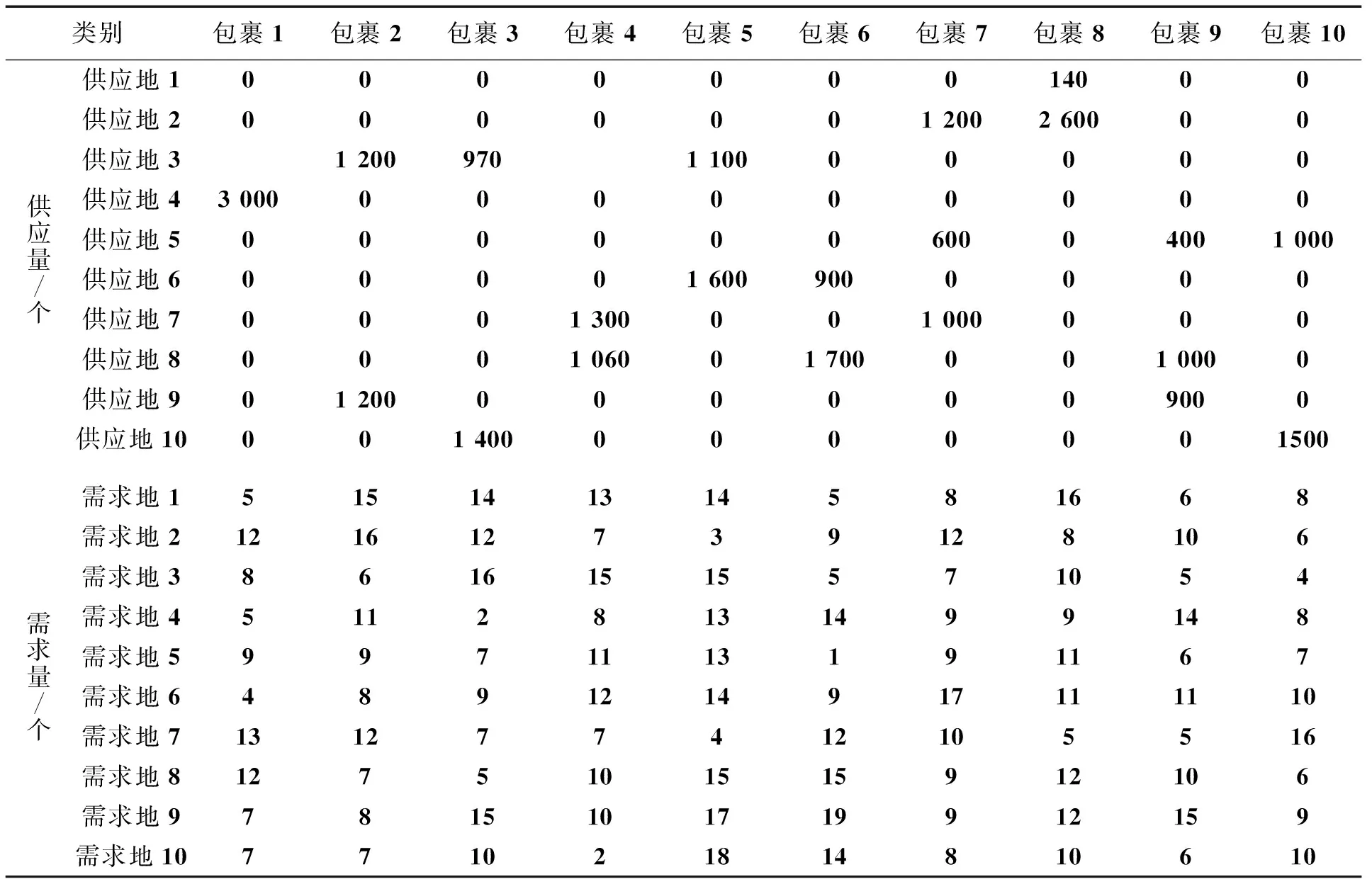
表6　需求量和供应量

②最佳选址方案所对应的最佳运输路线，如图2所示。

第1种包裹的运输路线的字符串“1 1 4 5 1 2 4 12 1 3 4 8 1 4 4 5 1 5 4 9 1 6 4 4 1 7 4 13 1 8 4 12 1 9 4 7 1 10 4 7”表示：第1种包裹：供应地4往需求地1运输5个；供应地4向需求地2运输12个；供应地4向需求地3运输8个；供应地4向需求地4运输5个，供应地4向需求地5运输9个，供应地4向需求地6运输4个，供应地4向需求地7运输13个，供应地4向需求地8运输12个，供应地4向需求地9运输7个，供应地4向需求地10运输7个。

其他种类包裹的运输路线以此类推。

图2　运输路线方案Fig.2　Transport route scheme

③图3表示3个备选物流中心的50代最大适应值和最小适应值的迭代结果。图像显示第1个备选物流中心迭代到约16代的时候开始收敛，第2个备选物流中心迭代到约20代的时候开始收敛，第3个备选物流中心迭代到约36代的时候开始收敛。因此，采用遗传算法具有较好的收敛性。

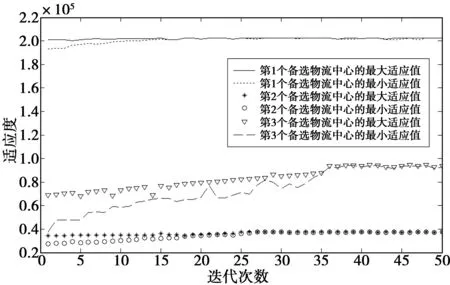
图3　收敛趋势图Fig.3　Convergence trend graph

4结束语

结合电子商务物流中心的特征，利用混合整数规划模型建立了以成本费用最小为目标函数、运输时间和供应需求关系为约束条件的规划模型，再利用遗传算法对模型的求解过程进行了优化改进，在遗传算法编码方案设计时，将问题转化为求解运输路径最优，满足运输时间和需求供应关系；并通过随机生成的数据进行了仿真，验证了模型有效性，得出最优物流中心选址结果、运输路线方案和供应地选择方案。论文为电子商务区域物流中心选址提供了解决方案，具有一定的理论意义和实践意义。

参考文献：

[1]NOZICK L K,TURNQUIST M A. Inventory, transportation, service quality and the location of distribution centers[J]. European Journal of Operational Research,2001(129):362-371.

[2]LIU S,CHAN F T S,CHUNG S H.A study of distribution center location based on the rough sets and Interactive multi-objective fuzzy decision theory[J].Robotics and Computer-Integrated Manufacturing,2011,27(2):426-433.[3]WANG X B,YI Junli. Research on logistics distribution center location model and evaluation under electronic commerce[J].Journal of Systems & Management,2006,1(3):402-406.

[4]秦固.基于蚁群优化的多物流配送中心选址算法[J].系统工程理论与实践,2006(4):120-124.

QIN Gu.Logistics Distribution Center Allocation Based on Ant Colony Optimization[J].Journal of System Engineering Theory and Practice,2006(4):120-124.

[5]吴筱娴,王应明.电子商务环境下物流配送中心选址问题研究[J].物流技术,2015,34(11):90-93.

WU Xiaoxian, WANG Yingming.Study on Location Problem of Logistics Distribution Center under E-commerce Environment[J].Journal of Logistics Technology,2015,34(11):90-93.

[6]张晓楠，范厚明，李剑锋.B2C物流配送网络双目标模糊选址模型与算法[J].系统工程理论与实践,2015(5):1202-1213.

ZHANG Xiaonan,FAN Houming,LI Jianfeng.Bi-objective fuzzy location model and algorithm for the design of logistics distribution network in B2C e-commerce[J].Journal of System Engineering Theory and Practice,2015(5):1202-1213.

[7]关菲，张强.模糊多目标物流配送中心选址模型及其求解算法[J].中国管理科学,2013(S1)：57-62.

GUAN Fei,ZHANG Qian.A Fuzzy Multi-Objective Logistics Distribution Center Location Model and Its Solution Algorithm[J], Chinese Journal of Management Science, 2013(S1): 57-62.

[8]过晓芳,王宇平.考虑物流服务水平的物流配送规划多目标模型[J].西南交通大学学报, 2012, 47(5): 874-880.

GUO Xiaofang,WANG Yuping.Multi-objective Model for Logistics Distribution Programming Considering Logistics Service Level[J].Journal of Southwest Jiao Tong University, 2012, 47(5):874-880.

[9]胡琳.基于改进粒子群优化算法的物流配送中心选址技术[J].统计与决策,2011(4): 57-59.

HU Lin.Logistics distribution center location technology based on Improved Particle Swarm Optimization Algorithm[J].Journal of Statistics and Decision,2011(4):57-59.

[10] 胡大伟,陈诚.遗传算法(GA)和禁忌搜索算法(TS)在配送中心选址和路线问题中的应用[J].系统工程理论与实践,2007(9):171-176.

HU Dawei, CHEN Cheng.Application of GA and TS in Logistics Distribution Center Location and Routing Problem[J].Journal of System Engineering Theory and Practice,2007(9):171-176.

DOI：10.3979/j.issn.1673-825X.2016.04.022

收稿日期：2016-03-23

修订日期：2016-05-04通讯作者：周昔敏1601485148@qq.com

基金项目：重庆市社会科学规划培育项目(2015py33)；重庆市教育委员会科学技术研究项目(KJ1400415)。

Foundation Items：The Social Science Training Project of Chongqing Municipal, P.R. China(2015py33);The Science and Technology Research Project of Chongqing Municipal Education Commission, P.R. China(KJ1400415)

中图分类号：TP29;F570.5

文献标志码：A

文章编号：1673-825X(2016)04-0593-08

作者简介：

邓学平(1979-)，男，四川省南充市人，副教授，博士，主要研究方向为供应链与现代物流工程。E-mail：dengxp@cqupt.edu.cn。

周昔敏(1991-)，女，四川省南充市人，硕士研究生，主要研究方向为现代物流工程(物流运作与管理)。E-mail：1601485148@qq.com。

田帅辉(1984-)，男，河北省邯郸市人，副教授，博士，主要研究方向为现代物流与供应链管理。E-mail：tiansh@cqupt.edu.cn。

(编辑：张诚)

Research on integrated optimization of location and routing for B2C E-commerce logistics center

DENG Xueping，ZHOU Ximin，TIAN Shuaihui

(School of Economics and Management，Chongqing University of Posts and Telecommunications, Chongqing, 400065, P.R.China)

Abstract:For the purpose of optimizing the B2C E-commerce logistics system, combining with the characteristics of B2C e-commerce, a mixed integer programming model, which takes the minimum logistics cost as the objective function, and with transport time and the supply-demand relationship as the constraint conditions, is constructed. The mixed integer programming model of E- commerce logistics center location has been changed into solving optimal transport path problem by improved genetic algorithm, and the penalty operator has been set for more than transportation time restrictions, appropriate chromosome encoding, crossover operator, mutation operator, penalty function are also designed. Finally, an example has been simulated using randomly generated data and by Matlab software, which proves the effectiveness of the model.

Keywords：logistics location; routing optimization; mixed integer programming; genetic algorithm; e-commerce