非合作直扩信号伪码及信息序列联合盲估计

强幸子，张天骐，赵军桃，王俊霞

(重庆邮电大学 信号与信息处理重庆市重点实验室，重庆 400065)



非合作直扩信号伪码及信息序列联合盲估计

强幸子，张天骐，赵军桃，王俊霞

(重庆邮电大学 信号与信息处理重庆市重点实验室，重庆 400065)

摘要：研究了短码直接序列扩频信号扩频序列及信息序列联合盲估计问题。在已知码片速率和扩频码周期的前提下，对接收信号以2倍伪码周期进行分段构造信号矩阵，然后对其进行奇异值分解，对最大和次大左奇异向量进行线性变换，得到信息序列；利用自相关函数从最大和次大右奇异向量中得到扩频码序列。该算法在失步时间未知的情况下能够同时估计出伪码序列及信息码序列，避免了传统特征值分解盲估计算法利用2个矢量空间组合扩频序列时存在的相位模糊问题。同时，在引入了矩阵的线性变换后，避免了不同时延估计结果存在模糊的问题，提高了盲估计性能。通过理论分析和计算机仿真结果表明：该算法能够有效估计扩频序列，并且具有精确度高、性能不受时延大小影响等优点。

关键词：直接序列扩频信号；伪码序列 ；信息序列；奇异值分解

0引言

直接序列扩频信号由于其抗干扰能力强，保密性能好等优点，在军事和民用通信系统中得到广泛应用。

在非协作通信系统中，为了对传输信息进行有效恢复，通常需要对扩频序列进行估计，以达到盲解扩的目的。文献[1-4]利用特征值分解的方法对伪码序列进行估计，该方法在同步时，能够准确地估计出伪码序列；在异步时，存在失步时间估计不准和难以解决分段伪码序列拼接时相位模糊的问题。文献[5]采用2倍伪码周期为窗口进行奇异值分解的方法对信息序列和伪码序列进行估计。该方法在异步时能够对信息序列和伪码序列实现准确估计；在同步或失步时间较小时，该方法进行奇异值分解得到2个大小相等或相近的最大和次大奇异值，此时最大和次大奇异向量存在模糊关系，不能准确估计出信息序列和伪码序列。

针对文献[5]在同步时估计信息序列和伪码序列存在的问题，本文利用最大和次大奇异向量之间的线性关系对其进行线性变换，能够有效抑制失步时间较小或较大时存在的模糊。

1信号模型

非协作通信接收端得到的短码DS-SS信号为

(1)

(1)式中

(2)

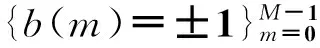
假设信号伪码周期和码片宽度[5-6]已知， (1)式进行码速率采样后，可得离散时间信号模型为

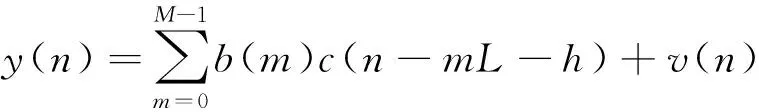
(3)

(3)式中，h∈[0,L)为传输时延对应的离散采样值。

将采样序列按照向量2Nc×1进行分段为

(4)

(4)式中：

cr(h)=[c(h),…,c(Nc-1),0,…,0]T；

c=[0,…,0,c(0),…,c(Nc-1),0,…,0]T；

cl(h)=[0,…,0,c(0),…,c(h-1)]T

(5)

假设接收到M+1个信息码序列，可以得到M个x(n)[9]有

X=[x(1),…,x(M)]=

[cr(h)b(0)+cb(1)+cl(h)b(2)+v(1),…,

cr(h)b(M-1)+cb(M)+cl(h)b(M+1)+

v(M)]=cr(h)b0+cb1+cl(h)b2+v

(6)

(6)式中：b0=[b0,b1,…bM-1]；b1=[b1,b2,…bM] ；b2=[b2,b2,…bM+1] 。

2信息序列盲估计

因为b(m)服从等概率随机分布，并且取值为±1，故有

(7)

结合(8)式计算接收信号协方差有

R1=E{XHX}=

E{[b0cr+b1c+b2cl+n]H·

[crb0+cb1+clb2+n]}=

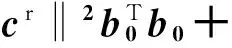
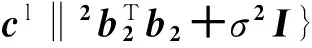
(8)

由矩阵论知识易知R1特征值和特征向量对应关系如表1

表1　R1特征值和特征向量对应关系

因为信息码序列和扩频码序列的取值均为±1。故表1中‖b1‖2=‖b0‖2=‖b2‖2=M，‖c‖2=L，‖cr‖2=L-h，‖cl‖2=h。

当传输时延h在「L/2」附近时，λ1=ML+σ2，是协方差矩阵R1对应的最大特征值。此时，λ1对应的全部特征向量为：kb1(k≠0)，故当对X进行奇异值分解时，总有最大奇异值对应的左奇异向量是kb1(k≠0)；当h不在「L/2」附近时，即h较小、较大或为0时，这里假设h较小或为0不失一般性。此时，最大特征值仍为λ1=ML+σ2，第2大特征值为λ2=M(L-h)+σ2，并且由于h较小或为0，从而λ1与λ2的值近似相等。与此同时，b1和b0仍然是协方差矩阵R1的特征向量，但协方差矩阵R1的最大特征值λ1和λ2(λ2与λ1近似相等)所对应的特征向量是b1和b0所构成信号子空间的线性变化，故此时对X进行奇异值分解时，最大的2个奇异值对应的左奇异向量实际上是b1和b0所构成信号子空间的线性变化，而并非信号子空间。因此，当h不在「L/2」附近时，对X进行奇异值分解所得到的信号子空间存在相干模糊。

这里利用估计得到的信号子空间与真实信息序列有相同的基础解系，可对存在模糊的信息子空间做矩阵变换估计出真实信息序列。

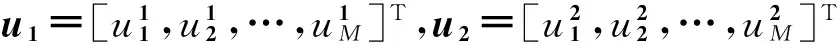
(9)

利用b0,b1,b2之间的重叠关系，总有

(10)

(10)式中

(11)

即

Uxq=0

(12)

(12)式中

(13)

由此我们可以得到q

(14)

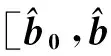
本文对奇异值分解后的信号子空间进行线性变换得到信息序列的估计。当延时h较小或者较大时，最大特征值和次大特征值的大小较为接近，此时得出的信号子空间与真实信号向量之间仍然存在着这种线性变换的模糊关系，故这种方法仍然有效。当T0取在整个伪码序列周期Tc的中间位置时，最大和次大奇异值所对应向量的这种相干关系减弱。

算法步骤为

1)对XT奇异值分解，得到右奇异向量u1,u2和3个较大奇异值λ1,λ2,λ3。

2)判断λ1-λ2和λ2-λ3之间的大小关系：

若前者比后者大，则直接输出sign(u1)作为b1的估计；

若后者比前者大，首先通过(15)式所示的互相关函数判断h范围。

(15)

如果n=1时，则h<「L/2」，否则，h≥「L/2」；

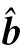
3伪码序列盲估计

根据奇异值分解定理，矩阵XT可分解为XT=UΔVH,其中U,V为酉矩阵，Δ为奇异值所构成的对角阵。

根据矩阵分解性质可知，XT的奇异值和左奇异向量为R2=E{XXH}的特征值和特征向量。由文献[5]推导可知，R2特征值和特征向量对应关系如表2所示。当传输时延h在「L/2」附近时，利用文献[5]的方法能够准确地估计出伪码序列c；当传输时延h不在「L/2」附近时，最大和次大左奇异向量也存在干扰模糊。

表2　R2特征值与特征向量对应关系

这里结合信息序列估计中对h范围判定，再采用最大谱范数法对h进行精确估计。

最大谱范数的定义为

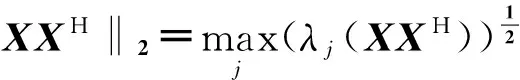
(16)

(16)式中，λj(XXH)表示矩阵XXH的第j个特征值。该方法估计延时原理为连续改变分段起始点的位置m，m=0,1,…,L-1，当分段起始点位置为m=h时，‖R2‖2取得最大值。这里利用信息序列估计中对h范围的判定，可以有效减小最大谱范数法估计延时的运算量。

算法步骤：

1)对XT做奇异值分解，右奇异向量为v1,v2；

2)根据第3部分算法步骤2判断结果：

若前者比后者大，则直接对v1利用(17)式进行时延估计

(17)

若前者比后者小，则根据步骤2对h判断结果进行分类

当h<「L/2」，则在h∈[0,「L/2」)利用最大谱范数法对时延进行估计；

当h≥「L/2」，则在h∈ [「L/2」,L)利用最大谱范数法对时延进行估计。

3)利用估计出的时延在v1中获取伪码序列。

4计算机仿真结果及分析

实验1伪码、信息序列联合盲估计仿真。

仿真信号采用BPSK调制，信噪比为-12 dB，采用127 bit的m序列作为伪码，信号长度为101个伪码周期，形成100个时间窗。每个伪码周期采样127 bit。

假设失步时间5 bit，盲估计序列与实际序列符号全部相同如图1，因此本文方法能够实现最大与次大右奇异向量消模糊。同时，本文方法估计伪码序列效果如图2所示。

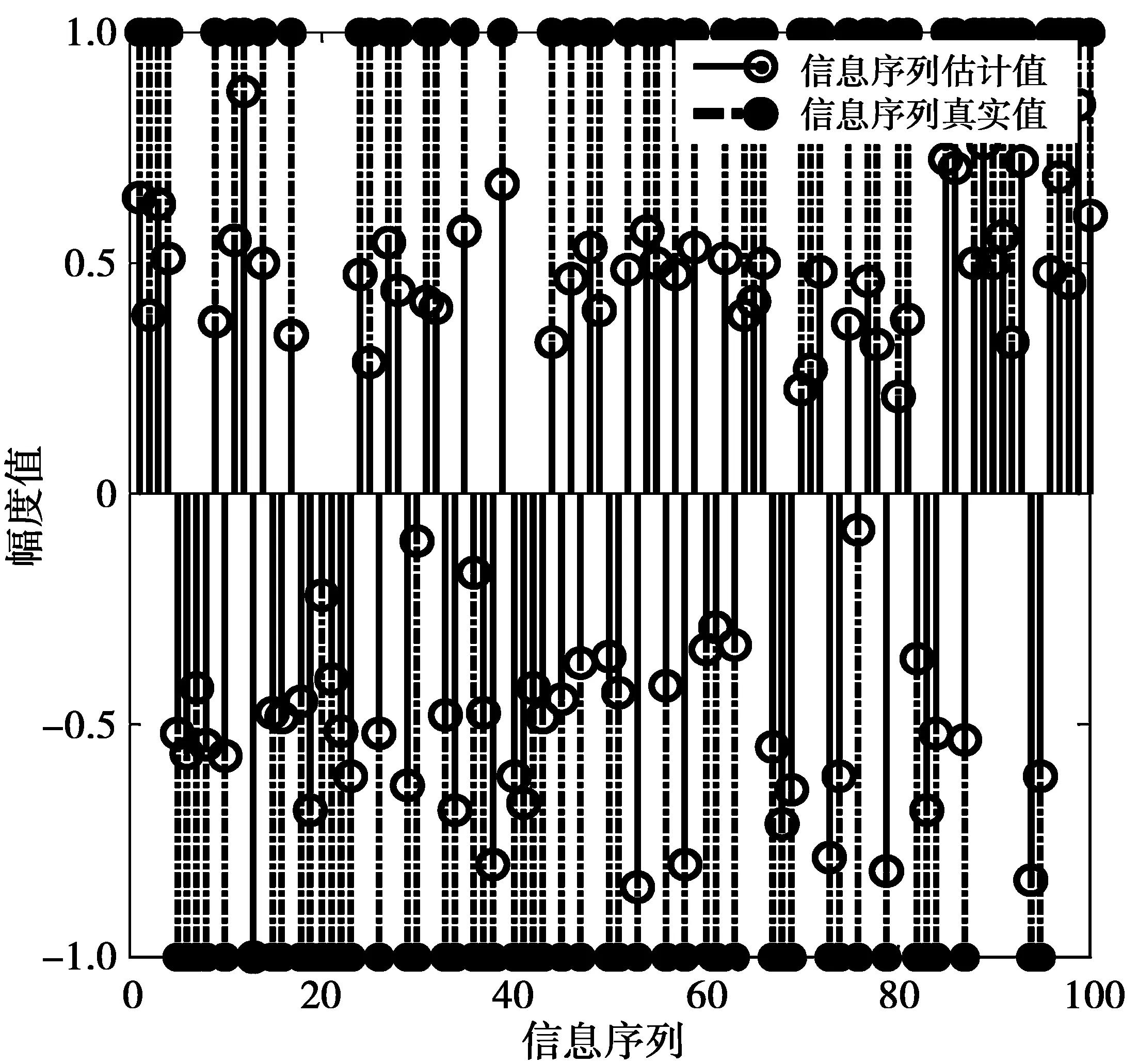
图1　信息序列估计值与真实值比较Fig.1　Information sequence estimation compared with the real value

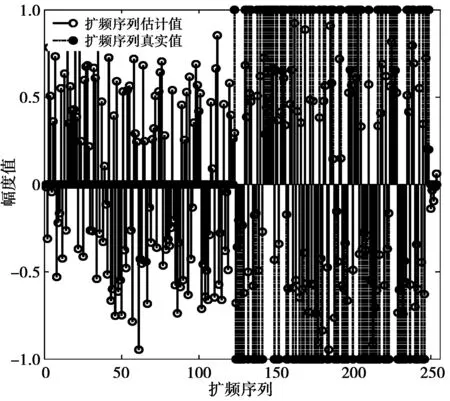
图2　伪码序列估计值与真实值比较Fig.2　PN code estimation compared with the real value

实验2信息序列盲估计性能分析。

仿真分别对文献[5]和本文算法在SNR为-20 dB—0 dB时信息序列估计的正确率进行对比,对每个SNR值蒙特卡洛仿真200次，其他参数如上所述，得到信息序列盲估计正确率性能曲线如图3。由图3可知，本算法在不同信噪比[8]情况下性能均优于文献[5]算法。

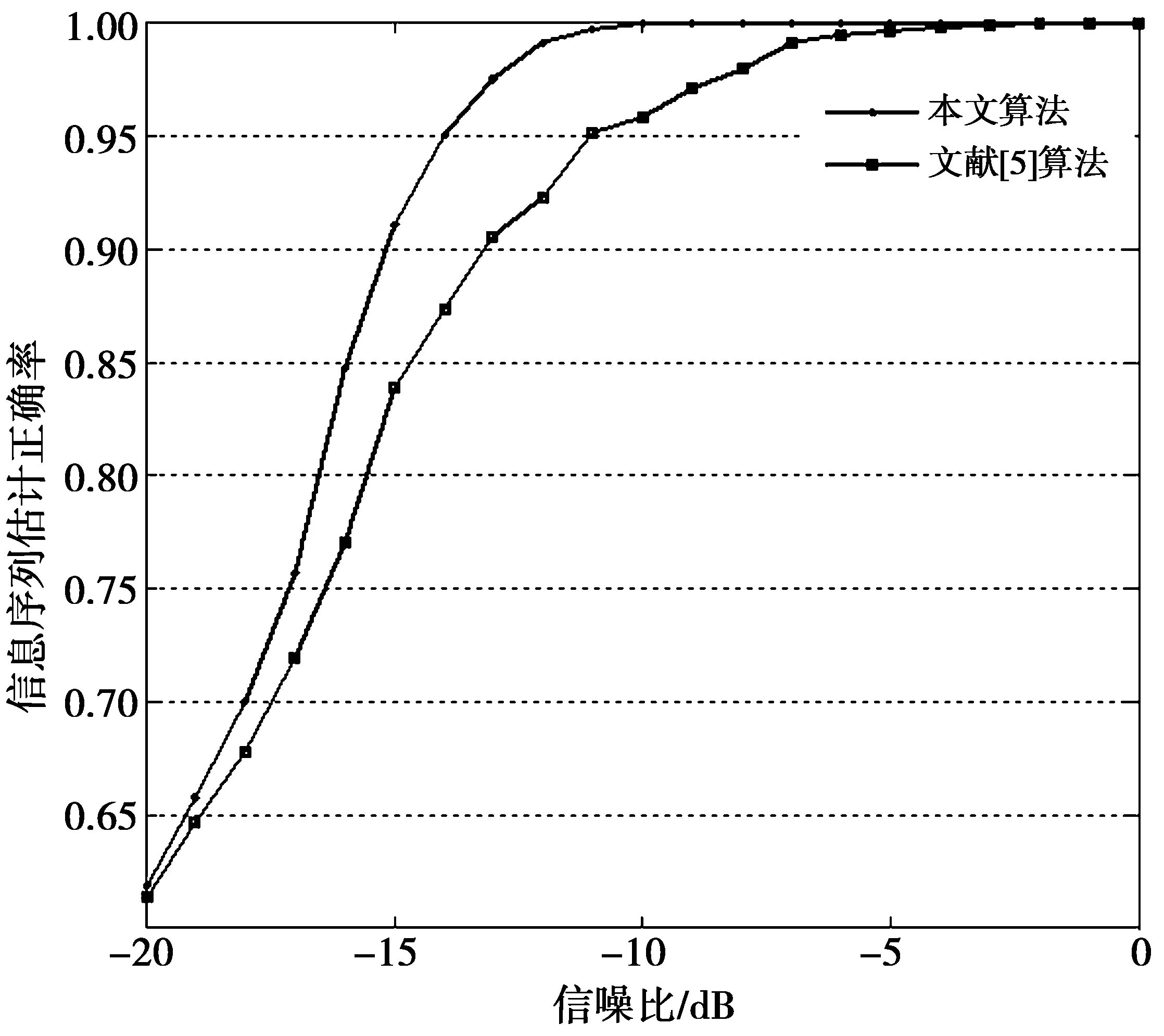
图3　信息序列性能分析Fig.3　performance analysis for Information sequence

实验3伪码序列盲估计性能分析。

仿真在SNR分别为-5 dB，-10 dB，-15 dB，数据组数为5—400时，其他参数不变得到伪码序列盲估计误码率性能曲线如图4。由图4可知，当信噪比固定时，数据组数越多，本文算法对伪码序列估计性能越好。同时，信噪比越大，曲线收敛速度越快，说明当数据组数相同的情况下，信噪比越高，伪码序列估计性能越好。

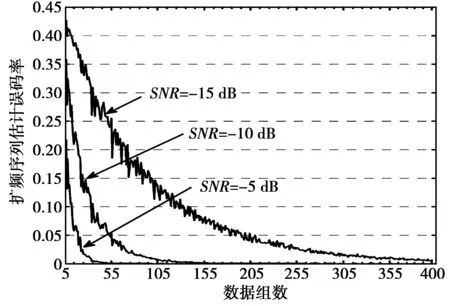
图4　伪码序列性能分析Fig.4　Performance analysis for PN code

5结论

本文将信号以两倍伪码周期长度进行分段，然后通过奇异值分解，分别利用左奇异向量和右奇异向量得到信息序列和伪码序列估计值。同时，针对失步时间较小或较大而产生的模糊问题，利用矩阵线性变换对左奇异向量消模糊，并利用自相关函数对右奇异向量消模糊。仿真结果表明该算法具有抗干扰能力强且性能稳定等优点。在整个算法推导和仿真实验中，该文只考虑了加性高斯白噪声，但在实际信号中，还存在多径、窄带等干扰，针对多种形式的干扰还有待进一步研究。

参考文献：

[1]BUREL G, BOUDER C. Blind estimation of the pseudo-random sequence of a direct sequence spectrum signal[C]∥MILCOM 2000. 21 st Century Military Communications Conference Proceedings. Los Angeles California USA:[s.n.], 2000: 967-970.

[2]陆俊，路思羽,韩方景，等.侦察中的直扩信号PN序列盲估计算法[J].无线电工程,2011,41(8):15-17.

LU Jun, LU Siyu, HAN Fangjing, et al. Blind estimation algorithm for PN sequence of direct sequence spread spectrum signals in communication reconnaissance[J]. Radio Engineering of China , 2011, 41(8): 15-17.

[3]ZHANG T Q, MU A P, ZHANG M C. Analyze the eigen-structure of DS-SS signals under narrow band interferences[J]. Digital Signal Processing, 2006, 16(6): 746-753.

[4]ZHANG T Q, MU A P. A modified eigen-structure analyzer to lower SNR DS-SS signals under narrow band interferences[J]. Digital Signal Processing, 2008,18(4): 526-529.

[5]任啸天，徐晖，黄知涛，等. 短码 DS-SS 信号扩频序列及信息序列联合盲估计方法[J].通信学报，2012, 33(4): 169-175.

REN Xiaotian, XU Hui, HUANG Zhitao, et al.. Joint blind estimation of the spread-spectrum sequence and information sequence for short-code DS-SS signal[J]. Journal on Communications, 2012, 33(4): 169-175.

[6]YAO Y W, VINCENT H. Bind detection of synchronous CDMA in on-Gaussian channels[J]. IEEE Transactions on Signal Processing, 2004, 52(1): 271- 279.

[7]QIU P Y, HUANG Z T, JIANG W L, et al. Blind classification of the short-code and the long-code direct sequence spread spectrum signals[J]. IET Signal Processing, 2010, 4(1): 78-88.

[8]刘源源，江雪，谢显中，等.一种改进的BPSK信噪比估计方法及其FPGA实现[J].重庆邮电大学学报，2014,26(5):630-635.

LIU Yuanyuan, JIANG Xue, XIE Xianzhong, et al. An improve SNR estimation for BPSK signals and its FPGA implementation[J].Journal of Chongqing University of Posts and Telecommunications, 2014, 26(5): 630-635

[9]TOMMI K, KOIVUNEN.V Blind dispreading of short-code DS-CDMA signals in asynchronous multi-user systems[J]. Signal Processing, 2007, 87: 2560-2568.

DOI：10.3979/j.issn.1673-825X.2016.04.005

收稿日期：2015-08-05

修订日期：2016-06-15通讯作者：强幸子qiangxingzi@163.com

基金项目：国家自然科学基金项目(61371164)；重庆市杰出青年基金项目(CSTC2011jjjq40002)；重庆市自然科学基金项目(CSTC2012JJA40008)；重庆市教育委员会科研项目(KJ130524)

Foundation Items：The National Natural Science Foundation of China (61371164); The Chongqing Distinguished Youth Foundation (CSTC2011jjjq40002); The Natural Science Foundation of Chongqing (CSTC2012JJA40008); The Research Project of Chongqing Educational Commission(KJ130524)

中图分类号：TN914.53

文献标志码：A

文章编号：1673-825X(2016)04-0468-05

作者简介：

强幸子(1986-)，男，陕西乾县人，硕士研究生，主要研究方向为直扩信号盲处理。E-mail：qiangxingzi@163.com。

张天骐(1971-)，男，四川眉山人，教授，博士，主要研究方向为语音信号处理，通信信号的调制与解调、盲处理、神经网络实现等。E-mail: zhangtq@cqupt.edu.cn

赵军桃(1990-)，男，山西吕梁人，硕士研究生。主要研究方向为通信信号处理。E-mail: 1012928803@qq.com

(编辑：张诚)

Blind estimation of non-cooperative direct sequence spread spectrum signals and information sequence

QIANG Xingzi, ZHANG Tianqi, ZHAO Juntao, WANG Junxia

(Chongqing Key Laboratory of Signal and Information Processing, Chongqing University of Posts and Telecommunications，Chongqing 400065，P.R.China)

Abstract:Blinding estimation combined spread-spectrum sequence with information sequence of DS-SS signals is studied. The chip rate of the Pseudo-Noise (PN) sequence and the PN sequence period need to be uncovered. Firstly, received signal is sectioned with double pseudo-code cycle to construct the signal matrix, upon which singular value decomposition (SVD) is applied. Then information sequence is obtained by linear transformation of largest and secondary largest left singular vectors , PN sequence is worked out from largest right singular vector with the utilization of autocorrelation function. Without the knowledge of desynchronization time, the proposed method is able to estimate both the spread-spectrum sequence and information sequence blindly. Meanwhile，it avoids solving the problem of the phase ambiguity when useing two vectors to reconstruct spread-spectrum sequence, which is based on EVD blinding estimate algorithm. Furthermore, the ambiguity at different desynchronization time is avoided by using linear transformation of matrix. The theoretical analysis and simulations show that, the proposed method can estimate PN sequence and information sequence effectively, and it has higher estimation accuracy and is not affected by the level of time delay.

Keywords：direct sequence spread spectrum (DSSS) signal; pseudo noise sequence; information sequences; singular value decomposition