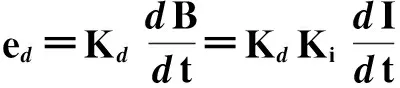电磁流量计矩形波励磁的信号模型研究

李新伟，李　斌，张　欣，王高扬，王贯兵

(上海大学 机电工程与自动化学院，上海 200072)



电磁流量计矩形波励磁的信号模型研究

李新伟，李斌，张欣，王高扬，王贯兵

(上海大学 机电工程与自动化学院，上海 200072)

摘要：由于传统矩形波励磁模型未兼顾传感器磁路系统和励磁系统的影响，忽略了信号采样过程，因而无法建立符合实际的矩型波励磁流量信号模型。基于励磁电流的一般方程，提出了一种矩形波励磁模型，该模型建立了磁感应强度与磁路系统、励磁系统的数学关系，进而量化了微分干扰和同相干扰。在该励磁模型基础上，模拟电磁流量计对实际信号的采样过程，进一步提出了矩形波励磁的流量信号模型，并给出了模型参数的辨识方法。从流量信号仿真、模型基本参数辩识、零点漂移预测及基本误差估计4方面进行模型验证。仿真与实验结果表明，在DN50传感器上，其零点漂移预测的最大误差为1.48 mm/s，基本误差估计的最大偏差为0.270%。

关键词：电磁流量计；信号模型；矩形波励磁；零点漂移；基本误差

0前言

电磁流量计是基于法拉第电磁感应定律的流量仪表，其测量方程[1]建立在磁场稳定条件下。它具有高精度、高稳定性、无节流阻流部件、不易堵塞及耐腐蚀性等特点，所以，在化工、石油、冶金、造纸等行业得到广泛的应用。作为工业在线检测仪表的电磁流量计，首先要考虑它的稳定性，主要是零点稳定性[2]。为确保具有较好的零点稳定性，励磁频率一般会定在较低频率上。由于低频矩形波励磁能够兼顾直流励磁和交流励磁两者的优点，是主流的励磁方式。随着电磁流量计在液固两相流(如泥浆、纸浆)等场合的运用，高频励磁或双频励磁能有效降低浆液噪声的影响[3-4]，进而提高测量精度，被广泛应用于实际生产中。但励磁频率的提高会破坏零点的稳定性，对仪表的性能产生不利影响。在实际应用环境中进行相关性能测试实验效率低, 而且成本高，因此，有必要建立一种能够反映实际性能的矩形波励磁的流量信号模型，从而推动电磁流量计的研究探索。表1为主要符号对照表。

表1　主要符号对照表

1相关研究

当前国内外已有专家学者在流量信号模型方面做了一些研究。文献[5]从理论上分析了正弦波励磁中磁通变化引起的零点稳定性问题，基于“变压器效应”和涡电流影响，提出了一种零点预测模型。文献[6]提出了一种基于实验数据的2个阶段拟合方法，建立了交流励磁的信号模型，该模型能够描述励磁信号、流量与传感器输出的关系。文献[7]基于微分干扰等实现了对交流励磁的流量信号建模。在对矩形波励磁的流量信号模型研究中，文献[8]指出了高频矩形波励磁产生的尖峰噪声会引起零点不稳定，提出了一种零点漂移修正的方法，能够提高零点和测量的稳定性，但论文并未对矩形波励磁的信号模型进行研究。文献[9]利用有限元方法建立了矩形波励磁的传感器励磁模型, 进一步求解感应电势信号, 能够模拟流量信号的动态性能，但该模型建立在理想电流源的条件上，且未考虑信号采样、励磁系统参数影响，不能用于零点漂移预测及基本误差估计，因此，难于运用于实际。文献[10]对明渠电磁流量计的脉冲励磁的信号模型进行了研究。在此基础上，文献[11]建立了脉冲励磁的数学模型，进而对流量信号模型进行了研究，基于励磁电流方程和“变压器效应”，实现了流速的准确估测，但该模型基于脉冲励磁方式，未考虑信号采样的影响，无法对励磁频率等参数的影响展开研究。

通过对现有文献进行分析和总结，目前的信号模型研究中主要存在2个问题:①主要针对交流励磁或脉冲励磁方式，并不适用于主流的矩形波励磁方式，并忽略了实际信号采样的影响;②在对矩形波励磁模型的研究中，目前大多从磁感应强度出发，未引入传感器磁路参数和励磁系统参数的影响。而在实际中，电磁流量计性能与此紧密相关。

在本文中，首先针对矩形波励磁模型，从励磁电流一般方程着手，引入了传感器磁路参数和励磁系统参数，再根据磁感应强度与励磁电流的关系，建立了磁感应强度与传感器磁路、励磁系统参数的数学关系。考虑到微分干扰、同相干扰由磁通变化引起，进而将其量化，从而建立了矩形波励磁的数学模型。其次，在流量信号建模中，针对实际信号采样的影响，本文基于励磁电流方程，得到了流量信号的基本方程，再模拟电磁流量计信号采样过程，最终建立了矩形波励磁的信号模型。相对传统模型，该模型综合了传感器磁路、励磁系统、信号采样的影响，从而更符合实际。文中给出了模型参数辨识的方法，并在流量信号波形仿真、模型参数辨识、零点漂移预测及基本误差估计方面进行了实验。实验结果表明，该模型有效。

2矩形波励磁模型

2.1问题分析

电磁流量计的测量方程是建立在磁感应强度稳定的条件上。磁感应强度的稳定主要体现如下。

1)励磁线圈通电后引起的“变压器效应”和金属部件内感应产生的涡电流会引起微分干扰、同相干扰，影响零点和流量信号，且与传感器线圈、磁芯及电极、金属管等金属部件紧密相关[12]。由于交流励磁会产生较强的微分干扰和同相干扰，且微分干扰比流量信号滞后90°，同相干扰与流量信号同相。采用正交解调方法, 可将流量信息从混有正交干扰的传感器信号中提取出来，再对涡电流相位建模[13]，从而能够建立交流励磁的信号模型。但矩形波励磁中产生的微分干扰、同相干扰与流量信号相位无直接关系，因此，难以对流量信号建模。

2)励磁频率越高，励磁电路恒流模块输出的励磁电流难以保持平稳，导致磁感应强度未进入稳态，与励磁频率、信号采样时序、励磁电流方程有关。因此，传统测量方程中的流量感应电势与流速之间的正比关系不再满足。

2.2数学模型

以三值矩形波励磁方式为目标，本文研究了矩形波励磁的数学模型。三值矩形波励磁等效电路如图1所示。其中，Rx是传感器励磁线圈铜损电阻；Rc是线圈铁损电阻；Lx是线圈等效电感。由于铜损电阻Rx在数值上远小于铁损电阻Rc，忽略铁损电流，并假设磁感应强度取决于励磁电流。

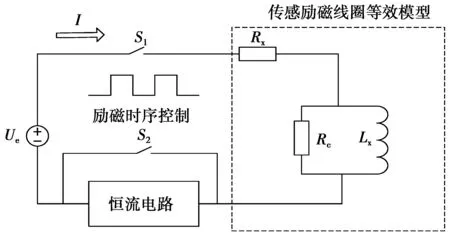
图1　矩形波励磁等效电路Fig.1　Equivalent circuit of rectangular wave excitation

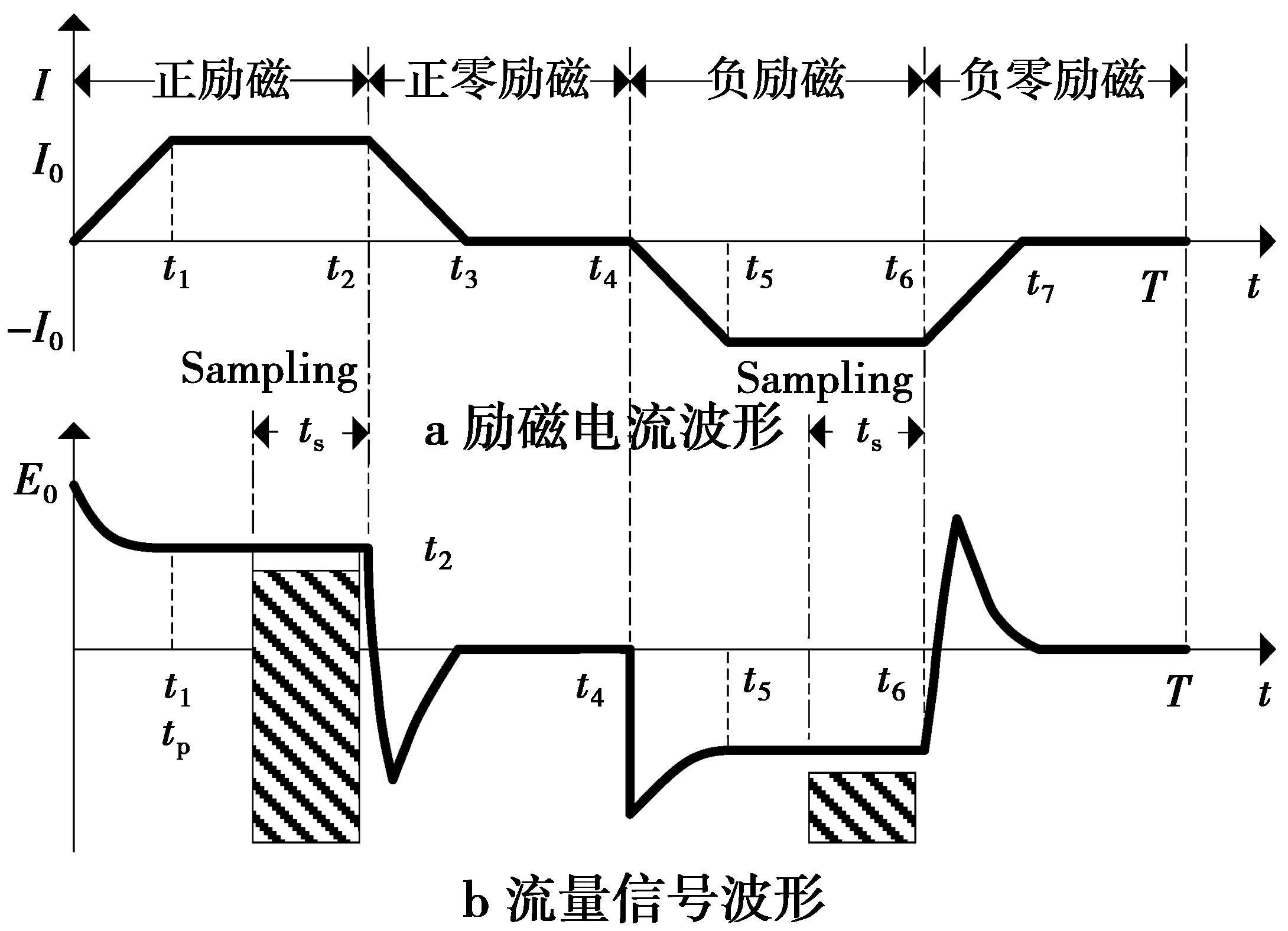
图2a为一个励磁周期T的励磁电流波形；图2b为理论的流量信号波形(流体感应电势)，两者是同步的。其中，ts为采样时间(阴影部分为采样区间)；I0为稳态励磁电流；E0为传感器输出的流量信号。

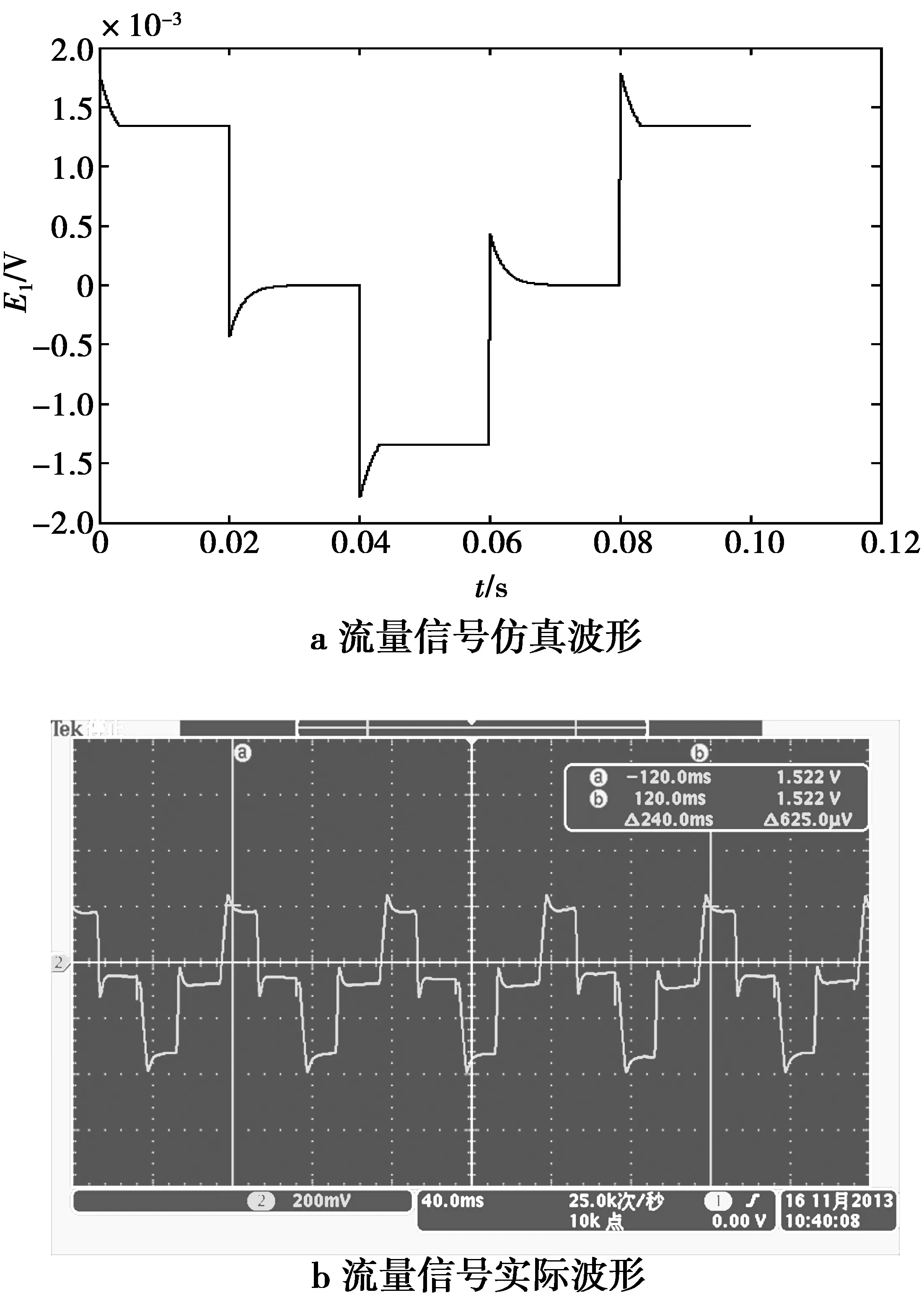
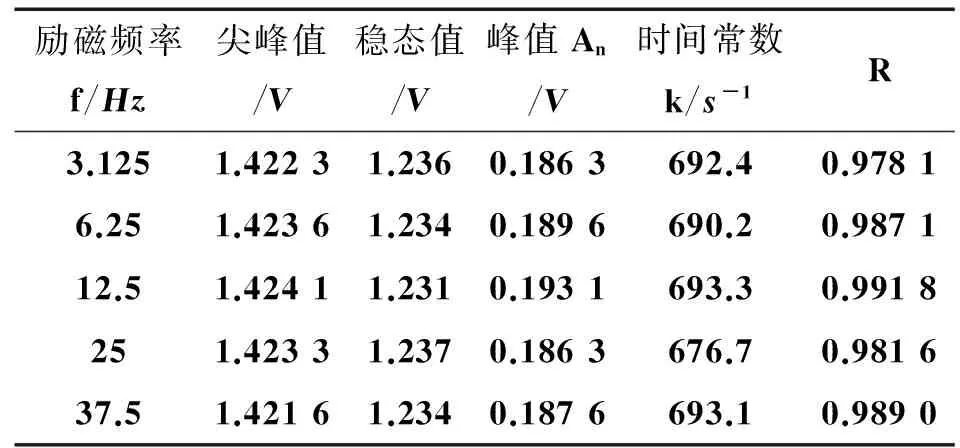
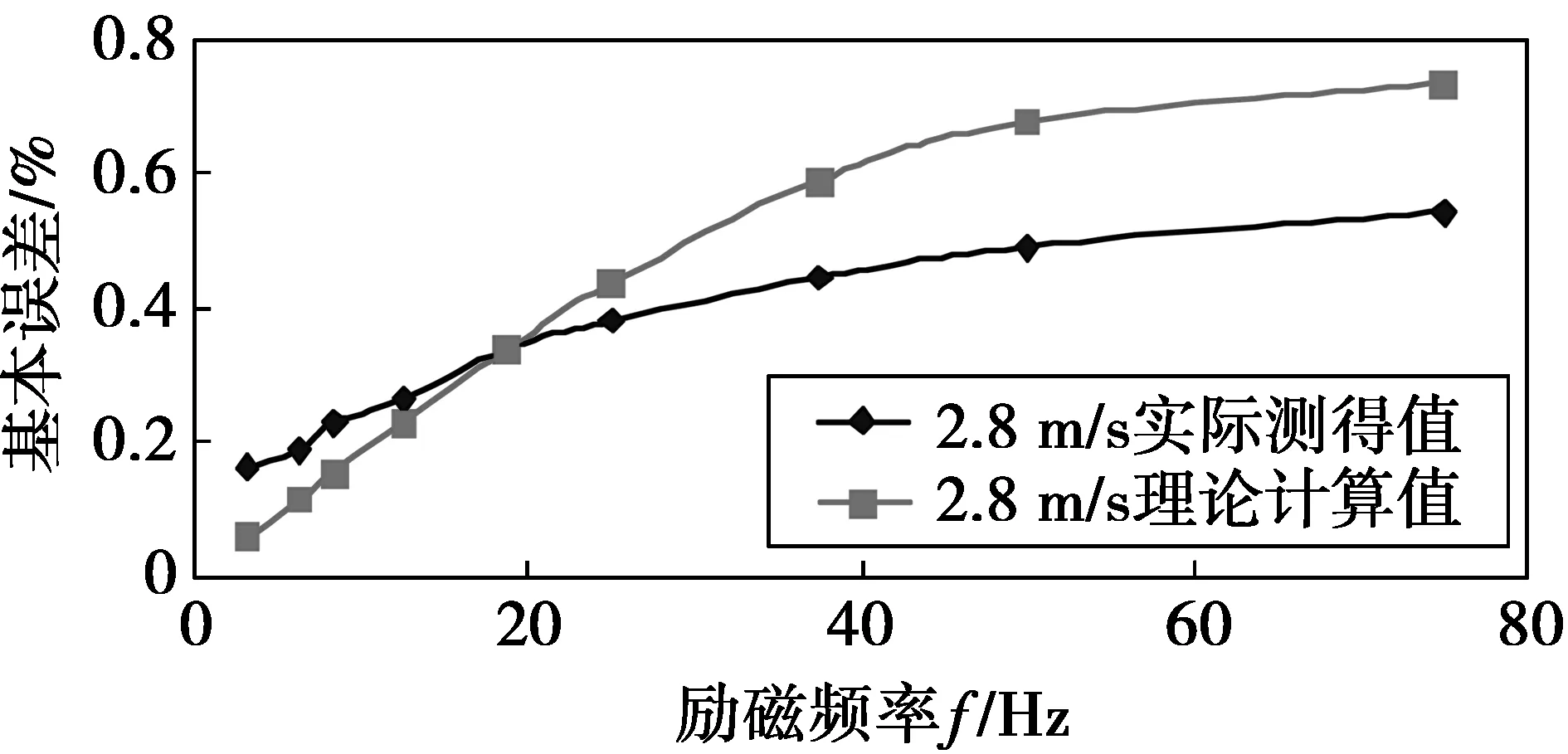
正励磁(0

图2　励磁电流和流量信号的示意图Fig.2　Schematic of excitation current and flow signal

(1)显然，励磁电流方程与传感器磁路、励磁系统有关。I进入稳态的调节时间tp为

(2)由于传感器等效电感Lx的存在，励磁电流会存在上升的渐变过程，导致磁感应强度B也处在不稳定的状态，具体表现为微分干扰、同相干扰，在流量信号波形上形成尖峰噪声(见图2b)，从而会影响零点的稳定性和流速的测量。

(3)(3)式中：Kd，Kt分别表示微分干扰和同相干扰的强度，与传感器磁路、励磁系统有关。此外，正零励磁时(t2

3矩形波信号模型

3.1基本模型

设转换器对流量信号的放大倍数为Kv，并忽略工频干扰、电压噪声、极间噪声。根据矩形波励磁模型，正励磁(0

E1(t)=Kv(BDν+ed+eT)=

(4)

在电磁流量计实际信号采样中，正、负励磁的采样时间均为ts，为降低尖峰噪声影响，一般在正、负励磁信号的后半部分采样，如图2b所示，正励磁的采样结束点tsed=T/4，起始点tsst=tsed-ts。取采样时间ts=T/8，即正、负励磁的信号采样时间为正、负励磁时间的一半，以保持相同的信噪比。再对E1在[tssttsed]定积分，得到流量信号采样值E1s为

当0

(5)当T/8≤tp

(6)(6)式进一步化简为

(7)将(7)式作为流量信号的一般方程。各个励磁频率的信号采样时间不同，需将各励磁频率的E1s归一化到统一时间标度t*。由于正、负励磁流量信号波形是关于零电势线对称的，正、负励磁信号作差后得到的最终流量信号等于正励磁流量信号采样值的两倍。则最终输出流量值Eout为

(8)

(8)式表明，Eout包含稳态分量Eos、非稳态分量Eod2个部分。其中，Eod是由“变压器效应”、涡电流引起的微分干扰、同相干扰及励磁电流不稳定等综合作用引起的，并与励磁频率、信号采样时序有关；Eos是根据法拉第电磁感应定律得到的理想值，与流速v、磁感应强度B成正比。

3.2信号模型参数的辨识

1)传感器选定后，励磁线圈确定，传感器口径D，Ki，Rx，Lx均作为已知量。转换器的励磁电路确定，Ue，I0给定，进而得到tp。

2)在零流速时，并将励磁电流方程(1)代入，则正励磁(或负励磁)流量信号的基本方程E1为

(9)显然，流量信号的开始时刻存在一个峰值(正励磁)或谷值(负励磁)，此后按照指数规律变化，直至进入稳态。且正、负励磁的变化过程是一致的，其变化的时间常数、峰(谷)值与励磁频率、流速等无关。(9)式可进一步简化为

(10)(10)式中：k为实际时间常数；An为峰值或谷值。由于励磁电路的开关管、恒流模块等与传感器串联，因此，k与理论时间常数Rx/Lx存在差别。An实质上是反映了微分干扰、同相干扰的强度。通过提取正励磁或负励磁的实际流量信号波形，分别测量峰值、谷值可得到An，再使用曲线拟合方法得到k。

3)An测得后，则流量值方程(8)可表示为

(11)

显然，上述参数均已知，可进行零点漂移的预测和基本误差的估计。

3.3零点漂移预测

根据(11)式，零流速时流量信号为

(12)

由此可见，零流速时Eout反映了零点的稳定性。由于微分干扰、同相干扰及励磁电流不稳定等影响，仪表输出存在漂移，且与励磁频率有关，这与文献[8]的研究是一致的。在传感器和励磁系统确定后，Eout仅与励磁频率f有关，因而可预测不同励磁频率相对应的零点漂移。

3.4基本误差的估计

基本误差直接反映了仪表的基本精度。可通过信号模型对不同励磁频率的基本测量误差进行估计。根据(11)式，任意励磁频率f在流速v时的不稳定分量Eod所引起的基本误差δ为

(13)

在传感器和励磁系统确定后，v一定时，δ仅与f有关。在实际仪表精度标定中，一般会取多个流速点，因此，在基本误差估计中，要与实际测量选取的流速点一致。

4仿真与实验

4.1模型仿真

为了验证文中所提的流量信号模型，本文基于MATLAB对流量信号波形进行了仿真。其中，励磁频率f=12.5Hz，传感器参数D=50mm，Rx=60.4Ω，Lx=498mH，励磁系统参数Ue=20V，I0=200mA，流速v=3m/s。图3a为波形仿真结果。

图3b为在v=3m/s，Kv=500时，转换器输出的实际流量信号波形。显然，传感器输出的流量感应电势约为1mV(正、负励磁信号之差)，与仿真值2.8mV接近，且两者动态波形近似。并与文献[9]的研究结论基本一致，从而初步验证了信号模型的准确性。

4.2基本参数的辨识

1)文中测试的相关参数分别为D=50mm，Rx=60.4Ω，Lx=498mH，Ue=20V，Kv=500，Ki=0.000 005T/A。其中，D，Rx，Lx由传感器供应商给出，Ue，Kv在励磁电路和转换器电路中设定。根据磁场的高斯定理，并忽略介质和传感器磁化强度为零，文中取Ki=I0μ0/D，其中，μ0为真空电导率。

2)先由示波器获取流量信号的波形，分别测取正、负励磁的峰值和谷值。再使用MATLAB拟合工具箱提取k。并以确定系数R来评价拟合效果，R取值为[0 1]，越接近1，表明数据拟合较好。

图3　12.5 Hz流量信号仿真波形Fig.3　12.5 Hz flow signal waveform in theory

实验的转换器采用了发明专利“基线放大处理方法”[14]，即先对信号的基线负反馈调整，再不失真放大，转换器给定的基线约1.25V。测试数据如表2和表3所示。

表2　正励磁信号的分析结果

表3　负励磁信号的分析结果

表1数据表明，各励磁频率的正励磁峰值An(尖峰值与稳态值之差)中最大偏差为1.69%(参考量为5个峰值的均值)，时间系数最大偏差为1.44%(参考量为5个时间系数的均值)，且R 接近1，显示拟合效果较好。表2数据表明，各励磁频率的负励磁谷值中最大偏差为2.40%(参考量为5个谷值的均值)，时间系数中最大偏差为1.75%(参考量为5个时间系数的均值)，且R 接近1，显示拟合效果较好。

从而表明流量信号中正、负励磁分别产生的An，k基本一致，证明了矩形波励磁数学模型是可行，且模型参数辨识方法有效。其中，正、负励磁k和An的差异是由实际正、负励磁不完全对称引起的。

4.3零点漂移预测

文中在DN50传感器上进行了零点漂移预测与测试实验，测试结果如图4所示。

实验结果表明，理论零点漂移值与实际测得值最大偏差为1.48 mm/s，最小偏差0.29 mm/s。零点漂移预测值与实际测得值的变化趋势基本吻合。从而表明零点漂移预测是可行的，进一步表明文中提出的信号模型在零流速条件下是准确的。

4.4基本误差估计

文中进行了仪表精度标定实验(清水上)，测量不同励磁频率f的基本误差(仪表精度)。传感器、励磁系统和转换器不变，f分别取3.125，6.25，12.5，75 Hz等。标定方式使用绝大多数电磁流量计厂家使用的实流标定方式[15]，具体检定电磁流量计样机的频率输出。图5、图6分别为流速v=1.4 m/s和2.8 m/s时，在DN50传感器上的测试结果。

图5结果表明，实际测得值与理论计算值之间的偏差最大为0.270%，最小为0.099%，平均为0.113%。且基本误差与实际测得值随励磁频率f变化的趋势基本一致。

图6　流速v=2.8 m/s的基本误差测试Fig.6　Basic error test under v=2.8 m/s

图6结果表明，实际测得值与理论计算值之间的偏差最大为0.117%，最小为0.027%，平均为0.070%。且基本误差与实际测得值随励磁频率f变化的趋势基本一致。

本文也在DN100传感器上进行了实验，结果与上述结论类似。在v=1.4 m/s时，实际测得值与理论计算值之间的偏差最大为0.666%，最小为0.069%，平均为0.251%。在v=2.8 m/s时，实际测得值与理论计算值之间的偏差最大为0.211%，最小为0.009%，平均为0.103%。从而说明，文中提出的信号模型在基本误差估计方面是有效的，并进一步验证了信号模型的准确性。

5结束语

本文对矩形波励磁的信号模型进行了研究。首先对矩形波励磁模型进行了分析，从励磁电流一般方程着手，引入了传感器磁路参数和励磁系统参数，再根据微分干扰、同相干扰与磁感应强度的关系，将其量化，进而建立了矩形波励磁模型。针对传统信号模型忽略信号采样的问题，本文基于励磁电流，模拟电磁流量计信号采样过程，得到了流量信号的基本方程。与传统信号模型相比，该模型与传感器、励磁系统、转换器信号采样有关，从而更符合实际情况。文中从信号波形仿真、模型参数辨识、零点漂移预测及基本误差估计方面进行了实验，实验结果表明，该模型符合实际，能够准确预测零点漂移和估计基本误差。从而为电磁流量计的性能研究提供了一种辅助手段，有效地提高了研究效率。

参考文献：

[1]SHERCLIFF J A. The theory of electromagnetic flow measurement[M].British: Cambridge University Press, 1962.

[2]李斌，田才东.电磁流量计的动态响应与零点稳定性[J]. 自动化仪表，1991，12(9) : 14-18．

LI Bin，TIAN Caidong． Dynamic response and zero-point stability of the electromagnetic flowmeter[J]． Process Automation Instrumentation，1991，12( 9) : 14-18．

[3]LIANG Liping, XU Kejun, XU Wei. SWT based separation method for periodic signal with non-stationary noise and its application in EMF[J]. Flow Measurement and Instrumentation, 2015(42):78-88.

[4]杨双龙, 徐科军, 梁利平, 等.基于DSP 的浆液型电磁流量计的研制[J]. 仪器仪表学报，2011，32(9) : 2101-2107.

YANG Shuanglong，XU Kejun，LIANG Liping，et al. Development of DSP based slurry-type electromagnetic flowmeter[J]. Chinese Journal of Scientific Instrument, 2011,32(9): 2101-2107.

[5]HEMP J, YOUNGS I. Problems in the theory and design of electromagnetic flowmeters for dielectric liquids. Part 3a.Modelling of zero dirft due to flux linkage between coil and electrode cables[J].Flow Measurement and Instrumentation, 2003(14):65-78.

[6]XU Kejun, WANG Xiaofen. Signal modeling of electromagnetic flowmeter under sine wave excitation using two-stage fitting method[J]. Sensors and Actuators, 2007(136):137-143.

[7]周真，王强，秦勇. 电磁流量计极间信号干扰的建模与分析[J]. 测试技术, 2012, 31(1):132-134.

ZHOU Zhen，WANG Qiang，QIN Yong.The Modeling of Electromagnetic Flow Meter’s Original Signals[J].Measurement & Control Technology,2012,31(1):132-134.

[8]SAITO OK. SAKURAI Y, OKAYAMA T. Study on Stabilized Zero-point of Electromagnetic Flowmeter with Rapid Excitation[J]. Instrumentation and Measurement Technology Conference, 1994, 5(2): 829-832.

[9]邬惠峰,严义,吴红娉.基于ANSYS的电磁流量计建模研究[J].仪器仪表学报, 2008, 29(2): 372-376.

WU Huifeng, YAN Yi, WU Hongping. Research on electromagnetic flow metermodeling based on ANSYS[J]. Chinese Journal of Scientific Instrument, 2008, 29(2): 372-376.

[10] JAKUBOWSKI J, MICHALSKI A. Signal Model Based Estimation of Flow Parameters for the Need of the Electromagnetic Measurement in Open Channels[C]∥Institute of Electrical and Electronics Engineers． Proceedings of the 2006 Instrumentation and Measurement Technology Conference． Italy: Institute of Electrical and Electronics Engineers，2006: 2024-2027．

[11] ZBIGNIEW W, JACEK J, ANDRZEJ M. Electromagnetic Flow meters for open channels:Current state and development prospects[J]. Flow Measurement and Instrumentation, 2015(42): 16-25.

[12] 蔡武昌, 马中元, 瞿国芳,等.电磁流量计[M]. 北京：中国石化出版社，2004: 147-151.

CAI Wuchang, MA Zhongyuan, ZHAI Guofang, et al. The electromagnetic flow meter [M ]. Beijing: China Petrochemical Press, 2004: 147-151.

[13] 王肖芬，徐科军. 正弦波励磁方式电磁流量传感器信号建模及模型验证[J]. 电子测量与仪器学报, 2009,468-473.

WANG Xiaofen, XU Kejun. Signal Modeling and model validating of Electromagnetic Flowmeters under Sine Wave Excitation[J]. Journal of Electronic Measurement and Instrument, 2009(2): 468-473.

[14] 李斌, 曹金亮, 史骥. 电磁流量计信号放大处理方法:中国，ZL200510028474.8 [P].2007-12-26.

LI Bin，CAO Jinliang，SHI Ji. Signal amplification processing method for electromagnetic flowmeter: China，ZL200510028474.8 [P].2007-12-26.

[15] 傅新，胡亮，谢海波，等.电磁流量计干标定技术[J].机械工程学报, 2007, 43(6):26-27.

FU Xin，HU Liang，XIE Haibo ，et al. Dry Calibration Technique of Electromagnetic Flowmeters[J]. Chinese Journal of Mechanical Engineering, 2007, 43(6):26-27.

DOI：10.3979/j.issn.1673-825X.2016.04.008

收稿日期：2015-07-09

修订日期：2016-03-03通讯作者：李新伟zzlydw@163.com

基金项目：高等学校博士学科点专项科研基金(20123108110011)

Foundation Item：The Research Fund for the Doctoral Program of Higher Education of China(20123108110011)

中图分类号：TN973.3;TP212

文献标志码：A

文章编号：1673-825X(2016)04-0487-07

作者简介：

李新伟(1988-)，男，安徽人，硕士研究生，主要研究方向为电磁流量计信号处理方法。E-mail：zzlydw@163.com。

李斌(1955-)，男，上海人，教授，研究方向为智能传感器与检测技术、仪器仪表与自动化装置。E-mail：sulibin@online.sh.cn。

(编辑：刘勇)

Signal model with rectangular wave excitation for electromagnetic flowmeter

LI Xinwei，LI Bin，ZHANG Xin，WANG Gaoyang，WANG Guanbing

(College of of Mechanical & Electronic Engineering and Automation, Shanghai University,Shanghai 200072, P.R. China)

Abstract:The traditional rectangular wave excitation model fails to take into account both the influence of the sensor magnetic circuit system and the excitation system simultaneously, and ignores the signal sampling process, thus, the signal model with rectangular wave excitation does not match the real conditions well. Based on the general equation of magnetic excitation current, a rectangular wave excitation model is proposed in this paper. This model demonstrates the mathematical relationship between the magnetic flux density and the relative parameters of magnetic circuit system and magnetic excitation system,and quantifies the differential interference and in-phase interference. On the basis of the proposed magnetic excitation model, a flow signal model with rectangular wave magnetic excitation is constructed via simulating the signal sampling process in electromagnetic flowmeter, and an identification method for the model parameters is also presented. A simulation experiment of flow signal and three practical experiments including model parameter identification, zero-point drift prediction and basic error estimation were carried out. The experimental results show that the maximum zero drift prediction error is 1.48 mm/s, and the maximum basic deviation is 0.270%.

Keywords：electromagnetic flowmeter; signal model；rectangular wave excitation；zero-point drift；basic error