基于大变异遗传算法的直升机甲板组合优化

王天玥，孟凡磊

（1. 大连理工大学 船舶工程学院，辽宁大连 116023；2. 海油发展安全环保分公司，天津 300456）

基于大变异遗传算法的直升机甲板组合优化

王天玥1，孟凡磊2

（1. 大连理工大学 船舶工程学院，辽宁大连 116023；2. 海油发展安全环保分公司，天津 300456）

建立了基于FORTRAN与ANSYS交互的结构优化模式，并通过大变异操作，避免了遗传算法自身出现“早熟”的现象。在此基础上，以FORTRAN编写的大变异遗传算法程序作为优化平台，将ANSYS结构重分析得到的数据作为约束条件与优化平台交互，对某渔船的直升机甲板结构进行了静力和频率的组合优化，降低了甲板结构的重量。

直升机甲板；结构优化；大变异遗传算法；离散变量

0 引言

在生产生活和军事防御中，人们需要建造不同种类的结构物，例如巨型游轮、大型客机和航空母舰等。在设计这些结构时，工程师总是希望把它们设计的尽可能的“优”。在20世纪60年代前，由于结构设计的改进缺乏系统的指导方法，加上没有能够高效进行结构分析的计算工具，结构优化设计通常依靠工程师们积累的经验缓慢进行。1960年，Schmit［1］在结构优化首次中采用数学规划理论，同时采用有限元方法对结构进行分析，研究了多种受力情况下结构在弹性范围内重量轻量化的问题，形成了优化模式的基本雏形，标志着现代优化新模式的出现。

近年来，船体结构设计的优劣不仅直接影响船舶的综合性能和经济效益，而且由于不合理的结构设计引发的船舶故障或事故屡见不鲜，造成了不必要的经济损失，且因此优化设计在船体结构设计中具有重要的工程意义。

1 基于遗传算法的结构优化模式

1.1 遗传算法在结构优化中的应用

人们在研究自然界生物体的进化过程中，发明了仿生学优化方法：基因遗传算法（GA）、进化策略算法（ES）和神经网络算法（ANN）等。这些具有并行行为的智能优化算法，为具有非线性、多极值等特点的复杂函数及组合优化问题的求解提供了可能。其中，遗传算法适合于无表达式或有表达式的目标函数，且具有可实现的并行计算行为，对不同问题有很强的鲁棒性，因此在许多领域得到了广泛的应用［2］。

Schaffer［3］采用了多目标遗传算法（MOGA）对胞元结构进行了拓扑优化，并得到了较为优秀的Pareto解。马光文等［4］采用交迭变异型遗传算法，以桁架断面面积作为设计变量，在应力和位移约束条件下，对十支桁架进行了轻量化设计。Luigi等［5］采用位屏蔽指向性遗传算法，基于分析参数化板壳结构的改进有限步法，针对各向同性的对称截面薄板结构，分别进行了受压时的轻量化优化和屈曲载荷最大化优化。Marin等［6］采用基于全局搜索的遗传算法结合有限元，考虑了质量、湿热效应和应力条件，针对承受静压力的常规复合材料加筋板，进行了多目标优化。杜晓佳［7］分析对比了自适应进化策略算法和遗传算法的优缺点，并采用遗传算法针对船舶悬臂结构的隐身和动力特性进行了优化。Manudha等［8］采用实数编码的遗传算法，结合等几何分析的有限元法，考虑湿热效应，针对复合材料螺旋桨进行了多目标、多材料和多铺层厚度的优化。

1.2 基于FORTRAN与ANSYS交互的优化模式

通常在结构优化过程中，如果需要修改某些结构设计，必须先修改结构分析模型再进行计算分析，这显然影响了优化效率。通过商业软件ANSYS的结构优化模块进行处理，则可以不必完全重新修改模型，其前处理模块能够通过循环控制文件自动完成修改设计。但ANSYS提供的优化方法都是针对连续型设计变量，无法计算离散后的设计变量。此外，ANSYS结构优化模块无法求解设计变量个数大于60的优化问题，当设计变量个数超过其推荐值20时，可能会陷入到局部最优解［9］。因此，为了解决ANSYS中离散设计变量和特殊形式的目标函数的优化问题，本文以FORTRAN语言编写的大变异遗传算法程序作为优化平台，将ANSYS有限元重分析得到的数据作为约束条件与优化平台交互。

FORTRAN最大特性是接近数学公式的自然描述，在计算机里具有很高的执行效率。FORTRAN优化程序与 ANSYS结构分析的对接主要依靠Digital Visual FORTRAN提供的第三方扩展模块DFLIB（Digital FORTRAN Library）。通过DFLIB模块中的时变函数SYSTEMQQ，可以在FORTRAN优化程序中将ANSYS作为一个子程序调用：

PROGRAM MAIN

USE DFLIB

IMPLICIT NONE

……

LOGICAL（4） RESULT

……

RESULT=SYSREMQQ（COMMAND LINE）

……

END PROGRAM

其中，COMMAND LINE表示需要进行的CMD操作，是字符串形式，函数中的实际长度由传入的参数决定；RESULT为逻辑变量，如果调用成功为TRUE，否则为FALSE。

2 大变异遗传算法

2.1 提出背景

遗传算法虽然具有优良的寻优能力，但是“早熟”现象出现一直困扰着许多学者。当某代群体中某一个体的适应能力远远强于其他个体时，由于顶端优势的存在，其子代中大部分会来自于同一个父代，种群的多样性遭到了严重的破坏。顶端优势的极限情况就是子代全部个体都来自于相同的父代，即算法出现了“早熟”。

理论上来说，遗传算法中一旦出现“早熟”，选择和交叉操作就会失效。由于个体发生变异的可能性较小，因此“早熟”的群体无法通过变异操作来增加群体的多样性。虽然可以采用尺度化操作对个体适应度进行变换，但是这会改变原问题的适应度函数，降低遗传算法的收敛速度。

为了解决“早熟”问题，大变异遗传算法应运而生，它的基本思想是：当某代群体中全部个体的适应能力差别较小时，则用一个较大的随机概率来执行变异操作。执行大变异操作的遗传算法能快速增加“早熟”群体的多样性，使种群体继续向全局最优方向进化［10］。

2.2 大变异操作的实现

是否执行大变异操作依赖当前种群的成熟程度。种群中个体的最强适应能力与平均适应能力越接近，则种群越成熟。在成熟的种群中，每个个体的适应度趋向于一个相同的值。

当某代的最大适应度Fmax和平均适应度Favg满足aFmax＜Favg时（0.5＜a＜1.0被称为密集因子，表征个体的集中程度），将该代群体中的所有个体设置为具有最强适应能力的个体，随后以一个比通常变异概率大4倍以上的概率对该代个体进行大变异操作［10］。

遗传算法通过对种群中的个体连续的执行遗传操作来产生新个体，这种操作的执行是随机的。当群体中产生出优良性状的个体时，这种随机性会导致个体的优良基因片段被破坏。为了避免这种情况的发生，可以采用最优保存策略来保证个体的优良基因能够遗传到子代中。最优保存策略的具体过程如下［11］：

1）寻找目前群体中适应能力最强和最弱的个体；

2）判断目前群体中适应能力最强的个体是否比目前出现过的适应能力强的个体优秀，如果是，则以目前群体中适应能力最强的个体作为进化过程中最佳的个体；

3）在遗传操作作用群体后，保存的最佳个体将替换适应能力最弱的个体。

3 直升机甲板结构组合优化

直升机甲板结构是船舶结构的重要组成部分，其承受载荷复杂结构形式多样化。为追求船舶结构的优良性能，可以在保证直升机甲板满足设计要求的同时对其进行优化。某渔船的直升机甲板为横骨架式结构，用于直升机的降落和存放。本文根据中国船级社相关规范［12］，采用大变异遗传算法对其进行轻量化设计，以便降低结构建造成本。

3.1 甲板参数化模型

根据规范，采用壳单元（shell63）和梁单元（beam188），建立直升机甲板参数化模型。该直升机甲板的肋骨间距为600mm，材料为铝合金，弹性模量E=0.7×1011Pa，泊松比μ=0.3，密度ρ=2.8× 103kg/m3。在整个有限元模型的底端对节点的自由度进行约束。直升机降落位置如图1所示。

图1 直升机降落位置示意图

直升机甲板结构复杂，为了降低结构优化的成本，在不增加结构焊缝、不降低结构强度和不改变结构拓扑的原则下，确定了前端壁板、防尘板、72#肋位横舱壁、左舷4200纵舱壁、右舷4200纵舱壁、屋檐加强肘板、防尘板加强筋、首端壁水平扁钢、首端壁垂直扁钢及甲板开口加强筋为模型设计优化参数。其中板厚的取值集合Ω=｛6mm， 7mm， 8mm，9mm ｝；甲板上可选取的型材类型如表1所示。

3.2 优化的数学模型

考虑实际工程的经济性，选取直升机甲板的总体质量作为目标函数。在进行优化时，为了避免结构产生屈服现象，要求甲板结构必须满足强度条件。为了避免共振现象的产生，直升机甲板结构必须满足频率禁区要求。在对甲板进行强度校核时，考虑两种工况：直升机着陆工况和直升机系留工况，许用应力均为190MPa，如表2所示。

表1 骨材类型和尺寸

表2 直升机甲板各工况所受载荷

沿海中小型渔船主要的激振源是螺旋桨和主机。在对甲板进行频率校核时，充分考虑螺旋桨叶频、倍叶频、桨轴频和主机轴频以后，制定的频率禁区如表3所示。

表3 频率禁区

综上所述，直升机甲板组合优化的数学模型为：

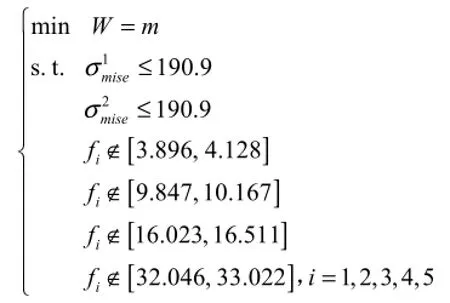
3.3 组合优化结果

直升机甲板结构复杂，为减少计算时间，可以针对问题的优化层次对模型进行数据库储存。本节进行的组合优化属于形状优化，算法在每次迭代时，没有改变甲板结构的几何尺寸和几何拓扑，可以将不变的甲板几何模型存储到ANSYS的数据库中。因此，在参数化甲板模型时，参数化的变量全部为有限元模型中的单元属性，并在每次寻优时直接修改有限元单元的属性。在对直升机甲板进行约束条件校核时，ANSYS主要计算了两种工况下结构的最大等效应力以及结构的前五阶固有频率。

甲板结构设计参数的初始值是根据每个离散设计变量的取值集合随机生成的。遗传算法由于自身的随机性，只有当大部分解都趋向同一值时才可认为是最优解。图2为直升机甲板结构质量在优化中的变化过程。其中横坐标为迭代次数N，纵坐标为直升机甲板的总体质量m（kg），图中3次不同初始点优化过程均收敛于7 247.291kg，与初始设计的质量7 511.343kg相比减轻了3.5%。直升机甲板结构初始设计和最终设计的参数取值如表4所示。两种工况下，直升机甲板结构最终设计的最大等效应力均小于初始设计，如表5所示。直升机甲板最终设计的前五阶固有频率仍然能够避开该渔船的频率禁区，如表6所示。

图2 直升机甲板质量大小变化

表4 直升机甲板最优结构的设计参数取值

表5 两种工况下的最大等效应力

表6 前五阶固有频率对比，单位（Hz）

4 结论

1）经过优化的最终结构具有更高的强度、更轻的重量。在甲板上，直升机无论着陆还是系留，最终结构的最大等效应力均小于初始结构。由于充分考虑了船上主要激励源的激励频率，结构最终设计的固有频率仍然能够较好地避开船上频率禁区。

2）针对问题的优化层次采取模型数据存储可以有效缩短程序运行的时间，对于实际工程中的复杂模型可以参考本文优化的简化思想，提高优化程序的应用性和可靠性。

3）本文提出的考虑离散变量的优化模式具有较强的通用性，可以应用于工程实际结构优化设计，并且能够扩展去解决结构隔振和晃荡响应等对船体结构构成约束的优化问题。

［1］ Schmit L A. Structural design by systematic synthesis［C］//ASCE. New York， 1960.

［2］ 程耿东. 工程结构优化设计基础［M］. 大连： 大连理工大学出版社， 2012.

［3］ Schaffer J D. Multiple objective optimization with vector evaluated genetic algorithms［C］//DBLP. Pittsburgh， PA，USA， 1985.

［4］ 马光文， 王黎. 遗传算法在桁架结构优化设计中的应用［J］. 工程力学， 1998， 15（2）： 38-44.

［5］ Luigi I， Eugenio R. Optimum topological design of simply supported composite stiffened panels via genetic algorithms［J］. Computers and Structures， 2008， 86： 1718-1737.

［6］ Marín L， Trias D， Badalló P. Optimization of composite stiffened panels under mechanical and hygrothermal loads using neural networks and genetic algorithms［J］. Composite Structures， 2012， 94： 3321-3326.

［7］ 杜晓佳. 舰船悬臂结构隐身与动力特性优化［D］. 大连理工大学， 2013.

［8］ Manudha T H， Natarajanb S， Gangadhara P B. Isogeometric analysis and Genetic Algorithm for shape-adaptive composite marine propellers［J］. Computer Methods in Applied Mechanics & Engineering， 2015， 284： 835-860.

［9］ 刘益铭， 刘大洋， 刘山洪. 基于 MATLAB联合ANSYS的斜拉桥恒载索力优化［J］. 重庆交通大学学报： 自然科学版， 2013， 33（6）： 1111-1114， 1194.

［10］ 马钧水， 刘贵忠， 贾玉兰. 改进遗传算法搜索性能的大变异操作［J］. 控制理论与应用， 1998， 15（3）：404-408.

［11］ 玄光男. 遗传算法与工程设计［M］. 吉林： 科学出版社， 2000.

［12］ 中国船级社. 钢质海船入级规范［S］. 北京： 人民交通出版社， 2009.

Combinational Optimization of Helicopter Deck Based on Genetic Algorithms with Cataclysmic Mutation

Wang Tian-yue1， Meng Fan-lei2
（1.Department of Naval Architecture and Marine Engineering， Dalian University of Technology， Dalian 116024， China； 2.CNOOC Enertech Safety & Environmental， Tianjin 300456， China）

The structure optimization pattern is built based on mutual FORTRAN and ANSYS. The “early-maturing” phenomenon in the genetic algorithms is successfully avoided by adapting the cataclysmic mutation. On the basis， a helicopter deck is optimized on the structure with static and frequency constrains by giving the result of finite element reanalysis of ANSYS to the genetic algorithms with cataclysmic mutation written by FORTRAN， reducing the weight of the deck structure.

helicopter deck， optimization of structure； genetic algorithms with cataclysmic mutation；discrete variables

U661.43

A

10.14141/j.31-1981.2016.01.004

王天玥（1989—），女，硕士，研究方向：船舶结构动力优化。