基于ANSYS的响应曲面优化在船舶甲板支柱线性屈曲分析中的应用

黄 技，吕鸿冠，严 谨，叶剑钊

（广东海洋大学 工程学院，广东湛江 524088）

基于ANSYS的响应曲面优化在船舶甲板支柱线性屈曲分析中的应用

黄 技，吕鸿冠，严 谨，叶剑钊

（广东海洋大学 工程学院，广东湛江 524088）

随着有限元技术和计算机软硬件的迅速发展，结构优化设计的理论和算法均得到巨大的飞跃，并越来越受到工程师的重视。利用ANSYS的Static Structural模块和Design Exploration模块，在考虑压杆稳定的情况下，对船舶甲板支柱进行线性屈曲分析，得到一阶线性屈曲因子后，对其进行结构优化，通过对优化数据的分析对比，得到支柱结构的最优化方案，在现实工程应用中具有一定的指导意义。

结构优化设计；线性屈曲；压杆稳定；船舶支柱

0 引言

优化设计的概念起源于人们的社会生产实践活动。当一个产品设计或一项工程结构不能满足实际需求时，设计师或工程师往往会依照前人或自己累积的经验，遵循一定的“优化思想”和“优化原则”，通过采用不同的方法，不断改变设计模型和设计变量，从而改善产品或结构的各项性能指标，使设计达到最优化。

本文通过ANSYS的Static Structural模块，在考虑压杆稳定的情况下，对船舶甲板支柱进行线性屈曲分析，得到一阶线性屈曲因子后，利用一阶性线性屈曲因子与特征值（预应力）的关系，求出屈曲极限，并在Design Exploration模块中的Response Surface对支柱进行结构优化，通过对设计变量和目标函数的分析对比，得到支柱结构的最优化方案，在现实工程应用中具有一定的指导意义。

1 优化理论

1.1 结构优化的数学模型

1.1.1 设计变量

对一个工程结构进行优化设计，首先应根据与性能指标密切相关的基本设计参数对结构进行数学建模。在数学模型中，部分设计参数是动态的，需要在优化方程中求解。在这部分参数中，线性独立的设计参数称为“设计变量”。结构优化的目的就是要在满足预先指定的限制条件（约束函数）中，寻找设计变量的最优解。

1.1.2 目标函数

在对结构进行优化设计过程中，至少有一个衡量优化结果优劣的函数，称为目标函数。除了目标函数外，还有对结构性能和设计指标进行限制的约束函数，保证结构设计在合理范围内。如果优化设计只有单个目标函数，称为单目标优化，如果目标函数不止一个，称为多目标优化。单目标结构优化设计的数学模型如下［1］：

寻找一组设计变量：

使目标函数：

且满足约束条件：

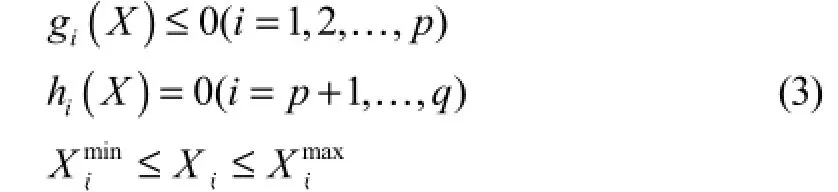
式中：F（X）称为目标函数；gi（X）称为不等式约束函数；hi（X）称为等式约束函数；X称为设计变量列向量；称为设计变量Xj取值的下限和上限。

如果X=［X1X2X3… Xn］T满足所有约束条件，则称其为可行解或可行点，所有可行点组成的集合称为可行域。使目标函数值最小（或最大）的可行解即为最优解。

1.2 屈曲分析理论

设结构的应力刚度矩阵［S］是基于膜应力的任意基准强度。在线性条件下，［S］和通常的刚度矩阵［K］为位移的函数。如果基准条件下的位移矩阵｛D｝加上虚位移矩阵｛φ｝，而作用的载荷［F］保持不变，那么为了使状态｛D｝和｛D+φ｝保持平衡，必须满足：

式中，［K］为刚度矩阵；［S］为应力刚度矩阵；｛φ｝为虚位移矩阵；λ为特征值（也成为比例因子或载荷因子）。虚位移矩阵｛φ｝代表模型的屈曲形状，也称为屈曲模态。在通常的屈曲分析中，一般只对结构的第一个特征值和特征矢量感兴趣。由于特征值不考虑任何非线性和初始扰动，所以它只是一种理想解。

2 优化模型与方案

本文采用的优化模型是无人的非自航的箱形驳船的甲板支柱［2］，根据中国船级社2012年《钢质海船入级与建造规范》的要求进行计算后，得出甲板支柱最大受力为598kN。在这里，选择受力最大的情况，即598kN作为约束条件。则所用钢管的受力极限必须满足式（7）。

通过查询国标无缝钢管规格表，在这里选择Φ219×15规格的无缝钢管作为起始的船舶支柱材料。接下来，先通过ANSYS的Geometry模块建立钢管的几何模型，将模型导入Static Structural模块求解，得到一阶屈曲因子，根据一阶屈曲因子判断所选材料的屈曲极限是否满足式（7），若不满足，重新选择钢管规格，重复上述步骤；若满足，则用Design Exploration模块进行优化，从而得到最经济实用的结构设计方案。整个过程的流程如下：

1）通过ANSYS Static Structural进行结构静力学分析；

2）根据一阶屈曲因子判断Fs≥598kN是否成立；若成立，进入3）；不成立，重新选择钢管型号重复1）；

3）设置优化变量，进入Design Exploration进行优化；

4）分析对比优化结构，选择最优方案；

5）利用新的型号计算屈曲极限，查看是否满足要求。

3 ANSYS结构静力学分析

3.1 前处理及预应力分析

利用ANSYS的Geometry模块对Φ219×15规格的无缝钢管进行几何建模，模型的材料为默认的Stainless Steel（不锈钢）。建模过程中，将内径设为优化参数 P5-Inner Diameter。将建好的模型导入Static Structural模块的Mesh进行网格划分，将网格大小设置为0.01m。网格划分完毕后，共有30124 个Nodes（节点），4564个Elements（有限单元）。

将甲板支柱的工作状态抽象为一端为固定约束，另一端是自由端的力学模型。在这里，把钢管底面添加Fix Support（固定端约束），钢管的顶面施加1000N的Force（预应力），并将几何体的Mass（重量）设为优化参数P2-Solid Mass，结果如图1和图2所示。设置好其他参数后，对模型进行预应力分析，分析结果如图3和图4所示。

图1 固定端约束

图2 预应力的大小和方向

图3 1 000N预应力下的应力分布云图

图4 1 000N预应力下的应变分布云图

从上面的结果可以看出，应力主要集中在钢管底部，而总应变主要集中在钢管顶部，且总应变非常小，最大总应变只有2.08×10-6m。上述分析结果是在预应力为1 000N的情况下求解出来的，不具备实际的工程应用价值。

3.2 线性屈曲分析

通过上面的分析可以看出，根据式（6），只要能求出钢管的一阶屈曲因子，便可计算钢管的屈曲极限。将Static Structural模块与Linear Buckling模块进行数据关联，设置屈曲模态为六阶模态进行求解，求解后的屈曲因子如表1所示。

表1 不同模态的屈曲因子

从表1可以看出，一阶与二阶，三阶与四阶，五阶与六阶对应的屈曲因子几乎相同，故这里只取第一、三、五阶进行分析。通过模态云图（图 5、图6、图7），可以直观地看出不同模态下钢管的变形情况。

图5 一阶屈曲分析结果

图6 三阶屈曲分析结果

图7 五阶屈曲分析结果

从上面不同阶的分析结果可以看出，模态阶级越大，变形越大，根据前面理论部分的分析可知，只需关注第一阶的分析结果即可。通过表1可知，一阶线性屈曲因子为1 548.3，则在式（6）中：

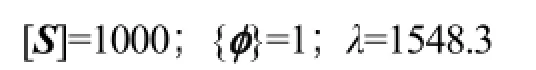
将上述三个数值代入式（6），可求得：

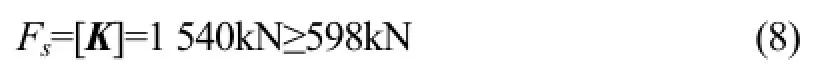
故所选的无缝钢管Φ219×15符合结果要求。且1 540kN/598kN=2.58，说明结构仍具有很大的优化空间。这里，一阶屈曲因子设为优化参数 P3-Total Deformation Load Multiplier。

4 结构优化

4.1 优化方案

根据上面的结果，可知Φ219×15规格的无缝钢管的屈曲极限1 540kN完全满足实际需要，且对于598kN来说仍有很大的优化空间。船舶甲板支柱在工作状态下是受压的二力杆，根据材料力学理论［4］，提高压杆稳定性措施主要有：1）选择合理的截面形状；2）改变压杆的约束条件；3）合理选择材料。

显然，对于船舶甲板支柱的优化，只能通过改变截面来进行。在这里，选择对壁厚进行优化设计。对壁厚进行优化，其本质上是改变横截面的表面积，在保证屈曲极限不低于598kN的情况下，使结构质量减轻，得到最优化方案。优化参数经过整理分析后如表2所示。

表2 优化参数类型

4.2 优化结果

进入ANSYS的Design Exploration模块，将设计变量P5-Inner Diameter的范围设置为179～199，得到的设计点参数如表3所示。

做好其它相关设置后，开始进行优化分析。分析结果如图8和图9所示。

从图8可以看出，结构质量随着内径的增加呈线性递减的趋势。从图9可以看出，Design Point 3在所有设计点中内径是最大的，且质量也是最小的，故Design Point 3是理想的方案。通过分析结果可知Design Point 3的参数和未优化前的参数对比如表4所示。

图8 质量与内径的关系

图9 不同设计点的质量分布

表4 优化前后的对比

通过图10和图11的Spider图，可以清晰地看出优化前后两者的区别。

图10 优化前的Spider图

图11 优化后的Spider图

从图10和图11可以看出，优化后虽然应力相对优化前大大增加，但是总质量和一阶屈曲因子也随之下降，下面通过计算来验证优化方案是否可行。根据上面分析的结果，可知：

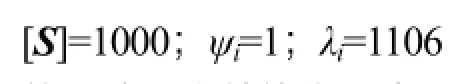
将上述三个数值代入式（6），可求得：

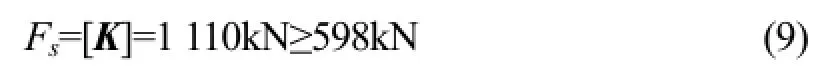
满足Fs≥598kN。优化后的总质量206.17kg，优化前的总质量301.86kg，则：

式中，δ是材料节约比率。

从上述分析可以看出，结构优化后，屈曲极限仍满足工程需求，且总质量只有优化前的68.3%，大大降低了工程成本。

5 结论

本文以结构优化理论和屈曲分析理论为基础，建立船舶甲板支柱的结构优化模型，通过ANSYS Static Structural模块和Design Exploration模块对甲板支柱结构进行优化。优化结果表明，在满足屈曲极限大于极限工作应力的前提下，支柱壁厚减少了10mm，结构质量只有原来的68.5%，极大降低了成本，在现实应用中具有一定的参考价值。

［1］ 王栋. 结构优化设计-探索与进展［M］. 北京：国防工业出版社， 2013.

［2］ 黄志新， 刘成柱. ANSYS Workbench 14.0超级学习手册［M］. 北京： 人民邮电出版社， 2013.

［3］ 黄志新， 刘成柱. ANSYS Workbench 14.0超级学习手册［M］. 北京： 人民邮电出版社， 2013.

［4］ 刘鸿文. 材料力学I［M］. 第5版. 北京： 高等教育出版社， 2010.

［5］ 屠凤莲. 基于ANSYS的支撑架特征值屈曲分析［J］.河北工业大学学报， 2010，39（3）： 6-10.

［6］ 江晓峰. 有限单元法之梁柱单元的屈曲分析精度［J］. 结构工程师， 2010，26（5）： 20-25.

［7］ 余娟. 基于ANSYS的天线杆屈曲分析［J］. 计算机与数字工程， 2013，41（9）： 1523-1528.

Application of Response Surface Methodology in Linear Buckling Analysis of Optimization of Ship Pillar Based on ANSYS

Huang Ji， Lv Hong-guan， Yan Jin， Ye Jian-zhao
（Guangdong Ocean University， Guangdong Zhanjian 524088， China）

With the rapid development of FEM technology and computer software & hardware， the structural optimization theory and algorithms have great progress and development， so more and more engineers pay attention to it. In the paper， using the Static Structural module and Design Exploration module of ANSYS and considering the column stability， the linear buckling analysis of the ship pillar is done. After the first-order linear buckling factor is gained， the structure is optimized. Through the analysis and comparison of the optimizing data， the best structure optimization scheme of pillar structure is gained. It is significant to the real engineering applications.

structural optimization； linear buckling； column stability； ship pillar

U661.43

A

10.14141/j.31-1981.2016.01.007

广东省青年创新人才类项目（2014KQNCX086）。

黄技（1988—），男，助教，研究方向：船舶结构设计。