高中物理学习培养建模思想的几点思考
邹译达

我们高中生都说物理难学!为什么?笔者在学习过程中发现,目前的物理题往往有具体的情境,我们首先要突破的困难是“建模”,“物理模型”是在物理研究中对相关状态或过程进行概念化的表征方式.一旦学会了构建物理模型,那么很多物理问题其实就不难了,建模是一项重要的科研能力,也是一种典型的物理思想.高中物理学习的过程中,如何培养建模思想和提升建模的能力呢?笔者认为可以从以下几点着手.
1 自主提升建模思想的理论支撑
学习是复杂的,是具有艺术性的科学活动,那么对于高中物理学习培养建模思想有着怎样的教育理论支撑呢?笔者认为建模并非一蹴而就,具有过程性和阶段性,笔者认为皮亚杰认知发展理论可以作为培养、提升建模思想的理论支撑.
皮亚杰的认知发展理论认为儿童的认知发展具有四个不同的阶段,分别是感知运动阶段、前运算阶段、具体运算阶段、形式运算思维阶段.这四个阶段有这样四个特征:第一,每一个阶段都有独特的认知图式,在不同的年龄阶段呈现出阶段性.第二,这四个阶段出现的先后顺序是恒定不变的,都是由前一个发展阶段进入到下一个发展阶段,逐渐达到最高水平.但是每个儿童的发展快慢却是有差异的,同年龄段之间的联系并不是固定不变的.由于受先天智力、后天的社会环境、所受文化程度等的不同而有着个体的差异.第三,每一个阶段的发展都是在前一个阶段的发展基础之上形成的.第四,每个阶段的发展与前一阶段有交叉重叠,在准备期内,同前一阶段保持密切的联系.
皮亚杰还深刻阐明了影响儿童心理发展的四个基本因素.最基本的因素是个体的成熟.成熟为心理的发展提供了可能性.其次是个体的练习和经验.通过个体的反复动作练习、习得经验,促使其认知不断发展.然后是社会经验.主要指社会文化经验和人际交互作用.最后是平衡过程.
回顾我们物理建模的过程,与这个四个阶段非常符合,需要我们在不断地练习、分析和反思的过程中才能将建模的经验用于解决实际问题中来,并在不断平衡的过程中内化为自己的知识.
2 具体的实践策略分析
2.1 重视过程体验在建模学习中的作用
建构物理模型的过程是将感性信息升华为理性认知的重要过程,属于一种科学抽象的处理手段.我们学习物理模型的构建过程时,可以沿着前人的探索思路重新感悟知识的形成和完善过程,并从中发现、领会和掌握物理模型的构建方法.如果以传统意义上的题海战术来让我们学习并熟悉物理模型,其短、平、快的特点表面看来节省了学生的精力和时间,但是严重压缩了我们学生的认知过程,让我们没有充分感悟,直接导致我们对模型的认知相当肤浅.结果是我们根本无法把握模型的实质,只能靠生搬硬套来解决相关问题.
例1 如图1所示的铁芯上绕有两组线圈,匝数分别为n1=800、n2=200,若在上侧线圈的两端加上u=51sin314t V的交变电压,并将交流电压表接在下线圈两端,则电表示数可能为
A.9.0 V B.2.0 V
C.144.0 V D.12.7 V
处理上述问题时,很多学生选择了9.0 V,其原因是生搬硬套“理想变压器”这一模型的结论,没有认真比对试题模型与理想模型间的差别,而其根源就在于我们在新课学习的过程中忽略建模思想的有序培养.因此这就提醒我们,学习过程应该让合作探究,全面参与建模过程,而不是仅仅等待教师嚼碎了灌输,我们学生应该在自我领悟中感受模型的构建.
以理想电压表模型的构建为例,我们通过以下步骤几个步骤进行探索并建立模型:(1)结合可拆变压器进行实验,首先选用匝数比恰当的原副线圈和电压输入,让副线圈所接灯泡正常发光,然后尝试着拿走变压器上的横条铁芯,对比铁芯闭合和非闭合状态下灯泡的明暗情形,再针对现象的思考和讨论中感悟铁芯闭合的作用;(2)将输入电压调成2 V,先以100匝和200匝的原副线圈来进行实验,小灯泡正常发光,再将副线圈调整为800匝,灯泡却熄灭了.这一现象超出大家的想象,有所预习的学生都清楚匝数越大,副线圈的电压越大,灯泡应该更亮,为何结果相反呢?我建议大家用电压表对灯泡两端的电压进行测量,可以发现读数很小,但是断开灯泡,直接测量副线圈两端电压,示数却很大,基本接近匝数比,经过上述实验,再联系有关闭合电路的欧姆定律,线圈内阻的影响基本浮出水面;(3)我们可以直接用手触摸已经工作一段时间的铁芯,大家会感受到铁芯在工作过程中热量的生成,然后在相互讨论用彼此绝缘的硅钢片叠起来组成铁芯的优点.通过上述过程,学生就能把握住理想变压器建模过程的基本要点,只有在此基础上探索相关特点,才能从本质上理解模型的内涵.
2.2 重视原始问题在建模学习中的作用
当前的高中物理STSE是核心素养之一,所以我们遇到的很多物理习题都源自于原始物理问题,所谓原始物理问题,就是指那些从自然界或生活生产中直接提取而未经过加工提炼的物理问题.它是对客观实在直接而朴素的反映,其对现象的描述未做任何科学化的整理,更没有像物理习题一般将已知量和所求量直接罗列出来.而当前教学中所采用的物理习题,属于抽象式物理问题,是教师在对原始物理问题进行了提炼、简化和抽象而来的产物.也正是由于我们学生面对的大都是这类精加工处理的物理问题,跳过了由原始物理问题到抽象物理问题的建模过程,使得我们在建立模型方面出现严重缺失,最终我们的学习只能被限制在套用模型的层面.由此可见,建模过程是将原始物理问题发展为抽象物理问题不可或缺的步骤,就我们的物理学习而言,这一过程不容逾越.所以,实际的物理学习过程中,要关注原始物理问题,教师给我们提供原始物理问题不是为了为难我们,这些问题都很有趣,大大改善了单一化习题训练模式,我们要对相关问题进行提炼和处理,才能有效提升模型构建能力和理解能力.
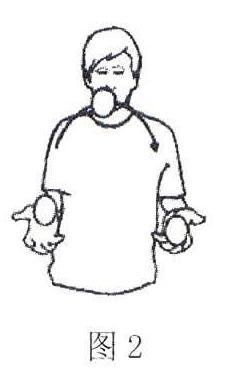
例2 如图2所示的杂技演员正在进行表演,请结合图形估算这个演员抛出一枚鸡蛋的过程中,所做功的数值最接近
A.0.3 J B.3 J
C.30 J D.30 J
本题与一般的物理习题有着明显的差别:题目中没有给定问题解决所需要的物理量数值,没有直接的模型说明,更没有明确考核的规律和方法,因此本题是一个典型的原始物理问题.相关问题的解决需要如下过程:首先明确对应的事实和现象是怎样的一个问题,从而在此基础上对其进行分析和简化,进而抽象出物理模型,最后在提炼和加工的过程对有关物理量的信息进行发掘,进而使之转化为大家所熟悉的抽象物理问题.本题作为一道估算题,将鸡蛋的运动形式视作竖直上抛运动或斜抛运动对结果并无较大影响,至于上抛过程中鸡蛋各部分的运动特点也属于该问题 中的次要因素,因此在忽略次要因素的基础上,可以提取出模型:竖直上抛的质点.再结合生活实际,将鸡蛋的质量(0.05 kg)以及鸡蛋上升高度约为人体身高的三分之一(0.6 m)代入模型,能很快锁定答案.但是如果将问题改成:一枚质量为0.05 kg的鸡蛋,竖直上升的最大高度为0.6 m,求解人抛起鸡蛋过程中的做功,这样的题目就显得单薄而肤浅了.正因为试题没有直接给出经过加工处理的已知和模型,因此才给试题盖上了神秘的面纱,大家需要充分发挥自己的抽象思维,对相关条件进行挖掘,才能有效解题,这充分体现了高考命题能力立意的基本思想.
总之,解决问题的过程是不断构建物理模型并应用物理模型提取解决问题方法的过程,我们在培养自我建模能力时,应该深入研究最基础、最典型物理知识、物理问题及研究方法,在解决问题的过程思考、感悟物理模型,体验“形成概念,探究规律”的过程,唯有如此,才能深入掌握探究物理问题的基本方法,使解决物理实际问题的能力得到有效提高.

