用于IGBT模块动态电热耦合仿真的损耗模型优化
刘 任 唐 波 孙 睿 吴 卓 江浩田
(三峡大学 电气与新能源学院, 湖北 宜昌 443002)
用于IGBT模块动态电热耦合仿真的损耗模型优化
刘任唐波孙睿吴卓江浩田
(三峡大学 电气与新能源学院, 湖北 宜昌443002)
摘要:绝缘栅双极晶体管(IGBT)模块动态电热耦合仿真分析的关键问题是损耗模型的准确建立.本文减少通态损耗模型线性近似处理次数,并根据产品数据手册拟合获取驱动电压对损耗的影响函数,从而对现有基于数据手册的损耗模型进行优化.在通态损耗模型中,将最大、最小典型温度下的损耗用电流的多项式进行拟合,利用线性插值的方法得到任意温度下的通态损耗,并考虑了驱动电压的影响.提出的损耗模型相比于现有基于数据手册的损耗模型,精度平均提高了9.21%,且使用工况更为广泛.
关键词:IGBT模块;动态电热耦合仿真;损耗模型;线性插值;多项式拟合
0引言
由于IGBT模块的电学特性与热学特性存在着较强的耦合关系,因此,作为能够真实反映IGBT模块工作特性的动态电热耦合仿真成为了国内外学者研究的热点[1].IGBT模块的动态电热耦合仿真运用到了损耗模型、传热模型和电网络模型.其中,损耗模型是模块电学特性与热学特性联接的枢纽,故该模型的准确建立是IGBT模块动态电热耦合仿真首先需要解决的关键问题[2].
IGBT的损耗模型可以划分为物理模型和行为模型两大类.其中,物理模型建模过程较为复杂、参数提取比较困难,且系统级仿真时间冗长,导致其在IGBT模块动态电热偶合仿真中的应用受到了一定限制[3].行为模型可以划分为基于曲线拟合理论的损耗模型和基于数学方法的损耗模型.
基于曲线拟合理论的损耗模型就其方法本身,存在着开关波形拟合误差,且未考虑温度对损耗的影响,难以适用于IGBT模块的动态电热耦合仿真[4-5].因此,国内外的研究重点侧重于基于数学方法的损耗模型.早期基于数学方法的损耗模型的损耗准确计算需要大量实验测试数据,且未考虑驱动电压对损耗的影响[6-7],因此,以文献[8]为代表提出的利用模块产品数据手册中的相关特性曲线建立损耗模型的方法,成为基于数学方法进行损耗建模的主流.然而,现有模型在通态损耗建模中采用了多次线性近似处理,且未考虑驱动电压对损耗的影响,仍然不能实现损耗的准确求解.本文从减少通态模型的线性近似处理次数,以及通过引入影响因子考虑驱动电压对损耗影响的角度出发,对现有基于数据手册的损耗模型进行优化,提高了损耗模型精度,且适用工况更广泛.
1IGBT模块动态耦合仿真及现有损耗模型
1.1IGBT模块动态电热耦合仿真计算流程
IGBT模块动态电热耦合仿真计算流程如图1所示.首先,模块损耗模型接收来自传热模型的瞬时温度,计算与温度的相关参数(通态电阻、不考虑驱动电压的通态损耗、不考虑驱动电阻及集射工作电压的开关损耗);接着电网络模型利用这些参数中的电气参数(通态电阻),计算出IGBT模块的电气运行参数(导通电流、导通压降);基于电气运行参数(导通电流、导通压降、驱动电压、驱动电阻)、温度相关损耗参数(不考虑驱动电压的通态损耗、不考虑驱动电阻及导通压降的开关损耗),采用合理的损耗模型计算得到模块的损耗,并将其传递给传热模型;传热模型将计算出的瞬时温度再次传递给模块损耗模型[4].

图1 IGBT模块动态电热耦合仿真计算流程
如此循环往复,使损耗模型和传热模型通过损耗和温度相互传递,实现了IGBT模块的动态电热耦合仿真,从而实时计算出IGBT模块的损耗和温度.
从图1可以看出,在IGBT模块动态电热耦合仿真计算中,损耗模型与传热模型、电网络模型之间相互联系紧密,其准确性直接影响到模块动态电热耦合仿真的精度.
1.2现有基于数据手册的损耗模型缺陷分析
IGBT模块在硬开关状态下的损耗分为IGBT损耗和续流二极管(FWD)损耗,其中IGBT损耗主要包括:通态损耗、开通损耗和关断损耗;FWD损耗主要包括:通态损耗和反向恢复损耗.
现有基于数据手册的IGBT通态损耗模型通常根据数据手册提供的VCE-IC输出特性曲线,将通态压降用集电极电流线性近似表示[9-12],见公式(1),该通态压降表达式中的通态电阻RT、阀值电压VCE0均与结温TTj相关,将其用结温线性近似表示,见公式(2)~(3),而后把通态损耗表示成通态压降、集电极电流和导通占空比乘积的形式,见公式(4).因此,从公式(1)~(3)可以看出,通态损耗模型在构建过程中进行了3次线性近似处理,且未考虑驱动电压对通态损耗的影响,只适合某个特定驱动电压下的IGBT通态损耗计算.
(1)
(2)
(3)
(4)
式中,RT_25和VT_25分别为IGBT在25℃下的通态电阻和阀值电压;δT为导通占空比;kRT和kVCE0分别为导通电阻和阀值压降的温度系数.
FWD通态损耗建模类似IGBT通态损耗建模,也进行了3次线性近似处理,只不过FWD不需要考虑驱动电压对通态损耗的影响.
2IGBT模块损耗模型的改进
针对于上述基于数据手册的损耗模型存在的线性近似处理次数过多,以及未考虑驱动电压影响的问题,提出采用以下思想对该模型进行优化.1)转换通态损耗的建模思路,减少IGBT、FWD通态损耗模型的线性近似处理次数,以此提高通态损耗模型的精度;2)在通态损耗模型中,根据产品数据手册拟合获取驱动电压对损耗的影响函数.
2.1IGBT通态损耗的改进
由于IGBT内部通态电阻和PN结电位的影响,处于导通状态下的IGBT会存在着一定的电压降VCE,与集电极电流IC共同作用产生通态损耗PTcon.影响IGBT通态损耗的主要因素有集电极电流IC、结温TTj和驱动电压VG[13-14].
从减少IGBT通态损耗模型线性近似处理次数的角度出发,首先将IGBT模块产品数据手册提供的最小典型温度TTmin和最大典型温度TTmax下的IC-VCE输出特性曲线,转化成相应的用3次函数多项式拟合的PTcon-IC特性曲线,如图2所示,分别得到式(5)、(6),式中系数可通过Matlab拟合工具箱拟合得到.
(5)
(6)
引入线性插值的方法,可得到任意温度下的IGBT通态损耗,如图3所示.

图2 PTcon-IC曲线拟合
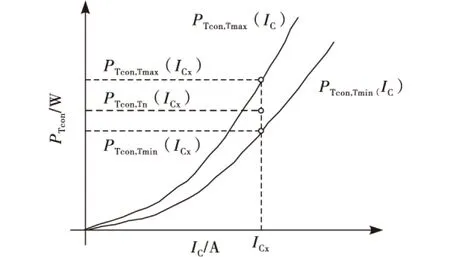
图3 任意温度下IGBT通态损耗的线性插值
为考虑驱动电压对IGBT通态损耗的影响,根据数据手册提供的多个典型驱动电压下的IC-VCE输出特性曲线,得到不同驱动电压下的通态损耗,并对其进行拟合,获取驱动电压对通态损耗的影响函数.综合计算准确性和复杂度,在IGBT通态损耗计算中引入影响因子VG/VGrated,如IGBT通态损耗表达式(7)所示.
综上所述,IGBT通态损耗的表达式为
(7)
式中,VGrated为IGBT额定驱动电压;δT为IGBT导通占空比;线性插值系数aT和bT分别为
(8)
(9)
从上述推导中可以看出,改进的通态损耗模型避免了传统IGBT通态损耗模型中公式(1)~(3)的3次线性近似处理,只在考虑温度对通态损耗的影响过程中进行了1次线性近似处理,见公式(7).
2.2FWD通态损耗
FWD为不可控器件,其通态损耗建模无需考虑驱动电压的影响.因此,影响FWD通态损耗的主要因素有工作电流IF、结温TDj[13-14],其他分析类似上述2.1节IGBT通态损耗分析.
FWD在最小典型温度TDmin和最大典型温度TDmax下的通态损耗PDcon与工作电流IF的函数拟合关系式分别如式(10)、(11)所示,式中系数可通过Matlab拟合工具箱拟合得到.
(10)
(11)
接着采用线性插值的方法得到任意温度下的FWD通态损耗,表达式为
(12)
式中,δD为FWD导通占空比;线性插值系数aD和bD分别为
(13)
(14)
3算例验证及误差分析
3.1算例验证
以两电平三相桥式SPWM逆变器为实例,进行IGBT模块的损耗分析计算,其结构和实验测试电路分别如图4~5所示.
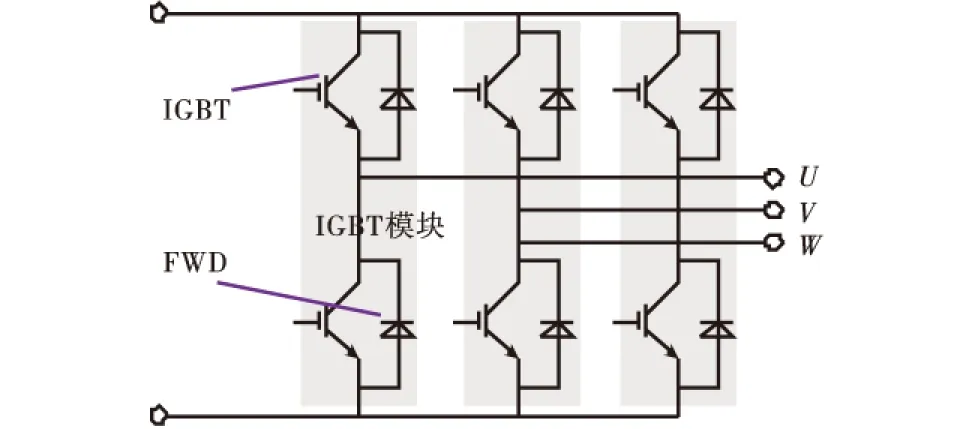
图4 两电平三相桥式SPWM逆变器电路结构

图5 两电平三相桥式SPWM逆变器实验电路

参数数值输入直流电压/V500功率因数0.85开关频率/Hz2500输出频率/Hz50分散电感/nH78环境温度/℃25IGBT模块型号2MBI75S-120
由于逆变器结构上的对称性,各相IGBT与FWD的电压、电流波形仅存在相位上的差异,因此只需对1个IGBT模块进行损耗分析,其他IGBT模块分析类似.在Matlab/Simulink中建立IGBT模块的电网络模型、损耗模型和等效Foster传热网络模型,对其进行电热耦合仿真,实时计算出IGBT模块的损耗.
IGBT和FWD在一个开关周期Ts内的导通占空比可分别表示为[15]:
(15)
(16)
式中,ω为角频率;φ为交流电压与电流基波分量之间的夹角;m为调制度.
IGBT模块损耗模型的参数见表2,等效Foster传热网络模型的参数见表3[12].

表2 2MBI75S-120型IGBT模块损耗模型参数

表3 2MBI75S-120型IGBT模块等效Foster传热网络模型参数
将损耗实验测量结果、改进的损耗模型计算结果、现有损耗模型计算结果进行对比,如图6所示.

图6 损耗结果对比
从图6的实验测量结果和仿真计算结果可以计算得出,改进的损耗模型的平均精度为89.19%,而现有损耗模型的平均精度为79.98%,精度平均提高了9.21%.
IGBT模块中的IGBT、FWD结温的仿真计算结果与实验测量结果的对比分别如图7~8所示.
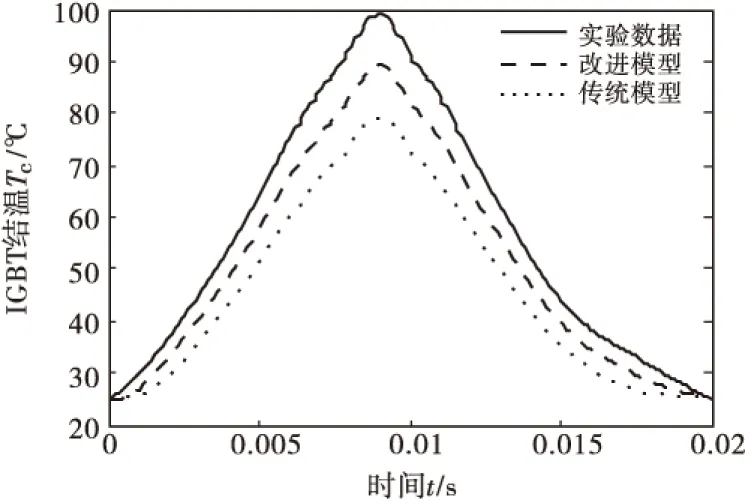
图7 IGBT结温结果对比
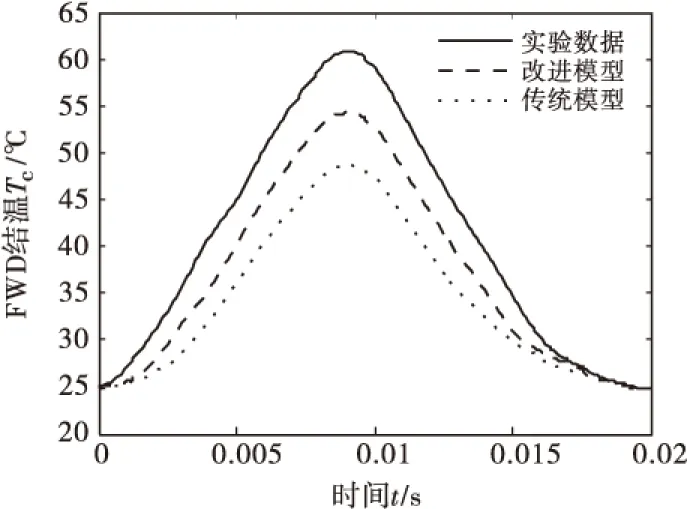
图8 FWD结温结果对比
从图7中可以得出,用改进的损耗模型计算出来的IGBT结温平均精度为88.57%,而用现有损耗模型计算出来的IGBT结温平均精度为79.64%,IGBT结温计算精度平均提高了8.93%;从图8可以得出,用改进的损耗模型计算出来的FWD结温平均精度为88.15%,而用现有损耗模型计算出来的FWD结温平均精度为79.26%,FWD结温计算精度平均提高了8.86%.
3.2误差分析
相比于现有基于数据手册的IGBT模块通态损耗模型,改进的IGBT模块通态损耗模型总共少了4次线性近似处理(IGBT、FWD各少2次),使损耗仿真计算精度提高了9.21%,同时加入拟合公式考虑了驱动电压对IGBT通态损耗的影响.该改进的损耗模型用于IGBT模块动态电热耦合仿真时,由于损耗计算的精度有了较大提升,IGBT和FWD结温的计算精度平均分别提高了8.93%和8.86%.
从图6~8的损耗结果对比可以看出,改进的损耗模型和现有损耗模型的计算结果均低于实验测量结果,这是由于在建模过程均未考虑到IGBT模块中热源之间的热耦合作用等原因造成的.
4结论
1)基于减少通态损耗模型线性近似处理次数的思想,转换建模思路,使改进的损耗模型相比于现有损耗模型,少了4次线性近似处理,精度平均提高了9.21%.
2)改进的损耗模型相比于现有损耗模型,根据产品数据手册拟合获取驱动电压对损耗的影响因子,考虑了驱动电压对IGBT通态损耗的影响,适用于不同驱动电压工况下的IGBT模块损耗求解.
参考文献:
[1]Zhou Z,Kanniche M S,Butcup S G,et al. High-speed Electro-thermal Simulation Model of Inverter Power Modules for Hybrid Vehicles[J]. IET Electric Power Applications,2011,5(8):636-643.
[2]Hefner A R. Analytical Modeling of Device-circuit Interactions for the Power Insulated Gate Bipolar Transistor (IGBT)[J]. IEEE Transactions on Industry Applications,1990,26:995-1005.
[3]Hefner A R. A Dynamic Electro-thermal Model for the IGBT[J]. IEEE Transactions on Industry Applications,1994,30(2):394-405.
[4]Rajapakse A D,Gole A M,Wilson P L. Electromagnetic Transient Simulation Models for Accurate Representation of Switching Losses and Thermal Performance in Power Electronic Systems[J]. IEEE Transactions on Power Delivery,2005,20(1):319-327.
[5]潘武略,徐政,张静,等. 电压源换流器型直流输电换流器损耗分析[J].中国电机工程学报,2008,28(21):7-14.
[6]Blaabjerg F,Jaeger U,Munk-Nielsen S,et al. Power Losses in PWM-VSI Inverter Using NPT or PT IGBT Devices[J]. lEEE Transactions on power Elecdronics,1995,10(3):358-367.
[7]许德伟,朱东起,黄立培,等.电力半导体器件和装置的功率损耗研究[J].清华大学学报,2000,40(3):5-8.
[8]Rcichl J V. Inverter Dynamic Electro-thermal Simulation with Experiment Verification[D]. Blacksburg,Virginia Polytechnic institute and State University,2005.
[9]杜雄,李高显,吴军科,等.一种用于风电变流器可靠性评估的结温数值计算方法[J].中国电机工程学报,2015,35(11):2813-2821.
[10] 徐铭伟,周锥维,杜雄,等.三相逆变器中绝缘栅双极型晶体管模块结温仿真评估[J].重庆大学学报,2014,37(2):37-45.
[11] 屠卿瑞,徐政.基于结温反馈方法的模块化多电平换流器型高压直流输电阀损耗评估[J].高电压技术,2012,38(6):1506-1512.
[12] 徐铭伟.绝缘栅双极型晶体管结温仿真模型及其应用研究[D].重庆:重庆大学,2012.
[13] J Hoon Lee,Bo H. Cho. Large Time-scale Electro-thermal Simulation for Loss and Thermal Management of Power MOSFET[C]. Power Electronics Specialist Conference, 2003(1):112-117.
[14] Rcichl J V. Inverter Dynamic Electro-thermal Simulation with Experiment Verification[D]. Blacksburg,Virginia Polytechnic institute and State University,2005.
[15] 秦星.风电变流器IGBT模块结温计算及功率循环能力评估[D].重庆:重庆大学,2014.
[责任编辑张莉]
DOI:10.13393/j.cnki.issn.1672-948X.2016.03.015
收稿日期:2016-02-01
基金项目:新能源电力系统国家重点实验室开放基金(LAPS14016);2015年三峡大学研究生科研创新基金(2015CX061)
通信作者:刘任(1990-),男,硕士研究生,研究方向为输变电系统电磁环境.E-mail:505129963@qq.com
中图分类号:TM464:TM411:TN303
文献标识码:A
文章编号:1672-948X(2016)03-0064-05
Loss Model Optimization for Dynamic Electro-thermal Simulation of IGBT Module
Liu RenTang BoSun RuiWu ZhuoJiang Haotian
(College of Electrical Engineering & Renewable Energy, China Three Gorges Univ., Yichang 443002, China)
AbstractThe key problem of the simulation analysis of dynamic electro-thermal coupling simulation of insulated gate bipolar transistor (IGBT) module is the accurate establishment of loss model. The existing loss model based on datasheet is optimized from reducing the linear approximation of the state loss model and obtaining the influence function of driving voltage on loss according to the product datasheet. In the conduction loss model, the loss at maximum and minimum typical temperature are fitted by the polynomial of current, then the conduction state loss at any temperature is obtained by using the linear interpolation method; and the influence of the driving voltage is considered. Compared to the existing loss model based on datasheet, the proposed model has a higher accuracy of 9.21%; and the use of the operating conditions is more extensive.
KeywordsIGBT module;dynamic electro-thermal simulation;loss model;linear interpolation;polynomial fitting

