基于流形思想的有限条法初步研究

祁勇峰　苏海东　颉志强　龚亚琦

(1. 长江科学院 水利部水工程安全与病害防治工程技术研究中心； 2. 长江科学院 材料与结构研究所， 武汉　430010)



基于流形思想的有限条法初步研究

祁勇峰1，2苏海东1，2颉志强1，2龚亚琦1，2

(1. 长江科学院 水利部水工程安全与病害防治工程技术研究中心； 2. 长江科学院 材料与结构研究所， 武汉430010)

摘要：针对梁、板等结构，有限条法是一种高效的计算方法，但一直以来只能分析规则形状的结构，从而限制了其应用范围．应用流形法数学网格与物理网格分离的特性，提出基于流形思想的有限条法，将以往只能用于规则形状的有限条法扩展到分析复杂形状．在计算域采用长条形的矩形数学网格覆盖，在长条方向通过结点的强制约束实现条向的高阶多项式级数分布，而垂直于条向为常规的有限元插值方式，并推导相应计算公式．最后，应用深梁、重力坝算例验证了此方法的有效性．

关键词：有限条法；流形；复杂形状

有限条法[1]在20世纪60年代末由张佑启(YK.Cheung)博士创立．该方法将连续体离散为条元，在不同方向采用不同的离散方式，类似于求解微分方程时的分离变量法．其中比较简单的一种离散方式是：在一个方向上采用有限元低阶多项式，在其他方向采用连续可微光滑的级数或样条函数．有限条法是解决板、壳、梁问题的半解析有限元法，除了位移函数的选择有所不同外，其它方面和有限单元法完全类似．基于上述特点，有限条法作为一种结构分析的有效方法在弹性小变形领域得到了广泛的应用．国内外关于有限条法的研究也比较深入，但大多只是用来研究较为规则的形状(如矩形板、梁、壳等)[2-4]，仅少数文献采用样条有限条法分析其他形状(通过映射到一个矩形区域)的板问题，其应用范围受到了一定限制．

留美学者石根华博士提出了一种全新的数值分析方法—数值流形方法[5](以下简称流形法)．流形法采用两套网格，即物理网格和数学网格，两套网格相互独立，数学网格用来定义插值域，物理网格用来定义结构边界和积分区域，物理网格与数学网格的交集，称为流形元，可具有任意的形状．流形法的一个独特之处在于，在数学网格保持不变的前提下，可通过覆盖函数升阶或在覆盖上构造特殊的覆盖函数来提高插值域内的求解精度，自适应相对灵活．为此，利用流形法数学网格与物理网格分离的特性以及上述优势，并结合石根华博士提出基于流形的有限条法思想，可将有限条法推广到任意形状，本文将对这种全新的思想进行初步研究．

1有限条法的力学模型

有限条法可看作是有限元的一种特殊形式，是一种半解析法，适应于比较规则的结构．有限条法也需将连续体离散化，但不能像有限元那样可沿任意方向离散，而只能沿某一方向离散．如图1所示矩形深梁，用有限条分析(矩形长条单元)的网格划分如图1所示，结构沿x方向等分成若干条带．

图1　有限条的离散方式

2基于流形思想的有限条法

如图2(a)所示的条状网格，如果数学网格与物理网格一致，在水平向采用有限元的离散方式，而在垂直向使用强制约束信息(括号中的数据)，使之采用同一个覆盖函数(比如通常有限条中为满足边界条件而采用的三角类级数)，则流形法就成为通常的有限条法．如图2(b)所示，不规则形状的结构(如重力坝)也用条状的数学网格覆盖．由于流形法具有物理网格和数学网格分离的特性，当采用多项式覆盖函数时，单纯形积分可以保证不规则形状积分的准确性，因此流形法可以将有限条法推广到任意形状．

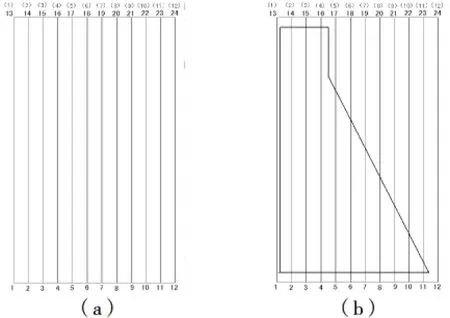
图2　条状覆盖系统

笔者在文献[6]中实现了在流形法网格内的结点采用不同的覆盖函数，其矩形网格的位移函数表达式如下

(1)

式中，Wi(x，y)为权函数，uij，vij为覆盖函数的系数；m(i)为定义在结点i上的多项式覆盖函数项数，根据不同的结点i，m(i)取不同的项数；tj(x，y)是多项式基底，一般采用如1，x，y等的全局覆盖函数形式，表示为xn-kyk(其中n=0～p，p为最高阶数，k=0～n)．

在式(1)基础上，进一步改进流形元的计算公式，使不同方向可以采用不同的多项式函数，即局部多项式覆盖函数xn-kyk中取n=k，从而实现x向为0阶的重叠覆盖流形元，y向为高阶多项式覆盖函数，在结线上为

(2)

式中，p为最高阶数，结线j1和j2之间的条形内部用权函数连接

(3)

其中wj1、wj2为一维权函数．

在y向采用多项式级数，一般不能保证满足本质边界条件，因此本文仍然采用一般流形法的罚函数方式引入边界条件．

基于流形思想的有限条法具有独特的覆盖形式和表示方式，本文应采用一套新的计算公式，考虑到文献[6]中基于部分重叠流形法思想，已推导出一套成熟的单元矩阵分析公式，其公式可用于本文，只是位移覆盖函数表达式(式2、3)不同而已．因此，本文相关单元矩阵公式从略．

3算例分析

3.1深梁受分布荷载作用算例

首先计算规则的有限条．如图3所示的深梁，几何尺寸为1 m×1 m，两端固定约束，顶部作用有P=1 000 kN/m的分布荷载．弹性模量E=0.3 GPa，泊松比μ=0.1．图4为数学网格，划分8个矩形条(数学网格)，图5为流形元网格，图6的稠密有限元网格作为对比，共计256个有限单元．分别采用3阶、4阶、5阶覆盖函数的流形法进行计算．流形法与有限元法的计算结果如图7～8所示．

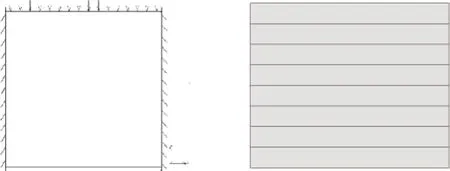
图3　深梁示意图　　　　　图4　数学网格

图5　流形元　　　　　　图6　有限单元

图7　流形法与有限元法的各条中心点y向位移比较

图8　流形法与有限元法的各条中心点y向正应力比较

由图可知，3阶流形法与有限元法的计算结果已比较接近，4阶、5阶流形法与有限元的计算结果基本吻合．这表明基于流形思想的有限条法可以很好地计算通常的规则形状的有限条．

3.2重力坝受水压作用算例

如图9所示的重力坝，坝高100 m，坝底长为60 m，坝顶宽度20 m，库水深80 m．坝体弹性模量为30 GPa，泊松比为0.167．其中x向为顺水流向，y向为竖直向．计算上游面承受库水压力情况下的应力和变形．采用矩形条的数学网格(如图10所示)计算坝体变形，采用稠密网格的有限元计算结果(如图11所示)作为对比，划分1 080个4结点等参元．

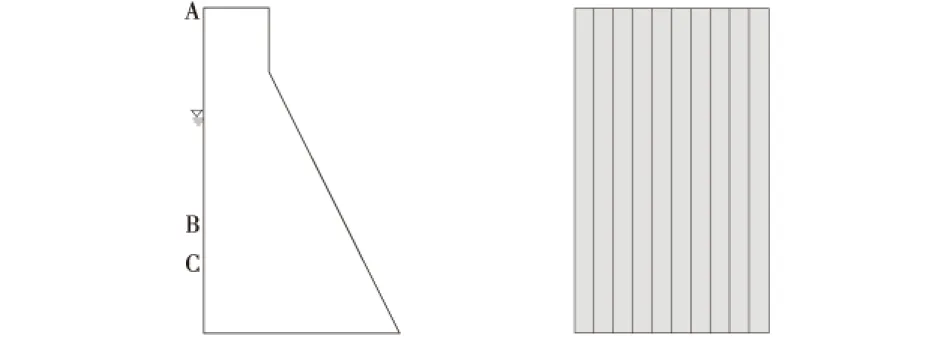
图9　深梁示意图　　图10　数学网格

图11　有限元网格　　　图12　流形元

由图13～15计算成果对比可知，3阶流形法与有限元法的位移计算结果已经比较接近．而上游面的应力在采用5阶流形法时，靠近坝踵附近部位由于约束的影响难以获得较好的结果．因此，将覆盖升阶至7阶甚至9阶后，应力有了很大改善，与有限元解很接近．以上重力坝算例说明，基于流形思想的有限条法也可以较好地计算非规则形状的结构．这样就将通常只能计算规则形状的有限条法扩展为计算一般的形状．对于某些计算结果不理想的区域，通过提高该覆盖中的多项式阶数也可以提高计算精度．

图13　上游面不同高程特征点x向位移

图14　特征点x向应力结果对比

图15　特征点y向应力结果对比

4结论与展望

为了与以往的常规有限条保持一定的相似性，本文在垂直于条形的方向采用了有限元的插值方式，即完全重叠的0阶多项式覆盖，而垂直于条向为常规的有限元插值方式，形成了基于流形思想的有限条分析方法，将以往只能用于规则形状的有限条法扩展到分析复杂形状，并应用深梁、重力坝算例验证了这种方法的有效性．进一步可以在条形方向采用相对高阶多项式覆盖函数，从而提高此方向的计算精度或相应地减少条的数目，也可尝试其它类型的级数，如有限条法经常采用的三角类级数，但应注意数值积分的精度问题．

在此基础上，可以研究三维有限条，而在另一方向上采用低阶插值方式．针对梁、板等结构，有限条法是一种高效的计算方法，但一直以来只能分析规则形状，从而限制了其应用范围，研究趋于停滞．本文将其扩展到分析不规则形状，有望使这种沉寂多年的高效数值方法焕发新的活力．

参考文献：

[1](英)张佑启．结构分析的有限条法[M]．谢秀松，等译．北京：人民交通出版社，1985．

[2]程远胜，张佑启，区达光．有限条法分析板在移动车载作用下的动响应[J]．应用数学与力学，2002，23(5)：453-458．

[3]冯侃，徐吉峰．基于升阶谱有限条法的复合材料壁板结构稳定性分析[J]．固体力学学报，2015，36(4)：346-352．

[4]Lezin S. Minsili， 夏禾，等．混凝土板梁的有限条法简化分析(英文)[J]．北京交通大学学报，2009，33(6)：61-69．

[5]石根华．数值流形方法与非连续变形分析[M]．裴觉民，译．北京：清华大学出版社，1997．

[6]祁勇峰，苏海东．部分重叠覆盖的流形法研究报告[R]．武汉：长江科学院，2012．

[责任编辑王康平]

DOI：10.13393/j.cnki.issn.1672-948X.2016.03.004

收稿日期：2016-01-13

基金项目：国家自然科学基金青年基金项目(51409012)；中央级公益性科研院所基本科研业务费项目(CKSF2014054/CL、CKSF2016022/CL)

通信作者：祁勇峰(1978-)，男，高级工程师，主要从事水工结构研究．E-mail：qiyf@mail.crsri.cn

中图分类号：TV64

文献标识码：A

文章编号：1672-948X(2016)03-0015-04

Preliminary Study of Finite Strip Method Based on Manifold

Qi Yongfeng1,2Su Haidong1,2Jie Zhiqiang1,2Gong Yaqi1,2

(1. Research Center on Water Engineering Safety & Disaster Prevention of Mimistry of Water Resources，Yangtze River Scientific Research Institute，Wuhan 430010，China；2．Material & Engineering Structure Department，Yangtze River Scientific Research Institute，Wuhan 430010，China)

AbstractThe finite strip method is an efficient calculation method for beams or plates and other structures; but it is only used for analyzing regular shape, so as to limit its application scope. Based on separation characteristics of mathematical meshes and physical meshes of numerical manifold method, a finite strip method based on the manifold is proposed, which can be used for analyzing complex shape but not limited to regular shape.` In Calculation domain, rectangle mathematical cover of strip shape is adopted, in which the high order polynomial is carried out by forced node constraints in strip direction and the interpolation function for conventional finite element method in vertical direction; and then a corresponding formula is also derived. Finally, the validity of new method is demonstrated by case studies of deep beams and gravity dam．

Keywordsfinite strip method；manifold；complex shape