基于MIV-改进RBF神经网络的大坝变形监测模型
宁昕扬 刘晓青
(河海大学 水利水电学院, 南京 210098)
基于MIV-改进RBF神经网络的大坝变形监测模型
宁昕扬刘晓青
(河海大学 水利水电学院, 南京210098)
摘要:针对常规径向基函数(RBF)神经网络模型无法选择显著预报因子和易陷入局部最优解的问题,建立一种融合平均影响值(MIV)、改进果蝇算法(FOA)和RBF神经网络的大坝变形监测模型.通过引入MIV对水压、温度、时效三类预报因子进行筛选,并利用改进FOA算法获得RBF神经网络模型中最佳的spread值,以提高模型的稳定性和预报精度.为验证模型的有效性,以某混凝土重力坝位移监测数据为例,分别建立多元线性回归模型、常规RBF模型、MIV-RBF模型和MIV-改进RBF模型.研究结果表明MIV-改进RBF神经网络大坝变形监测模型预测稳定、精度高,预报效果好.
关键词:MIV算法;变量筛选;改进RBF神经网络;大坝变形监测模型
大坝变形监测预报研究对大坝安全运行具有重要意义.传统的大坝变形监控模型主要采用回归分析法对位移观测数据进行处理,所建立的模型是线性的[1].实际大坝变形还受到地质、地形、筑坝材料等因素的影响,具有很强的非线性.因而,回归模型预报结果常出现预报精度低和拟合效果欠佳的情况.近年来兴起的人工神经网络技术因其无需考虑所引入变量具体的物理意义,而更加考究数据量之间的关系,在非线性和不确定性问题的处理中得到了广泛地应用[2].
径向基函数(RBF)神经网络较BP神经网络具有结构简单、逼近速度快和更强非线性处理能力[3]的特点,一些学者已将其广泛地应用于结构安全监测的非线性问题中.张晓春[2]建立了坝段挠度预测的径向基神经网络模型;黄潇霏[4]利用蚁群聚类算法构建了径向基神经网络隐层基函数模型;吕蓓蓓[5]引入POS算法对传统径向基函数进行改进,拟合效果较传统RBF有明显提升.
常规的RBF神经网络模型往往忽略对预报因子的优化筛选,不相关因子的引入会直接导致预报结果不稳定或者结果难以解释;网络泛化能力不强极易使RBF网络陷入局部最优解.平均影响值(MIV)是评价神经网络变量相关性最好的指标之一;同时文献[6-7]研究表明FOA-RBF方法的稳定性及泛化能力优于PSO-RBF和GA-RBF,并且改进的FOA在寻优方面效果更佳.本文通过引入平均影响值(mean impact value, MIV)进行预报因子的筛选,并利用改进的果蝇(FOA)算法优化RBF神经网络中的spread值,以某重力坝变形监测数据为例,建立基于MIV-改进的RBF神经网络重力坝变形预测模型,并验证其有效性.
1MIV算法
平均影响值法(MIV)由Dombi等人提出,可用于衡量输入神经元对输出神经元影响程度.具体计算过程如下:对原样本量M进行神经网络训练;将训练后样本M作为输入神经元的变量值相对其原值上下变动10%,形成新的输入神经元样本(M1和M2);将M1和M2作为新的样本量,利用已建成的神经网络进行预测,预测结果为N1和N2;计算N1和N2的差值,并根据输入神经元数量进行平均,得到该输入神经元的平均影响值MIV(MIV的正负代表相关方向,绝对值代表影响大小).MIV越大,则其影响越大[8].
由以上过程可知,MIV算法实现简便,同时因其通过神经网络进行训练,故MIV算法适用于复杂非线性问题中预报因子的筛选.
2改进的RBF神经网络模型
2.1RBF神经网络模型
RBF神经网络模型,由输入层、隐藏层和输出层组成,适用于解决各类非线性问题.该模型的基本原理是:以RBF作为隐藏单元的“基”构建隐藏层空间,利用隐藏层将低维的输入量变换到高维空间并分解,模型的结构拓扑如图1所示[3].

图1 RBF网络拓扑结构示意图
RBF神经网络的创建可通过Matlab中的newrbe函数生成,其格式为

(1)
式中,P为输入向量;T为输出向量;spread为扩展速度.
其中spread的选择直接影响RBF神经网络预报性能.spread越大,RBF神经网络的拟合越平滑.但spread过大,将导致RBF神经网络中的神经元过度交叠;spread过小,将导致神经元扩展速度不能包含所有输入区域[6].
2.2改进FOA-RBF神经网络
果蝇算法(FOA)是一种基于果蝇觅食行为的智能优化算法[9].传统果蝇算法在寻优过程中,由于搜索半径r是人为设定,不合理的搜索半径,极易导致算法陷入局部极值或者错过最优解.因此,本文采用改进的果蝇算法,以调整不同迭代次数(奇数偶数次)对应搜索半径r的大小[7].
当迭代次数为奇数时,令算法对全局范围内搜索,即设置搜索半径r为足够大的值;当迭代次数为偶数时,令算法在奇数次迭代搜索到的最优值附近寻优,即设置搜索半径为足够小的值.通过如此循环,确保了该算法找到全局最优解.r值的计算方法如下:
(2)
(3)

(4)
式中,i为当前迭代次数,△Smellbest为每次优化幅值,Maxgen为最大迭代次数.
由于spread是影响RBF神经网络的关键因素,本文采用上述改进的FOA算法对其进行迭代寻优.总体思路是将spread值作为改进FOA算法的味道浓度,预测误差的绝对值作为味道浓度判定函数,具体过程如下[6]:
步骤1:设置果蝇群体初始参数.
随机初始位置(X0,Y0),种群规模sizepop=40,迭代次数Maxgen=20.
步骤2:给定果蝇个体通过嗅觉搜索食物的随机方向γ(其中γ为[0,1]的随机数)和半径r(见式(2)~(4)).即得果蝇经过第i次迭代后的位置为(Xi,Yi).(其中Xi=X0+r*(γ-0.5),Yi=Y0+r*(γ-0.5))
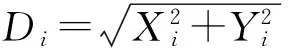
步骤4:确定味道浓度判定值Si,即为spread.(Si=1/Di,spread=Si)
步骤5:将spread值代入newrbe函数.
net=newrbe(P,T,spread)%训练数据,建立RBF网络
a=sim(net,P_test)%RBF网络预测
err=P_test-a%预测误差
Functioni=(err)2%预测误差平方
步骤6:对比第i个果蝇所经过位置的味道浓度判定值.
步骤7:保留最佳判定值和位置并进行迭代寻优,直到迭代终止.
3基于MIV-改进RBF神经网络大坝变形监测模型
3.1工程概况
某水电站大坝枢纽工程主要建筑物由高碾压混凝土重力坝、坝顶5孔泄水闸、引水建筑物、发电厂房和开关站等组成.其中坝顶宽度6.0m,坝顶高程153.00m,坝底高程41.00m,最大坝高112.00m.坝体变形监测通过设置的引张线、倒垂线、静力水准仪等完成并将测得的数据进行统计,分析不同坝段、不同高程坝体的顺河向位移、横河向位移以及垂直向位
移的时空变化规律.
3.2变形监测模型
混凝土重力坝任一点变形位移δ是在水压力、扬压力、温度等荷载作用下产生的,故按照其成因可分为水压分量δH、温度分量δT和时效分量δθ[1],即:
(5)
按照式(5)的分量,分别取水压为H、H2、H3,温度为T1、T2、T3、T4,时效为θ、ln(θ).
鉴于该大坝属于蓄水初期,坝体的开裂、失稳多与坝体变形有关,因此变形监测是混凝土重力坝的重要指标,而在变形监测中,顺河向的水平位移最为重要[10].选取2012年1月10日-2013年7月31日的坝顶153m高程处1号坝段顺河向位移及相关影响因子作为样本量,进行预测分析.
3.3MIV算法筛选预报因子
首先对样本数据做预处理,将所有量统一到[0.1,0.599],其中输入向量为H、H2、H3、T1、T2、T3、T4、θ、ln(θ),输出向量为顺河向位移δ,并按式(6)转换,以避免样本大小及奇异样本数据的影响.
(6)
利用总样本数据和改进的RBF神经网络创建一个神经网络成最优的RBF神经网络[8]后(其中迭代20次的最佳适应度值为0.011 8),计算每个输入神经元的MIV值.具体计算流程见图2,MIV计算结果见表1.由表1可得:H3、T4、H2、ln(θ)对顺河向位移影响程度较大,故选择上述4个因子作为RBF网络的输入变量.
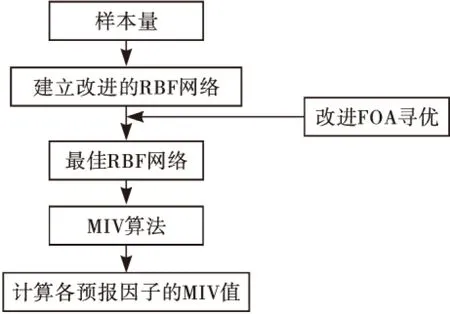
图2 MIV算法筛选流程图

影响因子HH2H3θln(θ)T1T2T3T4MIV绝对值0.00580.3070.370.00450.1420.00740.3430.00780.0046排序731946258
3.4构建MIV-改进RBF网络
将MIV算法筛选后的因子和位移重组成新的样本量,并将该样本分为训练组和预测组两部分,其中训练组271组,预测组为25组,进行MIV-改进RBF网络预测.
具体实现步骤如下:
步骤1:依据MIV筛选因子构建RBF网络,确定输入变量训练组中的H3、T4、H2、ln(θ),输出变量为顺河向位移δ.
步骤2:按照改进FOA算法迭代优化RBF以获得最佳的spread值,即为最佳RBF网络.
步骤3:提取预测组中的的H3、T4、H2、ln(θ)顺河向位移影响较大,并将其作为步骤2中最佳RBF网络的输入样本组P_test*,进行顺河向位移δ*的预测分析,δ*=sim(net,P_test*).
步骤4:将所得顺河向位移预测值δ*做反归一化处理.
3.5计算结果分析
为验证MIV-RBF神经网络大坝变形监测模型的有效性,本文另外利用相同样本量中的训练组分别建立多元线性回归模型、常规RBF网络模型和MIV-RBF网络模型,并对预测组进行预测分析.其中多元线性回归方程见式(9),常规RBF网络中的spread值设为1(默认值),不同模型预测值过程线见图3,预测值及误差结果见表2.
δ=8.170 6-0.008 948 4*H-0.010 854H2+
0.000 663 28H3+0.031 661T1-0.265 73T2-
0.033 723T3-0.023 756T4-
(7)
式中,H为水位;T1、T2、T3、T4为温度;θ、ln(θ)为时效分量.

图3 不同模型预测趋势图

时间实测值多元线性回归模型预测值 相对误差/%常规RBF神经网络模型预测值 相对误差/%MIV-RBF神经网络模型预测值 相对误差/%MIV-改进RBF神经网络模型预测值 相对误差/%20120219-0.25-0.485-93.88-0.263-5.38-0.226-9.62-0.245-1.9820120229-0.26-0.560-115.22-0.236-9.43-0.269-3.54-0.243-6.7120120320-0.39-0.542-38.88-0.461-18.14-0.080-79.43-0.380-2.5320120515-1.16-1.096-5.51-1.000-13.80-1.432-23.41-1.152-0.6920120614-0.82-1.221-48.87-0.738-10.06-0.947-15.47-0.859-4.8020120624-0.91-1.152-26.60-0.594-34.76-0.815-10.39-0.869-4.4620120704-0.97-1.101-13.48-1.055-8.80-0.958-1.26-0.888-8.4320120714-0.90-1.147-27.49-0.884-1.78-0.818-9.06-0.843-6.2920120724-0.81-1.054-30.13-0.851-5.12-0.817-0.82-0.777-4.0220120803-0.81-1.257-55.20-2.466-204.50-0.793-2.15-0.844-4.2220120813-0.73-0.954-30.69-0.814-11.50-0.768-5.17-0.711-2.5820120823-0.83-1.115-34.32-0.799-3.72-0.804-3.10-0.789-4.8820120902-0.78-1.192-52.80-0.628-19.47-0.793-1.63-0.787-0.8820120912-0.71-1.037-45.99-0.714-0.56-0.673-5.21-0.715-0.7020120922-0.63-0.974-54.52-0.753-19.50-0.605-3.93-0.679-7.7820121002-0.65-0.949-45.98-0.670-3.05-0.665-2.28-0.649-0.2220121012-0.65-0.946-45.52-0.657-1.05-0.660-1.49-0.633-2.6820121022-0.58-0.970-67.26-0.639-10.24-0.594-2.36-0.630-8.6220121101-0.62-1.046-68.68-0.351-43.36-0.599-3.35-0.644-3.8020121112-0.63-1.097-74.09-0.580-7.97-0.626-0.60-0.662-5.1320121127-0.64-1.015-58.64-0.850-32.83-0.636-0.55-0.659-2.9820130205-0.60-1.089-81.50-2.381-296.87-0.627-4.48-0.620-3.3520130416-0.71-0.953-34.21-0.800-12.68-0.690-2.76-0.662-6.7120130625-0.82-1.339-63.22-0.600-26.84-0.508-38.07-0.786-4.1120130725-0.80-1.149-43.62-0.468-41.55-0.803-0.38-0.840-4.95相对误差平均值/%-50.25-33.72-9.22-4.14均方差0.3350.5060.1110.035
由图2可知,常规RBF模型偏差较大;多元线性回归模型预测趋势符合,但整体存在较大偏差;MIV-RBF模型和MIV-改进RBF模型较其它模型,预测趋势吻合,预测结果稳定,其中MIV-改进RBF模型拟合程度高,预测结果更好.
同时由表2可见,多元线性回归模型、常规RBF网络模型、MIV-RBF网络模型和MIV-改进RBF网络模型的相对误差平均值分别为:-50.25%、-33.72%、-9.22%和-4.14%;均方差分别为0.335、0.506、0.111和0.035.由此可见,常规RBF网络模型经过MIV筛选和改进后,预测精度提高明显,且误差较小,可用于变形预测分析.
4结论
大坝长期变形监测预报中,预报因子的筛选和监测模型的构建是关键.本文通过MIV算法筛选显著因子,以避免常规RBF模型预测出现不稳定或难以解释的情况;同时采用改进果蝇算法优化spread值,构建了最佳的RBF网络.工程实例计算结果表明,MIV-改进RBF神经网络相比于常规RBF网络预测稳定,精度高,在大坝变形监测中预报效果好.
参考文献:
[1]水工建筑物安全监控理论及其应用[M].南京:河海大学出版社,1990.
[2]张晓春,徐晖,邓念武,等.径向基函数神经网络在大坝安全监测数据处理中的应用[J].武汉大学学报:工学版,2003,36(2):33-36.
[3]曹欣荣,楼章华,孙宏巍.基于RBF神经网络的水闸垂直位移时间序列预测模型[J].三峡大学学报:自然科学版,2010,32(5):17-19.
[4]黄潇霏,顾昊.大坝变形蚁群聚类径向基函数神经网络安全监控预测模型[J].三峡大学学报:自然科学版,2014,36(6):33-36.
[5]吕蓓蓓,杨远斐.PSO-RBF在大坝变形监测中的应用[J].水电能源科学,2012,30(8):77-79.
[6]徐国宾,韩文文,王海军,等.水电站泄流诱发厂房结构振动响应预测[J].天津大学学报:自然科学与工程技术版,2015,48(3):196-202.
[7]李栋,张文宇.基于ELM和FOA的股票价格预测[J].计算机工程与应用,2014,18:14-18,32.
[8]徐富强,刘相国.基于优化的RBF神经网络的变量筛选方法[J].计算机系统应用,2012(3):206-208.
[9]PAN W T. A New Fruit Fly Optimization Algorithm:Taking the Financial Distress Model as An Example[J]. Knowledge-Based System,2012,26(1):69-74.
[10] 魏德荣.大坝安全监控指标的制定[J].大坝与安全,2003(6):24-28.
[责任编辑王康平]
DOI:10.13393/j.cnki.issn.1672-948X.2016.03.001
收稿日期:2016-01-20
基金项目:国家自然科学基金(51279050);土石坝长效安全运行重大关键技术研究(201501033)
通信作者:宁昕扬(1991-),男,硕士研究生,主要从事水工结构方面研究.E-mail:ninxiny@163.com
中图分类号:TV698
文献标识码:A
文章编号:1672-948X(2016)03-0001-05
Deformation Monitoring Model of Dam Based on MIV-Improved RBF Neural Network
Ning XinyangLiu Xiaoqing
(College of Water Conservancy & Hydropower Engineering, Hohai Univ., Nanjing 210098, China)
AbstractFor the fact that the standard radial basis function(RBF) neural network can't select the significant factors and is easy to jump into local optimum, a fusion of the mean impact value(MIV), improved fruit flies algorithm (FOA) and monitoring model of RBF neural network is established. Firstly, to select three kinds of forecast factor, that is, water pressure, temperature and prescription, the MIV is introduced. Then the FOA is used for searching the optimal spread value of RBF neural network model. By these two approaches, the stability and forecast precision of the model is improved. To verify the validity of the model, taking the displacement monitoring data of a concrete gravity dam for example, multiple linear regression model, the standard RBF model, the MIV-RBF model and MIV-improved RBF model are built respectively. The results show that the MIV-improved RBF neural network has great generalization ability, stable prediction and high precision. Meanwhile, the results of this monitor model of dam deformation prediction is remarkable and the model can be applied to practical engineering analysis of the deformation monitoring and early warning.
Keywordsmean impact value(MIV);variable selection;improved radial basis function(RBF) neural network;deformation monitoring model of dam

