基于滑模观测器的永磁同步电机无位置传感器控制*

张曲遥，　高艳霞，　陈　静，　宋文祥

(上海大学 机电工程与自动化学院，上海　200072)



基于滑模观测器的永磁同步电机无位置传感器控制*

张曲遥，高艳霞，陈静，宋文祥

(上海大学 机电工程与自动化学院，上海200072)

摘要：研究了一种基于滑模观测器的永磁同步电机无位置传感器控制方案。通过深入分析永磁同步电机(PMSM)的数学模型,提出用滑动模态观测器(SMO)对无位置传感器PMSM转速实现估算。由于引入低通滤波器易引起相位延迟，因此构建一个锁相环将观测的转子位置角和反电动势结合起来，以得到比较准确的转速。锁相环中的电机转速信息是由信号通过比例积分环节后得到的。仿真结果验证了控制方案的有效性和可行性。

关键词：永磁同步电动机； 无位置传感器控制； 滑动模态观测器； 锁相环

0引言

与其他种类的电机相比，永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)具有很多优点，如运转期间电磁转矩纹波系数小、转矩惯性比大、能量密度大、快速的动态响应能力、较强的过载能力等，近年来在航天、新能源交通、工厂自动化控制等领域获得了大量的应用。为了实现PMSM精准、快速、超调量小的控制，就要掌握电机转子位置等相关信息。传统获取转子位置是通过机械式位置传感器来实现的。机械式传感器的存在使系统变得复杂，提高了系统的安装维护成本，严重限制了永磁电机的推广使用。为避免机械传感器给使用永磁电机带来的诸多不便，无位置传感器控制技术自然成为了研究电机控制领域中的一个热点问题。

为实现PMSM的无位置传感器控制，行业内许多专家学者做了大量的工作，总结出了具体可行的实施方案。其中主要包括： (1) 状态观测器[3-4]法，直接或间接地从电机反电动势中提取电机转子位置信息，适用于内埋式和表贴式电机。该方法虽然具有较快的动态响应速度，但在电机低速尤其是零速运行时不能准确估测转子位置，故目前只适合于电机中高速运行的场合；(2) 利用电机的空间凸极效应，适合于较宽速度范围，且低速时估算结果偏差不大，但存在较大的高频噪声难以消除，因此只适合于内埋式永磁电机。其中研究者们对观测器法关注最多，传统的滑动模态观测器也是其中的一种。但是传统的滑模观测器方法是先进行观测估算，继而得到电机的反电势，然后通过反电势和电机转子位置的数学关系求得电机转子位置，最后对其求导得到转速，但是电机反电势是在低通滤波器环节通过对上一环节产生的高频振荡信号进行滤波得到的，如此就不可避免的产生相位延迟，而若是通过增加相位补偿环节，就必然使系统变得复杂，从而可能导致最终的结果不准确。因此，研究一种既能得到准确的反电势波形又不会增加可能导致过多相位滞后环节的方法成为越来越多专家学者追求的目标。

滑模变结构控制对某些影响因素具有完全的自适应性，如外部扰动、内部摄动以及系统参数变化等，即便是模型精度不高，整个系统也能正常工作，因此该控制具有很强的抗干扰性。这些优点使其在交流调速控制领域适合于大范围推广应用。本文将在PMSM控制系统中使用滑模变结构控制的方法，按照电机数学模型，构造出一个滑模变结构控制器,实现系统的无位置传感器矢量控制，并且利用锁相环方法提取转子位置角与转速，消除由滤波环节产生的相位误差。

1PMSM数学模型

PMSM控制中，常用d、q同步旋转坐标系和α、β定子静止坐标系中的数学模型。

PMSM状态方程：

电压方程：

(1)

磁链方程：

(2)

电磁转矩方程：

Te=Pnψfiβcosθ-Pnψfiαsinθ

(3)

将式(2)代入式(1)可得：

(4)

整理可得：

(5)

同理：

(6)

当：

(7)

有：

(8)

故α、β坐标系中的PMSM数学模型可写成：

(9)

一般在MATLAB仿真中PMSM的输出只有静止坐标系下的电流，需要对其进行坐标变换，将其转变为α、β坐标系下的电流值，而后滑模观测器才能将此电流作为输入值计算。

2滑模观测器设计

根据滑模变结构的理论，构造滑模观测器

(10)

其中：x∈Rn,u∈Rm,A,B(x)∈Rn*m。

此时将滑模面定义为

(11)

控制函数为

(12)

根据PMSM在α、β坐标系中的数学模型,构造滑模观测器

(13)

(14)

式中：Ksw——切换增益，其取值须满足滑模运动的存在性及可达性条件，否则系统不能进行滑模运动。

式(13)减去式(9)得：

(15)

(16)

将式(16)代入式(15)整理可得：

(17)

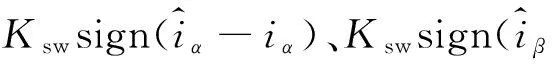
(18)

zα、zβ中包含有估算反电动势信息,因此为了得到估算反电动势的值，须使其通过低通滤波器，经过滤波可以得：

(19)

式中：ωc——低通滤波器中的截止频率。

将得出的估算反电动势值通过反正切函数的变换求得转子转角估算值

(20)

包含滑模观测器的无位置传感器PMSM控制系统框图如图1所示。

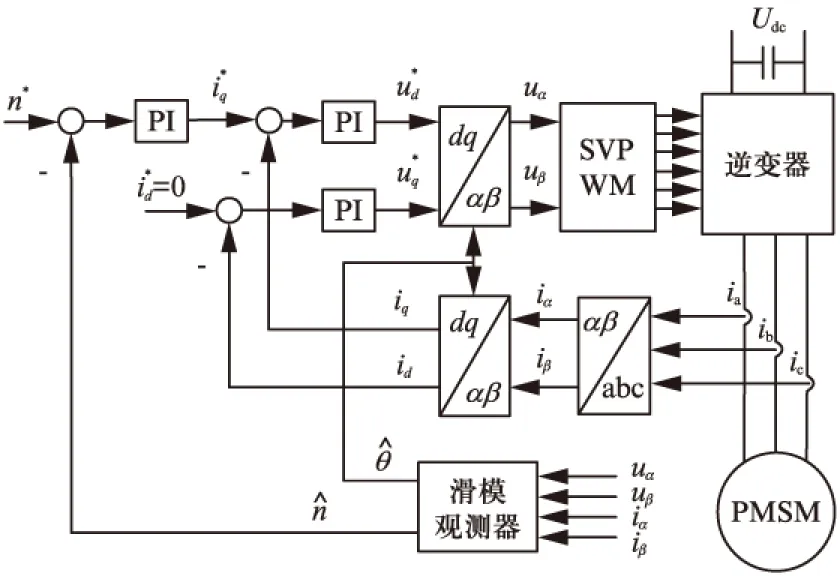
图1　PMSM无位置传感器控制系统框图

3转子位置角和转速估算

观测得到的反电势信号中包含高频噪声，通过滤波环节滤除高频噪声得到所需的连续信号，但其中会存在低通滤波器带来的相位延迟问题，并且输入信号的角频率以及滤波器的截止频率会影响到延迟的相位。因此，采用取反正切函数的方法对观测得到的反电动势进行变换得到位置信息后，须补偿相应的角度。

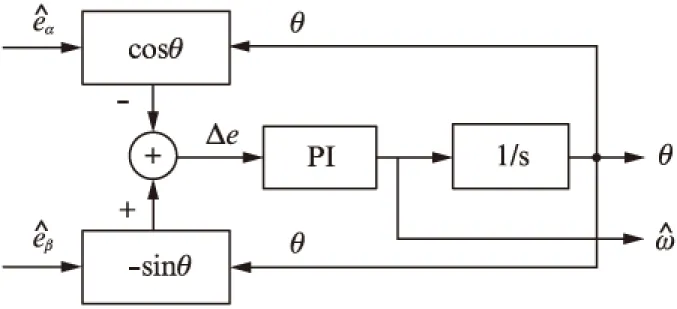
图2　锁相环结构

锁相环表达式为

(21)

由图2锁相环结构可以得到PMSM的转速与转子位置。

4仿真结果与分析

本文采用MATLAB/Simulink建立系统控制模型来验证所提出方案的可行性。电机模型由Simulink内部提供，额定相电压Us=220V，额定转速2000r/min，额定转矩Te=9.55N·M，定子电阻Rs=0.2Ω，绕组直轴和交轴电感Ld=Lq=8.5mH，转动惯量J=0.089kg·m2，永磁体磁链ψm=0.175Wb，极对数pn=4。

图3为对比的实际电流与观测电流波形。由图3中可知，观测的电流可快速准确地跟随实际电流。图4为观测电流与实际电流误差，波形显示误差在0值附近振荡,表明电流误差在滑模面上作滑模运动。

电机空载运行时，在t=0s时设定转速300r/min，t=0.5s时将转速提升为600r/min。设定转速、估计转速与实际转速波形如图5所示。

由转速波形可以看出，估计转速能够很快跟随设定转速，并且收敛于实际转速，说明系统具有良好的动、静态性能。

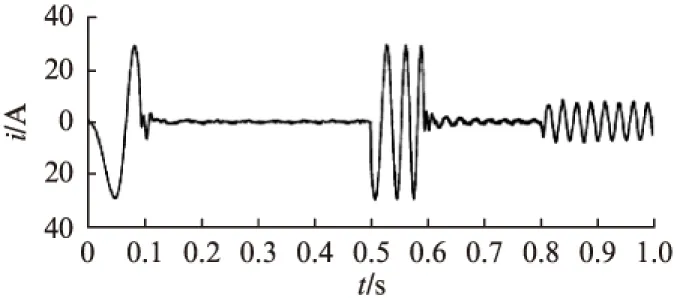
图3　实际电流与估算电流

图4　估算电流与实际电流误差

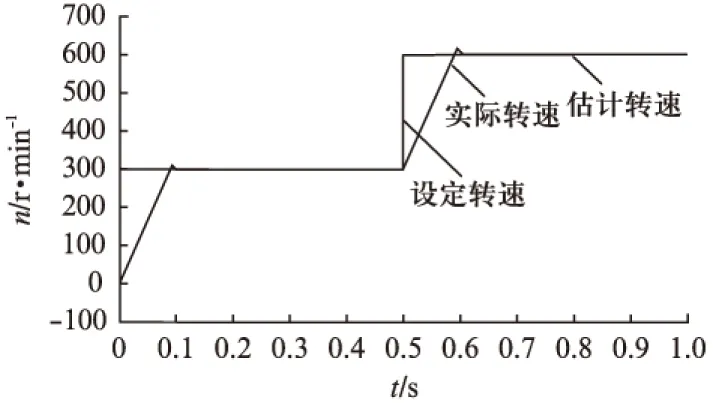
图5　转速波形

如图6(a)起动时，转速偏差约保持在5r/min，转速稳定在300r/min时，转速偏差保持在约2r/min以内。如图6(b)加速到600r/min的过程中，转速偏差约保持在5r/min，转速稳定在600r/min时，转速偏差保持在约2r/min以内。如图6(c)0.8s加载时，转速略有下降，但经过短暂调整立刻跟上设定转速，转速偏差保持在约1r/min以内。

估计转速与实际转速的偏差如图7中波形，显然，稳态时估计转速与实际转速偏差稳定在约2r/min以内，可以达到系统的控制要求。

估计扩展反电动势波形如图8所示，转速切换瞬间变化平稳，由此可以说明电机的动态性能良好。

转子估计位置与实际位置波形如图9所示，可以看出估计转子位置与实际转子位置能够保持良好的一致性，说明观测器具有良好的估计效果。

5结语

本文首先分析了PMSM的模型特点，并在此基础上，建立了包含滑模观测器的PMSM无位置传感器转速和转角模型，将估计和实际电流值之差作为切换函数输入观测器，通过持续获取两者之间的误差来改变系统结构，最终达到使两者的误差渐渐变小直至两者趋近一致的目的。采用滑模观测器观测反电动势，为消除参数变化和系统不确定性带来的不利影响，需要选择合适的滑模增益，并利用锁相环估算转子位置和转速，同时在补偿转子位置角的前提下，准确估算出转子位置和转速。仿真波形显示，提出的策略可使系统较准确地检测出转子空间位置和转速，且此系统动态及静态等各方面性能表现良好，是一种可实现交流调速控制系统无位置传感器运行的新策略。

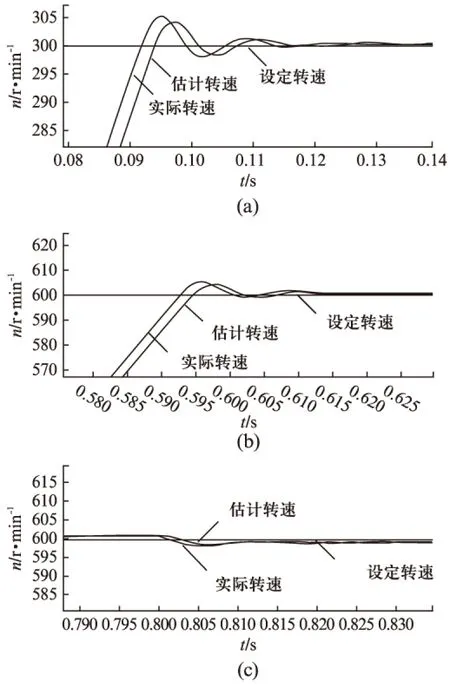
图6　起动、加速、加载时转速局部放大图

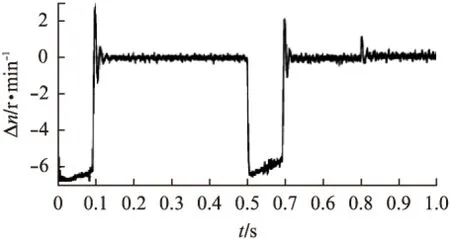
图7　估计与实际转速偏差

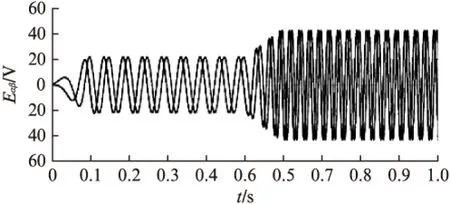
图8　估计扩展反电动势

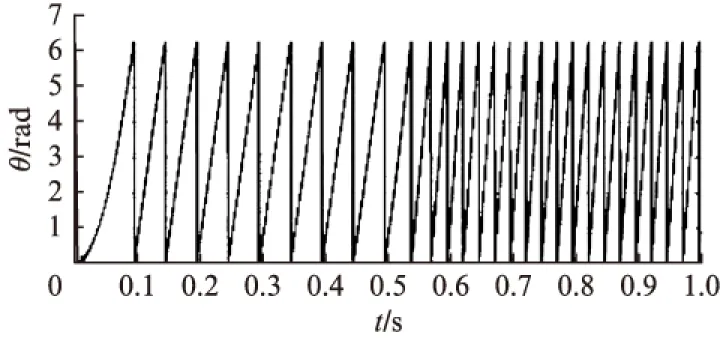
图9　实际转子位置角和估计转子位置角

【参 考 文 献】

[1]张洪帅，王平，韩邦成，等.基于模糊滑模观测器的磁悬浮高速永磁同步电机转子位置检测方法.电工技术学报，2014，29(7)： 147-153.

[2]KUNG Y S， QUYNH N V， HUANG C C， et al.Design and simulation of adaptive speed control for SMO-based sensorless PMSM drive.International Conference on Intelligent and Advanced Systems(ICIAS)，2012(1)： 439-444.

[3]张晓光，孙力，陈小龙，等.基于二阶滑模观测器的永磁同步电机无位置传感器控制.电力自动化设备，2013，33(8)： 36-40.

[4]易伯瑜，康龙云，陶思念，等.永磁同步电机抗扰高阶滑模观测器设计.电工技术学报，2014，29(5)： 132-140.

[5]刘波，徐政，陈锐坚，等.PMSM转子初始位置检测方法的研究与应用.电气传动，2013，43(10)： 18-22.

[6]NOHARA S， TOMITA M， HASEGAWA M，et al.A new design method of full-order extended electromotive force observer for position sensorless control of IPMSM.Industrial Electronics Society，IECON 2013-39th Annual Conference of the IEEE. 10-13 Nov. 2013： 2512-2517.

[7]刘军，王刚，俞金寿.基于卡尔曼滤波器SMO的永磁同步电机无传感器矢量控制.电机与控制应用，2010，37(2)： 21-24.

[8]王丰尧.滑模变结构控制.北京： 机械工业出版社，1998

[9]刘金琨.滑模变结构控制MATLAB仿真.2版.北京： 清华大学出版社，2012.

[10]陆婋泉，林鹤云，冯弈，等.永磁同步电机无传感器控制的软开关滑模观测器.电工技术学报，2015，30(2)： 106-113.

[11]刘艳莉，张烨，吕继考，等.PMSM改进型滑模观测器无传感器参数辨识.电力系统及其自动化学报，2014，26(4)： 30-34.

[12]慎翔，李红梅.基于改进磁链观测法的PMSM无位置传感器控制.微电机，2012，45(7)： 55-59.

*基金项目：国家重大科学仪器设备开发专项资助项目(2012YQ15008703)

作者简介：张曲遥(1987—)，男，硕士研究生，暂无职称，研究方向为永磁同步电机无速度传感器控制。 高艳霞(1958—)，女，硕士研究生，副教授，研究方向为开关电源技术和电力电子系统建模及系统性能研究。 宋文祥(1973—)，男，博士研究生，教授，研究方向为交流电机驱动控制及应用和新型电力电子变换。

中图分类号：TM 301.2

文献标志码：A

文章编号：1673-6540(2016)06- 0034- 05

收稿日期：2015-10-26

Sliding Mode Observer Based Position Sensorless Control of PMSM*

ZHANGQuyao,GAOYanxia,CHENJing,SONGWenxiang

(College of Mechatronics Engineering and Automation, Shanghai University, Shanghai 200072, China)

Abstract：A sliding mode observer(SMO) based position sensorless control method was presented for permanent magnet synchronous motor. Through the depth analysis of mathematical model of PMSM in static coordinate system,a sliding mode observer was proposed to estimate the speed of the position sensorless PMSM.Furthermore, in order to eliminate the phase delay caused by the low pass filter to get more accurate velocity. A phase-locked loop was constructed by using the position of the rotor and the back electromotive force from the observer. The speed of the motor was obtained by proportional integral of the input signal in the phase locked loop. Simulation results were provided to verify its feasibility and effectiveness.

Key words：permanent magnet synchronous motor(PMSM); position sensorless control; sliding mode observer; phase locked loop(PLL)