路基不均匀沉降对路面结构影响的数值分析

张中云

（1.苏交科集团股份有限公司，江苏 南京 211112；2.新型道路材料国家工程实验室，江苏 南京 211112）

·道路工程·

路基不均匀沉降对路面结构影响的数值分析

张中云1，2

（1.苏交科集团股份有限公司，江苏 南京 211112；2.新型道路材料国家工程实验室，江苏 南京 211112）

文章依托某扩建工程，对路基拼接引起的不均匀沉降对路面结构影响进行数值分析。研究表明，新老路堤表面施工期末最大差异沉降值为6.869 cm，新老路堤表面各点的工后沉降值从路堤中心线向外不断减小，路堤中心处沉降值最大为6.12 cm，不均匀沉降为1.17 cm，路面各层结构受力均在允许范围内。

路基工程；路基拼接；不均匀沉降；数值分析

老路拓宽建设时期，老路固结沉降以及次固结沉降已基本结束，地基已趋于稳定。对于拓宽路段，初始沉降可以在建设期间完成，但固结沉降与次固结沉降是一个长期的过程，在运营期间将会继续发生。老路与新建路之间的差异沉降加上荷载的不均匀性，使得新老路基的沉降变形特性存在较大的差异，对路面结构的受力具有显著的影响［1］。本文对路基不均匀沉降对路面结构的影响进行了数值分析，为旧路拼接提供良好的设计参数，并为以后旧路拓宽工程提供技术支撑。

1 新老路基沉降数值分析

1.1 数值分析方法概述

由于岩土工程的复杂性和特殊性，数值模拟作为解决岩土工程问题的有效手段，已越来越多地应用于岩土体稳定性、岩土工程设计和岩土工程基本问题分析中［2］。

本文采用拉格朗日法对路基地基沉降特性进行数值模拟，在本文数值分析中，做了如下一些假设：（1） 按平面应变问题处理；（2）路堤填土和地基土的本构关系采用Mohr-Coulomb理想弹塑性本构模型；（3）地基土中地下水位以下的土体考虑土的固结；（4）采用初始应力状态和时间步技术模拟新老路路堤的先期固结和分步加载。

1.2 新老路基地基的几何参数

原路堤宽度为13 m，双侧拓宽宽度为8 m。路堤填土高度为3.5 m，地基土层的厚度取40 m（分4层），地基横向宽度取100 m。

1.3 加荷历程

为了模拟实际的新老路堤拼接施工过程，将整个计算过程分为4个时段，即老路堤施工加载期、老路堤工后固结期、新路堤施工加载期和工后固结期［3］。为了真实模拟新旧路堤的逐层施工，将路堤分为6层进行增量分析。其中，老路运营一定年限后进行拓宽，拓宽路堤施工期为13个月，设计年限为15年。

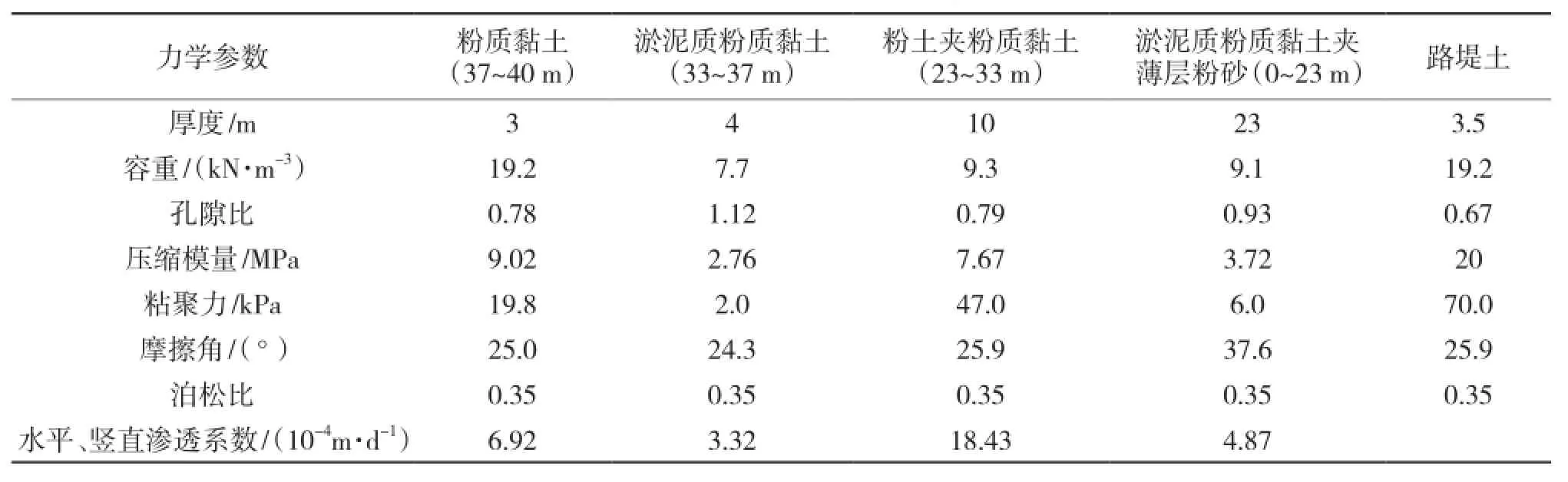
表1 地基和路基填料物理力学参数

1.4 计算参数

地基和路堤填料所用的具体参数如表1所示。

1.5 网格划分和边界条件

地基是一个半无限的空间，在进行数值分析时只能取一个有限的区域进行计算，常常将三维空间问题简化为二维平面问题处理。地基和路堤看成平面应变问题分析。地基计算深度取40 m，计算宽度取100 m。本文数值分析方法采用四边形单元划分网格，网格划分如图1所示。

图1 地基路基网格划分

根据路基横断面的对称性，网格划分取结构的一半。其中，结构左右边界均为横向固定约束，无水平位移，不排水；结构前后方向边界均为沿线路方向固定约束，无纵向位移，不排水；底部为固定约束，无水平、竖直和纵向位移，不排水；上边界各方向均自由，排水；地下水位线为地表处。

非线性计算中，计算前首先就要确定加荷前初始应力状态。作为近似估计，采用土体的自重应力。本文在以下分析新老路堤变形过程中，对老路堤已经发生的固结沉降不作深入研究，主要是分析新路堤施工后对老路堤产生的附加变形。故在计算路堤沉降过程中不考虑老路堤已经发生的沉降。

1.6 拓宽后新老路基的变形

拓宽路堤15年固结期末新老路堤沉降云图如图2所示。从沉降云图可知在拓宽路堤15年固结期末，新老路堤的整体沉降由老路堤中心处向拓宽路堤方向逐渐增大，到达拓宽路堤形心附近时沉降达到最大值，然后向外又逐渐减小至道路外边缘。

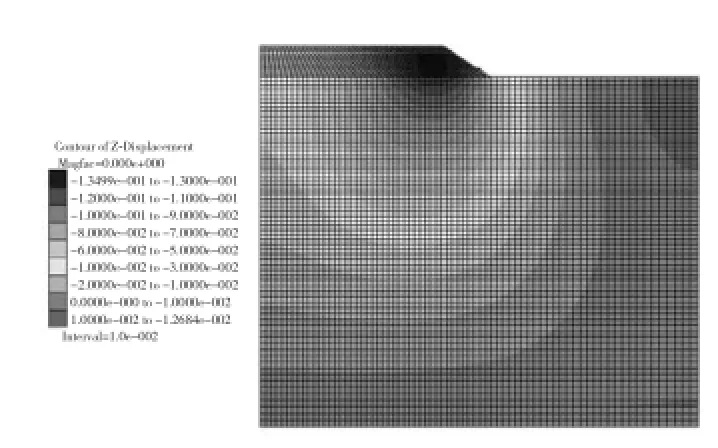
图2 拓宽后新老路堤沉降云图

根据路基横断面的对称性，网格划分取结构的一半。其中，结构左右边界均为横向固定约束，无水平位移，不排水；结构前后方向边界均为沿线路方向固定约束，无纵向位移，不排水；底部为固定约束，无水平、竖直和纵向位移，不排水；上边界各方向均自由，排水；地下水位线为地表处［4］。

新老路堤表面的沉降曲线及工后沉降曲线分别如图3、图4所示。

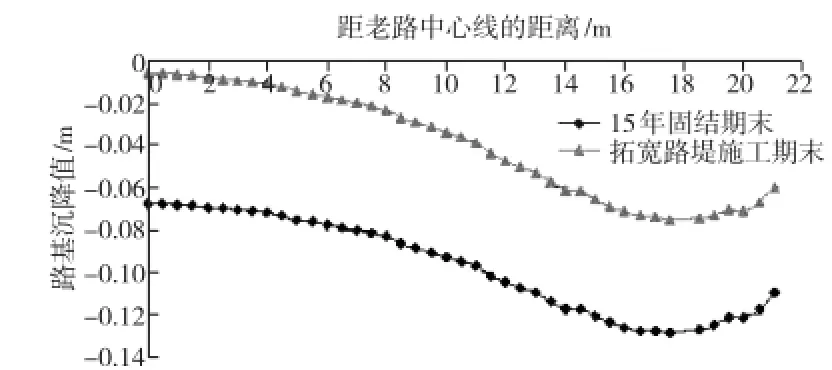
图3 新老路堤表面的沉降曲线

从图4可以看出，新老路堤表面各点的工后沉降曲线近似呈现正盆形，从路堤中心线向外，沉降值不断减小，在路堤中心处取得最大值6.12 cm，其中，老路表面（距离老路中心0～13 m）的工后差异沉降率为0.34‰，拓宽路堤表面（距离老路中心13～21 m）的工后差异率为9.02‰，新老路0～21 m范围内工后差异沉降率为0.56‰，即不均匀沉降为1.17 cm。

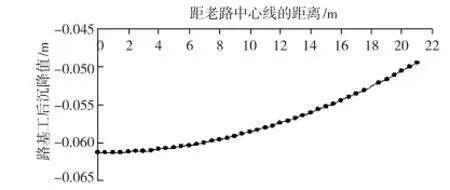
图4 新老路堤表面的工后沉降曲线

2 不均匀沉降对路面结构的响应

新老路基间的差异沉降的大小与拉应力有着密切的关系，当新老路基间的差异沉降达到一定数值时，这种不均匀沉降会使得路面结构层中产生附加应力，当附加应力大于路面结构层的容许拉应力时，路面结构层将发生破坏。本文对新老路基地基的不均匀沉降对路面结构层的影响进行分析，并与路面各结构层抗拉强度进行对比分析，从而为路面材料的选择提供理论依据。

2.1 不均匀沉降分布模式

对于双侧拓宽的路基，在路基的横断面方向，路基加宽部分的中心沉降量大，两侧沉降量较小（如图5所示），本文采用余弦曲线对其进行拟合，沉降方程如下：

式中：δmax为路堤拓宽中点最大工后沉降量；B为1/2拓宽部分路基宽度。

图5 公路工后沉降分布示意图

拟合结果如图6所示，由图6可知，余弦曲线对数值模拟的计算结果进行拟合，拟合效果较好。

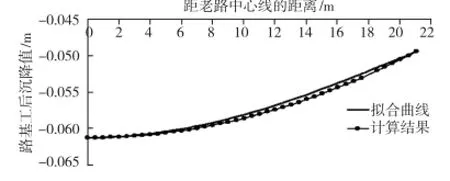
图6 新老路堤表面的工后沉降与拟合后曲线

2.2 计算模型

本次路基拼接中路面为沥青混凝土路面。沥青混凝土路面分为4层体系进行分析，计算模型如图7所示。

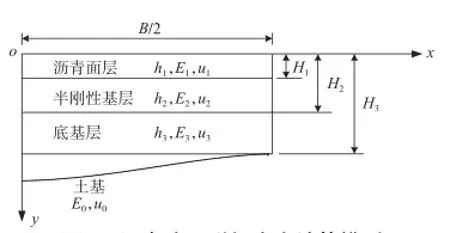
图7 沥青路面附加应力计算模型

计算中采用如下假定：

（1） 路面各结构层为连续均质、各向同性线弹性材料，力学特性用弹性模量E和泊松比μ表征；

（2） 路面各结构层在垂直方向完全连续，即路基不均匀沉降随使用时间缓慢增长，路面各结构层在交通荷载与自重作用下随之下沉，层间不会出现脱空现象；面层、基层和底基层间为连续接触条件，考虑到底基层材料与路基之间变形的不协调性，其层间处理为光滑接触条件；

（3）均匀的路基下沉对路面结构的影响不大，故只考虑不均匀沉降引起的附加应力；

（4）按平面应变问题分析。

2.3 计算参数的选取

路面宽度为42 m，沥青路面结构层总厚度为74 cm，各结构层材料参数取值如表2所示。

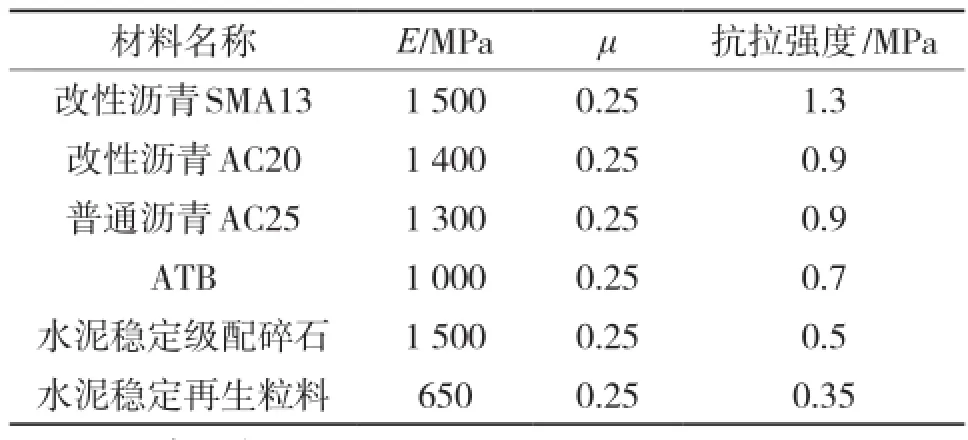
表2 路面各结构层材料参数

2.4 计算分析与结论

本文中的路基地基的不均匀沉降值为1.17 cm，路面的受力分析如图8所示，附加应力计算结果如图9所示。

图8 不均匀沉降1.17 cm的附加应力计算模型

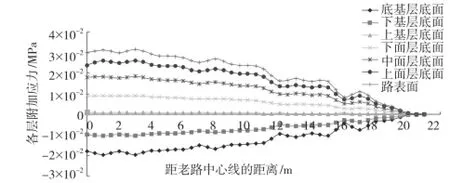
图9 不均匀沉降为1.17 cm的附加应力计算结果

由图9可知，路面不均匀沉降为1.17cm时，沥青路面受压力，基层及底基层下层受拉力，但所受拉力均远远小于各结构层的抗拉强度。

3 结论

（1）新老路堤表施工期末最大差异沉降值为6.869 cm；

（2）新老路堤表面各点的工后沉降曲线近似呈现正盆形，从路堤中心线向外，沉降值不断减小，在路堤中心处取得最大值6.12 cm，不均匀沉降为1.17 cm；

（3）在不均匀沉降作用下，路面各层结构受力均在允许范围内。

［1］桂炎德，徐立新.沪杭甬高速公路（红垦至沽渚段）拓宽工程设计方法［J］.华东公路，2001（6）：3-6.

［2］Richard J. Deschamps，Christopher S. Hynes，Philippe Bourdeau，Embankment widening design guidelines and construction procedures［R］. Research Project Final Report：Purdue University，1999.

［3］李又云.同时考虑加荷、变形和时间的公路软基固结沉降理论及仿真的研究［D］.西安：西安公路交通大学，2000.

［4］唐朝生，刘义怀，施斌，等.新老路基拼接中差异沉降的数值模拟［J］.中国公路学报，2007，20（2）：13-17.

Numerical Analysis of Influence of Differential Subgrade Settlement on Pavement Structure

Zhang Zhongyun1，2
（1. JSTI Group， Nanjing 211112， China； 2. National Engineering Laboratory for Advanced Road Materials， Nanjing 211112， China）

Taking an extended engineering as a background， the paper analyzes the influence of differential subgrade settlement on pavement structure. The results show that the maximum differential settlement is 6.869cm on the surface of new and old subgrade in final construction period. The post-construction settlements of old and new subgrade surface are gradually decreasing from the center line of embankment， the maximum settlement value is 6.12 cm at the center line of the subgrade， and differential settlement is 1.17cm， pavement structure stress of each layer is within the scope of the permit.

subgrade engineering； subgrade connecting； differential settlement； numerical analysis

U416.1

A

1672-9889（2016）01-0001-03

广东省交通厅科技项目（项目编号：2005-02-07）

张中云（1979-），女，辽宁朝阳人，工程师，主要从事道路工程设计工作。

2015-04-20）