空间钢网格盒式结构的随机地震响应研究

白志强, 马克俭, 刘文锋

(1.贵州大学 空间结构研究中心，贵阳　550003； 2.潍坊学院 建筑工程学院，山东 潍坊　261061;3.青岛理工大学 土木工程学院，山东 青岛　266033)



空间钢网格盒式结构的随机地震响应研究

白志强1,2, 马克俭1, 刘文锋3

(1.贵州大学 空间结构研究中心，贵阳550003； 2.潍坊学院 建筑工程学院，山东 潍坊261061;3.青岛理工大学 土木工程学院，山东 青岛266033)

摘要：给出了空间钢网格盒式结构地震反应运动方程，利用复模态理论推导了盒式结构体系的时域闭合解和随机响应闭合解。假定随机响应符合极值Ⅰ型分布，给出了结构响应的可靠度计算公式。利用随机响应的峰值因子和变异系数，构建了随机响应给定概率的置信区间。以南京多功能展厅为工程背景，以KANAI-TAJIMI功率谱作为随机激励，计算了空间钢网格盒式结构的随机响应峰值和方差；同时选用14条强震记录作为确定性激励，得到盒式结构复模态时程响应峰值。计算结果表明，两种方法所得结果具有一致性。随机地震响应方法可作为盒式结构这一新型结构体系的补充计算方法，也可用于估计和校核确定性时程响应的可靠程度。

关键词：盒式结构；复模态；随机响应分析；可靠度；区间估计

空间钢网格盒式结构是我国拥有独立知识产权的，适用于大跨建筑的新型节能结构体系[1-2],自2010年发明以来，该体系已在贵州、湖南等省份推广应用。该结构体系由四面钢网格墙架和钢网格空腹夹层板组成基本盒子单元，若干个盒子叠合形成整体空间受力体系。其特点是结构自重轻，整体受力均匀；装配化程度高，施工方便；使用功能与结构受力相辅相成，节约综合造价。基本盒子单元组装模型如图1～图3所示。

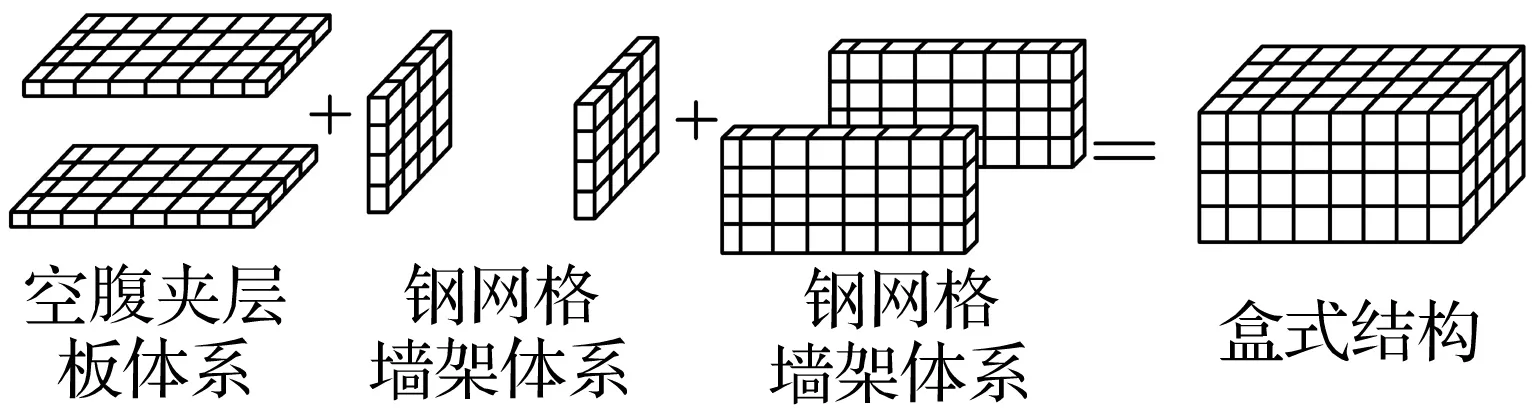
图1　基本盒子单元组成Fig.1 The steel grid-box-structure composed of assembly units

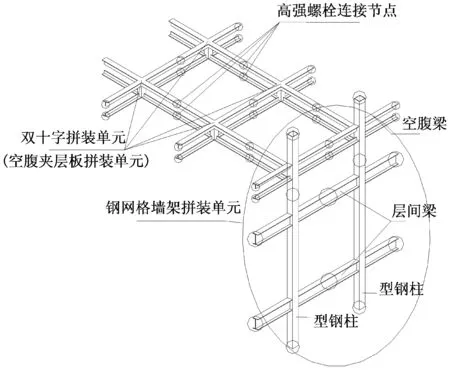
图2　盒式结构拼装节点示意图Fig.2 Joints’ details for the assembly units

图3　空间钢网格盒式结构工程实例Fig.3 A practical case of the steel grid-box-structure

空腹夹层板是盒式结构的水平受力体系，是组成盒式结构的关键构件。盒式结构的早期研究主要集中在对空腹夹层板的静动力性能的理论或实验研究[3-6]，以及对墙架体系的抗震性能研究[7]。文献[8]对混凝土盒式结构体系的受力及抗震性能进行了系统研究。令人遗憾的是，已有的研究成果均是在确定性地震激励下的研究成果。由于断层机制、震源特点、传播途径等因素的不确定性，地震作用具有强烈的随机性，用随机振动理论分析结构受力，考察结构的随机响应无疑是更加合理的。自从Housner提出用白噪声来模拟地震加速度过程以来，经过几十年的研究，已得到一些较好的随机模型，其中研究较多的是Kanai-Tajimi谱[9]。利用抗震规范研究地震随机模型参数是促进随机振动理论应用到结构设计领域的一种主要思路，文献[10-11]建立了与我国抗震规范相一致的随机地震动参数。欧洲抗震规范(EUROCODE 8)和中国公路桥梁抗震设计细则(JTG/TB 02-1—2008)已将随机振动分析方法列为抗震设计方法之一[12-13]。

尽管传统结构基于确定性激励下的地震响应具有一定的离散性，但大量工程经验的积累在一定程度上可以弥补这种不足。盒式结构作为一种新体系，工程实践相对较少，相关行业规程远没有形成体系，确定性结果的离散性难以估计。因此，用随机分析方法研究盒式结构受力性能尤显重要而紧迫。本文建立钢网格盒式结构的动力微分方程，进行随机反应分析，得到结构随机地震顶点位移和层间位移统计特征解。在此基础上，构建极值Ⅰ分布样本空间，考察各确定激励下结构反应的可靠度，为指导该新型体系的工程实践提供理论依据。

本文以南京中建化工多功能展厅的钢网格盒式结构方案为工程算例，采用Kanai-Tajimi模型作为随机激励，计算结构的随机响应，构建概率样本空间。在此基础上，选取14条地震波激励，得出多遇地震下的层间位移，考察钢网格盒式结构的层间位移响应和顶点位移响应可靠度。

1盒式结构的动力微分方程

在进行整体计算时，盒式结构的空腹夹层板可看作刚性隔板，不考虑面内弹性变形，多层钢网格墙架的侧移曲线仍然为剪切型[3]，因此其层刚度可采用D值法结合图4近似计算:

图4　空间钢网格盒式结构墙架层间刚度计算示意Fig.4 A steel grillage wall of the box-structure

(1)

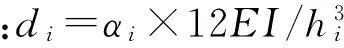
盒式结构的运动方程为：

(2)

2复模态时程分析方法

复模态分析方法能够得到理论上的解析解，因此可将式(2)经Foss变换后表示为[14-15]

(3)

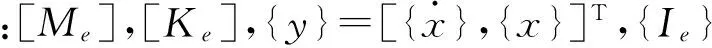
式(3)的广义特征值为2n个复特征值，且共轭成对出现，记作：λ1,λ2,…,λn;λn+1,λn+2,…,λ2n。2n个复特征值对应2n个复特征向量，第j复振型可表示：

2n个{Φej}组成2n×2n振型方阵：

[Φe]=[{Φe1},{Φe2},…,{Φe2n}]

λj称为结构体系的第j阶复频率，表示如下：

2n个复频率λj为对角元素的对角方阵：

foss变量代换关系为：

(4)

再利用复模态在2n维状态空间的正交性，变换式(2)为：

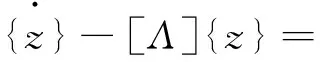
(5)

(6)

通过变量代换，式(5)的解可表示为[10]

(7)

式中：hj(ξ)为结构振动脉响函数；由式(4)的变化代换关系可反推出可得原结构响应。

3盒式结构的随机响应

根据随机振动理论，当随机干扰的均值为零时，其相关函数与谱密度存在下列关系

(8)

3.1随机地震动模型的确定

多层大跨盒式结构的基本自振周期一般都在1～3 s之间，整体结构振动频率处于中高频域，因此采用Kanai-Tajimi模型作为随机地震动激励是合适的，其功率谱密度函数为

(9)

式中S0为白噪声的谱密度，即谱强度因子，ζg，ωg分别为地基土的阻尼比和特征频率。取值参考文献[10]。

3.2随机反应的均方差

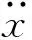
CFe(τ)=E[{Fe(t)}{Fe(t+τ)}T]=

A·ATE[{xg(t)}{xg(t+τ)}T]=

(10)

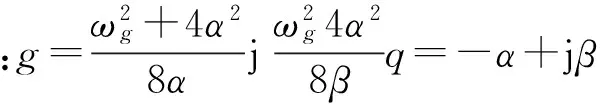
由式(7)可得复模态响应矢量的协方差矩阵为：

利用脉响函数表达式做二重积分：

τ≥0

(11)

式中：

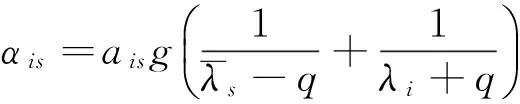
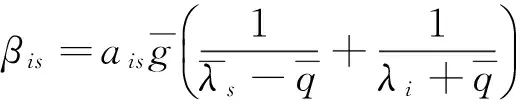
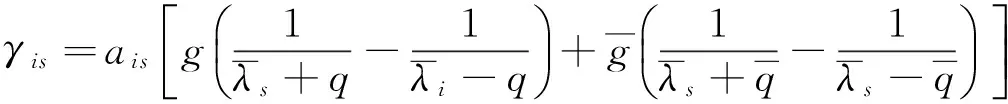
(i，s=1，2，……2n)

3.3随机反应峰值因子的确定

由随机振动理论[16-17]，线性体系最大反应往往发生在地震激励的平稳段。因此我们将随机地震动激励看作是平稳随机过程，将平稳激励下的结构体系反应也近似看成平稳随机过程。

假设平稳反应为X(t)，它的相关函数与谱密度之间的关系为：

(12)

式中:τ=t2t1；SX(ω)、RX(τ)分别为体系反应的谱密度函数和相关函数。

根据推导，体系平稳反应的谱密度函数和平稳激励的谱密度函数存在下列关系：

(13)

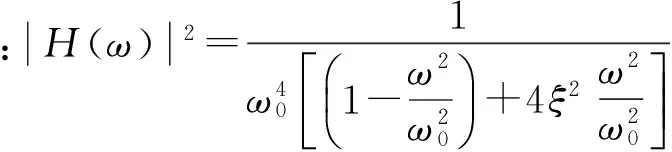
平稳反应的速度谱密度和位移谱密度存在下列关系：

(14)

结合式(11)可得：

(15)

则有：

式中:λ0和λ2为反应的零阶和二阶谱矩，v为加速度的期望交零率。

则峰值因子r存在下列关系：

像宋国朴一样在景区打工的村民还有不少，有看大门的、管停车场的、守护河道安全的。景区每年夏季招聘150多人从事旅游服务，还有更多村民做起漂流鞋、喷水枪等漂流用品生意。“漂流景区一开业，整个村子都忙起来了，一个夏季的劳务及经营收入能突破1000万元。”曾兆童说。

(16)

式中:td为地震动持时，取值参考文献[12]。

3.4随机最大反应均值

根据随机振动理论，线性结构体系在平稳地震激励作用下随机最大反应均值可由下式给出：

am=rσa

(17)

式中：r为峰值因子，σa为随机反应均方差，am为随机最大反应均值。

3.5随机位移响应区间估计[18]

由于位移指标能直观地描述结构的破坏过程，规范通常对结构层间位移进行限值控制，以期实现相应的抗震目标。在求得随机层间位移响应和顶点位移响应之后，利用首次超越破坏机制，可计算位移响应的可靠度。根据文献[19]研究结果，钢结构层间位移最大值与极值Ⅰ型分布最为吻合，因此结构位移响应的概率分布函数可表示为

(18)

式中:T=σam/1.282 5，k=σa-0.577 2 T。其中σam和σa分别为结构位移的最大值均方差和最大值方差，根据文献[19]的研究结果，取变异系数为0.3，则σam=0.3σa；x为结构体系层间位移或顶点位移响应最大值，根据分布函数的定义可知，x在置信区间(x1,x2]的可靠度为

Pr=F(x2)-F(x1)

(19)

式中，x1和x2分别为置信区间下限值、上限值，可通过响应均值和方差按一定概率设置。

3.6随机位移响应可靠度

Pr=F(b)

(20)

4盒式结构算例分析

南京中建化工多功能展厅的钢结构部分采用四层钢网格盒式结构新体系。建筑平面尺寸为39 m×23.4 m，结构四层，底层结构层高9.0 m，其余三层层高为4.8 m，一层设置两道层间梁(h1=3 m,h2=3 m,h3=3 m)，二至四层设置一道层间梁(h1=1.1 m,h2=3.7 m)；不上人屋面。按各层恒载活载换算成各层重力荷载代表值，经计算为：m1=789.35 t，m2=m3=884.65 t，m4=976.75 t；各层抗侧刚度经过计算分别为：k1=D1=80 713 kN/m，k2=D2=258 849 kN/m，k3=D3=294 302 kN/m,k4=D4=291 833 kN/m。

4.1复模态时程分析和随机响应分析

选取包括集集地震、墨西哥地震等在内的144条地震波进行频谱分析，根据抗震规范场地土特征周期对地震波分组，选取Ⅳ类场地第三组的14条地震波作为确定性地震激励，对盒式结构进行复模态时程分析(确定性分析)，得到14个确定解；同时进行复模态随机反应分析，得到结构位移响应统计特征值：层间位移反应最大值均值和顶点位移最大值均值。两种方法计算结果如表1所示。

由表1得知，14个确定解的平均值与随机反应分析方法的层间位移和顶点位移统计特征值基本一致，层间位移相对误差为(0.002 61～0.002 52)/0.002 61=3.66%,顶点位移相对误差为(0.044 1～0.042 7)/0.044 1=3.10%。

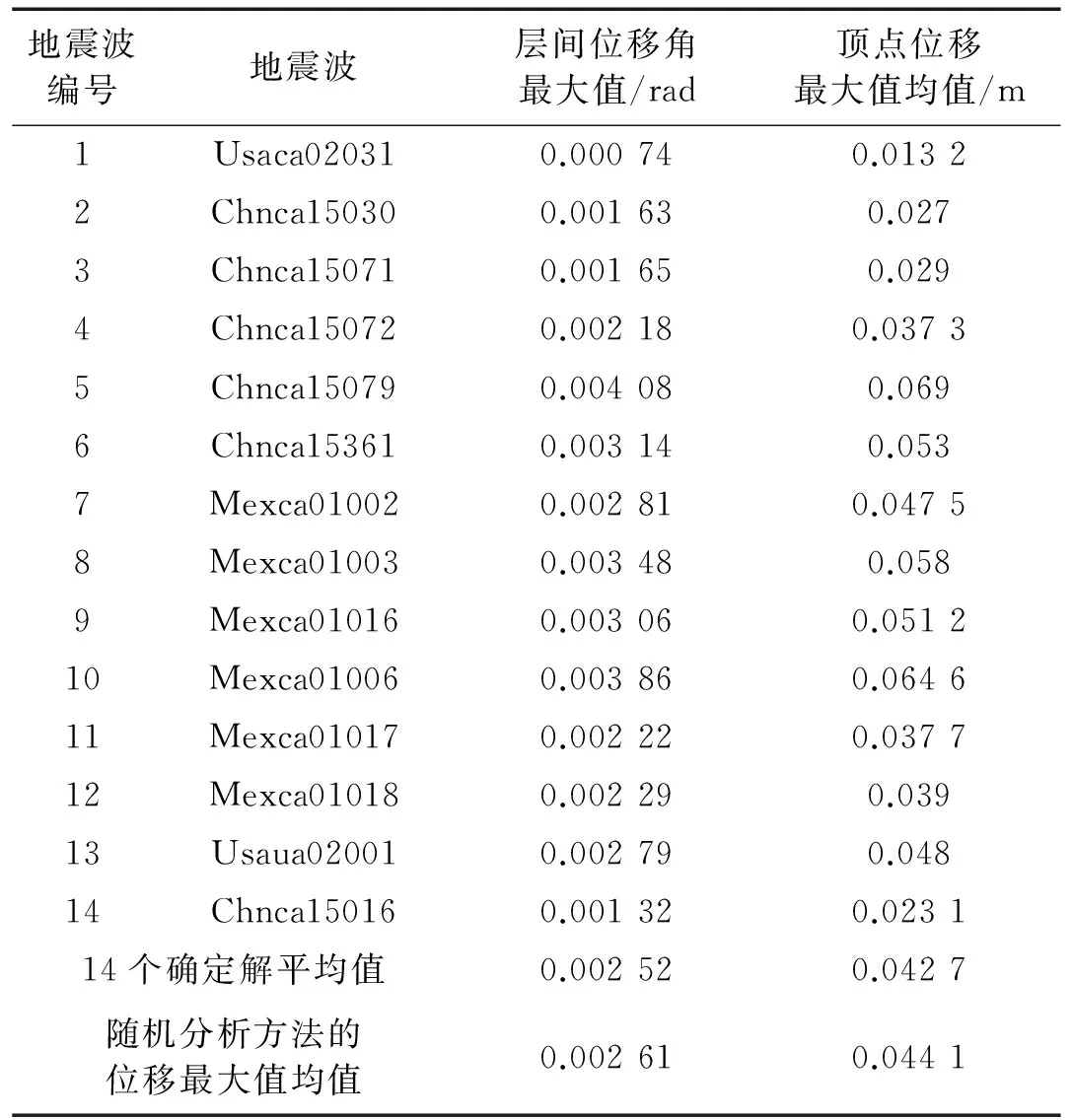
表1　 用两种方法计算的结构位移最大值

为进一步验证随机分析方法结果的可靠性，采用区间估计法，在求得随机响应统计特征值的基础上构建层间位移最大值置信区间[σm-2σam，σm+2σam]，层间位移按极值Ⅰ型分布函数计算样本区间概率为0.957 7。将14个确定解与区间画在同一个坐标系下，见图5和图6。

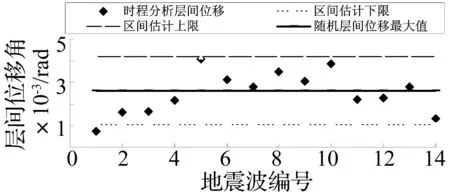
图5　确定激励下层间位移最大值分布Fig.5 The maximum distribution of structural story drift angles solved by the two methods

图6　确定性激励下顶点位移最大值分布Fig.6 The maximum distribution of structural top floor displacements based on the two methods

从图5和图6可以看出，层间位移和顶点位移的14个确定解基本都在预测概率为0.957 7的置信区间内，其中有7个确定解分布在随机方法所得层间位移均值附近。因此可以认为两种方法计算结果在统计意义上是一致的。

4.2规范中层间位移限值可靠度

我国规范中通过控制层间位移角实现多遇地震和罕遇地震水准下的结构抗震性态。钢结构在多遇地震作用下的层间位移限值为1/250。

由随机分析方法，得到盒式结构层间位移最大值均值σa=0.002 61 m，则其方差为σam=0.3×σa=0.000 783 m，b=1/250，代入式(18)中得到：

T=0.000 611，k=0.002 26

即多遇地震下规范的层间位移限值可靠度为94.37%。

4.3地震波激励下的位移响应可靠度

我国抗震规范规定对特殊结构应进行多遇地震下的时程分析补充计算，盒式结构作为一种新体系，有必要采取时程分析方法作为补充计算。地震波的实际地震记录仅通过卓越周期进行分组归类显然过于粗略，若将4.2节求得的规范弹性层间位移角限值可靠度0.943 7作为参考指标，将表1中14个确定性激励下的层间位移最大值视为式(18)中的x，求得14条地震波对应的层间位移可靠指标，列于图7中。

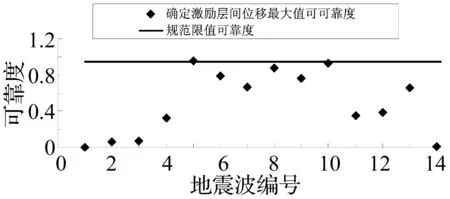
图7　 14条地震波作用下的结构层间位移可靠度Fig.7 The reliability of 14 story drift angles based on the method of complex modal time analysis

由图7可知，与规范弹性层间位移角限值可靠度较为接近的地震波为第5条地震波(Chnca15079)

第8条地震波(Mexca01003)、第10条地震波(Mexca01006)。说明这三条地震波的频谱成分与规范反应谱方法最为吻合，因此可作为盒式结构时程分析方法地震选波时优先考虑，使得计算结果更具有代表性。

5结论

本文分别用基于复模态的时程分析和随机反应分析两种方法对空间钢网格盒式结构进行了计算，两种方法具有统计意义上的一致性，并进一步得出以下结论：

(1) 单条地震波时程分析的计算结果存在一定的偶然性和离散性，但基本能控制在随机反应最大均值上下2倍方差的范围内。

(2)KAI-TAJIMI谱作为多层钢网格盒式结构的随机功率谱是合适的，可通过随机反应响应特征值估计单条地震波激励下的层间位移离散程度。

(3)通过计算盒式结构的层间位移可靠度可知，规范指标限值适用于盒式结构抗震设计，可作为盒式结构设计控制指标，具有较高的可靠度。

(4)通过可靠性分析可知，地震波激励下的结构响应可靠度具有明显的离散性，在进行确定性分析时，优先考虑结构层间位移角可靠度水平一致的地震波作为地震激励，进行结构设计。

参 考 文 献

[1] 马克俭.田睿,栾焕强. 一种用于震区的装配整体式空间钢网格盒式结构房:201410722328.4 [P].2015-3-25.

[2] 马克俭，陈靖，田啟良.一种装配整体式正交斜放混合型钢网格盒式结构:201510186387.9[P]. 2015-7-15.

[3] 黄勇，马克俭，陈波. 多层空腹夹层板柱结构的动力特性研究[J]. 建筑结构学报，2000，21(3)：23-29.

HUANG Yong, MA Ke-jian, CHEN Bo. The study of dynamic behavior for multi-storied vierendeel sandwich plate-column structure[J]. Journal of Building Structures, 2000，21(3)：23-29.

[4] 马克俭，张华刚,黄勇,等. 大跨度钢筋混凝土空腹板柱结构的研究与应用[J]. 建筑结构学报，2000，21(6)：16-23.

MA Ke-jian,ZHANG Hua-gang, HUANG Yong,et al. Study and application of long span reinforced concrete vierendeel sandwich plate [J]. Journal of Building Structures, 2000，21(6)：16-23.

[5] 黄勇，宋佳，段俞忠. 33 m跨度组合空腹楼盖设计及测试[J].建筑结构学报，2006，27(2)：88-93.

HUANG Yong, SONG Jia,DUAN Yu-zhong. Design and test of 33 m-span composite open-web plate[J]. Journal of Building Structures, 2006，27(2)：88-93.

[6] 黄勇，刘静,周理，等. 组合空腹板架结构研究与应用[J].建筑结构学报，2007(增刊1)：195-201.

HUANG Yong, LIU Jing,ZHOU Li, et al. Researches and application of composite open-web plate[J]. Journal of Building Structures, 2007(Sup1)：195-201.

[7] 孙涛，马克俭, 陈志华,等. 多层石膏墙体钢网格框架结构影响系数研究[J].建筑结构学报，2013，34(9)：66-72.

SUN Tao, MA Ke-jian, CHEN Zhi-hua, et al. Study on structural influencing coefficeient of multistory steel grid frame with gypsum-wall[J]. Journal of Building Structures, 2013，34(9)：66-72.

[8] 王其明. 现浇石膏外墙钢筋砼高层网格盒式筒中筒结构研究与应用[D].天津:天津大学，2012,11.

[9] Kanai K. An empirical formula for the spectrum of strong earthquake motions[J]. Bull Earthquake Res Inst, Univ Tokyo, 1961,39: 85-95.

[10] 薛素铎.王雪生.曹资.基于新抗震规范的地震动随机模型参数研究[J]. 土木工程学报，2003，36(5)：5-10.

XUE Su-duo, WANG Xue-sheng, CAO Zi.Parameters study on seismic random model based on the new seismic code[J]. Chian Civil Engineering Journal,2003，36(5)：5-10.

[11] 白国良.朱丽华.基于现行抗震规范的Kanai-Tajimi模型参数研究[J]. 世界地震工程，2004， 20(3)：114-118.

BAI Guo-liang, ZHU Li-hua. Study on the parameters of Kanai-Tajimi model based on the code(GB 50011—2001)[J]. World Earthquake Engineering,2004， 20(3)：114-118.

[12] EC8 (2004) .Eurocode 8: Design of structures for earthquake resistance. Part 1:General rules, seismic actions and rules for buildings, British Standards Institution[S]. London,EC8, EN1998-1:2004,

[13] JTG/TB 02-01—2008. 公路桥梁抗震设计细则[S]. 北京：人民交通出版社，2008.

[14] Foss K A. Coordinates which uncouple the equation of motion of damped linear dynamic systems[J]. J Appl Mech, 1958(25): 3610364.

[15] 李创第,黄天立,李暾，等. 带TMD结构随机地震响应分析的复模态法[J]. 振动与冲击，2003,22(1)：36-39.

LI Chuang-di, HUANG Tian-li,LI Tun,et al. The complex modal methods for analysis of random earthquake response of structures with TMD[J].Journal of Vibration and Shock,2003,22(1)：36-39.

[16] 欧进萍.王光远.结构随机振动[M]. 北京：高等教育出版社，1995.

[17] 方同.工程随机振动[M]. 北京： 国防工业出版社，1995.

[18] 刘文锋,白志强，隋杰英，等.设防烈度下非比例阻尼结构地震随机响应峰值区间估计方法[J]. 计算力学学报，2009,26(5):670-675.

LIU Wen-feng,BAI Zhi-qiang,SUI Jie-jing, et al. Interval estimation method of random seismic pea response for non-classically dynamic system under earthquake fortification level[J]. Chinese Journal of Computational Mechanics, 2009,26(5):670-675.

[19] 李刚, 耿程东. 地震作用下钢框架最大弹塑性层间变形的概率统计特性[J]. 计算力学学报，2003,20(3):255-260.

LI Gang, GENG Cheng-dong. Probability distribution of the elastoplastic maximum story dirft of steel frames subject to earthquake load[J]. Chinese Journal of Computational Mechanics,2003,20(3):255-260.

基金项目：“十二五”国家科技支撑计划(2011BAJ09B01-01);潍坊学院青年科研基金项目(2011Z16;2009Z13)

收稿日期：2015-08-17修改稿收到日期：2016-01-28

通信作者马克俭 男，院士，教授，博士生导师，1933年生

中图分类号:TU352;TU375.2

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.14.027

Random seismic response of spatial steel-grid box-structure

BAI Zhi-qiang1,2, MA Ke-jian1, LIU Wen-feng3

(1 Spatial Structures Research Center of Guizhou University, Guiyang 550003, China;2 Department of Architectural Engineering, Weifang University, Weifang 261061, China;3 Civil Engineering Department of Qingdao Technical University, Qingdao 266033, China)

Abstract:The differential motion equation of a steel grid box-structure under ground excitation was given. The close form solutions of time domain response and random seismic response were obtained based on the complex mode theory. A formula for the structure reliability was obtained with a hypothesis of probability distribution of extreme value type I and the confidence interval with a specific probability was derived based on the mean value and variance of random seismic response peaks. Taking the Nanjing multi-function exhibition hall as an example, the mean value and variance of random seismic response peaks were calculated. Meanwhile, 14 complex-mode deterministic displacements were calculated under 14 records of seismic wave excitations. The results indicate that the results of the two methods are consistent. The random response analysis method is an effective assistant calculation method in the design of spatial steel-grid box-structure, and based on that,the reliability of structures’ responses can be estimated.

Key words:box-structure; complex mode; analysis of random seismic response; reliability; interval estimation

第一作者 白志强 男，博士生，讲师，1980年生

E-mail:makejian2002@163.com