边坡稳定可靠度分析的新型四阶矩法

周芬+郭奥飞+杜运兴

摘 要：提出了一种边坡稳定可靠度分析的新型四阶矩计算方法.该方法将均匀设计法、径向基神经网络技术和最大熵原理相结合对边坡进行可靠性分析.采用均匀设计法确定粘聚力和内摩擦角的网络训练样本空间，并采用基于有限元的强度折减法计算样本空间中样本所对应的边坡安全系数.利用这些样本及对应的安全系数训练径向基神经网络.利用训练好的神经网络获得满足统计数量要求的边坡安全系数，并计算边坡安全系数前四阶矩.利用最大熵原理得到边坡安全系数的概率密度函数近似表达式、边坡失效概率以及相应的可靠指标.该方法的计算结果与蒙特卡罗法的计算结果对比表明该方法具有较高的精度.

关键词：边坡稳定；均匀设计法；径向基神经网络；最大熵；可靠度；四阶矩

中图分类号：TB83，TM753 文献标识码：A

文章编号：1674-2974（2016）05-0113-07

Abstract：In this study， a new four-order moment method for reliability analysis of slope stability was proposed. The reliability analysis of slope stability was conducted by the combination of the uniform design method， the RBF neural network technique， and the maximum entropy principle. The network training sample space of cohesion and internal friction angle was firstly determined by the uniform design method， and the slope safety factor related to the samples was obtained by the strength reduction method using the finite element analysis. The RBF neural network was trained by the samples and their corresponding safety factors. The safety factors of the slope satisfying the statistical requirement were obtained by the well-trained neural network， and the first four-order moments of the slope safety factor were calculated. Furthermore， the approximate expression of probability density function of the slope safety factor， the slope failure probability， and the corresponding reliability index were investigated by the maximum entropy principle. Compared with the results from Monte Carlo method， the proposed method shows high precision.

Key words：slope stability； uniform design method； RBF neural network； maximum entropy； reliability； four order moments

边坡稳定性分析方法是岩土工程的一个重要研究内容.边坡稳定分析一般有确定性分析方法和基于概率的不确定性分析方法.杜运兴[[1]和陈昌富[[2]基于确定性分析方法对边坡稳定性进行了研究，通过计算得到边坡安全系数评估边坡的稳定程度.然而由于土体参数的不确定性，在进行边坡稳定分析时，采用基于概率的可靠度分析方法更为合适.目前，在边坡稳定可靠度分析中常用的分析方法有一次二阶矩法[[3-4]、二次二阶矩法[[5]、响应面法[[6-7]、蒙特卡罗法[[8]等分析方法.采用一次二阶矩法、二次二阶矩法对边坡进行可靠度分析时需要在迭代点处对非正态随机变量进行近似当量正态化，同时迭代求解过程较为繁琐；采用响应面法时受响应面函数的形状和试验取样点选取多少的影响较大；当采用蒙特卡罗法进行可靠度分析时，需要数十万次的有限元数值分析，工作量太大.为了克服以上方法所带来的问题，四阶矩法是一个较好的方法.王宇[[9]将四阶矩可靠度分析方法引入到边坡工程可靠度分析中，提出了边坡工程可靠度分析的最大熵法.左育龙[[10]针对岩土工程的功能函数强非线性且难以显式表达的特点，提出了基于人工神经网络的四阶矩法.以上两种四阶矩方法均利用泰勒级数展开的方法由基本随机变量的前四阶矩求得功能函数的前四阶矩，并借助Pearson系统获得功能函数的更高阶矩.采用以上两种四阶矩方法时计算功能函数前四阶矩的公式较为繁琐并且会遇到隐式功能函数求偏导的问题.本文在这些研究的基础上提出了一种边坡稳定可靠度分析的新四阶矩计算方法.该方法将均匀设计法、神经网络技术和最大熵原理相结合对边坡进行可靠性分析，克服了以上两种四阶矩法所具有的缺点.该方法考虑了基本随机变量的概率分布类型，首先采用均匀设计法确定粘聚力和内摩擦角的网络训练样本空间，并采用基于有限元的强度折减法[[11]确定样本空间中样本对应的边坡安全系数，利用这些样本以及样本对应的安全系数训练径向基神经网络.利用训练好的神经网络获得满足统计数量要求的安全系数，并计算边坡安全系数的前四阶矩.利用最大熵原理得到边坡安全系数的概率密度函数近似表达式、边坡失效概率以及相应的可靠度.虽然均匀设计法、径向基神经网络技术、最大熵方法在可靠度领域均已被采用，然而将该3种方法的结合运用尚属首次.

1 边坡稳定可靠度分析

1.1 网络训练样本点的选取

训练神经网络需要一定的样本点作为输入向量，样本点的选取对神经网络的精度、效率尤其重要.样本点的生成方法有中心复合设计法、随机取样法和均匀设计法等.毕卫华[[12]研究了样本点的生成方法对边坡可靠度的影响.该文献认为在相同的精度下均匀设计取样法比中心复合设计法更加有效；在相同的精度下均匀设计法比随机取样法需要生成的样本点少，计算效率高.因此本文采用均匀设计法[[13]进行样本点的选取.具体步骤如下：

1） 将土体参数粘聚力和内摩擦角作为需要考虑的两个因素，确定这两个因素的取值范围，并确定相应因素的样本空间容量，即均匀设计法中的水平数.在相应因素的范围内均匀确定样本的数值；

2）根据样本空间容量选取均匀设计法中相应的使用表和设计表.根据因素数在使用表中确定设计表中所对应的列，设计表每一列的数值为影响因素在其样本空间的位置；

3） 在本研究中因素数为2.将粘聚力和内摩擦角这两个因素按其在样本空间对应的位置获取相应的样本数值并形成训练样本.

1.2 径向基神经网络的建立

根据选取的样本点，采用基于有限元的强度折减方法[[11]计算这些样本点所对应的边坡稳定安全系数.利用样本点和样本点对应的安全系数训练神经网络.本文选用的神经网络是径向基神经网络[[14-15]，这种神经网络采用高斯函数等径向基函数作为神经元传递函数，能够实现非线性关系的映射.径向基神经网络相对于BP神经网络而言往往需要更多的神经元，但是它的训练速度很快.在输入向量样本数目较多的情况下，径向基神经网络的效果是很好的.同时径向基神经网络可以克服BP网络局部极小的缺点.

本文将土体参数{c，φ}作为神经网络的输入向量xi，土体参数{c，φ}对应的安全系数F作为期望输出向量建立径向基神经网络.首先通过激活函数Ri（x）对输入向量xi进行运算，然后对运算结果进行加权求和得到向量yi，，如图1所示.

最后根据得到的yi，和已知的期望输出向量F计算均方误差，当均方误差较大时，需要不断增加中间神经元和个数，直到网络的均方误差满足预先设定的值为止，从而建立一个精度较高的神经网络.

1.3 边坡安全系数前四阶矩计算

利用以上建立的径向基神经网络便可以获得任意一组土体参数{c，φ}所对应的安全系数F.按照统计要求的数量形成安全系数的样本空间.根据此样本空间便可以计算边坡安全系数的前四阶中心矩，具体步骤如下：

1）采用舍选法生成服从一定概率密度函数的粘聚力c和内摩擦角φ随机数.本文采用的舍选法[[16]按照如下步骤确定随机数.

①确定随机数的产生区间[a，b]及概率密度函数为fx（x）.

②确定概率密度函数的上确界f0.

2 算例分析

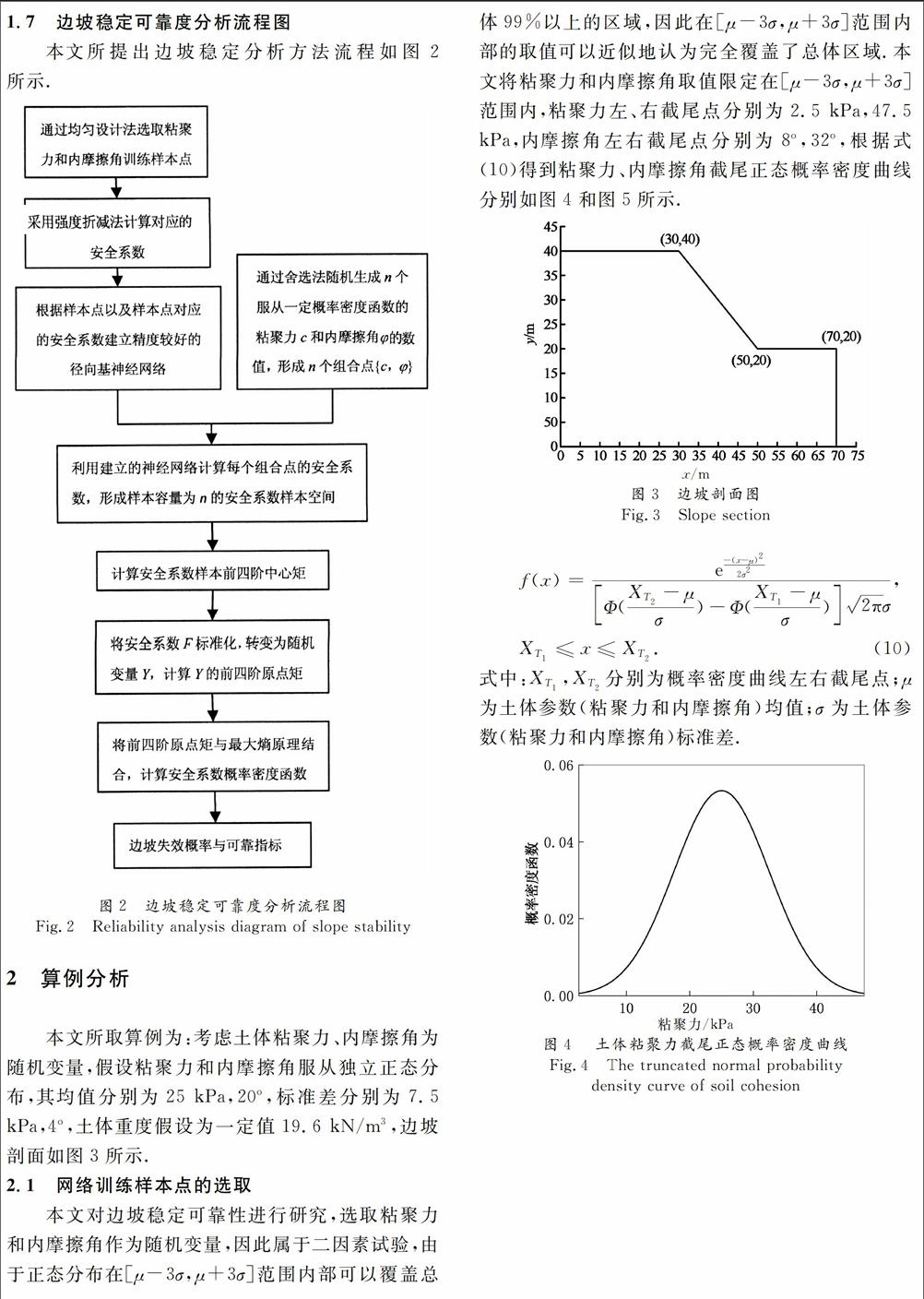
本文所取算例为：考虑土体粘聚力、内摩擦角为随机变量，假设粘聚力和内摩擦角服从独立正态分布，其均值分别为25 kPa，20o，标准差分别为7.5 kPa，4o，土体重度假设为一定值19.6 kN/m3，边坡剖面如图3所示.

2.1 网络训练样本点的选取

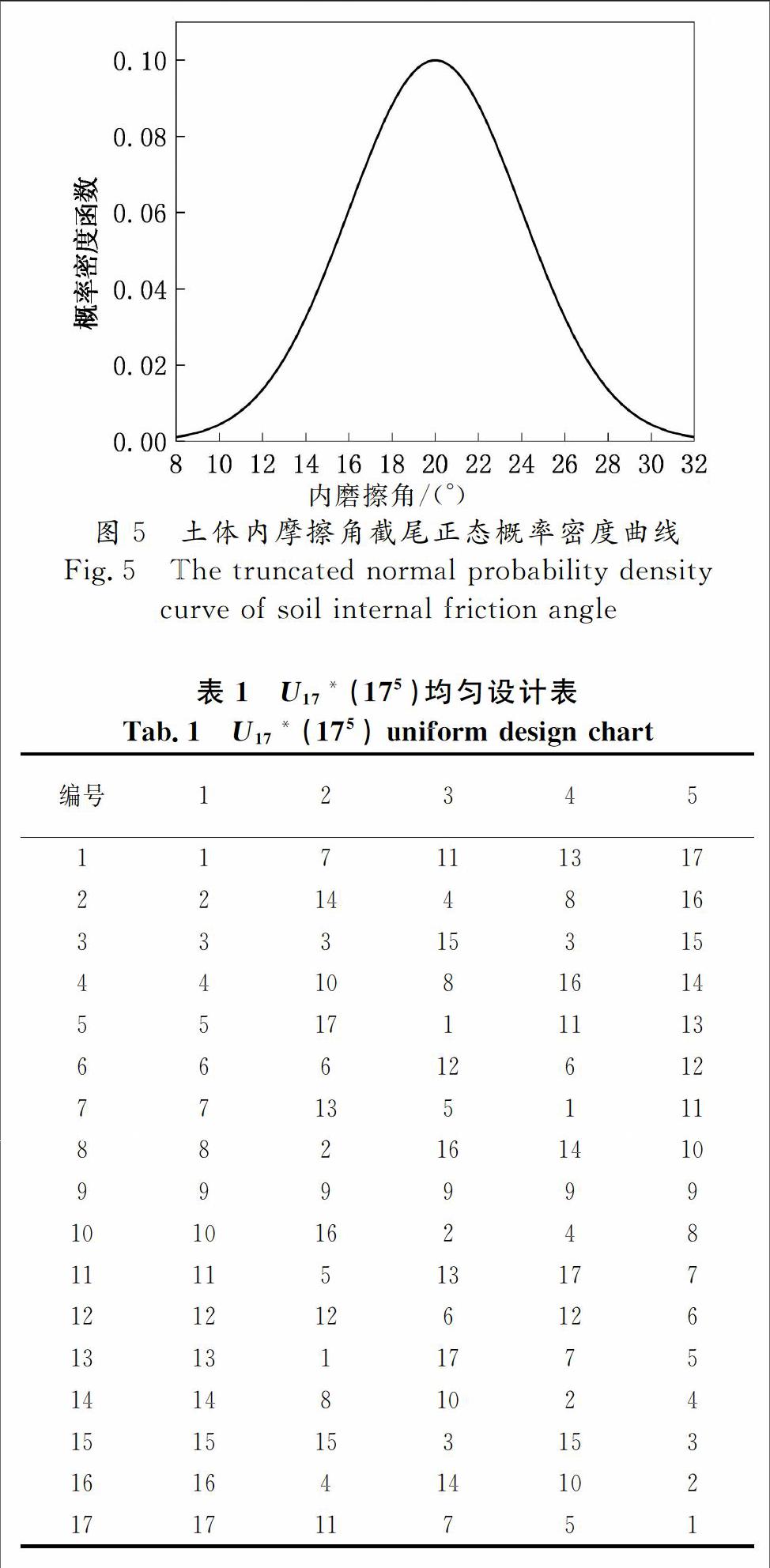
本文对边坡稳定可靠性进行研究，选取粘聚力和内摩擦角作为随机变量，因此属于二因素试验，由于正态分布在[μ-3σ，μ+3σ]范围内部可以覆盖总体99%以上的区域，因此在[μ-3σ，μ+3σ]范围内部的取值可以近似地认为完全覆盖了总体区域.本文将粘聚力和内摩擦角取值限定在[μ-3σ，μ+3σ]范围内，粘聚力左、右截尾点分别为2.5 kPa，47.5 kPa，内摩擦角左右截尾点分别为8o，32o，根据式（10）得到粘聚力、内摩擦角截尾正态概率密度曲线分别如图4和图5所示.x/m

本文将神经网络训练样本空间容量定为17，即粘聚力和内摩擦角水平数均为17，粘聚力样本数值为（2.5， 5.3 125， 8.125， 10.937 5， 13.75， 16.562 5， 19.375， 22.187 5， 25， 27.812 5， 30.625， 33.437 5， 36.25， 39.062 5， 41.875， 44.687 5， 47.5），单位为kPa；内摩擦角样本数值为（8.0，9.5， 11.0， 12.5， 14.0， 15.5， 17.0， 18.5， 20.0， 21.5， 23.0， 24.5， 26.0， 27.5， 29.0， 30.5， 32.0），单位为（°）.根据均匀设计法选取具有17个水平数的均匀设计表和使用表，如表1和表2所示.

根据表2确定两因素设计应当选择表1的第一，二列，表1中的每一列的数值为影响因素在其样本空间的位置，如表3第一、二列所示.本文根据均匀设计法选取的粘聚力和内摩擦角训练样本点如表3第三列所示，本算例选用基于有限元的强度拆减法计算这些样本点对应的安全系数，计算结果如表3第四列所示.将粘聚力和内摩擦角训练样本点绘制在平面图上，如图6所示，可以清楚看到利用均匀设计法选取的样本点分布比较均匀，能够较好地展现总体性质.

2.2 建立径向基神经网络

根据1.2所述方法建立径向基神经网络.为了验证所建立的径向基神经网络的良好性，本文将在粘聚力和内摩擦角取值范围内均匀选取9个验证样本点，分别利用训练好的神经网络、边坡稳定分析软件计算这些验证样本点的安全系数，如图7所示，可以清楚观察到径向基神经网络对隐式功能函数近似效果良好.

2.3 边坡安全系数前四阶中心矩计算并对数据进行处理

采用1.3所述方法得到一个样本容量为n的安全系数样本空间.当n的数目足够多时可以近似总体，可以根据统计学知识比较精确地得到安全系数样本的各阶矩，然而n的数目太大时会对计算效率有一定影响.因此本文通过研究n的变化对边坡可靠度的影响，建议n取1×105～1×106之间的数值.根据式（1）～式（3）计算安全系数F样本的均值、标准差、前四阶中心矩以及偏度系数、峰度系数，结果如表4所示.根据式（6）计算边坡安全系数F的标准随机变量Y的前四阶原点矩，结果如表5所示.

偏度系数是描述分布偏离对称性程度的一个特征数.当分布左右对称时，偏度系数为0；当偏度系数大于0时，该分布右偏；当偏度系数小于0时，该分布左偏.峰度系数是用来度量数据在中心的聚集程度.对于正态分布，峰度系数为3；峰度系数大于3说明观察量更加集中，有比正态分布更短的尾部；峰度系数小于3说明观察量不那么集中，有比正态分布更长的尾部.通过对表4与表5中偏度系数和峰度系数的观察，该算例边坡安全系数概率密度分布并非对称，而是稍微有点右偏，相比于正态分布而言分布较为集中.

2.4 边坡安全系数概率密度函数

当求得边坡安全系数F的标准随机变量Y的前四阶原点矩后，根据式（7），（8）可以得到安全系数的概率密度函数表达式式（11），安全系数的概率密度函数曲线如图8所示.

2.5 边坡失效概率

利用式（9）可以得到边坡的失效概率，然后根据失效概率计算可靠指标.将计算结果与蒙特卡罗法计算结果进行比较，可发现两个方法得到的结果较为吻合（见表6），说明本文所述方法精度较为良好.

3 结 论

建立了一套边坡稳定可靠度分析的新型四阶距方法，该方法具有如下优势：

1）采用强度折减法确定边坡的安全系数，该方法考虑了土体中的应力、应变的分布及变化，概念清晰，鲁棒性较好.

2）提出的方法兼备了均匀设计法、径向基神经网络技术、最大熵原理的优点.均匀设计法具有在相同精度下需要较少的样本点同时精度较高的优点；径向基神经网络技术具有训练速度快同时又能克服BP神经网络局部极小缺点的优点；最大熵原理具有仅根据样本的前几阶矩就能得到样本概率密度函数的优点.

3）提出的方法不需要求取功能函数的偏导数，克服了传统可靠度分析方法不能精确计算功能函数偏导数、工作量大的缺点，能更加简便地进行边坡稳定可靠度分析且精度良好.

将本文方法计算得到的边坡可靠指标与蒙特卡罗法计算结果进行对比，两者结果吻合较好，表明本文所述方法精度良好，具有一定可行性.

参考文献

[1] 杜运兴，尚守平，周芬. 基于遗传算法的边坡稳定有限元分析[J]. 湖南大学学报：自然科学版，2006，33（6）：29-32.

[2] 陈昌富，杨宇. 边坡稳定性分析水平条分法及其进化计算[J]. 湖南大学学报：自然科学版，2004，31（3）：72-75.

[3] CHOWDHURY R N， XU D W. Rational polynomial technique in lope-Reliability analysis[J]. Journal of Geotechnical Engineering， 1993， 119（12）： 1910-1928.

[4] 苏永华，赵明华，张月英，等.利用差分法计算基于Spencer分析模式的边坡稳定可靠度[J]. 岩石力学与工程学报，2006，S1：2751-2756.

[5] BREITUNG K. Asymptotic approximations for multinormalintegrals[J]. Journal of Engineering Mechanics， 1984， 110（3）： 357-366.

[6] WONG F S. Slope reliability and response surface method[J]. Journal of Geotechnical Engineering， 1985， 111（1）： 32-53.

[7] ZHENG Y， DAS P K. Improved response surface method and its application to stiffened plate reliability analysis[J]. Engineering Structures， 2000， 22（5）： 544-551.

[8] HUSEIN MALKAWI A I， HASSAN W F， ABDULLA F A. Uncertainty and reliability analysis applied to slope stability[J]. Structural Safety， 2000， 22（2）： 161-187.

[9] 王宇，张慧，贾志刚. 边坡工程可靠性分析的最大熵方法[J].工程地质学报，2012，20（1）：51-57.

[10]左育龙， 朱合华， 李晓军. 岩土工程可靠度分析的神经网络四阶矩法[J]. 岩土力学， 2013， 34（2）： 513-519.

[11]ZIENKIEWICZ O C， HUMPHESON C， LEWIS R W. Associated and non-associated visco-plasticity and plasticity in soil mechanics[J]. Geotechnique， 1975， 25（4）： 671-689.

[12]毕卫华， 谭晓慧， 侯晓亮， 等. 基于 RBF神经网络的边坡稳定可靠度分析[J].地下空间与工程学报， 2010， 6（2）： 423-428.

[13]方开泰. 均匀设计与均匀设计表[M].北京：科学出版社， 1994：5-46.

[14]朱凯， 王正林. 精通 MATLAB 神经网络[M].北京：电子工业出版社， 2010：225-245.

[15]史峰， 王小川， 郁磊， 等. MATLAB 神经网络 30 个案例分析[M].北京： 北京航空航天大学出版社， 2010：65-72.

[16]张明.结构可靠度分析——方法与程序[M].北京：科学出版社， 2009：89-174.