钢超薄UHPC组合桥面板界面抗剪性能研究
邵旭东+方恒+李文光


摘 要:针对正交异性钢板超薄超高性能混凝土(Ultra High Performance Concrete, UHPC)(厚度为35 mmUHPC板+20 mm磨耗层)组合桥面板中,UHPC层过薄而无法采用常规抗剪连接件形式的问题,提出一种新型钢筋网局部焊接抗剪连接件.通过推出试验测得了焊接抗剪件的荷载滑移关系曲线和抗剪承载力,以某长江大桥为背景,对焊接抗剪件的布置方式进行了研究.试验结果表明:焊接抗剪件的推出试验破坏过程属于脆性破坏,破坏前界面相对滑移较小,焊缝长度为50 mm的焊接抗剪件极限抗剪承载力为119 kN.与栓钉相比,相同荷载比值下采用焊接抗剪件的界面相对滑移小,焊接抗剪件的抗剪刚度大于栓钉.计算结果表明:钢超薄UHPC组合桥面板在布置抗剪件时,需关注UHPC层底部受力.加大抗剪连接件布置密度可减小UHPC层底部横、纵桥向拉应力,降幅可达36.3%.
关键词:桥梁工程;抗剪连接件;推出试验;正交异性钢桥面板;荷载滑移曲线;超高性能混凝土
中图分类号:U443.3 文献标识码:A
文章编号:1674-2974(2016)05-0044-08
Abstract: For the composite bridge deck system composed of orthotropic steel deck and ultra-high-performance concrete (UHPC) layer with 35 mm UHPC plate and 20 mm wearing layer, the UHPC layer is too thin to use conventional shear connectors. Therefore, an innovative shear connectors using the welded rebar mesh was proposed. Load-slip curve and ultimate bearing capacity were evaluated by push-out test. In the background of a Yangtze River Bridge, the optimal lay out of shear connectors was investigated by segmental model of a bridge deck. The test results showed that the brittle failure of the shear connectors occurred, and the ultimate bearing capacity of the shear connector with the 50 mm welded rebar mesh was 119kN. The slippage of the shear connector with the welded rebar mesh was less than that of the stud under the same load ratio. Furthermore, the stress at the bottom of UHPC layer should be considered in the arrangement of the shear connectors. Increased layout density of the shear connectors reduced the transversal and longitudinal tensile stress at the bottom of UHPC layer up to 36.3 %.
Key words:bridge enginnering; shear connectors; push-out test; orthotropic steel deck; load-slip curve; UHPC
正交异性钢桥面由于具有良好的受力性能、较轻的自重,而在国内外广泛应用,但其在轮载的反复作用下易产生两类病害,即钢结构的疲劳开裂和铺装层开裂、脱空[[1-5[],若将超高性能混凝土(Ultra High Performance Concrete,UHPC)与正交异性钢板组合形成组合桥面板,则有望解决这两类病害[[6-7].由于目前大跨径钢桥桥面铺装层厚度普遍在35~80 mm之间[[8],因此组合桥面板中UHPC层厚度亦处于此范围中.本文针对UHPC层厚度仅为35 mm的钢超薄UHPC组合桥面板,做抗剪连接件的研究.
在常规的钢混凝土组合结构中,常用的抗剪连接件为栓钉、PBL剪力连接件等[[9-11[].对于钢超薄UHPC组合桥面板,其UHPC层的厚度仅为35 mm,而现行规范规定栓钉最小长度为40 mm[[12[],同时因其他常用的抗剪连接件形式会对钢纤维分布造成影响亦无法采用.得益于钢纤维的掺入,钢筋与UHPC的粘结力较普通混凝土有很大的提高[[13[],钢筋难以从混凝土中脱出,故钢筋可作为传递剪力的媒介.基于以上思路,本文提出将纵向钢筋局部焊接在正交异性钢桥面板上,以期发挥抗剪连接件的作用.
为了探究钢筋网局部焊接抗剪件(以下简称“焊接抗剪件”)的受力性能与设计布置方式,本文开展了推出试验,测得了焊接抗剪件荷载滑移曲线和极限承载力,并将其与栓钉抗剪件进行对比.然后在此基础上以某长江大桥为工程背景,通过有限元模型计算分析,研究了钢超薄UHPC组合桥面板中焊接抗剪连接件的布置方式.
1 焊接抗剪件推出试验与有限元分析
1.1 试验模型
试件尺寸设计参考Eurocode 4规范[[14[]中标准推出试件尺寸,整体尺寸如图1(a)所示.中间部分为焊接工字钢,钢板厚度均为14 mm,钢材等级为Q345级.两侧为密配筋UHPC板,钢筋采用HRB400级带肋钢筋,横向钢筋直径10 mm,竖向钢筋直径12 mm,横竖间距均为50 mm.UHPC基体组成成分包括水泥、硅灰、石英砂、高效减水剂和水,钢纤维体积分数为3.5%.模型每侧设置4条焊接抗剪件,焊缝采用手工电弧焊,双面焊接熔透角焊缝,焊接长度为50 mm,坡口角度约为45°,厚度约为6 mm,布置间距横向为150 mm,纵向为200 mm,焊条型号根据规范依钢材等级选用E5015以保证焊缝强度不低于母材.焊接完成后,待焊缝冷却至室温进行外观检查,确认其几何尺寸及防止裂纹等缺陷.焊接抗剪件的具体构造如图1(b)所示,试件共浇筑一组,编号分别为RSC-1,RSC-2和RSC-3.
为了与试验结果进行对比验证,采用ANSYS建立推出试件有限元模型,考虑到对称性且减小计算规模,有限元模型仅取为实际模型的1/4.计算中考虑材料非线性,各材料本构关系如图2所示.其中,钢材、钢筋与焊缝的本构关系采用二折线形式的双线性模型,材料参数依规范取值;UHPC的本构关系亦采用双线性折线,弹性模量为40.7 GPa,轴心抗压强度为90.3 MPa,泊松比为0.2.
模型各组成部分均使用20节点高阶实体单元SOLID95单元模拟,建立分离式钢筋及焊接抗剪件实体,试件有限元模型如图3(a)所示.焊接抗剪件的几何形状由实际情况出发,简化为纵、横向钢筋外包部分,长度与实际尺寸一致为50 mm,焊接抗剪件模拟方案见图3(b).计算分析中不考虑UHPC板与钢筋之间的粘结滑移,在UHPC板与钢板之间使用面面接触单元CONTA174和TARGE170模拟两者的接触非线性,根据规范[[15[]假定工字钢表面为未经处理的干净轧制表面,取摩擦系数为0.35.边界条件与试验保持一致,即约束试件底部节点所有自由度,并在对称面施加对称约束.
1.2 加载方案
试验装置如图4(a)所示,加载仪器采用200 t电液伺服压力试验机,界面相对滑移使用千分表采集,千分表布置在试件顶部与底部如图4(b)所示,同时在UHPC板外侧对应焊接抗剪件位置处以及工字钢隔板处布置电阻应变片,应变采集仪器为TDS-602静态应变测试仪.试件底部与加载装置间铺垫细石英沙以找平,试件顶部设置压力传感器以校核压力机读数,同时还设置了球铰并严格对中试件以免产生偏心压力.
1.3 结果与讨论
表1为试验结果汇总表,图5为两种破坏模式实物照片.
由3个试件的不同破坏形态可知,试件的破坏形态与UHPC和钢筋间的粘结效果有关,400 mm长的钢筋焊接2×50 mm=100 mm长为上限,在此基础上再增加焊接长度,剪切破坏是钢筋与UHPC之间的粘结破坏,焊接长度的增加将不起作用.
图6为焊接抗剪件荷载滑移曲线的实测值与计算值对比,由于加载过程中试件底座出现开裂,因此试验值选用试件顶部4个千分表采集数据的平均值,计算值为有限元模型中相应于千分表布置位置的钢板和UHPC板间界面相对滑移,计算值与试验值总体较为吻合.以RSC-1为例说明其试验过程:当加载至400 kN时,工字钢底部与混凝土板之间首先出现了肉眼可见的细小滑移裂缝,裂缝宽度约0.02 mm;当荷载增加至600 kN时,试件一侧底座开裂.当荷载加至630 kN时,试件两侧均出现大量斜向裂缝,从交界面处由30°~45°角斜向下发展;当荷载加至950 kN时,一侧界面裂缝贯通,试件界面相对滑移发展迅速直至该侧焊缝全部剪断而最终破坏.
图7对比了焊接抗剪件和栓钉的荷载滑移曲线,其纵坐标采用P/PU即荷载与极限荷载的比值,焊接抗剪件荷载滑移曲线取自图6中全部试验数据的平均值,栓钉抗剪件的荷载滑移曲线来自文献[16].文献[16]同时指出栓钉抗剪件因直径、长度、试件形状和混凝土等级的不同,而导致其极限承载力随之变化,但不同情况下的荷载滑移曲线形状是相同的,因此可以使用同一个函数来描述其曲线形状,根据文献[16]简化计算公式如下:
P/PU=S/(0.5+0.97S). (1)
式中: P和PU分别为荷载与极限荷载;S为界面相对滑移值.
由图7可知,在承受相同荷载比值时,栓钉抗剪件的滑移量要高于焊接抗剪件.随着荷载比值的增加,二者之间的差值甚至可以达到十倍以上,表明焊接抗剪件的抗剪刚度更高.
2 焊接抗剪件布置方式的研究
常规钢混凝土组合结构在设计布置抗剪连接件时,仅考虑整体界面纵向剪力作用,以单位长度界面纵向抗剪承载力作为控制因素,在满足界面抗剪承载力的条件下均匀布置抗剪件[[17[].由于钢超薄UHPC组合桥面板的局部效应明显,当采用焊接抗剪件时,可通过同时调整焊接抗剪件焊缝长度与数量的方法以满足界面纵向抗剪承载力需求,为对比不同焊接抗剪件布置方案,本节以某长江大桥为工程背景,通过有限元计算探究不同布置方式对组合桥面板受力的影响.
2.1 某长江大桥的节段有限元模型
某长江大桥钢箱梁梁高3.0 m,梁宽36.3 m,桥面板厚14 mm,底板与斜腹板厚度为10 mm,每3.22 m设一道横隔板,非吊点处隔板厚8 mm,吊点处隔板厚10 mm.U形肋肋厚6 mm,上口宽300 mm,下口宽169 mm,高280 mm,间距600 mm.焊接抗剪件的布置考虑了两种不同方案,其横桥向与纵桥向间距分别为:1)300 mm和400 mm;2)150 mm和200 mm.其中方案1)的布置方式如图8所示.
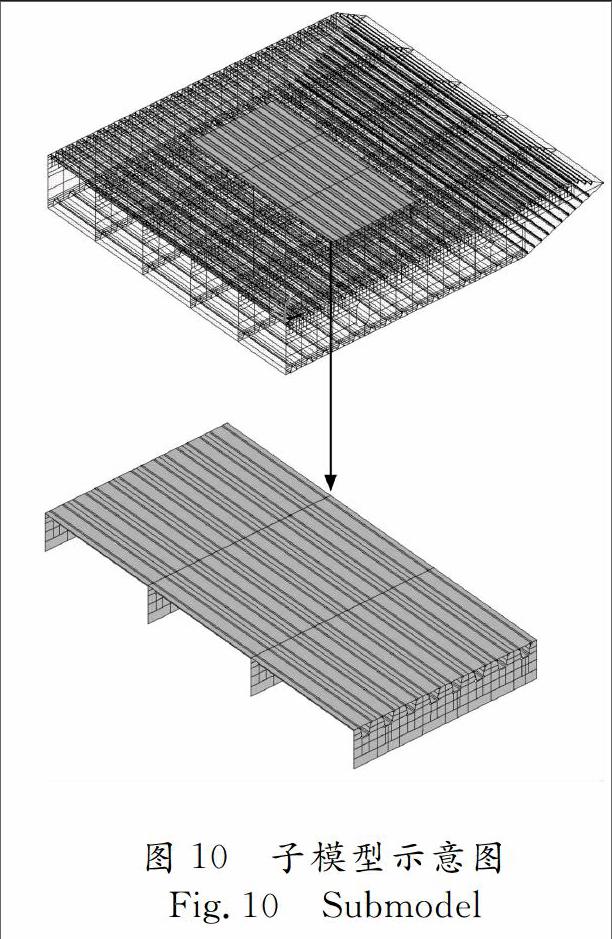
基于ANSYS建立了某长江大桥加劲梁节段模型,纵桥向取两吊点间距即16.1 m,其间计6榀横隔板,横桥向以梁中线为界限取半幅箱梁结构.计算模型中未考虑检修道等附属设施,节段模型如图9所示.为了更精确地获得加载局部范围内桥面板应力分布,采用子模型技术,在局部节段模型中部取一横向8条U肋宽、纵向3跨横隔板间距、高1 000 mm的局部模型作为子模型,如图10所示.子模型所使用的材料参数、单元类型及实常数与节段模型保持一致,单元边长取为20 mm左右.
计算基于线弹性假设,钢板采用4节点壳单元SHELL63单元模拟,弹性模量为206 GPa,泊松比为0.3;UHPC层采用8节点实体单元SOLID45单元模拟,弹性模量为40.7 GPa,泊松比为0.2.
对整体模型,其边界条件为在中心线截面施加对称约束;在模型两端约束沿纵桥向(Y轴)的平动自由度,以及绕横轴(X轴)和竖轴(Z轴)的转动自由度;在吊点位置,约束相应节点竖向(Z轴)自由度.根据圣维南原理及试算结果,边界对计算结果的影响很小.使用整体模型进行计算之后,将子模型边界上的节点号导入,进行位移插值后再将边界条件重新导入子模型,并施加与整体模型相同位置相同大小的荷载,计算并整理得到最终结果.
计算中,假定UHPC层与钢板无拉拔脱层效应,即将UHPC层与钢板交界面处节点的竖向位移进行耦合.而界面抗剪仅考虑了抗剪件的作用,不考虑UHPC层与钢板之间的自然粘结力抗剪,焊接抗剪件使用2节点弹簧单元COMBIN14模拟,抗剪刚度取值根据1.3节中试验值结果,取平均值即1 838 kN/mm,在同一抗剪件位置处设置两个弹簧单元用以分别承担横、纵桥向剪力.界面剪力连接模拟方式如表2所示,除考虑正常布置焊接抗剪件以外,还假定了抗剪件密度为零(即完全滑移)和无穷大(即完全固结)的两种极限情况用以对比.
由于正交异性桥面板应力分布呈现明显的局部性,故可仅考虑单轮作用,根据规范JTG D60-2004《公路桥涵设计通用规范》[[18[]取计算荷载为标准重车后轮轮载,轮重为70 kN,车轮着地面积为200 mm×600 mm(纵桥向×横桥向).参考规范中对汽车冲击力的相关规定,依照文献[18]偏保守地取为汽车荷载局部加载时的冲击系数为1.3.
根据正交异性桥面板的几何构造,横桥向选取正U肋、骑U肋、U肋间3种加载方式,如图11(a)所示.纵桥向从横隔板位置至跨中选取0,1/8,1/4,3/8和1/2跨径处的5处典型截面作为加载位置,如图11(b)所示.
2.2 焊接抗剪件布置方式对UHPC层应力的影响
纵向比较了5处加载位置的应力,结果表明除横隔板截面以外,其余截面在相同加载方式下的应力分布近似相同.横向比较了3种加载方式下的应力,结果表明各加载方式下应力峰值较为接近,其中正U肋加载时峰值略高于U肋间加载和骑U肋加载,因此将跨中正U肋工况作为最不利加载工况,将横隔板正U肋工况作为对比加载工况.
图12为跨中截面正U肋加载时,UHPC层底部与顶部的横、纵桥向应力沿子模型横向分布对比,图13为横隔板截面正U肋加载时,UHPC层底部与顶部的横、纵桥向应力沿子模型横向分布对比,焊接抗剪件布置方案详情及UHPC层应力计算结果见表3,焊接抗剪件剪力计算结果见表4.
通过以上计算结果的对比可知:
1)局部轮载作用下,UHPC层底部横桥向应力大于纵桥向应力,原因是桥面板的纵桥向刚度由于加劲肋的加劲作用而提高,但横桥向由于无加劲构件,刚度较低使得桥面板的横向局部弯曲大于纵向局部弯曲.此外,由于横隔板断面处的U肋中空,故横隔板位置此现象仍然存在.
2)焊接抗剪件的布置方案对抗剪件自身内力峰值有一定影响,当抗剪件布置密度更大,即抗剪件数量更多时,则单个抗剪件分担的剪力较小.与PS-1相比,PS-2中焊接抗剪件的横、纵桥向剪力峰值上更小,对比计算结果与试验结果可知两种方案下,焊接抗剪件自身内力峰值均小于其抗剪承载力.在PS-2中,若拟定焊接抗剪件焊缝长为25 mm,焊缝宽为15 mm,则计算焊缝截面积为25×15=375 mm2.将横桥向剪力峰值4.01 kN与纵桥向剪力峰值3.17 kN相叠加,则单个抗剪件所承受的最大剪力为5.11 kN,最大剪应力为13.63 MPa.由1.3节中试验结果可知,50 mm长焊接抗剪件的抗剪承载力取下限即119 kN.线性内插后得到焊缝长为25 mm的焊接抗剪件的极限抗剪承载力为59.5 kN,极限剪应力为158.67 MPa.局部轮载作用下,焊接抗剪件实际承受的最大剪应力13.63 MPa仅为实际极限强度的8.59%.
3)焊接抗剪件的布置方案对UHPC层底部应力影响较大,而对UHPC层顶部应力影响甚微.与PS-1相比,PS-2中焊接抗剪件沿纵桥向单位长度内的总焊接面积相同,但PS-2中单个焊接抗剪件的规格更小,导致焊接抗剪件横、纵桥向布置间距更小,即布置密度更大.PS-1中UHPC层底部的拉应力峰值为12.65 MPa超过了素UHPC的轴拉强度约为9 MPa,而PS-2中拉应力峰值为8.06 MPa满足要求.以上结果表明,PS-2中焊接抗剪件的布置密度能够确保UHPC层与钢面板之间牢固的组合作用,对UHPC层受力更为有利.
3 结 语
通过本文的研究可以得到以下结论:
1)钢筋网局部焊接抗剪连接件解决了钢超薄UHPC组合桥面板由于UHPC层过薄而难以采用常规抗剪件形式的问题,该抗剪件构造形式简单、施工方便.
2)焊接抗剪件的推出试验破坏过程属于脆性破坏,破坏前试件变形较小.根据实验结果取其下限,则50 mm长焊接抗剪件的抗剪承载力为119 kN.相同荷载比值下采用焊接抗剪件的界面相对滑移比栓钉小,即焊接抗剪件的抗剪刚度大于栓钉连接件.
3)钢超薄UHPC组合桥面板抗剪件设计中需要考虑整体和局部荷载效应的叠加,即除考虑整体纵向剪力包络图之外,还需考虑局部荷载下UHPC层的横向受力.理论计算表明,增加抗剪连接件布置密度能够减小UHPC层底部应力集中,并提高组合结构整体受力效率,在设计中应予以考虑.
4)钢筋网局部焊接抗剪连接件作为一种新型的抗剪连接件形式,其抗剪承载力计算公式、抗剪刚度计算公式等研究内容还有待进一步探索.
参考文献
[1] 陈斌,邵旭东,曹君辉.正交异性钢桥面疲劳开裂研究[J].工程力学, 2012, 29(12):170-174.
[2] 王春生,冯亚成.正交异性钢桥面板的疲劳研究综述[J].钢结构,2009(24):10-14.
[3] 祝志文,钱六五.基于有效缺口应力法的正交异性钢桥面板疲劳评价[J].湖南大学学报:自然科学版, 2015,42(9):59-67.
[4] PFEIL M S, BATTISTA R C. Stress concentration in steel bridge orthotropic decks[J]. Journal of Constructional Steel Research, 2005, 61(8):1172-1184.
[5] FBP D J.Overview fatigue phenomenon in orthotropic-bridge decks in the Netherlands[R]. Sacramento: 2004 Orthotropic Bridge Conference, 2004:489-493.
[6] SHAO Xu-dong, YI Dut-ao, HUANG Zheng-yu, et al. Basic performance of the composite deck system composed of orthotropic steel deck and ultrathin RPC layer[J]. Journal of Bridge Engineering, ASCE,2013, 5(18):417-428.
[7] 邵旭东,张哲,刘梦麟,等.正交异性钢-RPC组合桥面板弯拉强度的实验研究[J].湖南大学学报:自然科学版, 2012, 39(10):7-13.
[8] 黄卫.大跨径桥梁钢桥面铺装设计[J].土木工程学报,2007,40(9):65-77.
[9] LIN Zhao-fei, LIU Yu-qing, HE Jun. Behavior of stud connectors under combined shear and tension loads[J]. Engineering Structures, 2014, 81(81):362-376.
[10]HIGASHIYAMA H, YOSHIDA K, INAMOTO K ,et al. Fatigue of headed studs welded with improved ferrules under rotating shear force[J]. Journal of Constructional Steel Research, 2014, 92(1):211-218.
[11]GATTESCO N, GIURIAN E, GUBANA A. Low cycle fatigue test on stud shear connectors[J]. Journal of Structural Engineering, 1997, 123(2):145-150.
[12]GB/T 10433-2002 电弧螺柱焊用圆柱头焊钉[S].北京:人民交通出版社,2002:2-3.
[13]安明喆,张盟.变形钢筋与活性粉末混凝土的粘结性能试验研究[J].中国铁道科学,2007,28(2):50-53.
[14]Eurocode 4: Design of composite steel and concrete structures, part 1-1 general rules and rules for buildings[S]. Brussels: CEN-European Committee for Standardization, 1994.
[15]GB 50017-2003 钢结构设计规范[S].北京:中国建筑工业出版社, 2003:77.
[16]XUE Wei-chen, DING Min, WANG Hua, et al. Static behavior and theoretical model of stud shear connectors[J]. Journal of Bridge Engineering, 2007, 13(6):623-624.
[17]聂建国.钢-混凝土组合结构桥梁[M].北京:人民交通出版社, 2011:68-70.
[18]JTG D60-2004 公路桥涵设计通用规范[S].北京:人民交通出版社, 2004:25-26.

