距离对连续性泄漏声源定位精度的影响研究

龚小月， 李一博， 靳世久， 边　旭

(天津大学 精密测试技术及仪器国家重点实验室，天津　300072)



距离对连续性泄漏声源定位精度的影响研究

龚小月， 李一博， 靳世久， 边旭

(天津大学 精密测试技术及仪器国家重点实验室，天津300072)

摘要：波束形成是一种较成熟的声源定位算法，已被成功应用于大型混凝土等结构的健康检测[1]，但该方法多用于主动检测或对突发性信号的被动检测。波束形成算法将被用于对连续性声信号的被动检测及源定位，利用L型传感器阵列，通过在1 m×1 m×2.5 mm的镁铝合金平板上实施实验，从原理和实验两方面研究阵列与泄漏源之间的距离对基于波束形成算法的声源定位技术定位精度的影响。实验结果将为该技术在实际应用中传感器阵列的布局提供参考数据。

关键词：气体泄漏；波束形成；距离；定位精度

真空密闭舱在工业等领域中的使用是很常见的。当舱体受到损坏时难免发生气体泄漏，轻则导致密闭结构失效，重则造成严重的生命财产损失，因此对泄漏信号的检测及泄漏源的定位就显得尤为重要。为了有效地检测真空密闭结构是否有泄漏产生并及时找到泄漏源，需要对压力舱进行实时检测。

针对真空泄漏的检测，目前普遍采用的是压降法，即当检测到结构体内的气压发生异常变化时，则表明有泄漏产生。但这种方法并不能对泄漏源进行定位，而在某些特殊环境下，这种方法甚至难以检测到泄漏信号[2]，因此该方法起不到保障安全的作用。另一种较常见的是氦质谱检漏法[3]，它依据质谱学原理，利用氦气作为示漏气体进行泄漏检测，其优点是可定量检测泄漏率，且具有稳定的检测能力，检漏分辨率高，测量范围广，特别适用于微小泄漏率的精确检测。但氦质谱检漏法工艺复杂，且只适合做验证性检测，不能实现对泄漏源的定位，也不能实现在线检测。

以上方法都是以气体为介质进行检测，不但不能进行泄漏源定位，还有可能出现误诊断。为了有效利用泄漏信号，本文采取基于声学的检测方法，利用固体传声的稳定性，检测真空密闭舱壳体薄壁结构体内传播的超声波[2]。薄壁上传播的超声波，即所谓的兰姆波，具有传播距离远且更稳定的特性，更有利于进行结构监测和无损检测[4]。

波束形成法(Beam-Forming)是一种较为完善的声学检测算法，它主要使用相控阵并利用延时叠加(Delay-And-Sum, DAS)对信号进行处理。波束形成法在雷达[5]和地震波检测，以及通信卫星上的应用已经很成熟[6]，其应用波束形成的目的，是将一定几何形状排列的多元基阵中各阵元的输出，经过时延、加权、求和等运算处理，来形成预定方向上的指向性[7]。波束形成在信号源定位的应用中出现的还比较少，一般都是针对突发性信号进行声源定位，或者是应用于主动性的损伤检测，而在对连续性泄漏信号源的被动检测及定位的领域更是很少有应用到该算法。在本文前期工作中[8]，已经利用优化了的波束形成法对连续性泄漏声信号进行源定位，并取得了阶段性的成果。在该研究过程中发现，传感器阵列与泄漏源之间的距离会对该定向算法的定向精度造成一定的影响。通过在原理上分析知道，由于衰减和反射回波的存在，当距离增加时，必然导致泄漏信号的信噪比严重下降。本文在其研究基础之上，通过实验研究泄漏源与传感器阵列之间距离R对该算法定向精度的影响。

1波束形成算法定位原理

波束形成算法的基本思想是通过将阵列中各阵元的输出进行加权求和，将阵列波束导向到某一个特定的方向，称该方向为导向矢量，以对期望信号得到最大输出功率的导向位置给出波到达方向估计，基本原理是通过多个阵元信号的直接相干叠加而获得综合输出。

为了有效实现定位，阵型的选择很关键。通过对线型阵列、矩形阵列、圆形阵列、十字型阵列及L型阵列实验结果的对比发现，L型阵列能以最少的传感器数获得最佳的实验效果，同时单次定向用时短，效率高，可以以最小的系统开销满足项目需求，因此本文选用L型阵列。

本文采用如图1所示的8个传感器组成的90°L型阵列，始终以1号传感器作为基准传感器。利用此阵列对泄漏孔处产生的泄漏信号进行采集。在不知道真实来波方向θ的情况下，假设来波方向为θ′，此方向即为导向矢量，如图中所示。按照导向矢量的方向，以1号传感器为基准，将其他阵元信号进行延时，再进行叠加等得到该假设方向下的能量信息。通过不断改变θ′，最终得到能量(P)-角度(θ′)曲线，通过该曲线可得到声源的估计方向。

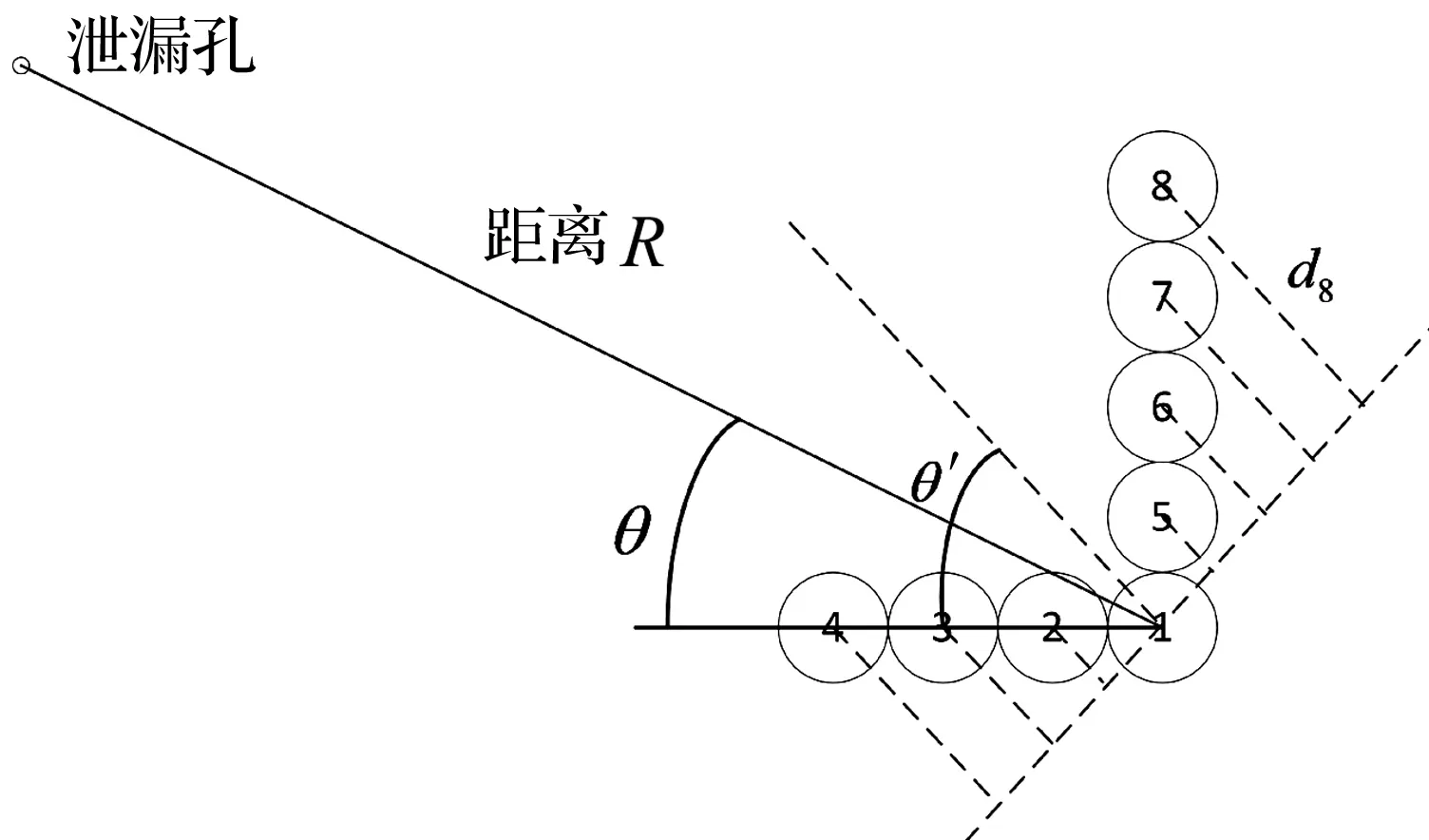
图1　传感器阵列及波束形成法示意图Fig.1 Sketch map of sensor array and beam-forming

图1中R代表阵列与泄漏源的间距，将泄漏源与阵列的相对夹角θ定义为泄漏源实际方向，θ′代表假设方向，根据阵列形状，θ′的取值范围为0°～90°。

根据波束形成原理，在本文的算法中，以1号传感器为基准，将2～8号传感器的信号进行时延，再对这8路的信号进行叠加求能量。假设1～8号传感器接收到的信号分别为

(i=1,…,8)

(1)

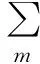
设2～8号传感器与1号传感器到信号源的距离差分别为d2～d8，假设泄漏信号的传播速度为v，则时延

(2)

式中：

di=(i-1)D·cosθ,(i=2,3,4)

(3)

di=(i-4)D·sinθ,(i=5,6,7,8)

(4)

式中：D为相邻两传感器的中心间距。

(i=2,3,…,8)

(5)

对1～8号传感器延时后的信号进行叠加，以此来增强相干信号，减弱非相干信号。叠加信号的能量为

(6)

由式(2)可知，di与定向角度θ′有关，所以式(6)还可以写做如下形式。

P(R,θ′)=α(R)P0(θ′)+P′

(7)

根据波束形成定向原理可知，当θ′=θ时，P应该取最大值，即在P-θ′图(能量-角度分布图)中，峰值对应的位置就是定向结果，如图2所示。

以上是理想距离情况下的计算结果，但实际情况下，由于随着距离的增加导致的信号衰减来自于以及边缘的反射回波，造成信号的信噪比越来越低，从而降低定向精度。当R增大到一定程度时，信号能量衰减，回波影响严重，将会呈现类似图3中所示的情况，即定向结果图的主瓣两边都有旁瓣，同时旁瓣的幅值增大，旁瓣的数量也会增加。

图2　定向结果Fig.2 The result of orientation

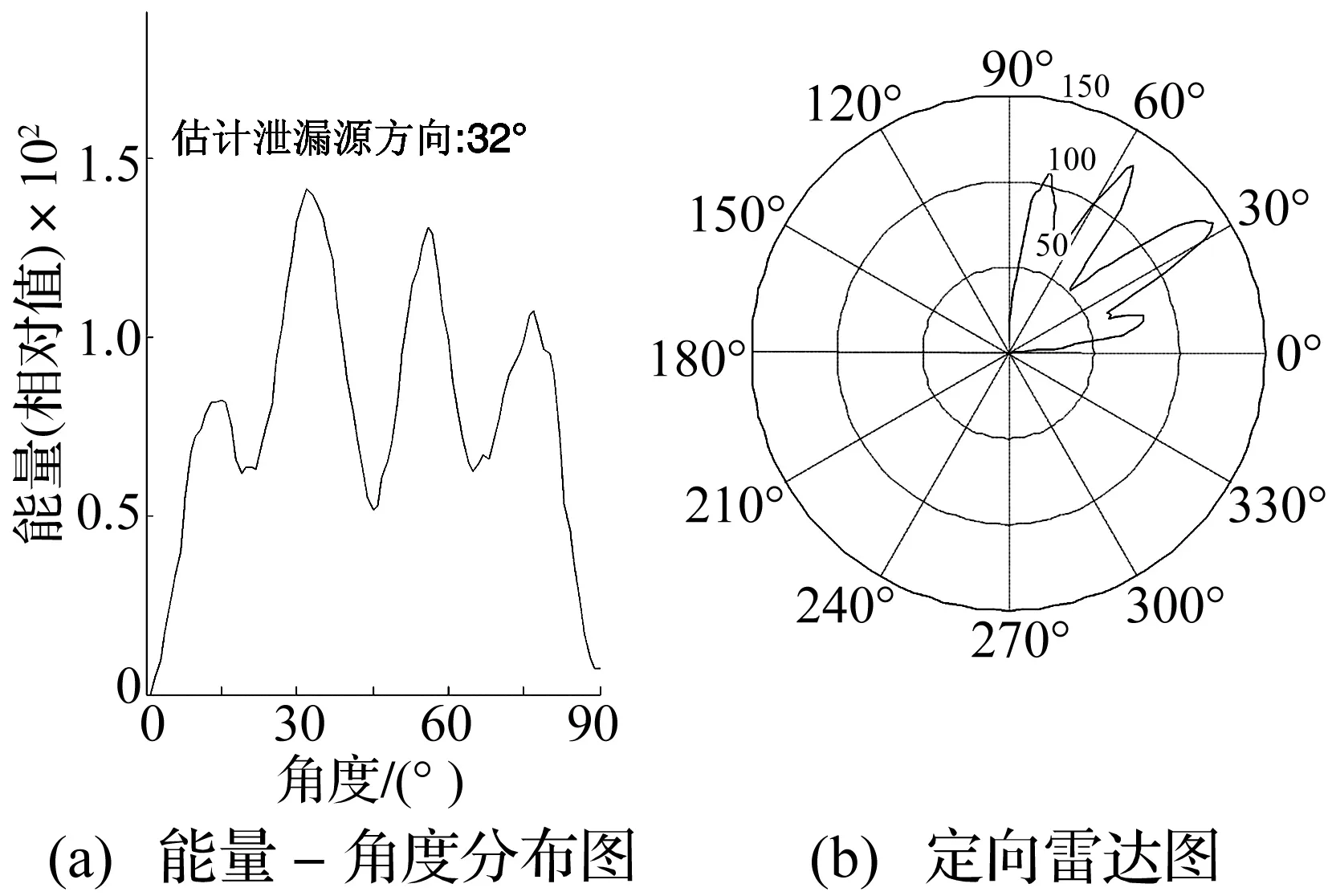
图3　旁瓣增多，幅值增大Fig.3 Increasing sidelobe and amplitude

说明距离R会影响到该定位算法的精度，因此有必要系统地验证R对定向精度的具体影响。

2实验装置

本文的实验系统平台及实物图如图4所示。其中，真空泵通过导气管与置于泄漏孔正下方的气缸相连，开启真空泵，可在气缸内产生低于7 000 Pa的真空条件用于模拟真空环境。图中阴影部分的正方形代表1 m(长)×1 m(宽)×2.5 mm(厚)的铝镁合金板，用于模拟密闭结构壁板，该平板中心位置处有一直径为1 mm的圆形通孔，用来模拟泄漏孔。传感器阵列经过前置放大器(图中标号为1～8)，与声信号采集仪相连，用于采集并记录泄漏信号。计算机一台，用于数据分析及结果显示。

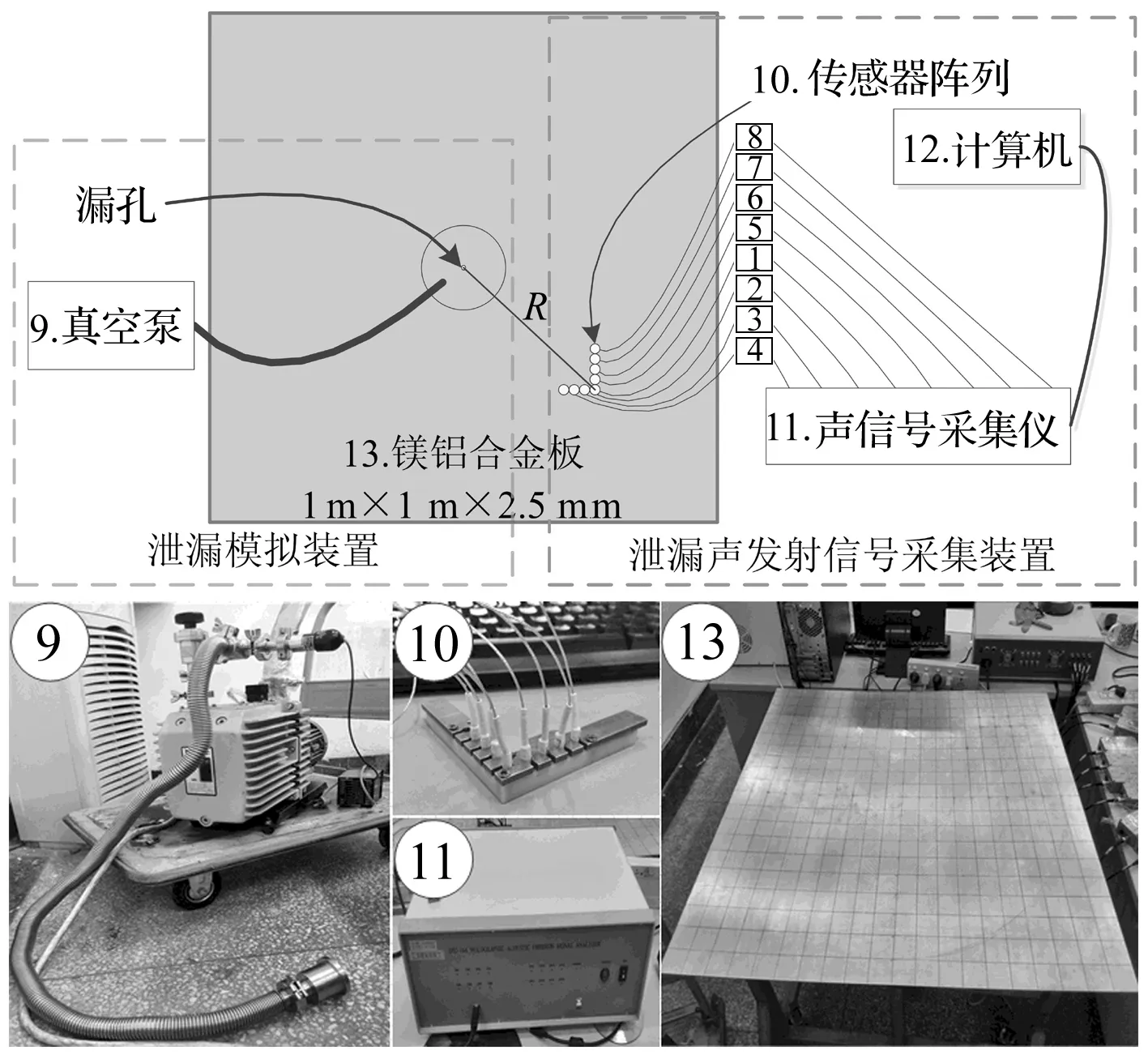
图4　实验平台Fig.4 Experimental platform

根据前期工作结论[9]，试验中的传感器阵列将使用NANO30传感器组成，该传感器直径8 mm；实验时采用的有效频段为100～ 300 kHz，信号的时域图与频谱图如图5所示。

图5　信号时域图与频谱图Fig.5 Time-domain figure and spectrogram

3实验及结果分析

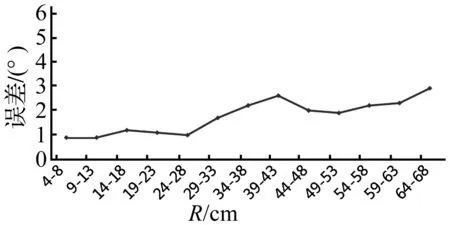
实验时，从R=0 cm开始，以1 cm为间隔逐步移动传感器阵列。为排除泄漏源方向不同对实验结果造成的影响，保证每次的θ为定值，比如令θ≡45°。由于镁铝合金板的尺寸限制，试验中R所能达到的最大值为68 cm。通过10次以上重复实验，得到的统计误差结果分布图如图6所示。为便于统计，以下所说误差均指误差的绝对值。

从图中可以看到，当R<4 cm时，定向误差已经超过10°，不能满足定位要求。这是因为本算法是基于平面波模型进行计算的，根据Mailloux的经验公式[10]，当点泄漏源与传感器阵列之间的距离R满足R≤2L2/λ时为近场模型，应按球面波进行分析；如果R>2L2/λ，则属于远场模型，才可按平面波进行分析，其中L为阵列的最大尺寸，λ为波长。而R<4 cm时则不需要使用仪器进行源定位。

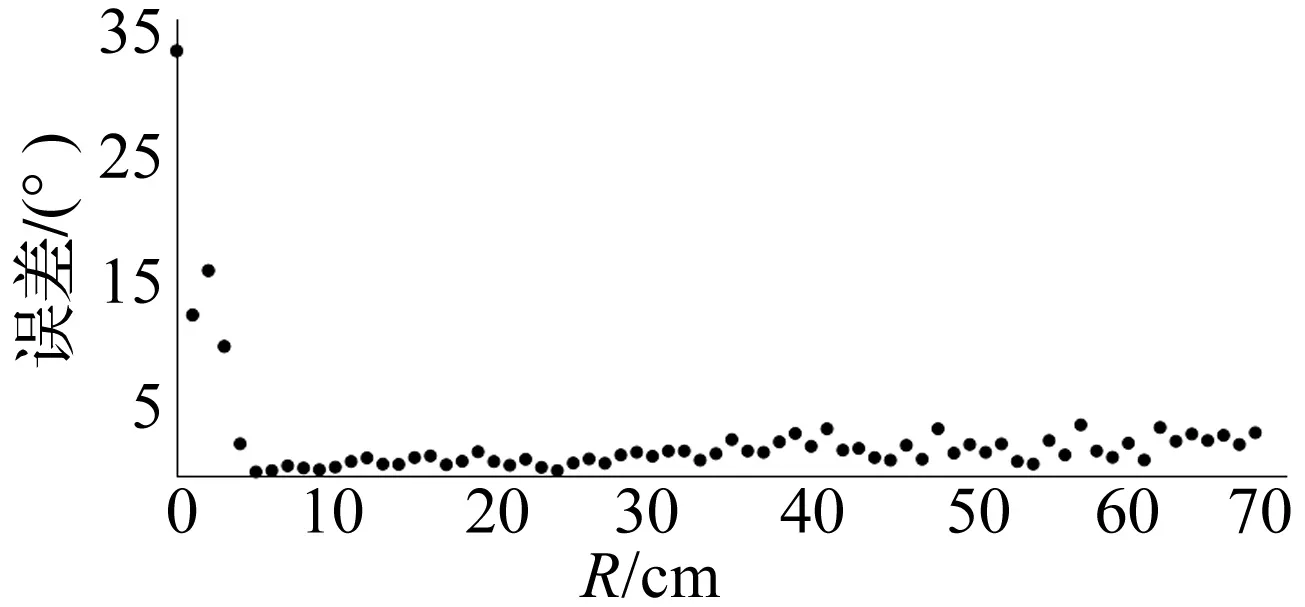
图6　定向误差随传感器阵列与泄漏源距离R的变化Fig.6 The trend of orientation accuracy following by the change of distance between array and the source

由于本算法是基于远场模型，则进行数据分析时不考虑R<4 cm的结果。那么对4 cm≤R≤68 cm的定向误差结果进行观察分析发现，当4 cm≤R≤20 cm时，定向误差有94%都小于2°，只有6%的定向误差大于2°；当20 cm

表1　误差统计

通过计算不同距离段定向误差的平均值，我们得到图7中的结果。

图7　平均误差随距离变化曲线Fig.7 The curves of average error with distance

从图中可以看出，随着距离的增加，平均误差呈现逐渐增加的趋势，即定向误差也有逐渐增加的趋势，说明随着距离的增加，来自于衰减和反射回波的影响会降低该算法的准确性。通过利用Monte-Carlo法及三角测量原理计算得到，当R=60 cm时，5°的定向误差造成的平均定位误差约7.5 cm。更为详细的计算结果如表2所示。

表2　定位误差与定向误差对应表

为了量化测量结果的好坏，规定当平均误差大于5°时，定向误差超过误差许可范围，视为测量失败。根据图6和图7中走线趋势可预估，当R>85 cm时，定向误差可能超过规定的最大误差。

由以上分析说明，该算法的定向误差在4 cm≤R≤68 cm距离范围内能保证定向误差不大于4°，平均定向误差不大于3°，但随着距离的增加，定向误差也呈现增加的趋势。

4结论

通过实验发现，本文中所用到的波束形成算法在1 m(长)×1 m(宽)×2.5 mm(厚)的铝镁合金板上进行对泄漏源定向时，能够得到3°以内的平均误差结果；通过分析实验数据，可预测当泄漏源与传感器之间的距离超过85 cm时，由于信号衰减严重和反射回波的影响带来的信噪比降低，导致定向误差增大，即预测用该算法的定位范围为4～85 cm。在实际应用此方法进行源定位时，该实验结果将为算法优化及传感器阵列的布局提供参考。

此外，对定向误差的数值进行统计发现，在所有的定向误差结果中，有60.3%都为负向误差，而只有14.6%为正向误差。出现这样的现象是否与实验时传感器与泄漏源的相对位置有关，这也将是今后我们研究的一个关键问题之一。

参 考 文 献

[1] McLaskey G C, Glaser S D, Grosse C U. Beamforming array techniques for acoustic emission monitoring of large concrete structures [J]. Journal of Sound and Vibration, 2010,329:2384-2394.

[2] Holland S D, Robert R, Strei M，et al. Two-sensor ultrasonic spacecraft leak detection using structure-borne noise [J]. Acoustical Society of America, 2005, 6(2):63-66.

[3] 孙开磊,孙新利.真空氦质谱检漏原理与方法综述[J]. 真空电子技术, 2007(6): 62-65.

SUN Kai-lei, SUN Xin-li. Summary of the theory and method of vacuum helium-mess-spectroscopy leak detection[J]. Vacuumn Electronics, 2007(6): 62-65.

[4] Engholm M, Stepinski T. Adaptive beamforming for array imaging of plate structures using lamb waves[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2010,57(12):2712-2724.

[5] 朱子平,吕继荣,洪一.数字波束形成在雷达中的应用与分析[J].中国电子科学研究院学报，2006(3): 244-247.

ZHU Zi-ping, LÜ Ji-rong, HONG Yi. Application and analysis of DBF on radar[J]. Journal of CAEIT, 2006(3): 244-247.

[6] 周宇昌.通信卫星星上波束形成技术及发展[J].空间电子技术，2000(3):7-15.

ZHOU Yu-chang. The development of on-star beam-forming technology of communication satellite[J]. Space Electronic Technology, 2000(3): 7-15.

[7] 宋鑫. 时延、相移波束形成技术研究[J]. 信息技术，2005(9):85-87.

SONG Xin. A method of time-delay and phase-shift beam-forming technology[J]. Information Technology,2005(9):85-87.

[8] Bian Xu, Zhang Yu, Li Yi-bo, et al. A new method of using sensor arrays for gas leakage location based on correlation of the time-space domain of continuous ultrasound[J]. Sensors, 2015,15(4): 8266-8283.

[9] 张涛，曾周末，李一博，等. 基于声发射的真空泄漏在线检测技术研究[J]. 振动与冲击，2013,32(24): 164-168.

ZHANG Tao, ZENG Zhou-mo, LI Yi-bo, et al. Vacuum leak detection based on acoustic emission method[J]. Journal of Vibration and Shock, 2013,32(24):164-168.

[10] Mailloux J R. Phased array antenna handbook [M] .Norwood: Artech House Publishers, 2005.

基金项目：国家自然基金项目(61201039)；天津市自然科学基金重点项目(13JCZDJC35400)；天津市自然科学基金一般项目(13JCYBJC18000);天津科技支撑计划项目(14ZCZDGX00003)

收稿日期：2015-05-20修改稿收到日期：2015-07-06

通信作者李一博 男，博士，副教授，1973年6月生

中图分类号:TB517;TB559

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.14.025

Influence of distance on the accuracy of source location of continuous leakage noise

GONG Xiao-yue, LI Yi-bo, JIN Shi-jiu, BIAN Xu

(State Key Laboratory of Precision Measurement Technology and Instrument, Tianjin University, Tianjin 300072, China)

Abstract:The beam-forming method is a mature source location algorithm which is already used in health detection of large concrete structures. However, the method is mostly used in positive detection or sudden signal detection. In the paper, the beam-forming arithmetic was used to passively detect continuous leakage signals, and to locate their sound sources by utilizing an L-shape sensor array to gather the leakage signals. By carrying out experiments on a 1 m×1 m×2.5 mm magnalium plate, the influence of the distance between transducer array and signal source on the accuracy of source location of continuous leakage signal was studied both theoretically and experimentally. The experimental results could be a reference to the collocation of sensor array in the practical application of the method.

Key words:continuous leak; beam-forming; distance; location accuracy

第一作者 龚小月 女，硕士生，1992年12月生