基于SPH-FEM方法的半球形聚能装药破甲特性研究

张之凡, 李　兵, 王龙侃, 张阿漫

(1.哈尔滨工程大学 船舶工程学院,哈尔滨　150001； 2.中国人民解放军91439部队,辽宁 大连　116041)



基于SPH-FEM方法的半球形聚能装药破甲特性研究

张之凡1, 李兵2, 王龙侃1, 张阿漫1

(1.哈尔滨工程大学 船舶工程学院,哈尔滨150001； 2.中国人民解放军91439部队,辽宁 大连116041)

摘要：为了研究杆式射流的形成及破甲过程，基于SPH-FEM方法建立半球形聚能装药模型，对半球形聚能装药起爆后形成金属射流及射流穿透双壳的过程进行仿真模拟。通过对射流形成过程、速度衰减规律以及壳体破口形成过程进行分析，得到以下结论：在半球形聚能装药的爆轰作用下，药型罩被高压冲击变形继而形成了高速的金属射流；射流头部最大速度可达约4 174 m/s；射流在击穿双壳的过程中会发生断裂形成射流断裂块，第一层壳在被击穿过程中，经历了冲塞、凹陷等过程，第二层壳直接被射流穿透，之后不断地被射流断裂块击穿。整个计算旨在对半球形聚能炸药的工程设计提供参考。

关键词：半球形聚能装药；SPH-FEM方法；射流；破甲

聚能装药[1-5]从起爆到形成高速射流，继而进行破甲的过程是一个极其复杂的物理过程，爆轰波从药型罩顶部掠至尾部时，将药型罩以很大的速度向轴向挤压，此时药型罩在极大的压力作用下发生塑性流动加速，最后汇成一股具有高速及高能量的金属射流[6-7]，随后金属射流击穿壳板，在壳板中形成高温、高压、高应变率区域，实现侵彻破甲。半球形聚能装药能够形成杆式射流，射流头部速度可达3～5 km/s，不同于其它射流，杆式射流对炸高的敏感程度较低，但是药型罩利用率较高，破甲能力较高，可以用于攻击新型防护装甲、武装直升机和大型水面舰艇等目标，所以本文对半球形聚能装药形成杆式射流和其击穿双壳结构过程进行研究。随着聚能装药被广泛应用于军事以及工程领域，国内外很多专家学者都对聚能射流的形成以及射流对结构的毁伤进行了深入的研究，Molinari[8]采用有限元方法(Finite Eliment Method,FEM)对聚能射流的形成、断裂及穿透靶板过程进行数值模拟；Liu 等[9-10]基于SPH (Smoothed Particle Hydrodynamics) 方法对线性聚能装药射流的形成以及穿透效果进行研究；温万治等[11]基于MOCL (Markon Cell Line) 分界面跟踪算法，采用二维多流体网格法，模拟了锥形罩聚能装药侵彻钢板的全过程；张先锋等[12]利用有限元软件对三种典型聚能射流的成型及侵彻过程进行了数值模拟；李磊等[13]采用SPH算法实现了锥形罩聚能装药射流形成过程的三维数值模拟。然而，以上数值模拟的都是锥形聚能装药的射流形成过程，半球形聚能装药形成的射流宽度较大，对结构的毁伤更大，破甲效果更好，并且SPH方法[6, 14-17]的无网格特性能克服结构大变形引起的网格畸变等困难，这种特性使得它非常适宜对聚能射流形成过程进行模拟分析。因此，本文结合SPH方法和FEM 方法各自的优越性，应用SPH-FEM方法将半球形聚能装药的射流形成过程以及射流击穿双壳结构的过程进行数值仿真，首先采用SPH方法建立半球形聚能装药模型，模拟金属射流的形成过程，并对射流速度进行分析。随后，在此基础上，建立SPH-FEM聚能射流击穿双壳结构模型，进一步研究金属射流对双壳结构的毁伤过程，分析射流头部速度的衰减规律以及两层壳体破口的形成，旨在为相关的工程应用提供参考。

1基本理论

1.1SPH基本方程

考虑材料的本构关系以及人工黏度Πij，得到具有材料强度的流体动力学控制方程的SPH形式如下[6]：

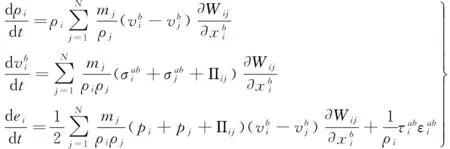
式中：ρ为密度；v为速度；a、b表示坐标方向；p为压力；e为内能；t为时间；x为粒子的位移；Wij为粒子j对粒子i产生影响的光滑函数，本文中所应用的光滑函数为分段三次样条光滑函数[6]；ε为应变率；τ为剪切应力；Πij为人工黏度[6]。

1.2物态方程

(1)爆炸产生的爆轰产物采用Jones-Wilkins-Lee状态方程[18]：

(2)

式中：η为爆炸气体的密度和原始爆炸物的初始密度的比值；ρ0为初始炸药的密度；P为爆轰产物的压力；e0为高能炸药单位质量的内能；A、B、R1、R2为实验数据拟合所得的系数，其具体取值见表1。

表1　TNT爆轰产物Jones-Wilkins-Lee状态方程参数

(2) 药型罩和钢的的状态方程采用固体力学的Mie-Gruneisen状态方程[19-20]

(3)

式中：Γ为Gruneisen常数，pH为冲击Hugoniot曲线上的点的压力，其表达式为[6]：

pH(ρ)=

(4)

表2　金属Mie-Gruneisen状态方程参数

(3) 药型罩和钢的屈服强度采用Johnson-Cook屈服模型[21]：

(5)

表3　金属材料本构模型参数

2聚能射流形成的数值模拟

2.1计算模型

半球形聚能装药结构如图1所示，其中装药采用TNT炸药，炸药高l=0.21 m，半径R=0.08 m，装药中心点起爆；药型罩材料为紫铜，厚度为d=0.004 m。采用不均匀分布的粒子对该模型进行模拟，炸药的粒子间距为dx1=0.001 m，药型罩的粒子间距为dx2=0.002 5 m。

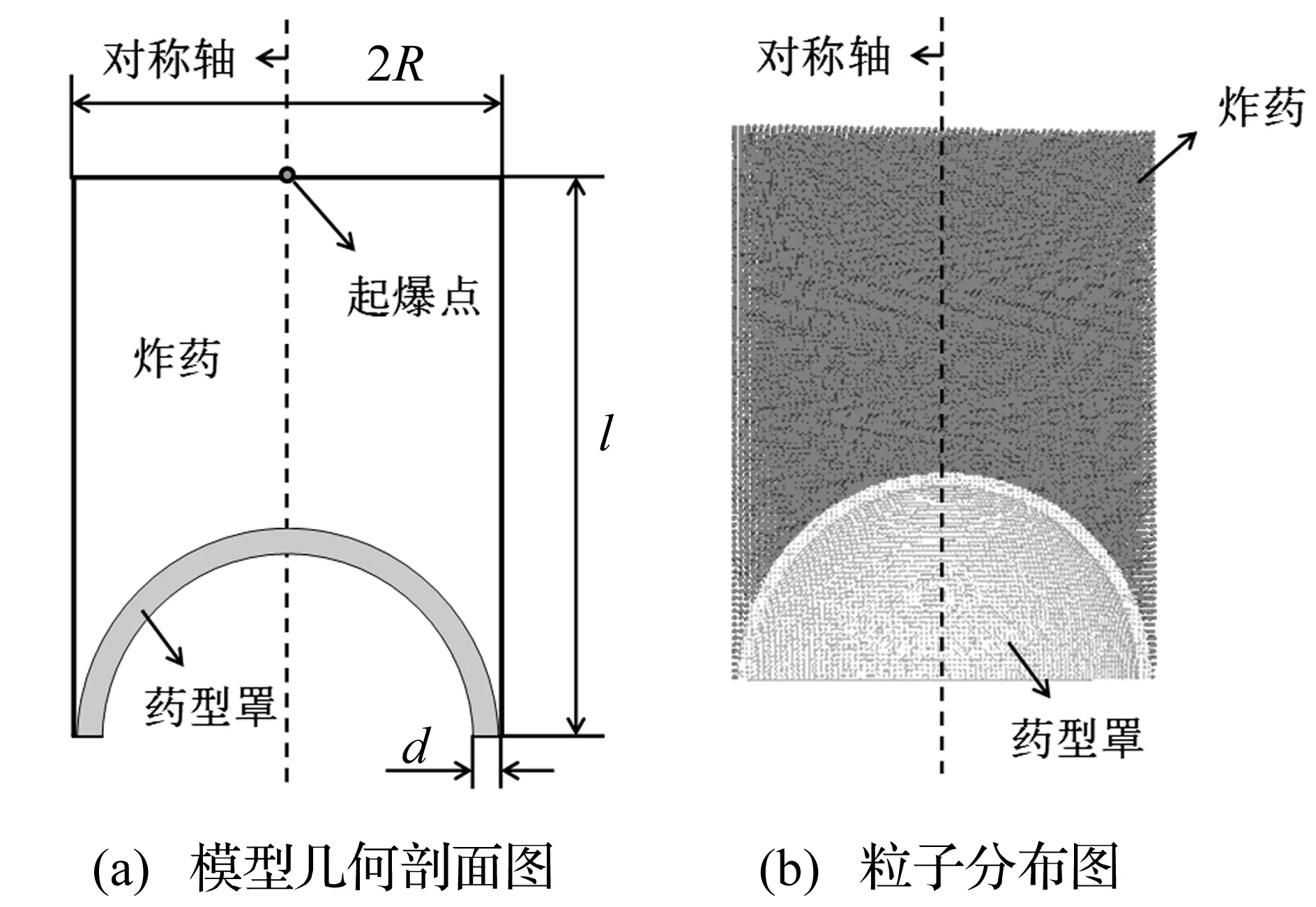
图1　聚能装药计算模型Fig.1 Model of shaped charge

2.2模拟结果及分析

图2为半球形聚能装药射流形成过程及不同时刻的速度云图，初始时刻半球形药型罩如图中t=0时刻所示；t≈48 μs时，在爆轰压力的作用下药型罩的顶部被压垮，并且顶部开始出现外翻，此时头部速度达到约3 281 m/s；t≈54 μs时药型罩继续翻转变形，由于药型罩还受到轴向拉伸和径向压缩，从图中可以看出，整个药形罩向轴线处汇聚并出现拉伸，形成了初始射流，此时头部速度约为3 822 m/s；随着射流的形成，t≈66 μs时药型罩的原内表面渐渐变成外表面，原外表面变成内表面，从图中可以看出，药型罩顶部已经完全被翻转到外面成为射流的头部，此时头部速度达到峰值，约为4 174 m/s，与实验得到的X光照片提供的数据(约4 000 m/s)相吻合[22]；随着金属射流继续向前运动，射流金属拉长变细，头部速度开始减小，t≈84 μs时头部速度约为3 876 m/s，从图中还可以看出射流尾部出现杵；t≈102 μs时尾部杵的长度不断增大，此时射流头部速度继续降低，约为3 821 m/s。由此可得，药型罩在爆轰压力的作用下发生高度变形，同时由于在变形过程中还受到轴向拉伸和径向压缩，药型罩表面激烈变形和碰撞，进而在轴线上聚合形成能量密度更高的聚能射流，且射流头部的速度较高，尾部杵的速度较低，基本上遵循线性的速度分布，符合射流速度分布的基本规律[22]。

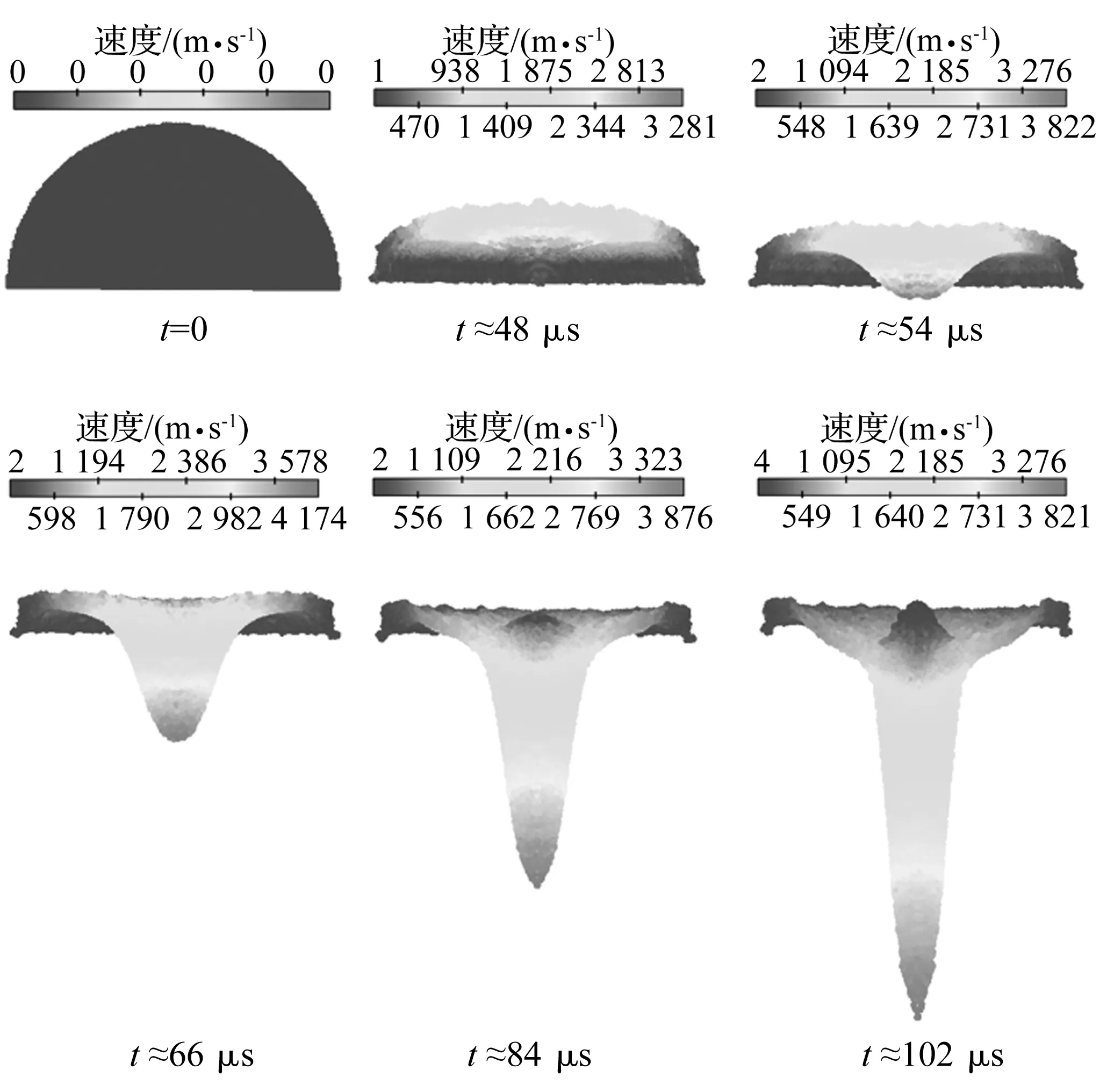
图2　半球形聚能装药射流形成过程(速度云图)Fig.2 Shaped charge jet formation (Velocity contour)

图3为射流头部和尾部的速度时间曲线，图中空心方块为射流尾部的测点A，实心圆圈为射流头部的测点B。从图中可以看出，射流头部和尾部的速度变化趋势相近，都为先增大后减小，整个变化趋势与上图中的速度云图相对应。对于射流尾部，射流末端的粒子具有最大速度值，由测点A的速度曲线可以得到，t≈42 μs时射流尾部的速度达到峰值，约为2 010 m/s，随后速度不断减小，最终趋于稳定。对于射流头部，t≈66 μs时速度达到最大值，约为4 174 m/s，随后速度减小，t≈108 μs时速度趋于平缓，最终头部速度约3 700 m/s。由此可得，射流头部及尾部的速度先增大后减小，头部最大速度可以达到约4 174 m/s，尾部最大速度可以达到约2 010 m/s，与锥形罩相比，射流头部速度较低，但是药型罩利用率较高，射流直径较粗，有利于进一步破甲。

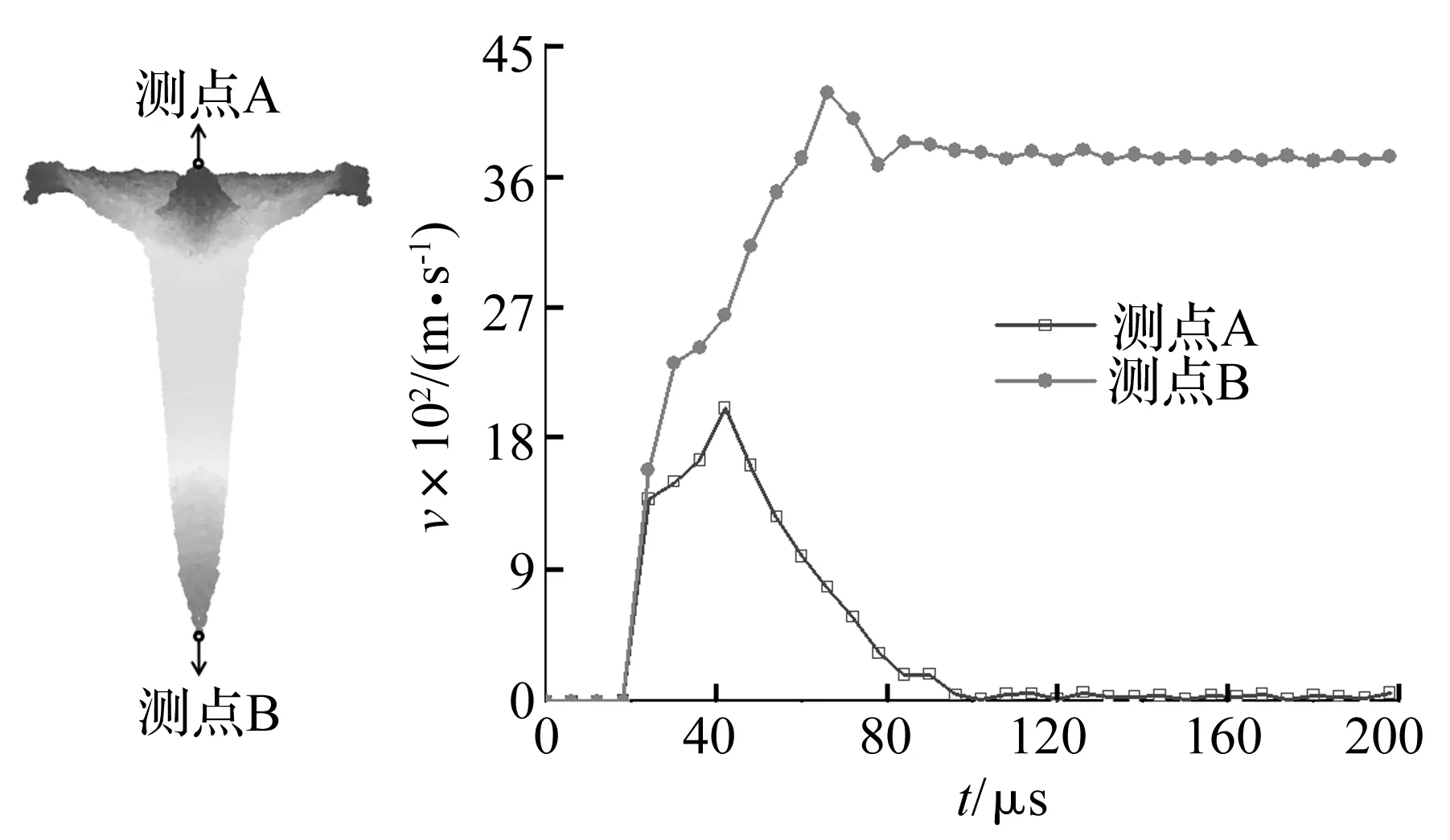
图3　射流头部和尾部的速度时间曲线(测点A和B如左图中标注：A点为射流尾部的测点，B为射流头部的测点)Fig.3 Velocity-time curves of jet head and jet tail (As left figure shows, A and B are test points of jet head and jet tail)

3聚能射流击穿双壳的数值模拟

3.1计算模型

由于结构的对称性，所以本文采用1/2模型进行计算，模型中所用的状态方程及本构关系如1.2节所示，聚能装药采用2.1节中的SPH半球形聚能装药计算模型，两层壳的长和宽皆为a=b=0.5 m，网格单元为四边形单元，网格单元大小为0.002 5 m，对中心区域进行局部画细，局部加密区域长为a1=0.15 m，宽为b1=0.15 m，网格单元大小为0.001 25 m。炸药和药型罩为光滑粒子，壳板为 Lagrange 单元网格，光滑粒子与 Lagrange 单元网格之间采用点到面侵蚀接触算法。炸高h=0.15 m，第一层壳厚为6 mm，第二层壳厚为20 mm，两层壳之间的垂直距离为h′=0.25 m，整个计算模型如图4所示。

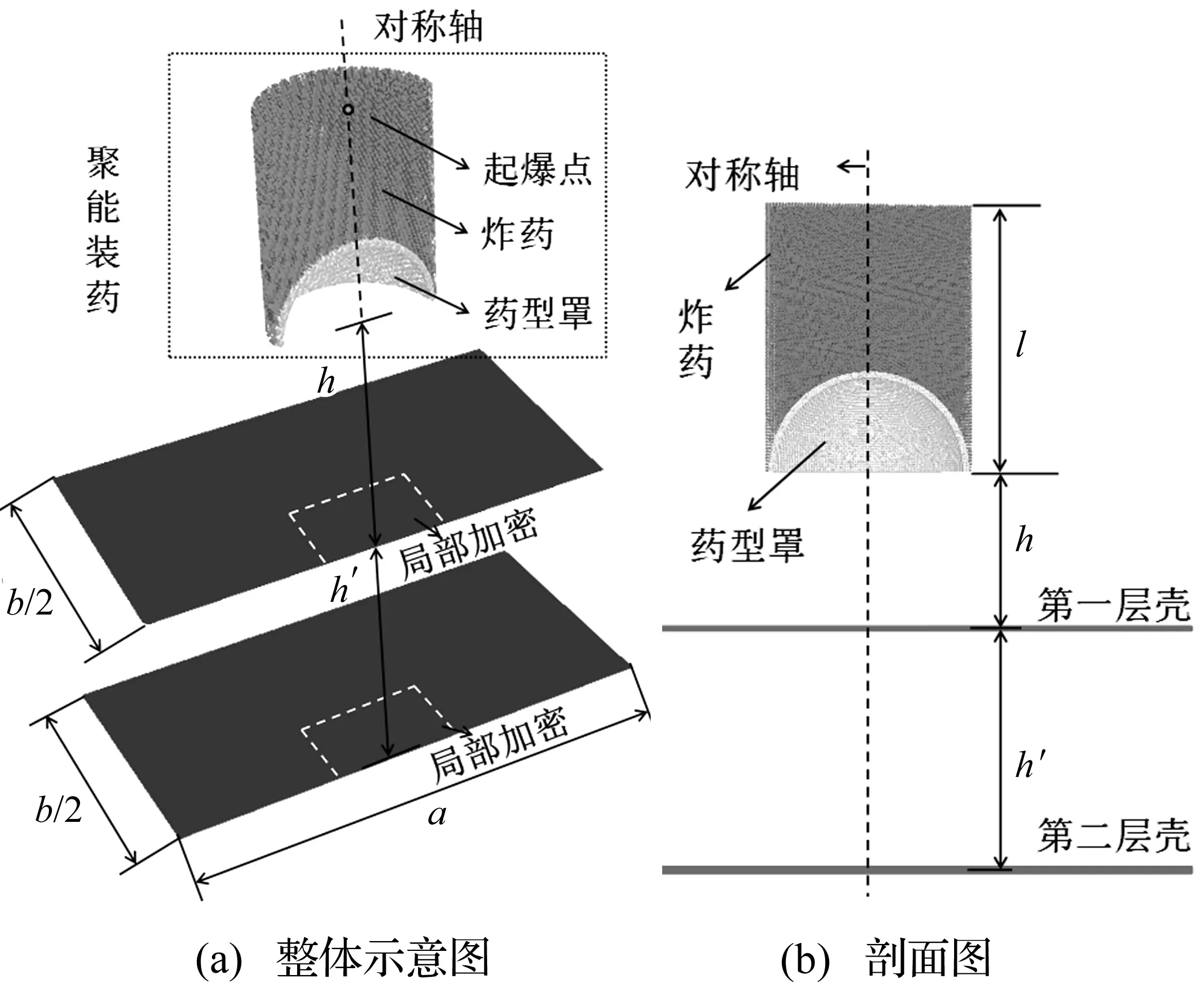
图4　聚能装药作用对结构毁伤的计算模型Fig.4 Model of double-shells subjected to shaped charge

3.2模拟结果及分析

3.2.1射流击穿双层壳的过程

图5为聚能射流的形成及穿透双层壳的过程，聚能装药起爆后爆轰产物会推动半球形药型罩，形成射流弹丸，t≈94 μs时，射流到达第一层壳，随后射流完全击穿第一层壳，由于射流速度很大，射流头部形状没有太大变化，依然保持细长的形状；t≈114 μs时，射流开始断裂，头部出现小块射流；t≈136 μs时射流继续断裂，此时已经断裂成了四块，从图中可以发现，头部断裂的小块射流也在不断被拉长；t≈168 μs，射流开始穿透第二层壳，随后断裂的射流陆续击穿第二层壳，由于第二层壳的阻力作用，射流开始不断的堆积，断裂的射流渐渐融合；t≈240 μs时，射流的主体部分已经穿透第二层壳，由于射流断裂块的堆积，射流主体在击穿第二层壳时发生了“反射”现象，有小部分粒子由于第二层壳的阻力作用而向射流的反方向飞散，从图中还可以看出，已经穿透第二层壳的头部射流金属已经发生飞散，而射流的主要部分由于壳体的阻力作用发生堆积，导致壳体的破口不断增大。整个过程中不仅发生了射流的断裂，还发生了小部分粒子的反射以及穿透之后的飞散现象。

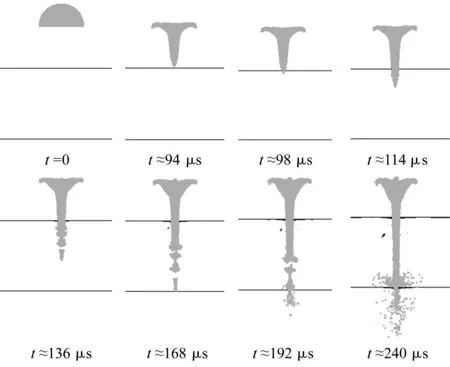
图5　聚能射流击穿双壳的过程Fig.5 Penetration of shaped charge jet onto double-shells

3.2.2射流头部速度衰减规律

图6为射流头部的速度时间曲线，从曲线中可以看出，速度的趋势为先增大后减小，之后又增大最终趋于稳定，最大速度可以达到约4 174 m/s。随着金属射流的形成，头部速度不断增大，t≈66 μs时速度达到最大值，随后速度开始不断减小；t≈94 μs时射流开始击穿第一层壳，从曲线可以明显看出，此时曲线切线斜率增大，这正是由于第一层壳的阻力作用；t≈168 μs时射流开始击穿第二层壳，随后壳的阻力作用以及射流断裂引起速度迅速减小；t≈182 μs时头部断裂部分击穿第二层壳，头部速度达到最小值，约为1 871 m/s，之后，射流头部完全穿透第二层壳，速度开始增大，t≈182 μs后速度趋于稳定，约为2 200 m/s。由此看出，第二层壳的阻力作用对速度衰减的影响较大，其次，射流断裂也对速度减小有一定的影响。

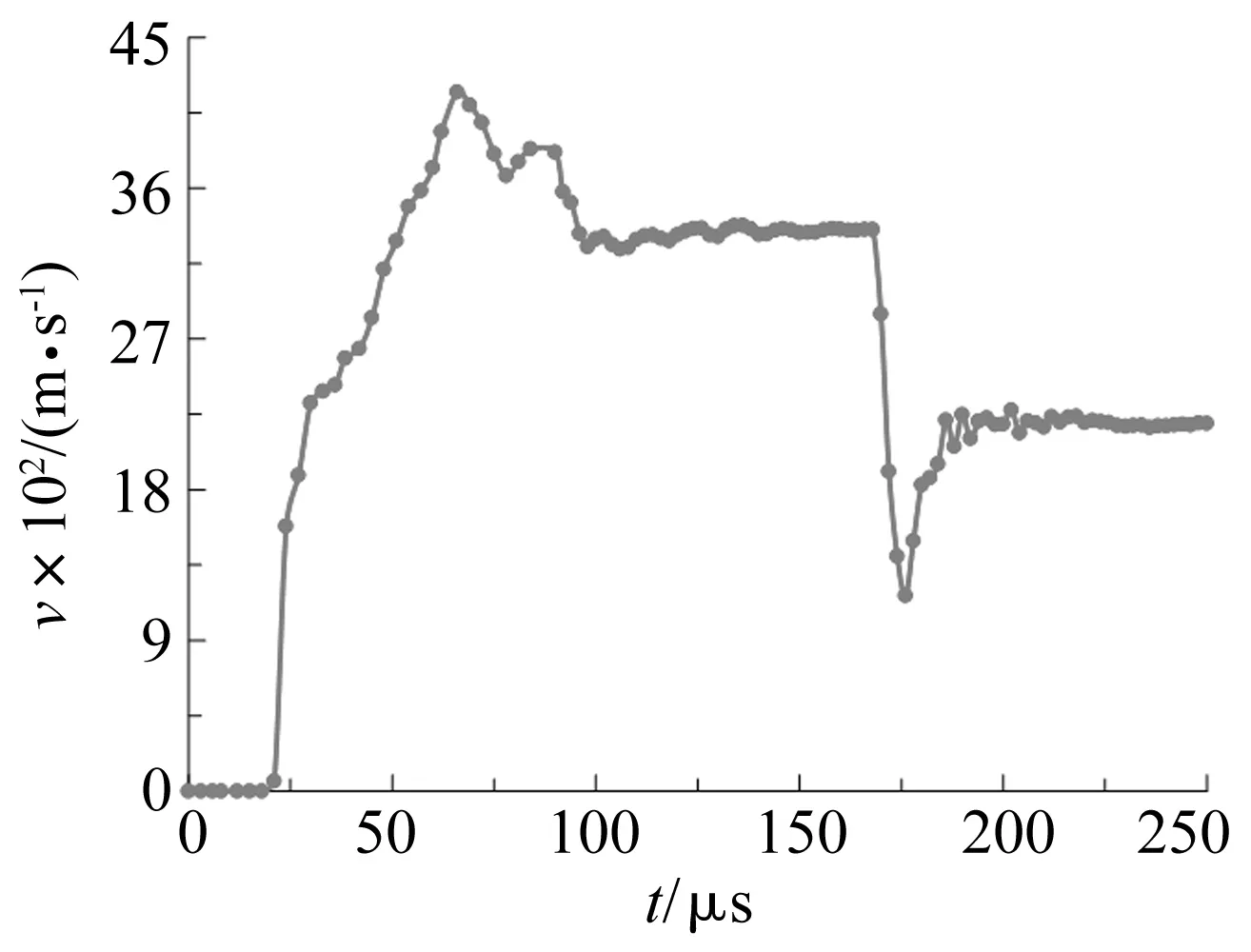
图6　射流头部速度-时间曲线Fig.6 Velocity-time curve of jet head

3.2.3壳体破口形成过程分析

图7为第一层壳Von Mises Stress图，从图中可以看出，聚能装药在起爆后约108 μs时形成的射流已经作用于壳体，此时壳体处于冲塞凹陷阶段，出现大的塑性变形，此时最大应力约达到1.4 GPa；随着聚能载荷的进一步作用，壳体由于塑性变形而变薄；t≈120 μs时表面开始出现破口，此时壳体已经处于凹陷圆盘化阶段，破口的直径约为0.021 4 m，将其与炸药直径进行无量纲化，表示为C，此时C≈0.133；随后壳体被射流完全击穿，壳体中心出现圆形破孔。

图8为第二层壳Von Mises Stress图，从图中可以看出，t≈178 μs时射流头部开始作用于第二层壳，图中初始破口的直径较小，这是由于射流在击穿第一层壳之后出现了断裂现象，射流头部断裂部分首先对第二层壳作用；随后在后续射流断裂块的作用下，壳体直接被击穿，t≈200 μs时C≈0.064 5；随着射流断裂块陆续穿透壳体，射流不断的堆积，断裂的射流渐渐融合，导致破口不断增大，且破口形状不再规则，t≈254 μs时C≈0.136。由此可得，第一层壳在被击穿过程中，经历了冲塞、凹陷等过程，第二层壳直接被射流击穿，之后不断的被射流断裂块击穿。

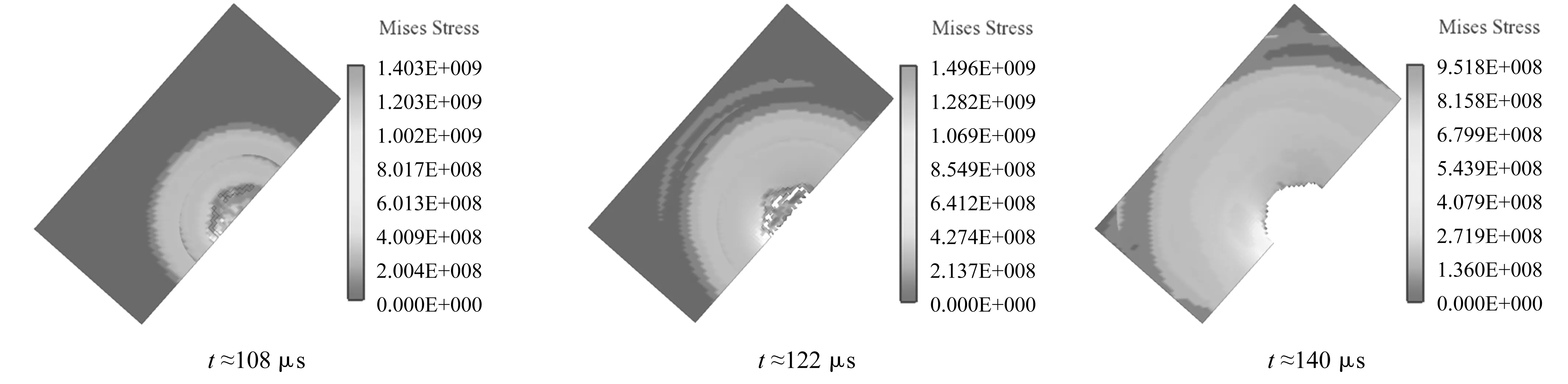
图7　第一层壳Von Mises Stress图Fig.7 Von Mises Stress contour of the first layer of shells

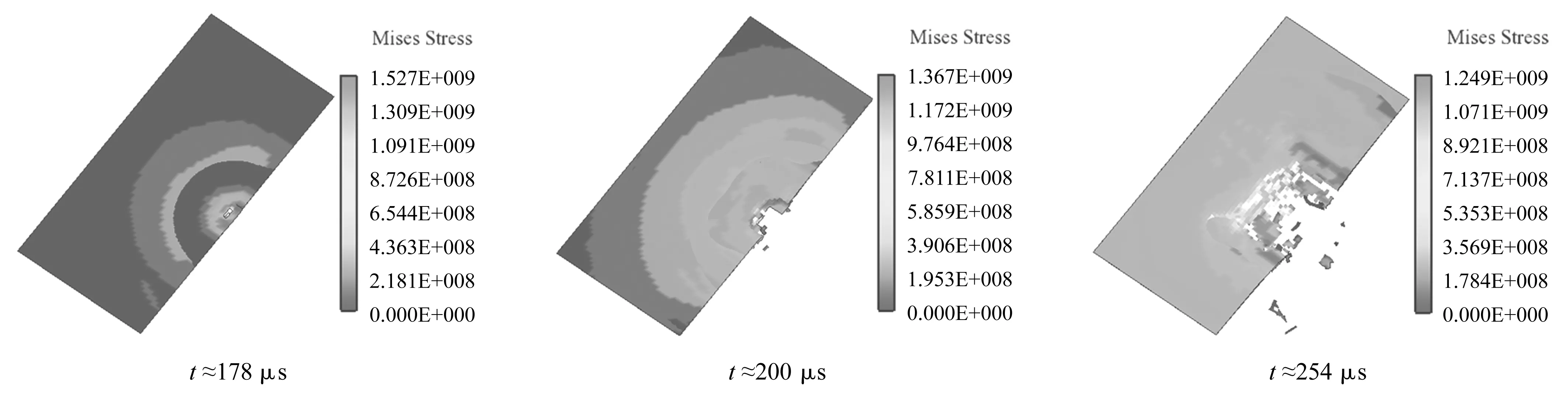
图8　第二层壳Von Mises Stress图Fig.8 Von Mises Stress contour of the second layer of shells

将破口大小与炸药直径进行无量纲化，表示为C，两层壳的破口时间曲线如图9所示，虚线代表第一层壳，从图中可以看出，t≈120 μs时第一层壳出现破口，初始破口与炸药直径无量纲化之后C≈0.133，随着射流载荷的作用，破口越来越大；t≈128 μs时射流完全击穿第一层壳，破口处射流直径基本保持不变，此时C≈0.164，之后破口基本稳定；t≈254 μs时C≈0.174。实线代表第二层壳，从图中可以看出，t≈178 μs时第二层壳出现破口，初始破口与炸药直径无量纲化之后C≈0.054 9，初始破口小于第一层壳的初始破口，这是因为第二层壳首先被射流断裂块击穿；t≈202 μs时后续的射流断裂块作用于壳体，导致破口进一步增大；t≈236 μs射流主体开始击穿第二层壳，且由于射流不断的堆积，断裂的射流渐渐融合，导致破口再一次增大；最后破口大小趋于稳定，t≈254 μs时C≈0.136。由此可得，金属射流在击穿双壳结构的过程中，由于射流断裂导致第二层壳的初始破口小于第一层壳的初始破口，随着射流的进一步作用，破口进一步增大，最终第一层壳的破口约为第二层壳破口的1.3倍。

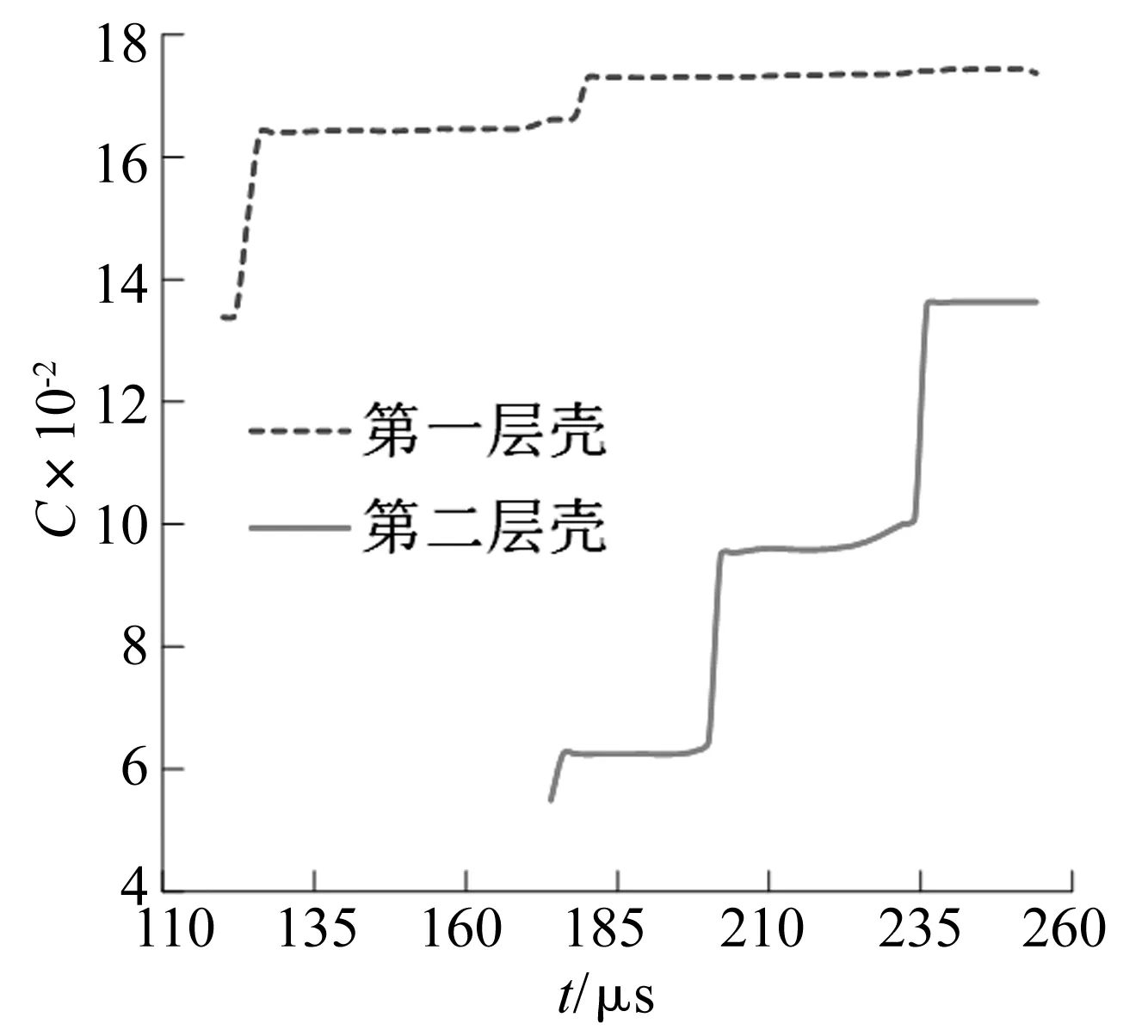
图9　第一层壳和第二层壳的破口-时间曲线(图中C指将破口大小与炸药直径的无量纲化)Fig.9 Crevasse-time curves

4结论

本文首先采用SPH方法建立半球形聚能装药模型，对金属射流的形成进行分析，得到以下结论：药型罩在高压的爆轰压力作用下发生高速变形，并由于受到轴向拉伸和径向压缩，进在轴线上聚合形成聚能射流；射流头部最大速度可以达到约4 174 m/s，尾部最大速度可以达到约2 010 m/s，射流头部的速度较高，尾部杵的速度较低，基本上遵循线性的速度分布，符合射流速度分布的基本规律。在此基础上，建立SPH-FEM半球形聚能装药击穿双层壳模型，对射流速度以及毁伤过程进行分析，得到以下结论：

(1) 射流头部速度先增大后减小，在击穿第二层壳以后速度有所增大但最终趋于稳定，头部最大速度可以达到约4 174 m/s，第二层壳的阻力作用对速度衰减的影响较大；

(2) 第一层壳在被击穿过程中，经历了冲塞、凹陷等过程，第二层壳直接被射流击穿，之后不断的被射流断裂块击穿；

(3) 第一层壳的初始破口大于第二层壳的初始破口，约为2.4倍，这是由于第二层壳先被射流断裂块击穿，随着射流的进一步作用，破口进一步增大，最终第一层壳的破口约为第二层壳破口的1.3倍。

参 考 文 献

[1] 黄正祥, 张先锋, 陈惠武,等. 药型罩锥角对聚能杆式侵彻体成型的影响[J]. 南京理工大学学报, 2005, 29(6): 645-657.

HUANG Zheng-xiang, ZHANG Xian-feng, CHEN Hui-wu, et al.Influence on formed mechanism of jetting projectile charge by liner angle[J]. Journal of Nanjing University of Science and Technology, 2005, 29(6): 645-657.

[2] 曹丽娜. 聚能射流和破甲过程数值模拟方法的研究[D]. 长春: 长春工业大学, 2010.

[3] Perez E, Fauquignon D,Chanteret P. Fundamental studies of shaped charge mechanisms[C]// Proc 3rd Intern Symp on Ballistics. Karlsruhe,Germany, 1977.

[4] 初文华. 处理非连续问题的三维SPH算法及其在冲击动力学问题中的应用[D].哈尔滨:哈尔滨工程大学,2013.

[5] 贾鑫, 黄正祥, 祖旭东,等. 聚能装药垂直侵彻橡胶复合装甲的变形研究[J]. 工程力学, 2013, 30(2): 451-457.

JIA Xin, HUANG Zheng-xiang, ZU Xu-dong, et al. Research on deformation of rubber composite armor against shaped charge vertical penetration[J]. Engineering Mechanics, 2013, 30(2): 451-457.

[6] Liu G R, Liu M B. Smoothed particle hydrodynamics: a meshfree particle method[D]. Singapore:World Scientific Publishing, 2003.

[7] 郑平泰, 杨涛, 秦子增. 聚能射流形成过程的理论建模与分析[J]. 国防科技大学学报, 2006, 28(3): 28-32.

ZHENG Ping-tai, YANG Tao, QIN Zi-zeng. Theoretical modeling and analysis of the formation process of shaped charge jet[J]. Journal of National University of Defense Technology,2006, 28(3): 28-32.

[8] Molinari J F. Finite element simulation of shaped charges[J]. Finite Elements in Analysis and Design,2002,38:921-936.

[9] Feng D L, Liu M B, Li H Q,et al. Smoothed particle hydrodynamics modeling of linear shaped charge with jet formation and penetration effects[J]. Computers & Fluids, 2013, 86: 77-85.

[10] Liu M B, Liu G R, Zong Z,et al. Computer simulation of high explosive explosion using smoothed particle hydrodynamics methodology[J]. Computers & Fluids, 2003, 32: 305-322.

[11] 温万治, 恢寿榕, 赵衡阳,等. 聚能装药侵彻钢板全过程的数值模拟[J]. 爆炸与冲击, 2001, 21(2): 126-130.

WEN Wan-zhi, HUI Shou-rong, ZHAO Heng-yang, et al. Numerical simulation for penetration of a steel slab by a shaped charge[J]. Explosion and Shock Waves, 2001, 21(2): 126-130.

[12] 张先锋, 陈惠武. 三种典型聚能射流侵彻靶板数值模拟[J]. 系统仿真学报, 2007,19(19): 4399-4410.

ZHANG Xian-feng, CHEN Hui-wu. Computional study of three typical shaped charge jets[J]. Journal of System Simulation, 2007,19(19): 4399-4410.

[13] 李磊, 沈兆武, 李学岭,等. SPH方法在聚能装药射流三维数值模拟中的应用[J]. 爆炸与冲击,2012,32(3):316-322.

LI Lei, SHEN Zhao-wu, LI Xue-ling, et al. Application of SPH method to numerical simulation of shaped charge jet[J]. Explosion and Shock Waves, 2012, 32(3): 316-322.

[14] Zhang A M, Yang W S, Yao X L. Numerical simulation of underwater contact explosion[J]. Applied Ocean Research, 2012, 34:10-20.

[15] Zhang A M, Yang W S, Huang C, et al. Numerical simulation of column charge underwater explosion based on SPH and BEM combination[J]. Computers & Fluids, 2013, 71:169-178.

[16] Zhang A M, Ming F R, Wang S P. Coupled SPHS-BEM method for transient fluid-structure interaction and applications in underwater impacts[J]. Applied Ocean Research, 2013, 43: 223-233.

[17] Zhang Z F, Ming F R, Zhang A M.Damage characteristics of coated cylindrical shells subjected to underwater contact explosion[J]. Shock and Vibration, 2014(1):1-15.

[18] Dobratz B M. LLNL Explosive Handbook. UCRL-52997[M]. Livermore, CA: Lawrence Livermore National Laboratory, 1981.

[19] Shin Y S, Lee M, Lam K Y,et al. Modeling mitigation effects of water shield on shock waves [J]. Shock and Vibration, 1998, 5:225-234.

[20] Libersky L D, Randles P W, Carney T C,et al. High strain Lagrangian hydrodynamics: a three-dimensional SPH code for dynamic material response[J]. Journal of Computational Physics, 1993, 109: 67-75.

[21] Johnson G R, Cook W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[C]//Proceedings of the 7th International Symposium on Ballistics.Hauge, Netherlands,1983.

[22] 廖海平. 聚能侵彻体对双层反应装甲的冲击起爆 [D]. 南京:南京理工大学, 2003.

基金项目：国家自然科学基金(U1430236;51479041;51279038)

收稿日期：2015-03-30修改稿收到日期：2015-07-29

通信作者张阿漫 男，教授，博士生导师，1981年3月生

中图分类号:O385

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.14.011

Penetration characteristics of hemispherical shaped charge based on SPH-FEM method

ZHANG Zhi-fan1, LI Bing2, WANG Long-kan1, ZHANG A-man1

(1. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China；2. The 91439th Unit of PLA, Dalian 116041, China)

Abstract:In order to investigate the formation of rod-liked jet and the penetration properties, a SPH-FEM model of hemispherical shaped charge was established to simulate the formation of metal jet and its penetration into double-shells. Through the analysing the formation process of shaped charge jet, the attenuation of velocity and the process of crevasse forming, it is shown that a metal jet with a high speed will be generated after the liner gets deformation under the detonation of shaped charge; the maximum velocity of jet head reaches about 4 174 m/s; during the penetration process of the first layer of shells by the jet, it experiences plug failure, denting, petaling etc. In addition, the jet breakup happens before the jet penetrates the second layer of shells and the initial crevasse occurs. The calculation and analysis presented above may be helpful for designing shaped charges.

Key words:hemispherical shaped charge; SPH-FEM; metal jet; penetration

第一作者 张之凡 女，博士生，1990年1月生