考虑分布鲁棒条件风险价值的供电公司购电组合计划

夏海杰，林士勇（.台州学院物理与电子工程学院，台州 38000；.浙江省乐清市供电公司，乐清 35600）

考虑分布鲁棒条件风险价值的供电公司购电组合计划

夏海杰1，林士勇2
（1.台州学院物理与电子工程学院，台州 318000；2.浙江省乐清市供电公司，乐清 325600）

摘要：考虑多个电力市场售电价格概率分布存在不确定性，在确保供电公司购电损失的分布鲁棒条件风险价值均能满足要求的前提下，以供电公司期望收益最大化为目标，构建了多市场购电组合优化模型。以在实时市场、日前市场和中长期合约市场3个不同市场的购电组合为例，将上述模型转化为半定规划问题进行求解。分析结果表明：所提出的模型与求解办法为供电公司在多能量市场的购电决策提供了新方法。

关键词：分布鲁棒；条件风险价值；半定规划；购电组合

在电力市场环境下，供电公司将作为独立的经营主体，负担着从多个能量市场购电并向终端用户供电的服务。由于政府管制等原因，供电公司在对用户售电时其价格在某段时间段内是固定不变的，因此只有通过调整其在多市场购电策略来平抑风险扩大收益。然而不同市场中的电价由于供求关系、报价策略等条件的影响而具有波动性［1-4］，这些因素直接影响供电公司在不同市场中的购电组合决策。因此，在研究供电公司在多市场中购电组合策略时，需要考虑电价波动的不确定性［5］。

目前的研究中，关于电力市场中的风险管理方法主要分为均值-方差模型和条件风险价值CVaR （conditional value-at-risk）［6-14］两类。文献［6-10］采用均值-方差模型建模分析了供电公司多市场的收益与风险管理问题，均是将电价的方差作为风险。均值-方差模型未能考虑供电公司的风险忍受度，且在计量风险时涉及到投资者的期望收益部分，因此有必要在模型上进一步完善。文献［11-14］将金融领域的风险管理引入供电公司在多市场中的购电组合决策，建立了基于确定概率分布的CVaR购电组合模型。虽然CVaR作为风险度量指标，反映了投资者对风险的偏好程度，所计量出风险值也在一定程度上反映了真实购电损失，但在计算CVaR模型时要求知道准确的电价概率分布，而准确的概率分布信息在实际中往往很难获取。为此，文献［5］使用了加权CVaR模型，在两种概率分布之间通过人为设置权重值来进行概率分布的协调。

然而，以上研究均未考虑在实时市场、日前市场和中长期合约市场中，电价的概率分布存在不确定性的情况。由于不同市场中的历史数据往往会发生变化，长期数据建立的概率分布无法准确反映近期获取的少数数据所代表的实际概率分布，为此，有必要开展针对不同市场中电价数据量少、概率分布不易确定问题的研究。

本文首先通过分布鲁棒条件风险价值DRCVaR （distributional robust conditional value-at-risk）概念引出购电组合模型，该模型可转化为确定性的半定规划问题，并且易于通过成熟求解器求解。所提出的模型与求解办法为供电公司的购电决策提供了新方法，可有效增强供电公司的风险管理能力。

1 分布不确定的条件风险

1.1 风险与条件风险

风险价值VaR（value-at-risk）［15］不满足一致性公理，缺乏次可加性，计算形式上等同于机会约束规划；CVaR模型在避免直接求解机会约束规划的同时弥补了VaR缺乏对尾部损失测量的不足。

1.2 确定分布下的条件风险

设决策变量x∈X，随机变量y∈Rm，并且定义f（x，y）∈R为损失函数，其中，X为满足一定条件的投资组合可行集，X∈Rn，y表示如收益率等的随机因素。假设y的概率分布函数已知，则y有联合概率密度函数p（y），固定x，损失函数 f（x，y）关于随机因素不超过损失临界值α的概率为

当置信水平为β∈（0，1）时，VaR和CVaR可分别表示为

由于CVaR表达式中含有VaR函数项，而VaR的表达式难以用显式表达，文献［16］中引入一个相对简单的函数代替VaR来求解CVaR，即

式中，［f（x，y）-α］+表示max（0，f（x，y）-α）。式（4）为关于α的凸函数，并且连续可微。文献［17］已经证明：

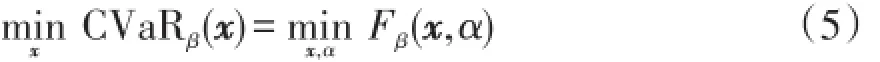
1.3 分布鲁棒条件风险

考虑到很难获取现实中准确的概率分布，而随机变量的部分信息（如期望和方差）相对容易获取。另外，如果将具有相同期望和方差的所有可能概率分布下的最大条件风险价值用来描述供电公司购电组合投资所面对的风险，将有效提高购电组合方案的鲁棒性，增强供电公司规避风险的能力。

对应式（4）和（5），可以将分布鲁棒的条件风险描述［18］为

式中：P为随机向量y的联合概率分布；集合Γ包含满足相同期望值向量μ和协方差矩阵Σ的所有可能联合概率分布，P∈Γ。考虑Γ包含所有可能的概率分布，则最大条件风险表示为，计算形式为式（6）等号右边内容。

供电公司可以通过最小化式（6）中的最大条件风险，进而获得鲁棒性更强的购电组合方案。

1.4 分布鲁棒条件风险对偶转换

分布鲁棒条件风险方法是一种将随机规划与鲁棒优化相结合的方法［19］。考虑在给定期望和方差的条件下，优化对决策结果影响最严重分布下的CVaR值。由于式（6）右边代表分布鲁棒效果的只有期望值部分，故只给出分布鲁棒期望值的对偶转换即可。

在分布不确定情况下，优化关于函数Φ（x， y）的最大期望可表示为

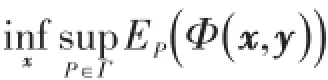
直接求解上述问题时，该问题是一个NP困难问题。文献［18］提出通过对偶原理将上述问题转换为半无限规划问题，同时其满足强对偶条件。则的对偶半无限规划问题为

式中：M∈R（m+1）（m+1）为对称矩阵；tr代表迹运算；

当Φ（x， y）为关于y的一次或二次函数，可以通过Farkas Lemma或S-lemma将对偶后的半无限规划问题转换为半定规划SDP（semi-definite program⁃ming）问题进行求解。

2 供电公司购电组合模型

2.1 基本假设

假设终端价格接受政府管制，在不同市场电价均值基础上增加固定收益率部分［5］。

令xT=［x1x2…xm］∈X为供电公司购电组合向量，其中，X为购电组合可行集，xi（i= 1，2，…，m）代表供电公司在不同市场中的购电比例，满足（ ）。又令yii=1，2，…，m 表示供电公司在不同市场中的买入价，多元随机变量yT=［y1y2…ym］表示市场电价组合向量，则购电组合成本为

记实时交易市场、日前交易市场、中长期合约市场中的电价y的均值为，方差为。本文假设不同市场中电价概率分布不确定，采用符合相同均值μ与方差σ2的所有可能概率分布下的最大风险作为约束，参数b为固定收益率，则面向客户的固定零售电价向量为

2.2 建立模型

根据上文中的假设，单位组合收益可表示为

单位损失函数表示为

单位组合期望收益表示为

式（6）可通过式（7）进行求解得

进而采用分布鲁棒条件风险价值来计算损失函数 f（x，y）对应的风险值，以R（x）最大为目标函数，在分布鲁棒条件风险价值约束下，供电公司组合收益最大的优化模型为

式中，ω为供电公司所能接受的风险上限，且ω≥0。

3 仿真计算

3.1 算例分析

通过某电力市场100天内在实时、日前和中长期合约市场的购电价格数据y=［ ］y1y2y3，得到3个市场的购电价均值和方差，表1为各市场购电价格数据。取各售电市场零售电价为wi=（1+b）E（yi），b=0.1，并在Matlab平台上利用半定规划求解器SDPT3［20］求解优化模型（12）得到相关结果见表2，其中的xi（i=1，2，3）代表供电公司在实时、日前和中长期合约市场的购电量比例，ω值与最后一列的DRCVaR相同，因而没有列出。

为观察购电组合期望收益R（x，y）随DRCVaR值变化的曲线，改变ω所代表的风险上限，重复计算最大期望收益的值，进而得到如图1所示的均值-DRCVaR有效前沿曲线，可见满足约束的最优组合都在有效前沿上。

由图1可知，当设置风险参数β为不同值时，均值-DRCVaR的有效前沿也不相同。实际决策过

表1 各市场购电电价Tab.1 Electricity price in different markets $/（MW·h）

表2 购电量分配结果及DRCVaR值Tab.2 Allocation of power purchases and DRCVaR

图1 均值-DRCVaR有效前沿Fig.1 Efficient frontier of mean-DRCVaR

程中，所设置的ω值存在下限，不能任意小，否则求解模型（12）时会出现无有效解的情况；而增大ω值时，虽然不会导致模型无解，但当达到一定上限后，期望收益R（x）不再随ω值增大而增加，原因是组合策略x=［ ］1 0 0不再改变，此时对应期望收益的极值为5.33。图1中的1、2两点代表不同风险下组合收益-鲁棒条件风险的极大值点，在此基础上增大ω收益不再增加；1′和2′点代表不同风险下组合收益-鲁棒条件风险的极小值点，在此基础上减小ω模型不再有解。

3.2 算例结果鲁棒性分析

表1中的仿真数据来自文献［11］，选用相同的仿真数据为了便于将本文结论与上述文献中假设3个市场中电价均满足正态分布的仿真结果做比较。与文献［11］相比，本文所提的分布鲁棒条件风险价值对风险的约束性更强，具体表现在当β取值固定时，在相同的期望收益下，本文结论中的分布鲁棒条件风险价值相比基于正态分布的CVaR值更小，中长期市场分配量更大，说明本文的结论保守性更强。

4 结语

本文所提的模型针对的是不同市场电价满足相同期望和方差情况下的所有可能概率分布，理论上要比基于某一种概率分布下得到的结果更为保守，但是这必要的保守性可以换来供电公司风险管理上的可靠性，丰富了供电公司在电力市场运行中的思维方式和经营方法。

参考文献：

［1］孔祥玉，杨群，穆云飞，等（Kong Xiangyu，Yang Qun，Mu Yunfei，et al）.分时电价环境下用户负荷需求响应分析方法（Analysis method for customers demand response in time of using price）［J］.电力系统及其自动化学报（Pro⁃ceedings of the CSU-EPSA），2015，27（10）：75-80．

［2］张富强，周浩（Zhang Fuqiang，Zhou Hao）.电力市场中的电价分布问题（Probability distribution of prices in elec⁃tricity market）［J］.电力系统自动化（Automation of Elec⁃tric Power Systems），2006，30（4）：22-28．

［3］白利超，康重庆，夏清，等（Bai Lichao，Kang Chongqing，Xia Qing，et al）.不确定性电价分析（Analysis on the un⁃certainty of electricity price）［J］.中国电机工程学报（Pro⁃ceedings of the CSEE），2002，22（5）：36-41．

［4］ 罗凤章，肖峻，王成山，等（Luo Fengzhang，Xiao Jun，Wang Chengshan，et al）.计及电价波动的电网建设项目经济评估区间法（An interval economic evaluation meth⁃od for projects of power system planning considering elec⁃tricity price fluctuation）［J］.电网技术（Power System Technology），2005，29（8）：20-24．

［5］刘皓明，韩蜜蜜，侯云鹤，等（Liu Haoming，Han Mimi，Hou Yunhe，et al）.供电公司多能量市场最优购电组合的加权CVaR模型（A mean-weighted CVaR model for distribution company’s optimal portfolio in multi-energy markets）［J］.电网技术（Power System Technology），2010，34（9）：133-138.

［6］冯冬涵，甘德强，钟金，等（Feng Donghan，Gan Deqiang，Zhong Jin，et al）.发电商多交易策略的有效前沿分析（一）模型的建立（An efficient frontier analysis for the GenCo multi trading strategy part one model analysis）［J］.电力系统自动化（Automation of Electric Power Sys⁃tems），2007，31（13）：29-35．

［7］冯冬涵，甘德强，钟金，等（Feng Donghan，Gan Deqiang，Zhong Jin，et al）.发电商多交易策略的有效前沿分析（二）算法的实现（An efficient frontier analysis for the GenCo multi trading strategy part two algorithm design）［J］.电力系统自动化（Automation of Electric Power Sys⁃tems），2007，31（14）：31-37，42．

［8］郭金伟，周渝慧（Guo Jinwei，Zhou Yuhui）.电力市场条件下供电公司最优购电问题研究（Optimized electricity purchase for power supply companies in electricity mar⁃kets）［J］.华东电力（East China Electric Power），2008，36 （1）：64-66．

［9］陈晓林，刘俊勇，宋永华，等（Chen Xiaolin，Liu Junyong，Song Yonghua，et al）.利用差价合同和金融输电权的组合规避电力市场风险（Use of CFDS and FTRS to hedge against risks of power market）［J］.中国电机工程学报（Proceedings of the CSEE），2005，25（10）：75-81．

［10］郭金，江伟，谭忠富（Guo Jin，Jiang Wei，Tan Zhongfu）.风险条件下供电公司最优购电问题研究（Research on optimized power purchasing of power suppliers under risk condition）［J］.电网技术（Power System Technology），2004，28（11）：18-22．

［11］王壬，尚金成，周晓阳，等（Wang Ren，Shang Jincheng，Zhou Xiaoyang，et al）.基于条件风险价值的购电组合优化及风险管理（Conditional value at risk based optimiza⁃tion of power purchasing portfolio in multiple electricity markets and risk management）［J］.电网技术（Power Sys⁃tem Technology），2006，30（20）：72-76．

［12］李春华，王钦，文福拴（Li Chunhua，Wang Qin，Wen Fushuan）.基于机会约束规划的供电公司最优购电策略（Chance-constrained programming based approach to optimal purchasing strategies of distribution companies）［J］.电力系统及其自动化学报（Proceedings of the CSUEPSA），2007，19（6）：12-17．

［13］王金凤，李渝曾，张少华（Wang Jinfeng，Li Yuzeng，Zhang Shaohua）.基于CVaR的供电公司电能购买决策模型（CVaR-based electricity purchase model for power supply company）［J］.电力自动化设备（Electric Power Automation Equipment），2008，28（2）：19-23．

［14］王壬，尚金成，冯旸，等（Wang Ren，Shang Jincheng，Feng Yang，et al）.基于CVaR风险计量指标的发电商投标组合策略及模型（Combined bidding strategy and model for power suppliers based on CVaR risk measure⁃ment techniques）［J］.电力系统自动化（Automation ofElectric Power Systems），2005，29（14）：5-9．

［15］朱文昊，谢品杰（Zhu Wenhao，Xie Pinjie）.基于CVaR的峰谷分时电价对供电公司购电组合策略影响分析（Influence analysis of CVaR model based TOU electricity price on portfolio strategy）［J］.电力系统保护与控制（Power System Protection and Control），2015，43（14）：16-21.

［16］Rockafellar R T，Uryasev S.Optimization of conditional value-at-risk［J］.Journal of Risk，1999，29（1）：1071-1074.

［17］周任军，姚龙华，童小娇，等（Zhou Renjun，Yao Long⁃hua，Tong Xiaojiao，et al）.采用条件风险方法的含风电系统安全经济调度（Security economic dispatch in wind power integrated systems using a conditional risk method）［J］.中国电机工程学报（Proceedings of the CSEE），2012，32（1）：56-63.

［18］Zymler Steve，Kuhn Daniel，Rustem Berc.Distributionally robust joint chance constraints with second-order moment information［J］.Mathematical Programming，2013，137（1-2）：167-198.

［19］周任军，闵雄帮，童小娇，等（Zhou Renjun，Min Xiong⁃bang，Tong Xiaojiao，et al）.电力环保经济调度矩不确定分布鲁棒优化方法（Distributional robust optimization under moment uncertainty of environmental and economic dispatch for power system）［J］.中国电机工程学报（Pro⁃ceedings of the CSEE），2015，35（13）：3248-3256.

［20］Tutuncu R H，Toh K C，Todd M J.Solving semidefinitequadratic-linear programs using SDPT3［J］.Mathematical Programming，2003，95（2）：189-217.

中图分类号：TM73

文献标志码：A

文章编号：1003-8930（2016）07-0130-05

DOI：10.3969/j.issn.1003-8930.2016.07.024

作者简介：

夏海杰（1993—），男，本科，研究方向为电力系统规划、电力市场。Email：476896608@qq.com

林士勇（1978—），男，通讯作者，硕士，工程师，研究方向为电力营销管理。Email：58105979@qq.com

收稿日期：2016-01-20；修回日期：2016-04-20

Electricity Purchasing Portfolio Strategies for Distribution Companies Considering Distributional Robust CVaR

XIA Haijie1，LIN Shiyong2
（1.College of Physical and Electronic Engineering，Taizhou University，Taizhou 318000，China；2.Zhejiang Yueqing Power Supply Company，Yueqing 325600，China）

Abstract：Considering the uncertainty of probability distribution of electricity price in multi-energy markets and on the premise of guaranteeing distributional robust conditional value-at-risk constraint is satisfied，taking the expected profits maximization as a target，this paper establishes the optimal power purchasing model.A case study of purchasing propor⁃tion in real-time electricity market，day-ahead electricity market，and mid-long term contract market is transformed into a semi-definite programming problem.The analysis shows the efficiency of the proposed model，which presents a new way for distribution company to determine the optimal purchasing strategies considering the risk.

Key words：distributional robust；conditional value-at-risk（CVaR）；semi-definite programming（SDP）；electricity purchasing portfolio strategy